En esta página, estudiamos el movimiento de una espira cuadrada superconductora, de lado a y masa m que se mueve en el plano horizontal en el seno de un campo magnético no homogéneo perpendicular al plano tal como se muestra en la figura

${\displaystyle \overrightarrow{B}\{\begin{array}{l}{B}_0\widehat{k},x<0\\ B_0\left(1+kx\right)\widehat{k},x\ge 0\end{array}}$

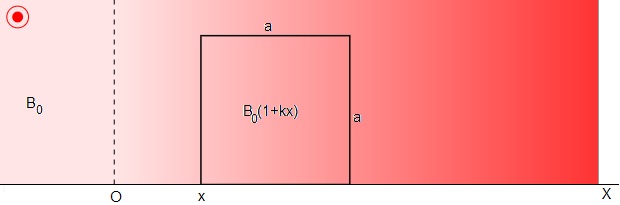
El campo magnético es constante para x<0, y se incrementa linealmente con x para x≥0.

Movimiento para x≥0

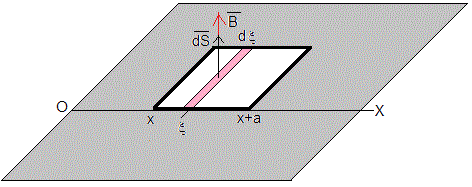
El flujo total Φ a través de la espira es la suma del flujo producido por el campo magnético externo

${\displaystyle \begin{array}{l}{\Phi }_e={\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}={{\displaystyle \underset{x}{\overset{x+a}{\int }}{B}_0(1+k\xi )(a·d\xi )·\cos 0=B_{0}a\left(\xi +\frac{k}{2}{\xi }^2\right)|}}_x^{x+a}\\ =B_0{a}^2\left(1+\frac{k}{2}a+kx\right)\end{array}}$

y el flujo propio, Φ_a=Li. Donde L es el coeficiente de autoinducción y i es la intensidad que circula por la espira

Intensidad de la corriente en la espira

${\displaystyle iR=-\frac{d\Phi }{dt}=-\frac{d({\Phi }_e+{\Phi }_a)}{dt}=-B_0{a}^{2}k\frac{dx}{dt}-L\frac{di}{dt}}$

Si la resistencia es nula, R=0

${\displaystyle \begin{array}{l}-B_0{a}^{2}k\frac{dx}{dt}-L\frac{di}{dt}=0\\ i=-\frac{B_0{a}^{2}k}{L}x\end{array}}$

Hemos supuesto que intensidad es nula, i=0 cuando la espira parte del origen x=0.

El flujo aumenta, el sentido de la corriente inducida es el de las agujas del reloj.

Obtenemos esta misma expresión, suponiendo que el flujo a través de la espira Φ_e+Φ_a es constante e igual al flujo inicial

${\displaystyle \begin{array}{l}\Phi =B_0{a}^2\left(1+\frac{k}{2}a+kx\right)+Li=B_0{a}^2\left(1+\frac{k}{2}a\right)\\ i=-\frac{B_{0}k{a}^2}{L}x\end{array}}$

Ecuación del movimiento

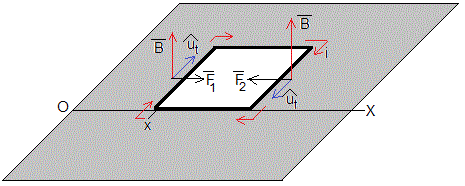
El campo magnético ejerce una fuerza sobre los lados de la espira, $\overrightarrow{F}=i({\widehat{u}}_t\times \overrightarrow{B})L$. La fuerza que ejerce el campo magnético sobre los lados horizontales de la espira son perpendiculares a dichos lados y no influyen en el movimiento horizontal de la espira.

• La fuerza F₂ que ejerce el campo magnético sobre el lado derecho de la espira, cuya posición es x+a apunta hacia la izquierda

${\displaystyle F_2=i{B}_0\left(1+k(x+a)\right)a}$

• La fuerza F₁ que ejerce el campo magnético sobre el lado izquierdo de la espira cuya posición es x, apunta hacia la derecha y es menor que F₂

${\displaystyle F_1=i{B}_0\left(1+kx\right)a}$

La fuerza neta está dirigida hacia la izquierda, es proporcional al desplazamiento x y de sentido contrario al mismo

${\displaystyle F_1-F_2=-i{B}_{0}k{a}^2=-\frac{B_0^2{k}^2{a}^4}{L}x}$

La ecuación diferencial de este Movimiento Armónico Simple es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\frac{B_0^2{k}^2{a}^4}{L}x\\ \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=\mathrm{0,}{\omega }^2=\frac{B_0^2{k}^2{a}^4}{mL}\end{array}}$

La solución de esta ecuación diferencial es conocida,

${\displaystyle \begin{array}{l}x=A\cos (\omega t)+B\sin (\omega t)\\ \frac{dx}{dt}=\omega \left(-A\sin (\omega t)+B\cos (\omega t)\right)\end{array}}$

Si la espira parte de la posición x=0, con velocidad v₀

${\displaystyle x=\frac{v_0}{\omega }\sin (\omega t)}$

El máximo desplazamiento de la espira es v₀/ω. El tiempo que tarda en regresar al origen es medio periodo

${\displaystyle P=\frac{\pi }{\omega }=\frac{\pi }{B_{0}k{a}^2}\sqrt{mL}}$

El movimiento no depende del valor del campo magnético B₀ estático, sino del gradiente B₀k, es decir, cómo se incrementa el campo magnético con x

Energías

En el instante t=0, la intensidad de la corriente que circula por la espira es i=0, su velocidad v=v₀, la energía de la espira de masa m es cinética

${\displaystyle E_i=\frac{1}{2}m{v}_0^2}$

En el instante t, la espira se encuentra en la posición x, la intensidad de la corriente y su velocidad son

${\displaystyle \begin{array}{l}\{\begin{array}{l}i=\frac{B_0{a}^{2}k}{L}x=\frac{B_0{a}^{2}k}{L}\frac{v_0}{\omega }\sin (\omega t)=v_0\sqrt{\frac{m}{L}}\sin (\omega t)\\ v=v_0\cos (\omega t)\end{array}\\ E_f=\frac{1}{2}m{v}^2+\frac{1}{2}L{i}^2=\frac{1}{2}m{v}_0^2\end{array}}$

La energía total permanece constante

Movimiento en el intervalo -a<x<0

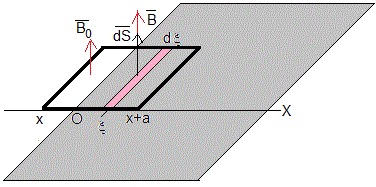
Cuando la posición x de la espira (lado izquierdo) está comprendida -a<x<0. El flujo a través de la espira se compone de tres términos

• El flujo del campo magnético B₀(1+kx) a través de la parte de la espira comprendida entre 0 y x+a

${\displaystyle \begin{array}{l}{\Phi }_1={\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}={{\displaystyle \underset{0}{\overset{x+a}{\int }}{B}_0(1+k\xi )(a·d\xi )·\cos 0=B_{0}a\left(\xi +\frac{k}{2}{\xi }^2\right)|}}_0^{x+a}=\\ B_{0}a\left((x+a)+\frac{k}{2}{\left(x+a\right)}^2\right)\end{array}}$

• El flujo del campo magnético constante, B₀ a través de la parte de la espira comprendida entre x y 0

${\displaystyle {\Phi }_2=B_{0}a(-x)=-B_{0}ax}$

• El flujo propio, Φ₃=Li. Donde L es el coeficiente de autoinducción y i es la intensidad que circula por la espira

Intensidad de la corriente en la espira

Como la resistencia de la espira es nula, R=0, el flujo total a través de la espira es constante e igual al inicial

${\displaystyle \begin{array}{l}{B}_{0}a\left((x+a)+\frac{k}{2}{\left(x+a\right)}^2\right)-B_{0}ax+Li=B_{0}a\left(a+\frac{k}{2}{a}^2\right)\\ i=-B_{0}ka\frac{\left(\frac{1}{2}x+a\right)x}{L}\end{array}}$

Como -a<x<0, i>0. El flujo disminuye, el sentido de la corriente inducida es el contrario a las agujas del reloj.

Ecuación del movimiento

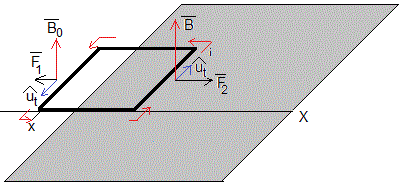
• La fuerza F₂ que ejerce el campo magnético sobre el lado derecho de la espira, cuya posición es x+a, apunta hacia la derecha

${\displaystyle F_2=i{B}_0\left(1+k(x+a)\right)a}$

• La fuerza F₁ que ejerce el campo magnético sobre el lado izquierdo de la espira cuya posición es x, apunta hacia la izquierda y es menor que F₂

${\displaystyle F_1=i{B}_{0}a}$

La fuerza neta F₂-F₁ está dirigida hacia la derecha, de sentido contrario al desplazamiento x (hacia la izquierda). La ecuación diferencial ya no es un Movimiento Armónico Simple

${\displaystyle \frac{d^{2}x}{d{t}^2}=-B_0^2{k}^2{a}^2\frac{\left(\frac{1}{2}x+a\right)\left(x+a\right)x}{mL}}$

Se resuleve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=P (medio periodo) x=0, dx/dt=-v₀

Cuando x=-a, la espira se introduce completamente en la región de campo magnético constante.

Movimiento en el intervalo x<-a

• El flujo del campo magnético a través de la espira, B₀a²
• El flujo propio, Li

Intensidad de la corriente en la espira

La suma es igual al flujo inicial

${\displaystyle \begin{array}{l}{B}_0{a}^2+Li=B_{0}a\left(a+\frac{k}{2}{a}^2\right)\\ i=\frac{B_{0}k}{2L}{a}^3\end{array}}$

Ecuación del movimiento

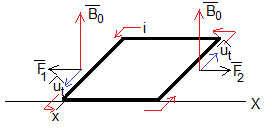
La fuerza sobre la espira es cero, F₁=F₂ y de sentido contrario. La espira se mueve con velocidad constante, la velocidad al final de la segunda etapa del movimiento

Calculamos esta velocidad aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2=\frac{1}{2}L{i}^2+\frac{1}{2}m{v}^2\\ v=\sqrt{v_0^2-\frac{1}{4}\frac{B_0^2{k}^2{a}^6}{mL}}\end{array}}$

Movimiento completo

Consideremos el siguiente ejemplo:

• Lado de la espira, a=40 cm
• Velocidad inicial, v₀=3 m/s
• Campo magnético, producto B₀k=0.01 T/m
• Masa de la espira, m=11.22 g
• Autoinducción, L=1.89·10^-6 H

Posición de la espira en función del tiempo

a=0.4; %lado de la espira
v0=3; %velocidad inicial	
B0=0.01; %campo magnético, producto B_0·k
densidad=8.93; %cobre
r=1/2000; %radio del cable
m=4*a*pi*r*r*densidad*1000; %masa
L=8e-7*a*(log(a/r)-0.7740); %autoinducción

w=B0*a^2/sqrt(m*L); %frecuencia angular
hold on
fplot(@(t) v0*sin(w*t)/w,[0,pi/w])
f=@(t,x) [x(2); -B0*B0*a^2*(a+x(1)/2)*(x(1)+a)*x(1)/(m*L)]; 
opts=odeset('events',@(t,x) stop_superconductor(t,x,a));
[t,x]=ode45(f,[0,pi/w],[0,-v0],opts);
plot(t+pi/w, x(:,1))
line([t(end)+pi/w,t(end)+pi/w+0.1],[x(end,1), x(end,1)+x(end,2)*0.1])
hold off
grid on
xlabel('t')
ylabel('x')
title('Espira superconductora. Posición')

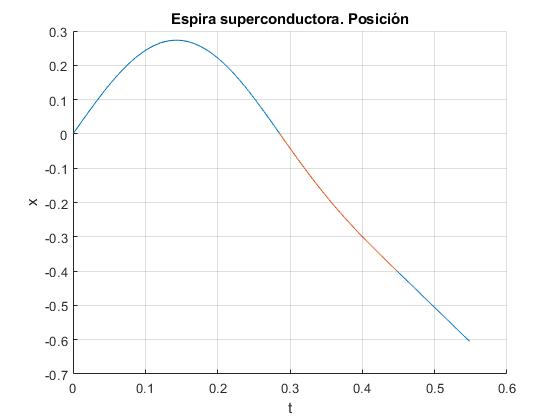
Para describir la segunda etapa del movimiento, -a<x<0, resolvemos la ecuación diferencial por procedimientos numéricos y detenemos el proceso cuando la espira alcanza la posición x=-a. Para ello definimos la función

function [value,isterminal,direction]=stop_superconductor(t,x, a)
    value=x(1)+a;  
    isterminal=1;
    direction=-1; 
end

Velocidad de la espira en función de la posición

v0=3; %velocidad inicial	
B0=0.01; %campo magnético, producto B_0·k
densidad=8.93; %cobre
r=1/2000; %radio del cable
m=4*a*pi*r*r*densidad*1000; %masa
L=8e-7*a*(log(a/r)-0.7740); %autoinducción

w=B0*a^2/sqrt(m*L); %frecuencia angular
hold on
fplot(@(t) v0*sin(w*t)/w, @(t) v0*cos(w*t), [0,pi/w])
f=@(t,x) [x(2); -B0*B0*a^2*(a+x(1)/2)*(x(1)+a)*x(1)/(m*L)]; 
opts=odeset('events',@(t,x) stop_superconductor(t,x,a));
[t,x]=ode45(f,[0,pi/w],[0,-v0],opts);
plot(x(:,1),x(:,2))
vFin=sqrt(v0^2-B0^2*a^6/(4*m*L));
line([-a-0.1,-a],[-vFin, -vFin])
hold off
grid on
xlabel('x')
ylabel('v')
title('Espira superconductora. Velocidad')

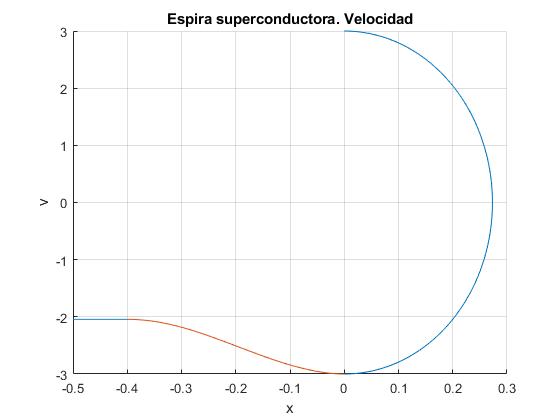
La velocidad inicial es v₀ para x=0, medio periodo después, la velocidad es -v₀ para x=0. Para x<-a, la velocidad se mantiene constante. Comprobamos que la velocidad al terminar la segunda etapa, coincide con la calculada aplicando el principio de conservación de la energía

>> vFin,x(end,2)
vFin =    2.0434
ans =   -2.0434

Intensidad de la corriente en la espira en función de la posición

a=0.4; %lado de la espira
v0=3; %velocidad inicial	
B0=0.01; %campo magnético, producto B_0·k
densidad=8.93; %cobre 8g/cm3)
r=1/2000; %radio del cable
m=4*a*pi*r*r*densidad*1000; %masa
L=8e-7*a*(log(a/r)-0.7740); %autoinducción

hold on
line([0,a],[0,-B0*a^3/L])
line([a,0],[-B0*a^3/L,0])
fplot(@(x) -B0*a*(a+x/2).*x/L,[-a,0],'r')
line([-a-0.1,-a],[B0*a^3/(2*L), B0*a^3/(2*L)])
hold off
grid on
xlabel('x')
ylabel('i')
title('Espira superconductora. Intensidad')

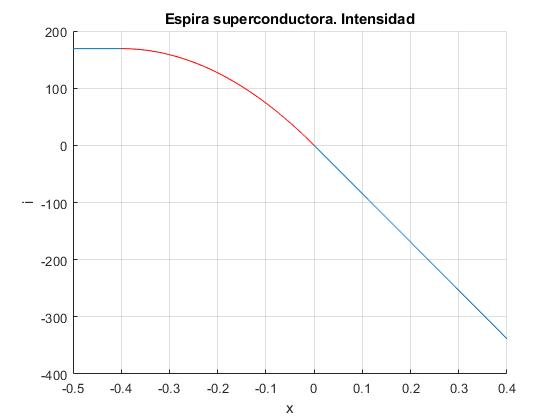
La intensidad inicial es nula en x=0, disminuye y vuelve a aumentar linealmente con x hasta volver a ser nula cuando la espira regresa al origen, x=0, luego aumenta en el intervalo -a<x<0, hasta que se hace constante cuando la espira se mueve en el campo homogéneo, x<-a

Actividades

Se introduce

• La densidad ρ del material conductor del cable con el que está fabricada la espira cuadrada, en el control titulado Densidad
• La velocidad inicial de la espira, v₀ en x=0, en el control titulado Velocidad
• El producto B₀k, en el contro titulado Campo magnético

El programa interactivo ha fijado los valores de los siguientes parámetros:

• El lado de la espira, a=40 cm, y el radio del cable 2r=1 mm. El coeficiente de autoinducción se calcula mediante la siguiente fórmula aproximada

${\displaystyle L=\frac{{\mu }_0}{\pi }2a\left\{\log \left(\frac{a}{r}\right)-\text{0}\text{.7740}\right\}}$

La masa del cable con el que se ha fabricado la espira, m=ρ(πr²)·(4a)

En la parte superior, se proporcionan los datos del tiempo t en s, la posición x del extremo izquierdo de la espira, su velocidad v en m/s, y la intensidad de la corriente que circula por la espira

Los puntos de color rojo sobre la espira representan portadores de carga positivos y señalan el sentido de la corriente inducida en la espira. Estos puntos se mueven con una velocidad proporcional a la intensidad de la corriente.

• Primero, observamos el movimiento oscilatorio de la espira durante medio periodo.
• En la segunda etapa del movimiento, la espira va saliendo del campo no homogéneo y va entrando en el homogéneo
• En la tercera, la espira se mueve con velocidad constante en el campo homogéneo. La intensidad de la corriente en el espira no cambia

Referencias

Physics Challenge for Teachers and Students. Solution to April 2008 Challenge. The Physics Teacher, Vol 46, 2008