Centro de masas
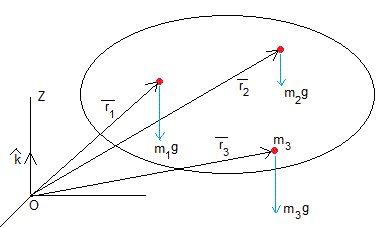
Consideremos un sistema formado por varias partículas, m1, m2, m3... que está situado en el campo gravitatorio terrestre, que podemos considerar uniforme y paralelo al eje vertical Z, si el sistema no es muy extenso. Las fuerza que ejerce sobre cada una de las partículas (su peso) es
La resultante de las fuerzas (el peso total es)
siendo n el número de partículas.
Las posiciones de las partículas respecto del Sistema de Referencia OXYZ son . El momento total del sistema de fuerzas paralelas respecto del origen O es
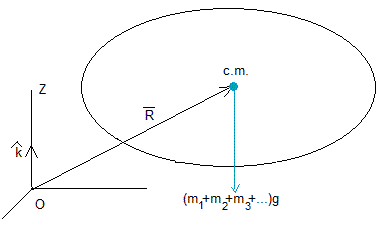
El centro de masas (c.m.) del sistema de partículas se define como un punto geométrico cuya posición es , donde situamos la resultante del sistema de fuerzas paralelas (el peso total).
Para determinar la posición del centro de masas, igualamos el momento de la resultante al momento total del sistema de fuerzas paralelas.
Las coordendas xc, yc, zc del centro de masas son
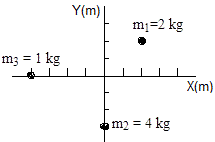
Ejemplo
Determinar la posición del centro de masas del sistema de partículas de la figura
- La posición de la masa m1=2 kg es
- La posición de la masa m2=4 kg es
- La posición de la masa m3=1 kg es
Centro de masas y simetría
En un polígono regular, en un círculo, en una esfera, etc., el centro de masas se sitúa en su centro de simetría.
En un cono, en una pirámide, etc., el centro de masa se sitúa en su eje de simetría, más cerca de la base que del vértice.
Ejemplo
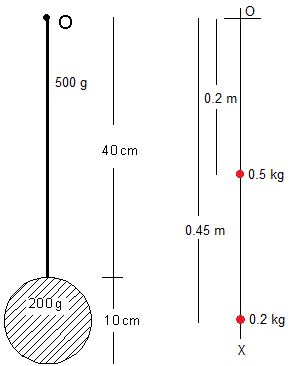
El péndulo de un reloj está formado por una varilla de 500 g y 40 cm de longitud y una lenteja en forma cilíndrica de 200 g de masa y 5 cm de radio, tal como se indica en la figura. Determinar la posición de su centro de masa respecto del extremo O.
Sustituímos la varilla por una masa puntual de 0.5 kg situado a 0.2 cm del extremo O y la lenteja por una masa puntual situada a 0.45 m de O
El centro de masas del sistema formado por las dos partículas es
27 cm por debajo del extremo O de la varilla
Centro de masas de un sólido de forma cónica, de radio R y altura h
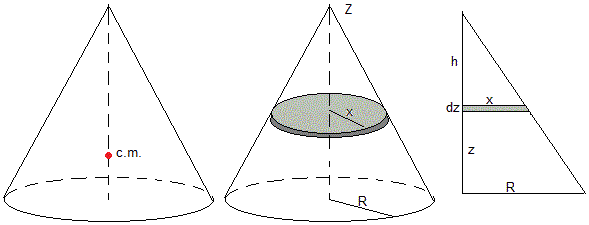
Por simetría el centro de masas estará situado en el eje Z del cono a una altura zc de la base. Estará más cerca de la base que del vértice
Dividimos el cono en cilindros de radio x y de altura dz tal como se muestra en la figura. La masa de cada uno de los cilindros es dm=ρ·πx2dz. Siendo ρ la densidad del sólido homogéneo
Dado que la posición del centro de masas de este cilindro de masa dm es z. El centro de masas zc del cono es
La posición del centro de masas es independiente de la densidad ρ del sólido homogéneo
Para evaluar la integral del numerador y del denominador, relacionamos el radio x con el radio R del cono y su altura h
- la integral del numerador vale πR2·h2/12
- la integral del denominador vale πR2·h/3 (volumen del cono)
La posición del centro de masas del cono zc=h/4
Centro de masas de una figura plana homogénea
Determinar la posición del centro de masa de la figura plana y homogénea formada por un rectángulo y un cuarto de círculo.
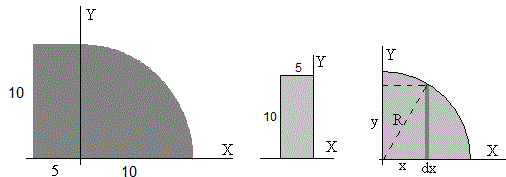
Centro de masa del rectángulo de área 50, x1=-2.5, y1=5
Centro de masa del cuarto de círculo de área π·102/4=25π.
El eje de simetría es la bisetriz del primer cuadrante x2=y2
Calculamos x2 o y2. Elemento diferencial de área, dA=y·dx
Para calcular el área del cuarto de círculo, se ha efectuado el cambio de variable, x=R·cosθ, dx=-R·sinθ.
Centro de masas de las dos figuras
Recipente cilíndrico parcialmente lleno de líquido
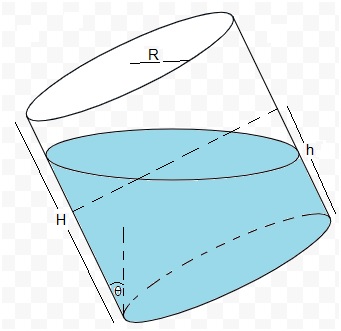
Un recipiente cilíndrico de radio R y altura H contiene un líquido de densidad ρ hasta una altura h. El recipiente se inclina un ángulo θ respecto de la vertical. Vamos a calcular la posición del centro de masa del sistema formado por el líquido y el recipiente que lo contiene.
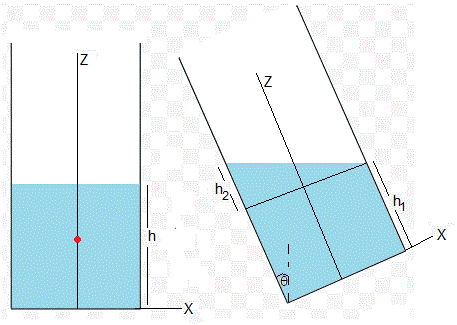
Un punto de color rojo, a una altura h/2, señala la posición del centro de masas del líquido cuando el recipiente está en la posición inicial, θ=0
Cuando se inclina el recipiente un ángulo θ, el ángulo está limitado ya que h1+h2<H, para que el líquido no se derrame. En los cálculos de la posición del c.m. se tiene en cuenta que h1≥0
Cuando el recipiente se inclina un ángulo θ, el volumen de líquido πR2h no cambia, pero lo hace el centro de masas del líquido. Estableceremos un sistema de referencia XZ inclinado como se señala en la figura. El eje Z es el eje del recipiente cilíndrico
Coordenada xl del centro de masa del líquido
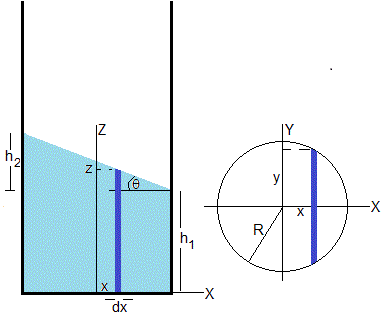
Volumen de líquido
Dividimos el líquido en elementos infinitesimales paralelos al eje Z de volumen dV=(2y·dx)z, en color azul oscuro en la figura
Calcularemos el volumen del líquido con el fin de relacionar la altura h1 con h
La segunda integral es inmediata. Para resolver la primera integral, hacemos el cambio de variable, x=Rcosφ, dx=-Rsinφ·dφ
La relación entre h y h1 es
Del mismo modo tendremos que
Coordenada xl
La primera integral es nula, como hemos mostrado anteriormente. Calculamos la segunda, haciendo el cambio de variable, x=Rcosφ, dx=-Rsinφ·dφ
La coordenada xl del centro de masas del líquido es
Coordenada zl del centro de masa del líquido
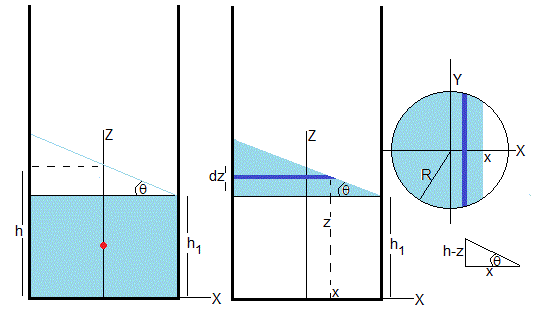
Calculamos la coordenada zl del centro de masa del líquido, como suma de dos porciones
El volumen de la porción inferior es V1=πR2h1 y su centro de masa se encuentra en h1/2
La coordenada zl del centro de masa del líquido es
Hemos dividido, la porción superior en elementos infinitesimales de espesor dz y de área de la base A(z), en color azul claro en la parte derecha de la figura
Haciendo el cambio de variable, x=Rcosφ, dx=-Rsinφ·dφ
donde la relación entre z y x es, h-z=xtanθ, Véase la parte inferior derecha de la figura
Volumen de la porción superior
Primero, comprobamos que la suma de los volúmenes de las dos porciones es el volumen total del líquido contenido en el recipiente cilíndrico, V1+V2=πR2h, o bien, πR2h1+V2=πR2h.
Hacemos el cambio de variable
Calculamos V2
Integramos el arccos(), por partes, la tercera es inmediata
El resultado es
Comprobación
Coordenada zl del centro de masa del líquido
La primera integral multiplicada por h la hemos resuelta en el apartado anterior. Resolvemos la segunda multiplicada por -tanθ que a su vez es la suma de tres integrales, la primera es inmediata
El resultado de z2 es
Combinamos las dos porciones para obtener la coordenada zl del c.m. del líquido
Centro de masas del recipiente y del líquido que contiene
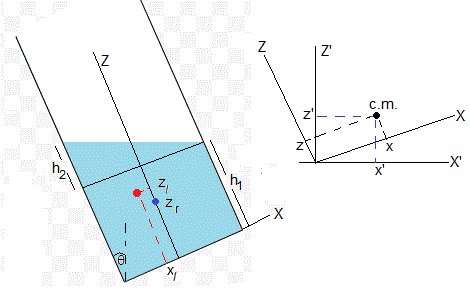
El centro de masas del recipiente de masa mr está, por simetría, en el eje Z (0,zr), el centro de masas del recipiente y del líquido que contiene es
La masa del líquido es ml=ρ(πR2h) , ρ es la densidad
Angulo crítico
La posición del centro de masas del recipiente y del líquido que contiene xcm y zcm en el sistema de referencia girado XZ un ángulo θ. En el sistema de referencia horizontal y vertical X'Z', la posición del centro de msas se obtiene mediante la transformación
La posición del centro de masas está en la vertical Z', por encima del punto de apoyo, si x'=0, para el ángulo θ denominado crítico
Calculamos el ángulo crítico θ0
Buscamos la raíz real de la ecuación de tercer gardo
La raíz real, véase el apartado Fórmulas para calcular las raíces, de una ecuación cúbica
Hay una raíz real si R2>Q3, lo que se cumple, que vale
Representamos el ángulo crítico θ0 en grados, en función del parámetro α manteniendo fijos los parámetros β=0.28 y γ=3.5
function cm_botella
beta=0.28; %parámetros
gamma=3.5;
aa=linspace(0.5,6,100);
angulo=zeros(1, length(aa));
k=1;
for alfa=aa
b=4*alfa^2+8*beta*gamma+2;
c=8*(alfa+beta);
raiz=raices_3([1,0,b,-c]);
angulo(k)=atan(raiz(1))*180/pi; %ángulo en grados
k=k+1;
end
plot(aa,angulo)
grid on
xlabel('\alpha')
ylabel('\theta_0')
title('Equilibro inestable')
function x = raices_3(p)
Q=(p(2)*p(2)-3*p(3))/9;
R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
x=zeros(3,1); %reserva memoria para un vector de tres elementos
if (R*R)<(Q^3)
tetha=acos(R/sqrt(Q^3));
x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
else
A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
if A==0
B=0;
else
B=Q/A;
end
x(1)=(A+B)-p(2)/3;
x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
end
end
end
La función
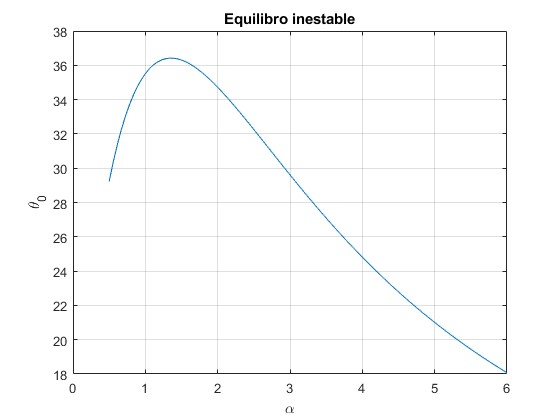
Alternativamente, determinamos explícitamente la raíz real de la ecuación cúbica
beta=0.28; %parámetros
gamma=3.5;
alfa=linspace(0.5,6,100);
b=4*alfa.^2+8*beta*gamma+2;
c=8*(alfa+beta);
Q=-b/3;
R=c/2;
A=-(-R+sqrt(R.^2-Q.^3)).^(1/3);
angulos=atan(A+Q./A);
plot(alfa,angulos*180/pi)
grid on
xlabel('\alpha')
ylabel('\theta_0')
title('Equilibro inestable')
Referencias
Andrew Davis Cahoon. Water Bottle Stability. The Physics Teacher, Vol. 61, December 2023. pp. 785-787

