Fuerza electromotriz inducida
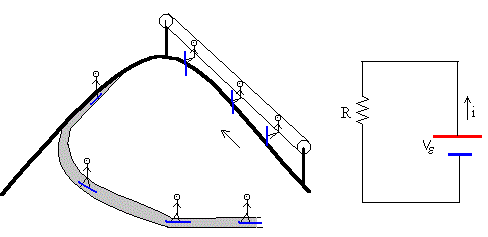
En una pista de esquí, los remontes mecánicos suben a los esquiadores hasta el alto de una colina, después, los esquiadores bajan deslizando pendiente abajo. Los esquiadores son equivalentes a los portadores de carga, el remonte mecánico incrementa la energía potencial del esquiador. Luego, el esquiador baja deslizándose por la colina hasta la base del remonte.
En un conductor los portadores de carga (positivos) se mueven espontáneamente desde un lugar en el que el potencial es más alto hacia otro lugar en el que el potencial es más bajo, es decir, en la dirección del campo eléctrico. Para mantener el estado estacionario es necesario proveer de un mecanismo que transporte los portadores de carga desde un potencial más bajo hasta un potencial más elevado.
El generador de Van de Graaff es un ejemplo de este mecanismo. Las cargas positivas se mueven en dirección contraria al campo eléctrico, en el que el potencial aumenta y las negativas en la misma dirección que el campo, en el que el potencial disminuye. La fuerza o la energía necesaria para este transporte de cargas lo realiza el motor que "bombea" las cargas.
Se denomina fuerza electromotriz o fem Vε al trabajo por unidad de carga que realiza el dispositivo. Aunque la unidad de la fem es la misma que la de una diferencia de potencial, se trata de conceptos completamente diferentes. Una fem produce una diferencia de potencial pero surge de fenómenos físicos cuya naturaleza no es necesariamente eléctrica (en el generador de Van de Graaff es mecánica, en una pila es de naturaleza química, en la varilla que estudiamos en esta página es magnética, etc. ).
Una fem es un trabajo por unidad de carga, este trabajo no lo realiza necesariamente una fuerza conservativa, mientras que la diferencia de potencial es el trabajo por unidad de carga realizado por una fuerza eléctrica que es conservativa.
Fuerza sobre los portadores de carga
Vamos a obtener la fem por otro procedimiento distinto, examinando las fuerzas sobre los portadores de carga positivos existentes en la varilla.
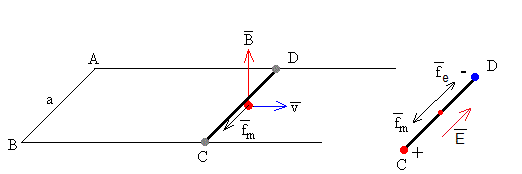
Al moverse la varilla hacia la derecha, con velocidad en el seno de un campo magnético uniforme , los portadores de carga se mueven con la misma velocidad horizontal. La fuerza sobre dichos portadores es
Como y son perpendiculares, el módulo de la fuerza es
fm=qvB
La dirección de la fuerza magnética es la de la varilla y el sentido de D a C. El extremo C se carga con carga positiva y el extremo D con carga negativa. A medida que se va acumulando la carga, se va estableciendo un campo eléctrico E que va de C a D. Este campo ejerce una fuerza sobre los portadores de carga qE. Se deja de acumular carga en los extremos cuando la fuerza eléctrica fe se compensa con la magnética fm, es decir, cuando E=vB
La diferencia de potencial entre C y D es el producto del campo eléctrico constante E=vB por la distancia a entre ambos extremos, VC-VD=vBa.
El área barrida por la varilla en un dt es: a·dx; como B es constante, la rapidez de cambio del flujo magnético será:
siendo v la velocidad que lleva la varilla.
Actividades
Se introduce:
- El campo magnético. Inicialmente el campo magnético apunta en la dirección vertical, hacia el lector (color rosa). Si introducimos un valor negativo, se cambia el sentido del campo magnético (color azul claro).
- La velocidad de la varilla.
- La longitud del conductor.
Los puntos de color rojo en un extremo de la varilla indican carga positiva y los de color azul en el otro extremo, carga negativa.
Se pulsa el botón titulado Nuevo.
Se activa la casilla Fuerza para ver las fuerzas sobre los portadores de carga (positivos)
Observamos el área barrida por la varilla, en color amarillo
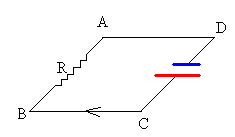
Como hemos visto C está a un potencial mayor que D. Al conectar C y D mediante las guías, la corriente fluye espontáneamente de C a D pasando por B y A.
Tenemos el equivalente a una batería que produce una fem Vε=vBa. Si la resistencia del circuito es R, la intensidad de la corriente inducida es
Actividades
Se introduce:
- El campo magnético. Inicialmente el campo magnético apunta en la dirección vertical, hacia el lector (color rosa). Si introducimos un valor negativo, se cambia el sentido del campo magnético (color azul claro).
- La velocidad de la varilla.
- La longitud del conductor.
Se pulsa el botón titulado Nuevo.
Se activa la casilla Fuerza para ver la fuerza que impulsa los portadores de carga (positivos)
Movimiento circular de una varilla

Sea una varilla de longitud a, su extremo O está fijo y su extremo P describe un movimiento circular con velocidad angular constante ω
Consideremos un portador de carga positivo situado a una distancia x de O, describe un circunferencia de radio x con velocidad constante v=ωx. La fuerza que ejerce el campo magnético sobre dicho portador de carga es fm=qBωx
El extremo P de la varilla se carga positivamente y el extremo O negativamente, se establece un campo eléctrico que va de P a O. Se deja de acumular carga cuando la fuerza que ejerce el campo eléctrico fe=qE se compense con la fuerza que ejerce el campo magnético fm, es decir, cuando E=Bωx
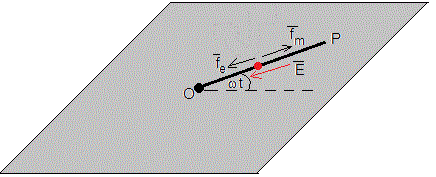
Dado que el campo eléctrico E depende de x, para calcular diferencia de potencial entre P y O hay que integrar
Para calcular la f.e.m., utilizando la ley de Faraday, hallaremos la variación del flujo magnético a través del área barrida por la varilla cuando ésta gira. Obsérvese que, en este caso, la forma geométrica de esa área es un sector circular (recordamos que el área de un sector circular, inscrito en un círculo de radio: a y con un ángulo de apertura: θ vale: S=θa2/2. Dado que se trata de un movimiento circular uniforme, θ=ωt
Finalmente, mencionaremos que la fórmula que calcula la fem que se produce en un circuito en movimiento en el seno de un campo magnético es
Actividades
Se introduce:
- El campo magnético. Inicialmente el campo magnético apunta en la dirección vertical, hacia el lector (color rosa). Si introducimos un valor negativo, se cambia el sentido del campo magnético (color azul claro).
- La velocidad angular de la varilla.
- La longitud del conductor.
Los puntos de color rojo en un extremo de la varilla indican carga positiva y los de color azul en el otro extremo, carga negativa.
Se pulsa el botón titulado Nuevo.
Se activa la casilla Fuerza para ver las fuerzas sobre los portadores de carga (positivos)
Observamos el área barrida por la varilla, en color amarillo
Referencias
Los programas interactivos han sido creados en colaboración con José Manuel Almudí y Mikel Ceberio, profesores de la E.U.I.T.I. de Bilbao (Universidad del País Vasco)

