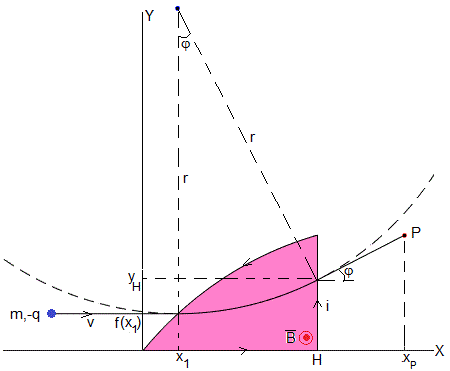
La forma de la sección del solenoide se representa mediante una línea negra cuyo interior es de color rosa. Consta de tres segmentos, una línea horizontal de longitud H en la parte inferior, otra vertical en la parte derecha y la función y=f(x) a determinar a la izquierda.

La intensidad de la corriente que recorre el solenoide se indica mediante flechas en la figura, el campo magnético es perpendicular al plano de la espira y apunta hacia el lector de acuerdo con la regla de la mano derecha

Para representar parte de la figura, se ha empleado el código

yp=0.5;
xp=1.5;
H=1;
r=1.75;

f=@(x) yp-r+sqrt(r^2-(H-x).^2)-(H-x)*(xp-H)./sqrt(r^2-(H-x).^2);
xx=linspace(0,H,50);
yy=f(xx);
hold on
fill([xx,H,H],[yy,f(H),f(0)],[1 0.5 0.8])

x=0.2;
y=f(x);
line([-0.5,x],[y,y],'color','k')
phi=asin((H-x)/r);
fplot(@(t) x+r*sin(t), @(t) y-r*cos(t)+r,[0,phi], 'k')
fplot(@(t) x+r*sin(t), @(t) y-r*cos(t)+r,[-phi-pi/24,phi+pi/6], 'k', 
'lineStyle','--')
plot(x,y+r,'bo','markersize',3,'markerfacecolor','b')
y_H=y+r-sqrt(r^2-(H-x)^2);
m=(H-x)/sqrt(r^2-(H-x)^2);
g=@(x) m*(x-H)+y_H;
fplot(g,[H,xp],'k')
plot(xp,yp,'ro','markersize',3,'markerfacecolor','r') %centro
hold off
% xlim([0,1.5])
xlabel('x')
ylabel('y')
title('Lente magnética')
axis equal

Cuando la partícula de masa m y carga q entra en el solenoide en la posición x₁, f( x₁) expriementa una fuerza $\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}$, que la hace describir un movimiento circular uniforme de radio r

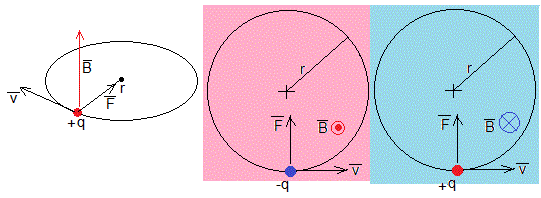
Aplicando la dinámica del movimiento circular uniforme

${\displaystyle \begin{array}{l}qvB=m\frac{v^2}{r}\\ r=\frac{mv}{qB}\end{array}}$

La partícula sale del solenoide en la posición (H, y_H) con la misma velocidad siguiendo una línea recta tangente a la circunferencia en dicho punto y llega al punto (x_P, y_P). Con estos datos, vamos a determinar la función y=f(x).

La ecuación de la circunferencia de radio r y centro en (x₁, r+f(x₁)) es

${\displaystyle \begin{array}{l}{\left(x-x_1\right)}^2+{\left(y-f\left(x_1\right)-r\right)}^2=r^2\\ y=f\left(x_1\right)+r\pm \sqrt{r^2-{\left(x-x_1\right)}^2}\end{array}}$

con 0<x₁<H

La carga abandona el solenoide en la posición (H, y_H) que es el otro extremo del arco de circunferencia de radio r

${\displaystyle \begin{array}{l}{\left(H-x_1\right)}^2+{\left(y_H-f\left(x_1\right)-r\right)}^2=r^2\\ y_H=f\left(x_1\right)+r\pm \sqrt{r^2-{\left(H-x_1\right)}^2}\end{array}}$

Como y_H<f(x₁)+r, elegimos la solución con el signo negativo

${\displaystyle y_H=f\left(x_1\right)+r-\sqrt{r^2-{\left(H-x_1\right)}^2}}$

Cuando deja el solenoide la partícula se mueve a lo largo de una línea recta tangente a la circunferencia en el punto (H, y_H), la pendiente es

${\displaystyle m={\left(\frac{dy}{dx}\right)}_{x=H}=\frac{H-x_1}{\sqrt{r^2-{\left(H-x_1\right)}^2}}}$

Alternativamente, el ángulo φ del arco de circunferencia es

${\displaystyle \begin{array}{l}\sin \phi =\frac{H-x_1}{r}\\ m=\tan \phi =\frac{\sin \phi }{\sqrt{1-{\sin }^2\phi }}=\frac{\frac{H-x_1}{r}}{\sqrt{1-\frac{{\left(H-x_1\right)}^2}{r^2}}}=\frac{H-x_1}{\sqrt{r^2-{\left(H-x_1\right)}^2}}\end{array}}$

La ecuación de la línea recta es

${\displaystyle y=y_H+m\left(x-H\right),x>H}$

Sabiendo que esta recta pasa por el punto P (x_P, y_P) despejamos f(x₁)

${\displaystyle \begin{array}{l}{y}_P=y_H+m\left(x_P-H\right)=y_H+\frac{\left(H-x_1\right)\left(x_P-H\right)}{\sqrt{r^2-{\left(H-x_1\right)}^2}}\\ y_P=f\left(x_1\right)+r-\sqrt{r^2-{\left(H-x_1\right)}^2}+\frac{\left(H-x_1\right)\left(x_P-H\right)}{\sqrt{r^2-{\left(H-x_1\right)}^2}}\\ f\left(x_1\right)=y_P-r+\sqrt{r^2-{\left(H-x_1\right)}^2}-\frac{\left(H-x_1\right)\left(x_P-H\right)}{\sqrt{r^2-{\left(H-x_1\right)}^2}}\end{array}}$

0<x₁<H es la abscisa genérica x del segmento horizontal, luego la función f(x) buscada es

${\displaystyle y=f\left(x\right)=y_P-r+\sqrt{r^2-{\left(H-x\right)}^2}-\frac{\left(H-x\right)\left(x_P-H\right)}{\sqrt{r^2-{\left(H-x\right)}^2}}}$

Las partículas tienen carga negativa, el campo magnético apunta hacia el lector

yp=0.5; %foco
xp=1.5;
H=1;
r=1.75; %radio

f=@(x) yp-r+sqrt(r^2-(H-x).^2)-(H-x)*(xp-H)./sqrt(r^2-(H-x).^2);
xx=linspace(0,H,50);
yy=f(xx);
hold on
fill([xx,H,H],[yy,f(H),f(0)],[1 0.5 0.8])

for x=[0.15,0.35, 0.65]
    y=f(x);
    line([0,x],[y,y],'color','k')
    phi=asin((H-x)/r);
    fplot(@(t) x+r*sin(t), @(t) y-r*cos(t)+r,[0,phi], 'k')
    y_H=y+r-sqrt(r^2-(H-x)^2);
     m=(H-x)/sqrt(r^2-(H-x)^2);
    g=@(x) m*(x-H)+y_H;
    fplot(g,[H,xp],'k')
end
plot(xp,yp,'ro','markersize',3,'markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
title('Lente magnética')
axis equal

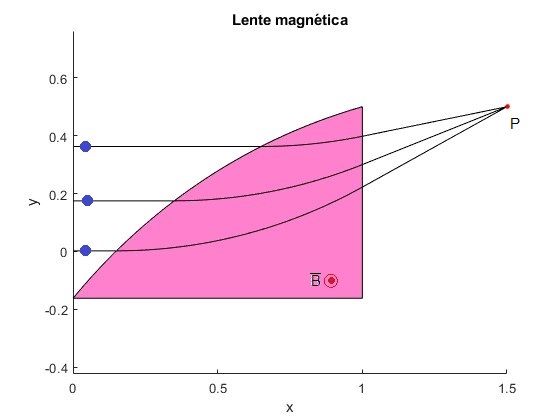
Las partículas tienen carga positiva, el campo magnético apunta hacia el lector

yp=0.5; %foco
xp=1.5;
H=1;
r=1.75; %radio

f=@(x) yp-r+sqrt(r^2-(H-x).^2)-(H-x)*(xp-H)./sqrt(r^2-(H-x).^2);
xx=linspace(0,H,50);
yy=f(xx);
hold on
fill([xx,H,H],[yy,f(H),f(0)],[1 0.5 0.8])

for x=[0.2,0.45, 0.65]
    y=f(x);
    line([0,x],[y,y],'color','k')
    phi=asin((H-x)/r);
    fplot(@(t) x+r*sin(t), @(t) y+r*cos(t)-r,[0,phi], 'k')
    y_H=y-r+sqrt(r^2-(H-x)^2);
    m=(H-x)/sqrt(r^2-(H-x)^2);
    g=@(x) -m*(x-H)+y_H;
    fplot(g,[H,xp],'k')
end
plot(xp,yp,'ro','markersize',3,'markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
title('Lente magnética')
axis equal

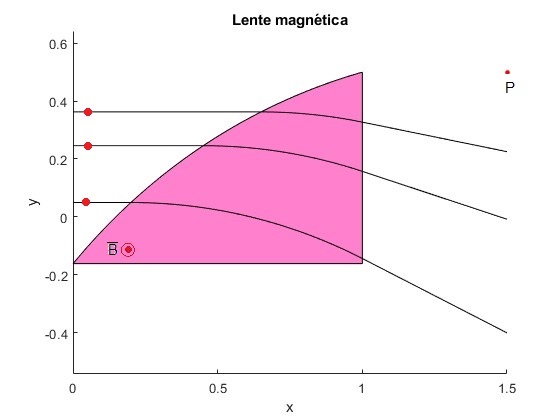
Para obtener las mismas trayectorias para las partículas que tienen carga positiva, el campo magnético apunta en sentido contrario (la corriente en el solenoide cambia de sentido)

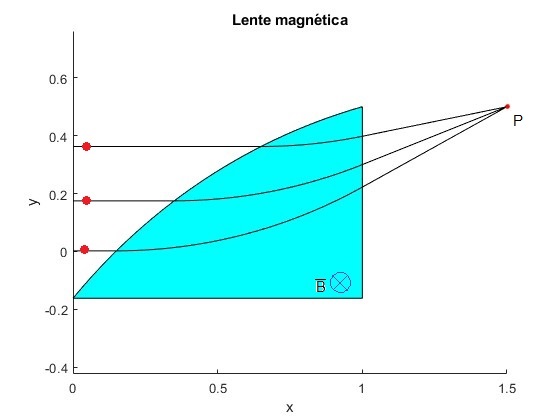
Espectrómetro de masas

Los iones de distinta masa (isótopos) con la misma velocidad, describen trayectorias circulares de radios distintos en el seno de un campo magnético constante

yp=0.5; %foco
xp=1.5;
H=1;
r=1.75;

f=@(x) yp-r+sqrt(r^2-(H-x).^2)-(H-x)*(xp-H)./sqrt(r^2-(H-x).^2);
xx=linspace(0,H,50);
yy=f(xx);
hold on
fill([xx,H,H],[yy,f(H),f(0)],[0 1 1])

x=0.2;
for r=[1.75, 1.5,1] %radios de las trayectorias circulares
    y=f(x);
    line([-0.5,x],[y,y],'color','k')
    phi=asin((H-x)/r);
    fplot(@(t) x+r*sin(t), @(t) y-r*cos(t)+r,[0,phi], 'k')
    y_H=y+r-sqrt(r^2-(H-x)^2);
    m=(H-x)/sqrt(r^2-(H-x)^2);
    g=@(x) m*(x-H)+y_H;
    fplot(g,[H,xp],'k')
end
plot(xp,yp,'ro','markersize',3,'markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
title('Lente magnética')
axis equal

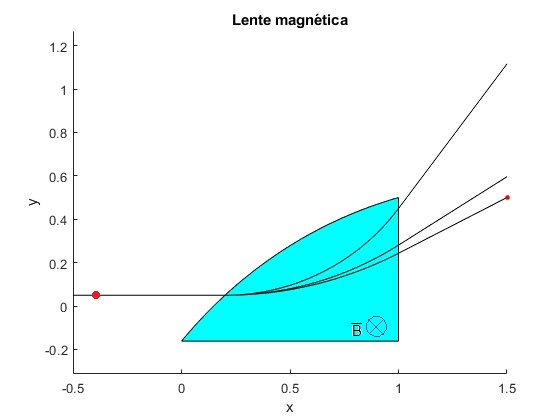
Un ión de masa m describe un arco de circunferencia de radio r, a continuación, una trayectoria rectilínea que llega al punto P

${\displaystyle r=\frac{mv}{qB}}$

Para que otro ión de masa m' llegue al mismo punto P se cambia el campo magnético de B a B' de modo que el radio r sea el mismo

${\displaystyle r=\frac{m\text{'}v}{qB\text{'}}}$

El cambio del campo magnético en el interior del solenoide es tan sencillo como modificar la corriente i que lo recorre

Conocida la masa m del ión obtenemos la masa m' de otro isótopo mediante la relación

${\displaystyle \frac{m\text{'}}{B\text{'}}=\frac{m}{B}}$

El campo magnético en el interior de un solenoide es constante e igual a B=μ₀ni, n es el número de espiras por unidad de longitud. La relación entre masas es

${\displaystyle \frac{m\text{'}}{m}=\frac{i\text{'}}{i}}$

Referencias

Ardi Khalifah, Riri Murniati, Mikrajuddin Abdullah. Magnetic Lens Made of a Single Solenoid for Controlling Bending of Two-Dimensional Ion Beam. https://arxiv.org/pdf/2302.08319