Los polos magnéticos existen en pares, polo norte y polo sur. Cuando rompemos un imán aparecen dos imanes cada uno con un par de polos opuestos.

Aunque no se ha encontrado, la existencia del monopolo fue propuesta por el físico Paul Dirac

En reposo, el monopolo de carga q_m crea un campo magnético estático, similar al campo eléctrico creado por una carga eléctrica q. El campo $\overrightarrow{B}$ en un punto P cuyo vector posición es $\overrightarrow{r}$ con origen en el monopolo es

${\displaystyle \overrightarrow{B}=k_m\frac{q_m}{r^2}\widehat{r}}$

k_m es la constante de proporcionalidad que determinaremos más adelante en el Sistema Internacional de Unidades de Medida

La unidad de carga magnética

La fuerza que ejerce un campo magnético sobre un monopolo de carga q_m es

${\displaystyle \overrightarrow{F}=q_m\overrightarrow{B}}$

En cambio, la fuerza que ejerce un campo magnético sobre una carga eléctrica en movimiento es

${\displaystyle \overrightarrow{F}=q\left(\overrightarrow{v}\times \overrightarrow{B}\right)}$

Comparando ambas fórmulas, vemos que las unidades de q_m son las unidades de q·v (carga por velocidad), Cm/s=A·m. También podemos compararla con la fórmula de la fuerza que ejerce un campo magnético sobre una porción de corriente rectilínea

${\displaystyle \overrightarrow{F}=i\left(\widehat{u_t}\times \overrightarrow{B}\right)l}$

Las unidades de q_m son las de i·l (intensidad por longitud), es decir, A·m

La constante de proporcionalidad, k_m.

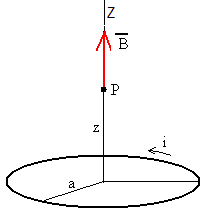
El campo magnético producido por una espira circular en un punto de su eje es

${\displaystyle B=\frac{{\mu }_{0}i{a}^2}{2{\left(z^2+a^2\right)}^{3/2}}}$

Un monopolo de carga q_m está situado en el punto P, la fuerza que experimenta es

${\displaystyle F_z=q_m\frac{{\mu }_{0}i{a}^2}{2{\left(z^2+a^2\right)}^{3/2}}}$

Por otra parte, el monopolo ejerce una fuerza igual y de sentido contario sobre la espira circular

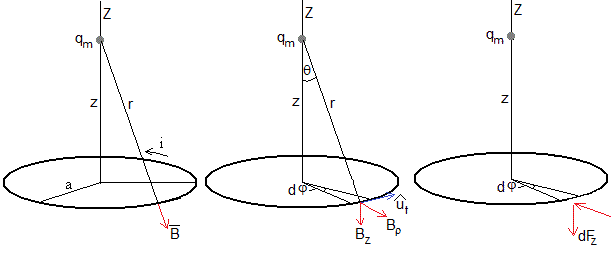
El campo magnético producido por el monopolo en un punto de la espira es

${\displaystyle B=k_m\frac{q_m}{r^2}=k_m\frac{q_m}{a^2+z^2}}$

que tiene dos componentes, una radial B_ρ y otro a lo largo del eje Z, B_z

La componente B_z, ejerce una fuerza en la dirección radial que no afecta a la espira supuesta rígida. La componente radial B_ρ ejerce una fuerza en la dirección del eje Z, sentido negativo (hacia abajo), que vamos a calcular

${\displaystyle B_{\rho }=k_m\frac{q_m}{r^2}\sin \theta =k_m\frac{q_{m}a}{{\left(a^2+z^2\right)}^{3/2}}}$

La fuerza que ejerce la componente radial B_ρ, sobre la porción ds=a·dφ de corriente es

${\displaystyle d{F}_z=-i{B}_{\rho }ds=-k_m\frac{q_{m}i{a}^2}{{\left(a^2+z^2\right)}^{3/2}}d\phi }$

La resultante es

${\displaystyle F_z=-k_m\frac{q_{m}i{a}^2}{{\left(a^2+z^2\right)}^{3/2}}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\phi }=-2\pi k_m\frac{q_{m}i{a}^2}{{\left(a^2+z^2\right)}^{3/2}}}$

La tercera ley de Newton implica que

${\displaystyle \begin{array}{l}\frac{{\mu }_0}{2}=2\pi k_m\\ k_m=\frac{{\mu }_0}{4\pi }\end{array}}$

Campo eléctrico producido por un monopolo en movimiento

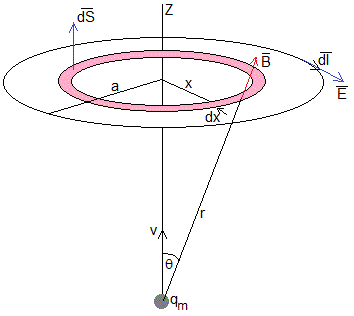
Las cargas eléctricas en movimiento (corriente) producen un campo magnético. Del mismo modo, un monopolo en movimiento produce un campo eléctrico de acuerdo con la ley de Faraday.

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}}$

Una variación en el tiempo del flujo del campo magnético produce una fem, V_ε, una corriente inducida que se opone a las variaciones de flujo (ley de Lenz). En el caso de que no haya un conductor, se produce un campo eléctrico cuya circulación es la fem V_ε

Supongamos que el monopolo se mueve a lo largo del eje Z con velocidad constante v. Consideremos una circunferencia de radio a centrada en el eje Z. El flujo a través de la superficie circular de radio a es

${\displaystyle \begin{array}{l}\Phi ={\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}={\displaystyle \underset{0}{\overset{a}{\int }}\left(\frac{{\mu }_0}{4\pi }\frac{q_m}{r^2}\right)\left(2\pi x·dx\right)\cos \theta }={\displaystyle \underset{0}{\overset{a}{\int }}\left(\frac{{\mu }_0}{4\pi }\frac{q_m}{z^2+x^2}\right)\left(2\pi x·dx\right)\frac{-z}{\sqrt{z^2+x^2}}}=\\ -\frac{{\mu }_0{q}_m}{2}z{\displaystyle \underset{0}{\overset{a}{\int }}\frac{x·dx}{{\left(z^2+x^2\right)}^{3/2}}}=\frac{{\mu }_0{q}_m}{2}z\left(\frac{1}{\sqrt{z^2+a^2}}-\frac{1}{-z}\right)=\frac{{\mu }_0{q}_m}{2}\left(\frac{z}{\sqrt{z^2+a^2}}+1\right)\end{array}}$

Calculamos la fem V_ε

${\displaystyle V_{\epsilon }=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=-\frac{{\mu }_0{q}_m}{2}\frac{\sqrt{z^2+a^2}-\frac{z^2}{\sqrt{z^2+a^2}}}{z^2+a^2}\frac{dz}{dt}=-\frac{{\mu }_0{q}_m}{2}\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}v}$

El flujo aumenta, el sentido del campo eléctrico es el que se muestra en la figura. Por simetría, el campo eléctrico es constante y tangente a la circunferencia de radio a

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}=E·2\pi a\\ E·2\pi a=-\frac{{\mu }_0{q}_m}{2}\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}v\\ E=-\frac{{\mu }_0{q}_m}{4\pi }\frac{a}{{\left(z^2+a^2\right)}^{3/2}}v=-\frac{{\mu }_0{q}_m}{4\pi }\frac{v\sin \theta }{r^2}\end{array}}$

Denominamos E_m al campo eléctrico producido por el monopolo en movimiento. El vector $\overrightarrow{E_m}$, se puede expresar como producto vectorial, ya que es perpendicuar al plano determinado por el vector velocidad, $\overrightarrow{v}$ y al vector posición, $\overrightarrow{r}$, tal como se aprecia en la figura

${\displaystyle \overrightarrow{E_m}=-\frac{{\mu }_0{q}_m}{4\pi }\frac{\overrightarrow{v}\times \widehat{r}}{r^2}}$.

Comparación

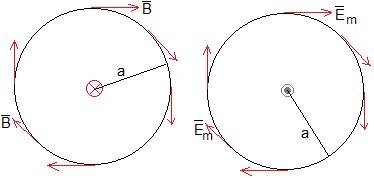
Una corriente rectilínea indefinida perpendicular al plano de la pantalla hacia dentro, produce un campo magnético a una distancia a

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi a}}$

en el sentido indicado en la parte izquierda de la figura (regla de la mano derecha)

Un monopolo que se mueve perpendicular al plano de la pantalla, hacia afuera, produce un campo eléctrico, tal como se indica en la parte derecha de la figura.

Interacción entre un monopolo y una corriente rectilínea

Vamos a mostrar, que como resultado de la interacción, el monopolo incrementa su energía cinética a costa de la disminución de la intensidad (velocidad de los portadores de carga) de la corriente rectilínea

Campo eléctrico producido por el monopolo en movimiento circular uniforme

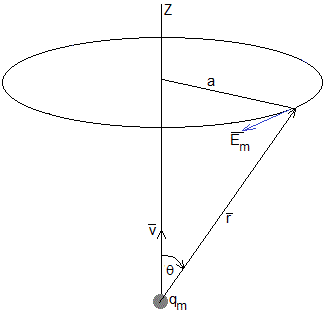
En la figura de la izquierda, se muestra una carga magnética q_m que se mueve con velocidad constante v en una trayectoria circular de radio a. Calculamos el campo eléctrico producido por la carga magnética en movimiento. El problema es similar al cálculo del campo magnético producido por una corriente circular en un punto de su eje Z

El campo eléctrico $\overrightarrow{E_m}$ es perpendicular al plano determinado por el vector $\overrightarrow{v}$ y el vector unitario $\widehat{r}$. El sentido es el indicado en la figura. Su módulo es

${\displaystyle E_m=\frac{{\mu }_0{q}_m}{4\pi }\frac{v}{z^2+a^2}}$

La componente de dicho campo a lo largo del eje Z es

${\displaystyle E_z=-E_m\cos \left(90-\theta \right)=-E_m\sin \theta =-\frac{{\mu }_0{q}_m}{4\pi }\frac{v}{z^2+a^2}\frac{a}{\sqrt{z^2+a^2}}=-\frac{{\mu }_0{q}_m}{4\pi }\frac{va}{{\left(z^2+a^2\right)}^{3/2}}}$

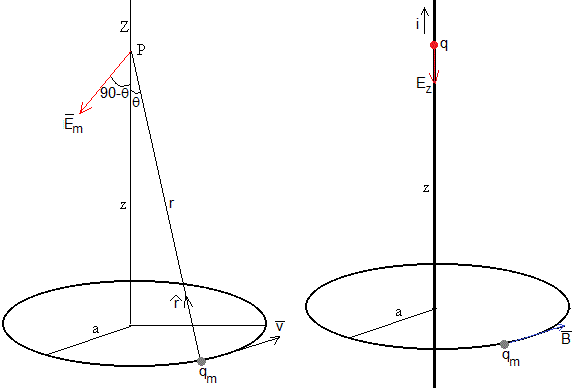
Supongamos que existe una corriente eléctrica rectilínea indefinida de intensidad i a lo largo del eje Z, parte derecha de la figura

Fuerza sobre los portadores de carga

La componente E_z del campo eléctrico es opuesto al movimiento de los portadores de carga. La energía por unidad de tiempo P es

${\displaystyle P=i{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\overrightarrow{E}·dz\widehat{k}=}i{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{E}_{z}dz=-}i\frac{{\mu }_0{q}_{m}va}{4\pi }{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dz}{{\left(z^2+a^2\right)}^{3/2}}}}$

Para resolver esta integral se hace el cambio, z=atant, dz=a·dt/cos²t

${\displaystyle {\displaystyle \int \frac{dz}{{\left(z^2+a^2\right)}^{3/2}}}={\displaystyle \int \frac{a\frac{dt}{{\cos }^{2}t}}{a^3\frac{1}{{\cos }^{3}t}}}=\frac{1}{a^2}{\displaystyle \int \cos t·dt}=\frac{1}{a^2}\sin t}$

Deshacemos los cambios, teniendo en cuenta la relación trigonométrica

${\displaystyle \sin t=\frac{\tan t}{\sqrt{1+{\tan }^{2}t}}=\frac{\frac{z}{a}}{\sqrt{1+\frac{z^2}{a^2}}}=\frac{z}{\sqrt{z^2+a^2}}}$

El resultado es

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dz}{{\left(z^2+a^2\right)}^{3/2}}}={\frac{1}{a^2}\frac{z}{\sqrt{z^2+a^2}}|}_{-\infty }^{\infty }=\frac{2}{a^2}}$

La energía por unidad de tiempo P es

${\displaystyle P=-\frac{{\mu }_{0}i{q}_{m}va}{4\pi }\frac{2}{a^2}=-\frac{{\mu }_{0}i{q}_m}{2\pi a}v=-\frac{{\mu }_{0}i{q}_m}{\tau }}$

Donde τ es el tiempo que tarda el monopolo en dar una vuelta completa. El trabajo durante este tiempo es

${\displaystyle W=P·\tau =-q_m{\mu }_{0}i}$

Campo magnético producido por la corriente rectilínea y fuerza sobre el monopolo

Por otra parte, el campo magnético producido por el hilo rectilíneo ejerce una fuerza $\overrightarrow{F}=q_m\overrightarrow{B}$ sobre la carga magnética.

${\displaystyle W={\displaystyle \oint \overrightarrow{F}·\overrightarrow{dl}}=q_m{\displaystyle \oint \overrightarrow{B}·\overrightarrow{dl}}}$

Aplicamos la ley de Ampère

${\displaystyle W=q_m{\mu }_{0}i}$

El trabajo de esta fuerza se invierte en incrementar la energía cinética del monopolo

La carga del monopolo, q_m

Supongamos que una carga eléctrica q describe una trayectoria circular de radio a, con velocidad angular ω₀. El campo eléctrico producido por el monopolo en movimiento a lo largo del eje Z con velocidad v, aumentará o disminuirá la velocidad angular de dicha carga.

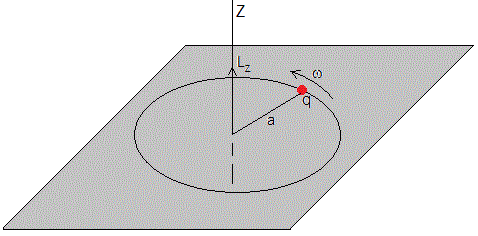
El campo eléctrico produce una fuerza qE sobre la carga y un momento qE·a, que cambia la componente Z del momento angular, L_z

${\displaystyle \begin{array}{l}\frac{d{L}_z}{dt}=qEa\\ \frac{d{L}_z}{dt}=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}v\\ d{L}_z=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}v·dt=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}dz\end{array}}$

Integramos respecto de la variable z entre -∞ y +∞

${\displaystyle L_z=\frac{{\mu }_{0}q{q}_m}{4\pi }{a}^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dz}{{\left(z^2+a^2\right)}^{3/2}}}}$

Se ha obtenido el resultado de esta integral en el apartado anterior

La componente Z del momento angular, L_z, vale

${\displaystyle \begin{array}{l}{L}_z=\frac{{\mu }_{0}q{q}_m}{4\pi }{a}^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dz}{{\left(z^2+a^2\right)}^{3/2}}}=-\frac{{\mu }_{0}q{q}_m}{4\pi }{a}^2{\frac{1}{a^2}\frac{z}{\sqrt{z^2+a^2}}|}_{-\infty }^{\infty }=-\frac{{\mu }_{0}q{q}_m}{4\pi }-\frac{{\mu }_{0}q{q}_m}{4\pi }\\ L_z=-\frac{{\mu }_{0}q{q}_m}{2\pi }\end{array}}$

De otra forma, que evita resolver la integral, es la siguiente

${\displaystyle \begin{array}{l}\frac{d{L}_z}{dt}=qEa\\ \frac{d{L}_z}{dt}=q\frac{V_{\epsilon }}{2\pi a}a\\ \frac{d{L}_z}{dt}=-\frac{q}{2\pi }\frac{d\Phi }{dt}\\ \Delta L_z=-\frac{q}{2\pi }\Delta \Phi \end{array}}$

La variación de flujo entre z=-∞ y z=+∞

${\displaystyle \begin{array}{l}\Phi =\frac{{\mu }_0{q}_m}{2}\left(\frac{z}{\sqrt{z^2+a^2}}+1\right)\\ \Delta \Phi =\Phi (\infty )-\Phi (-\infty )={\mu }_0{q}_m-0={\mu }_0{q}_m\\ \Delta L_z=-\frac{{\mu }_{0}q{q}_m}{2\pi }\end{array}}$

La regla de cuantización de Bohr dice que el cambio de momento angular a lo largo de un eje especificado, es un múltiplo entero de h/2π, donde h es la constante de Planck

${\displaystyle \begin{array}{l}\Delta L_z=n\frac{h}{2\pi }\\ \frac{{\mu }_{0}q{q}_m}{2\pi }=n\frac{h}{2\pi }\\ q_m=\frac{nh}{{\mu }_{0}q}\end{array}}$

Para n=1 e identificando q con la carga del electrón 1.6021·10^-19 C, obtenemos la carga del monopolo

${\displaystyle q_m=\frac{h}{{\mu }_{0}e}=\frac{6.6256·{10}^{-34}}{4\pi {10}^{-7}·1.6021·{10}^{-19}}=\text{ 3}{\text{.2910·10}}^{-9}\text{A·m}}$

Fuerza que ejerce un campo eléctrico sobre un monopolo en movimiento

Una carga eléctrica que se mueve en el seno de un campo magnético experimenta la denominada fuerza de Lorentz, $\overrightarrow{F}=q(\overrightarrow{v}\times \overrightarrow{B})$ . De forma similar, una carga magnética que se mueve en el seno de un campo eléctrico experimenta una fuerza cuya expresión vamos a determinar

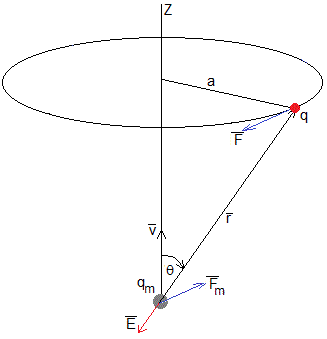
Un monopolo que se mueve con velocidad v produce un campo eléctrico

${\displaystyle \overrightarrow{E_m}=\frac{{\mu }_0{q}_m}{4\pi }\frac{v\times \widehat{r}}{r^2}}$

La carga eléctrica experimenta una fuerza

${\displaystyle \overrightarrow{F}=q\overrightarrow{E_m}=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{v\times \widehat{r}}{r^2}}$

La carga eléctrica q produce en la posición del monopolo un campo eléctrico

${\displaystyle \overrightarrow{E}=-\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}\widehat{r}}$

De acuerdo a la tercera ley de Newton, el monopolo experimenta una fuerza igual y de sentido contrario

${\displaystyle \overrightarrow{F_m}=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{v\times \widehat{r}}{r^2}=-{\mu }_0{\epsilon }_0{q}_m\overrightarrow{v}\times \overrightarrow{E}=-\frac{q_m}{c^2}\overrightarrow{v}\times \overrightarrow{E}}$

Referencias

Magnetic monopole. A problem proposed for the problem competition of WoPhO 2012. 21 June 2012

Carl A. Kocher. Interactions of magnetic monopoles with electric currents. Am. J. Phys. 61 (1993) pp. 875–878