Van de Graaff inventó el generador que lleva su nombre en 1931, con el propósito de producir una diferencia de potencial muy alta (del orden de 20 millones de volts) para acelerar partículas cargadas que se hacían chocar contra blancos fijos. Los resultados de las colisiones nos informan de las características de los núcleos del material que constituye el blanco.

El generador de Van de Graaff es un generador de corriente constante, mientas que la batería es un generador de voltaje constante, lo que cambia es la intensidad dependiendo que los aparatos que se conectan.

El generador de Van de Graaff es muy simple, consta de un motor, dos poleas, una correa o cinta, dos peines o terminales hechos de finos hilos de cobre y una esfera hueca donde se acumula la carga transportada por la cinta.

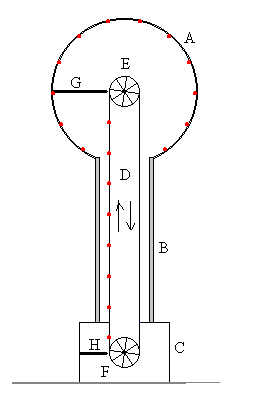
En la figura, se muestra un esquema del generador de Van de Graaff. Un conductor metálico hueco A de forma aproximadamente esférica, está sostenido por soportes aislantes de plástico, atornillados en un pié metálico C conectado a tierra. Una correa o cinta de goma (no conductora) D se mueve entre dos poleas  E y F. La polea F se acciona mediante un motor eléctrico.

Dos peines G y H están hechos de hilos conductores muy finos, están situados a la altura del eje de las poleas. Las puntas de los peines están muy próximas pero no tocan a la cinta.

La rama izquierda de la cinta transportadora se mueve hacia arriba, transporta un flujo continuo de carga positiva hacia el conductor hueco A. Al llegar a G y debido a la propiedad de las puntas se crea un campo lo suficientemente intenso para ionizar el aire situado entre la punta G y la cinta. El aire ionizado proporciona el medio para que la carga pase de la cinta a la punta G y a continuación, al conductor hueco A, debido a la propiedad de las cargas que se introducen en el interior de un conductor hueco (cubeta de Faraday).

Las características del generador de Van de Graaff que disponemos en el laboratorio de Física de la E.U.I.T.I. de Eibar, son los siguientes:

• Diámetro de la esfera conductora 21 cm
• Capacidad 15 pF
• Tensión máxima 150-200 kV
• Máxima corriente 6 μA

Campo producido por un conductor esférico de cargado.

La ley de Gauss afirma que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga en el interior de dicha superficie dividido entre ε₀.

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}}$

Consideremos una esfera hueca de radio R cargada con una carga Q. La aplicación de la ley de Gauss requiere los siguientes pasos:

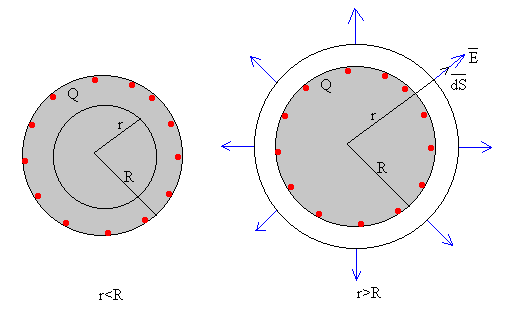
1. A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La distribución de carga tiene simetría esférica luego, la dirección del campo es radial

2. Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, una esfera de radio r.

El campo $\overrightarrow{E}$ es paralelo al vector superficie $\overrightarrow{dS}$ , y el campo es constante en todos los puntos de la superficie esférica por lo que,

${\displaystyle \underset{S}{{\displaystyle \int }}\overrightarrow{E}·\overrightarrow{dS}=\underset{S}{{\displaystyle \int }}E·dS\cos 0º=E\underset{S}{{\displaystyle \int }}dS=E·4\pi r^2}$

El flujo total es  E·4πr²

3. Determinar la carga que hay en el interior de la superficie cerrada

• r<R.  No hay carga en el interior de la esfera de radio r<R, q=0
• r>R. Si estamos calculando el campo en el exterior de la esfera cargada, la carga que hay en el interior de la superficie esférica de radio r es la carga total q=Q.

4. Aplicar la ley de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E=0\text{(}r<R)E=\frac{Q}{4\pi {\epsilon }_0{r}^2}\text{(}r>R)}$

En la figura, se muestra la representación del módulo del campo eléctrico E en función de la distancia radial r.



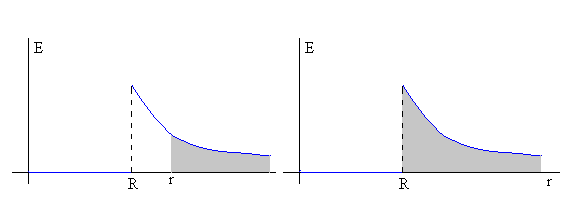
El campo en el exterior de la esfera conductora cargada con carga Q, tiene la misma expresión que el campo producido por una carga puntual Q situada en su centro.

Potencial de la esfera conductora

Se denomina potencial a la diferencia de potencial entre un punto P a una distancia r del centro de la esfera y el infinito.

Como el campo en el interior de le esfera conductora es cero, el potencial es constante en todos sus puntos. El potencial en la superficie de la esfera es el área sombreada (figura de la derecha)

${\displaystyle V={\displaystyle \underset{R}{\overset{\infty }{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}dr=}\frac{Q}{4\pi {\epsilon }_{0}R}}$

Se denomina capacidad de la esfera (más adelante definiremos esta magnitud) al cociente entre la carga y su potencial, C=Q/V=4πε₀R.

Energía de la distribución de cargas

Como la carga Q reside en la superficie esférica y el potencial de dicha carga es V, la energía de la distribución de carga es

${\displaystyle U=\frac{1}{2}QV=\frac{Q^2}{8\pi {\epsilon }_{0}R}}$

Potencia del motor que mueve la correa

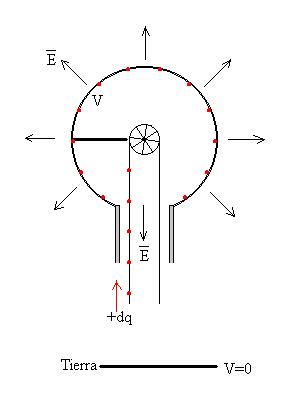
Supóngase que la diferencia de potencial entre el conductor hueco del generador de Van de Graaff y el punto sobre el cual se esparcen las cargas sobre la correa es V. Si la correa proporciona carga positiva a la esfera a razón de i amperes. Determinar la potencia necesaria para mover la polea en contra de las fuerzas eléctrica.

El trabajo que hay que realizar para que una carga dq positiva pase de un lugar en el que el potencial es cero a otro en el que el potencial V es

dW=Vdq

La potencia

${\displaystyle P=\frac{dW}{dt}=V\frac{dq}{dt}=Vi}$

Para el generador de Van de Graaff de nuestro laboratorio que transporta en la correa una carga máxima 6 mC en cada segundo, desde un potencial 0 a un potencial máximo de 200 kV,  la potencia será P=200·10³·6·10^-6=1.2 W

Actividades

Simulamos el generador de Van de Graaff, con la descripción dada en la sección anterior. En el generador real la cinta transporta carga de forma continua. En la simulación, se transporta de forma discreta, sobre la cinta aparecen puntos rojos igualmente espaciados, cada unos de ellos representa una unidad de carga positiva cuyo valor genera el programa interactivo de forma aleatoria.

Al igual que en un generador real, el simulado pone un límite al campo máximo en la superficie de la esfera a partir del cual, el aire se ioniza y el generador no puede incrementar más la carga. Consideramos el conductor hueco como una esfera conductora de radio R. Conociendo la carga acumulada Q se calcula el campo producido por un esfera conductora en su superficie

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{R^2}}$

El generador deja de acumular carga cuando el aire se vuelve conductor. La intensidad del campo eléctrico límite es de aproximadamente 3.0 10⁶ V/m. Para una esfera de radio R calculamos la carga máxima que puede acumular y el máximo potencial que adquiere la esfera cargada.

Se pulsa en el botón titulado Nuevo.

La esfera tiene 50 cm de radio. Comprobamos que

• La carga máxima que puede acumular es Q=83.3 μC hasta que se produce la ruptura dieléctrica (el campo eléctrico límite es de 3.0 10⁶ V/m)
• El máximo potencial V es de 1.5 millones de volts.

Referencias

Francis W. Sears y Mark W. Zemansky. Física, Edt. Aguilar (1970) pág. 565.