Movimiento del c.m. y de las partículas de un sistema

Movimiento del c.m. y de las partículas de un sistema (I)

Esta página y las dos siguientes se estudia un sistema formado por dos partículas unidas por un muelle elástico que tratarán de ayudar a reconocer:

Cuáles son las fuerzas interiores o de interacción entre las partículas del sistema.
Cuáles son las fuerzas exteriores que actúan sobre cada una de las partículas.
Qué fuerzas determinan el movimiento de cada una de las partículas.
Qué fuerzas determinan el movimiento del c.m. del sistema de partículas.

Veremos que el movimiento de cada partícula está determinado por la acción de las fuerzas exteriores al sistema y de las fuerzas de interacción de las otras partículas del sistema sobre la partícula considerada.

Combinaremos las dos ecuaciones del movimiento para obtener:

la ecuación del movimiento del centro de masas del sistema de partículas que se mueve como si fuera una partícula de masa igual a la masa total del sistema bajo la acción de la resultante de las fuerzas exteriores aplicadas al sistema.
el movimiento relativo de las dos partículas depende solamente de las fuerzas interiores o de interacción entre las dos partículas.

Estas dos ecuaciones son fácilmente integrables y nos permiten obtener la posición y velocidad de cada una de las partículas en función del tiempo.

Un segundo ejemplo descrito en esta página, es el sistema formado por dos partículas unidas por un muelle elástico en rotación en el plano horizontal.

Consideremos un sistema simple de partículas consistente en un muelle en posición vertical que tiene una masa M en el extremo superior y una masa m en su extremo inferior. Se supone que la masa del muelle es despreciable. Inicialmente, el muelle de constante k, está en equilibrio sujeto por la masa M tal como se muestra en la figura.

Situación inicial:

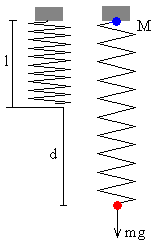
Si l es la longitud del muelle sin deformar, cuando se cuelga de su extremo inferior una masa m, la longitud del muelle se incrementa en d

mg=kd

Para analizar el problema, estableceremos el origen, en la posición inicial de la partícula de masa M, y consideraremos positivas las distancias medidas en sentido descendente.

Ecuación del movimiento de cada una de las partículas:

Cuando se libera la partícula, al cabo de un cierto tiempo t, la posición de la masa inferior m es x y el de la masa superior M es y. Aplicando las leyes de la dinámica a cada una de las partículas vamos a calcular sus posiciones x e y en función del tiempo t.

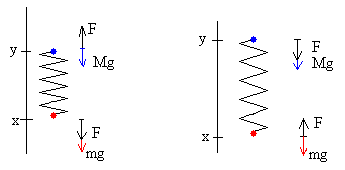
La deformación del muelle en el instante t es l-(x-y) y la fuerza que ejerce el muelle sobre cada una de las partículas es F=k·(l-x+y).

Cuando el muelle está comprimido l>(x-y), la fuerza F=k(l-x+y) es positiva (figura de la izquierda).
Cuando el muelle está estirado l<(x-y), la fuerza F=k(l-x+y) es negativa (figura de la derecha).

Movimiento de la partícula de masa m

$m \frac{d^{2} x}{d t^{2}} = m g + k (l - x + y)$

Condiciones iniciales: para t=0 su velocidad inicial es cero dx/dt=0 y se encuentra en x=l+d

Movimiento de la partícula de masa M

$M \frac{d^{2} y}{d t^{2}} = M g - k (l - x + y)$

Condiciones iniciales: para t=0, su velocidad inicial es cero dy/dt=0 y se encuentra en el origen y=0.

Movimiento del centro de masa del sistema de dos partículas

La posición del centro de masas del sistema de dos partículas es

$z = \frac{m x + M y}{m + M}$

Sumando miembro a miembro las dos ecuaciones diferenciales, llegamos a la ecuación del movimiento del c.m. del sistema

$(m + M) \frac{d^{2} z}{d t^{2}} = m g + M g$

Las condiciones iniciales son: en el instante t=0, la velocidad inicial del c.m. es cero y se encuentra en z₀, cuando el muelle estaba sujeto por la parte superior, x=l+d, y=0.

$z_{0} = \frac{m (l + d)}{m + M} = \frac{m (k l + m g)}{k (m + M)}$

La aceleración del centro de masas es constante e igual a g. La posición del centro de masas en función del tiempo, será.

$z = z_{0} + \frac{1}{2} g t^{2}$

Movimiento relativo de las dos partículas

Multiplicando la primera ecuación del movimiento por M, la segunda por m y restando obtenemos

$\begin{array}{l} M (\frac{d^{2} x}{d t^{2}} - \frac{d^{2} y}{d t^{2}}) = (m + M) k (l - x + y) \\ \frac{m M}{m + M} \frac{d^{2} (x - y)}{d t^{2}} = k (l - (x - y)) \end{array}$

Esta última ecuación nos dice que el movimiento relativo de las dos partículas es equivalente al movimiento de una partícula de masa reducida μ=mM/(m+M) bajo la acción de la fuerza que describe la interacción mutua F=k(l-x+y).

Haciendo el cambio de variable ξ=x-y, tenemos la ecuación diferencial

$μ \frac{d^{2} ξ}{d t^{2}} = k (l - ξ) \frac{d^{2} ξ}{d t^{2}} + \frac{k}{μ} ξ = \frac{k}{μ} l$

La solución de esta ecuación diferencial es

$ξ = l + A \sin (ω t) + B \cos (ω t) ω = \sqrt{\frac{k}{μ}} = \sqrt{\frac{k (m + M)}{m M}}$

Las constantes A y B se determinan a partir de las condiciones iniciales

En el instante t=0, la posición relativa ξ=x-y=l+d, y la velocidad relativa es cero dξ/dt=0. Donde d=mg/k es la deformación inicial del muelle

ξ=l+d·cos(ωt).

Movimiento de cada una de las partículas

Conocida la ecuación del movimiento del centro de masas, y la ecuación del movimiento relativo de las dos partículas, determinamos el movimiento de cada una de las partículas.

$\begin{array}{l} z = \frac{m x + M y}{m + M} = \frac{m (k l + m g)}{k (m + M)} + \frac{1}{2} g t^{2} \\ x - y = l + \frac{m g}{k} \cos (ω t) \end{array}$

Despejamos x e y del sistema de dos ecuaciones,

$\begin{array}{l} x = l + \frac{m^{2} g}{k (m + M)} + \frac{m M g}{k (m + M)} \cos (ω t) + \frac{1}{2} g t^{2} \\ y = \frac{m^{2} g}{k (m + M)} (1 - \cos (ω t)) + \frac{1}{2} g t^{2} \end{array}$

Comprobamos que en el instante t=0, las posiciones iniciales de las partículas son x=l+mg/k, y=0.

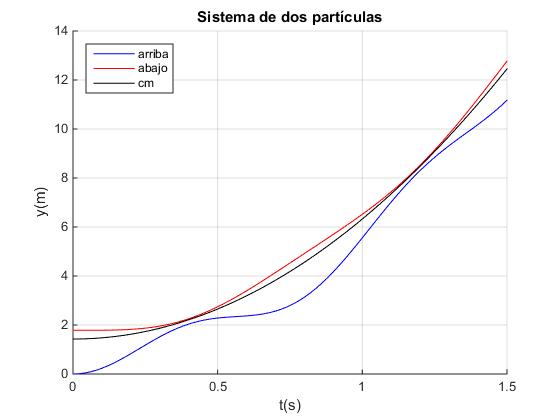
Creamos el siguiente script para representar la posiciones x e y de cada una de las dos partículas y del c.m. z en función del tiempo

M=1.0; %masa arriba
m=4.0;   %masa abajo 
longitud=1.0;  %longitud del muelle sin deformar
k=50;     %constante del muelle
w=sqrt(k*(M+m)/(M*m));

t=0:0.02:1.5;
%posiciones arriba y, abajo x.
y=9.8*t.^2/2+m*m*9.8*(1.0-cos(w*t))/(k*(M+m)); 
x=longitud+m*m*9.8/(k*(M+m))+9.8*t.^2/2+M*m*9.8*cos(w*t)/(k*(M+m));
z=(m*x+M*y)/(m+M);  %centro de masa

hold on
plot(t,y,'blue')
plot(t,x,'red')
plot(t,z,'black')
hold off
legend('arriba','abajo','cm','Location','northwest')

xlabel('t(s)')
ylabel('y(m)')
title('Sistema de dos partículas')
grid on

Las velocidades de las partículas se obtienen derivando x e y respecto del tiempo

$\begin{array}{l} \frac{d x}{d t} = g t - ω \frac{M m g}{k (m + M)} \sin (ω t) \\ \frac{d y}{d t} = g t + ω \frac{m^{2} g}{k (m + M)} \sin (ω t) \end{array}$

En el instante t=0, las partículas están en reposo

Energías

Vamos a comprobar que el trabajo de las fuerzas exteriores (el peso) se invierte en modificar la energía del sistema de partículas, W_ext=U_f-U_i, o bien

W_ext=ΔE_k+ ΔE_p

Variación de energía cinética ΔE_k

Como las partículas están inicialmente en reposo, la variación de energía cinética del sistema formado por las dos partículas es igual a la energía cinética final.

$Δ E_{k} = \frac{1}{2} m {(\frac{d x}{d t})}^{2} + \frac{1}{2} M {(\frac{d y}{d t})}^{2} = \frac{1}{2} (m + M) g^{2} t^{2} + \frac{1}{2} \frac{m^{2} g^{2}}{k} \sin^{2} (ω t)$

Variación de energía potencial ΔE_p

En la situación inicial, el muelle está deformado una longitud d.
En la situación final, la deformación del muelle es l-x+y.

La variación de energía potencial es

$Δ E_{p} = \frac{1}{2} k {(l - x + y)}^{2} - \frac{1}{2} k d^{2} = \frac{1}{2} \frac{m^{2} g^{2}}{k} \cos^{2} (ω t) - \frac{1}{2} \frac{m^{2} g^{2}}{k}$

El trabajo de la fuerza exterior W_ext

El trabajo es el producto de la fuerza (m+M)g por el desplazamiento del c.m. (z-z₀).

$W_{e x t} = (m + M) g (z - z_{0}) = \frac{1}{2} (m + M) g^{2} t^{2}$

Teniendo en cuanta que sin²(ωt)+ cos²(ωt)=1, vemos que se cumple la ecuación que describe el balance energético para el sistema formado por dos partículas unidas por un muelle elástico.

Levitación de la partícula inferior

Observamos que en los primeros instantes del movimiento, la partícula superior (de color azul) y el centro de masa (de color negro) se desplazan, pero la partícula inferior (de color rojo) apenas cambia su posición, parece estar suspendida durante unos instantes en el aire, tal como se puede observar en la figura.

En la ecuación que nos da la posición x de la partícula inferior, supongamos que ωt es pequeño, cos(ωt)≈1

x≈l+mg/k=l+d

La posición de la partícula inferior cambia muy poco en los primeros instantes del movimiento. En la gráfica de la posición x en función del tiempo t, que hemos representado anteriormente utilizando MATLAB, observamos un pequeño segmento horizontal de color rojo.

Actividades

Se introduce:

La masa M de la partícula, en el control titulado Masa arriba.
La masa m de la otra partícula, en el control titulado Masa abajo.
La constante k del muelle elástico, en el control titulado Cte. muelle.
La longitud del muelle sin deformar se ha fijado en el programa en l=1 m.

Se pulsa el botón titulado Nuevo.

Observamos el movimiento de cada una de las dos partículas (señalados por círculos de color azul y rojo) y la del centro de masa del sistema (en color negro).

El programa verifica los datos que introduce el usuario de modo que la deformación máxima del muelle no pueda ser mayor que su longitud inicial l.

Se muestra también como se distribuye la energía total del sistema aislado entre:

Energía cinética y potencial de la partícula de arriba (azul), A
Energía cinética y potencial de la partícula de abajo (roja), B
Energía almacenada en el muelle elástico deformado (gris)

Ejemplo:

Se introduce

m=4 kg
M=1 kg
k=50 N/m
La longitud inicial del muelle sin deformar es l=1.0 m

Calcular las posiciones de las partículas y la del centro de masa en el instante t=1 s.

$ω = \sqrt{\frac{50 (1 + 4)}{1 \cdot 4}} = 7.9 rad/s$

Las posiciones de las partículas son

$\begin{array}{l} x = 1.0 + \frac{1}{2} 9.8 \cdot 1^{2} + 4 \cdot 9.8 \frac{4 + 1 \cdot \cos (7.9 \cdot 1)}{50 (4 + 1)} = 6.52 m \\ y = \frac{1}{2} 9.8 \cdot 1^{2} + \frac{4^{2} \cdot 9.8}{50 (4 + 1)} (1 - \cos (7.9 \cdot 1)) = 5.56 m \end{array}$

Conocida la posición de las partículas de masas m=4 y M=1 kg calculamos la posición del c.m.

$z = \frac{4 \cdot 6.52 + 1 \cdot 5.56}{4 + 1} = 6.33 m$

La posición inicial del centro de masa es

$z_{0} = \frac{4 (50 \cdot 1 + 4 \cdot 9.8)}{50 (4 + 1)} = 1.43 m$

La posición del c.m. en el instante t=1 es

$z = 1.43 + \frac{1}{2} 9.8 \cdot 1^{2} = 6.33 m$

Masa arriba (kg): Masa abajo (kg)
Cte. muelle

Dos partículas unidas por un muelle elástico en movimiento de rotación

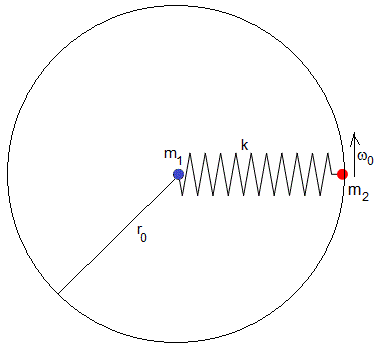
Sean dos partículas de masas m₁ y m₂ unidas por un muelle elástico de constante k y de longitud l₀ sin deformar, la primera está en el origen y la segunda describe una circunferencia de radio r₀ en el plano horizontal. Aplicando la dinámica del movimiento circular uniforme

$\begin{array}{l} m_{2} ω_{0}^{2} r_{0} = k (r_{0} - l_{0}) \\ r_{0} = \frac{l_{0}}{1 - \frac{m_{2} ω_{0}^{2}}{k}} \end{array}$

Como r₀ es positivo, la fracción en el denominador tiene que ser menor que la unidad

En el instante t=0, soltamos la partícula que está en el origen. Vamos a analizar el movimiento de dos partículas bajo la fuerza de interacción F.

$F = k (r - l_{0})$

Donde r es la longitud del muelle

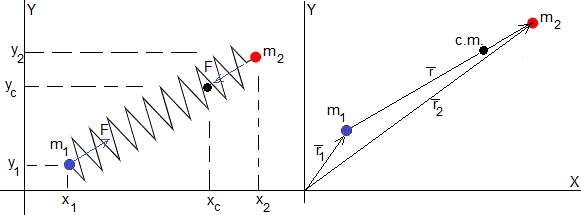
Consideremos ahora un sistema aislado formado por dos cuerpos: un cuerpo de masa m₁ y otro cuerpo de masa m₂ bajo la acción de la fuerza de atracción mutua F.

Cada cuerpo se mueve bajo la acción de dicha fuerza

$m_{1} \frac{d^{2} \vec{r_{1}}}{d t^{2}} = \vec{F,} m_{2} \frac{d^{2} \vec{r_{2}}}{d t^{2}} = \vec{- F}$

Restamos la segunda ecuación de la primera

$\begin{array}{l} \frac{d^{2} (\vec{r_{2}} - \vec{r_{1}})}{d t^{2}} = - \frac{\vec{F}}{m_{2}} - \frac{\vec{F}}{m_{1}} \\ \frac{d^{2} \vec{r}}{d t^{2}} = - \vec{F} (\frac{m_{1} + m_{2}}{m_{1} m_{2}}) \\ μ \frac{d^{2} \vec{r}}{d t^{2}} = - F \hat{r} \end{array}$

Donde μ se denomina masa reducida, y $\vec{r}$ es el vector posición de la segunda partícula respecto de la primera,

En coordenadas polares la aceleración se escribe

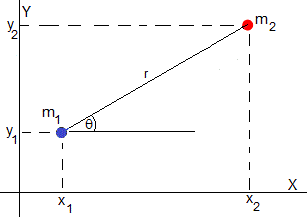
$\frac{d^{2} \vec{r}}{d t^{2}} = \frac{d \vec{v}}{d t} = (\frac{d^{2} r}{d t^{2}} - r {(\frac{d θ}{d t})}^{2}) \hat{r} + (r \frac{d^{2} θ}{d t^{2}} + 2 \frac{d r}{d t} \frac{d θ}{d t}) \hat{θ}$

Las ecuaciones diferenciales del movimiento relativo son

${\begin{cases} \frac{d^{2} r}{d t^{2}} - r {(\frac{d θ}{d t})}^{2} = - \frac{k}{μ} (r - l_{0}) \\ r \frac{d^{2} θ}{d t^{2}} + 2 \frac{d r}{d t} \frac{d θ}{d t} = 0 \end{cases}$

Se resuelven mediante procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, r=r₀, dr/dt=0; θ=0, dθ/dt=ω₀

Las posiciones del centro de masas (c.m.) y de cada una de las partículas vienen dadas por las siguientes expresiones

$\begin{array}{l} \vec{R} = \frac{m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}}}{m_{1} + m_{2}}, \vec{r} = \vec{r_{2}} - \vec{r_{1}} \\ \vec{r_{1}} = \vec{R} - \frac{m_{2}}{m_{1} + m_{2}} \vec{r}, \vec{r_{2}} = \vec{R} + \frac{m_{1}}{m_{1} + m_{2}} \vec{r} \end{array}$

De modo similar, obtenemos la velocidad del c.m. y de cada una de las partículas

$\begin{array}{l} \vec{V_{c m}} = \frac{m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}}{m_{1} + m_{2}}, \vec{v} = \vec{v_{2}} - \vec{v_{1}} \\ \vec{v_{1}} = \vec{V_{c m}} - \frac{m_{2}}{m_{1} + m_{2}} \vec{v}, \vec{v_{2}} = \vec{V_{c m}} + \frac{m_{1}}{m_{1} + m_{2}} \vec{v} \end{array}$

En el instante t=0, la primera partícula se encuentra en el origen (0,0) y la segunda en la posición (r₀, 0). La posición inicial del centro de masas es

$\vec{R} = \frac{m_{2}}{m_{1} + m_{2}} r_{0} \hat{i}$

En el instante t=0, la primera partícula se encuentra en reposo y la segunda se mueve con velocidad ω₀r₀ en la dirección del eje Y. La velocidad constante del centro de masas es

$\vec{V_{c m}} = \frac{m_{2}}{m_{1} + m_{2}} ω_{0} r_{0} \hat{j}$

El movimiento del centro de masas es rectilíneo y uniforme

$\vec{R} = \frac{m_{2}}{m_{1} + m_{2}} r_{0} \hat{i} + \frac{m_{2}}{m_{1} + m_{2}} ω_{0} r_{0} t \hat{j}$

La posición de la primera partícula es

$\begin{array}{l} \vec{r_{1}} = \vec{R} - \frac{m_{2}}{m_{1} + m_{2}} \vec{r} = \frac{m_{2}}{m_{1} + m_{2}} r_{0} \hat{i} + \frac{m_{2}}{m_{1} + m_{2}} ω_{0} r_{0} t \hat{j} - \frac{m_{2}}{m_{1} + m_{2}} (r \cos θ \hat{i} + r \sin θ \hat{j}) \\ {\begin{cases} x_{1} = \frac{m_{2}}{m_{1} + m_{2}} (r_{0} - r \cos θ) \\ y_{1} = \frac{m_{2}}{m_{1} + m_{2}} (ω_{0} r_{0} t - r \sin θ) \end{cases} \end{array}$

La posición de la segunda partícula es

$\begin{array}{l} \vec{r_{2}} = \vec{R} + \frac{m_{1}}{m_{1} + m_{2}} \vec{r} = \frac{m_{2}}{m_{1} + m_{2}} r_{0} \hat{i} + \frac{m_{2}}{m_{1} + m_{2}} ω_{0} r_{0} t \hat{j} + \frac{m_{1}}{m_{1} + m_{2}} (r \cos θ \hat{i} + r \sin θ \hat{j}) \\ {\begin{cases} x_{2} = \frac{m_{2} r_{0} + m_{1} r \cos θ}{m_{1} + m_{2}} \\ y_{2} = \frac{m_{2} ω_{0} r_{0} t + m_{1} r \sin θ}{m_{1} + m_{2}} \end{cases} \end{array}$

Resultados

Los datos son

Masa de la primera partícula, m₁= 5 g
Masa de la segunda partícula, m₂= 25 g
Constante del muelle, k=0.3 N/m
Longitud del muelle sin deformar, l₀=0.5 m
Velocidad angular de rotación, ω₀=1.6755 rad/s

Calculamos la longitud inicial del muelle r₀

Resolvemos el sistema de ecuaciones diferenciales por el procedimiento ode45 de MATLAB, con las condiciones iniciales: r=r₀, dr/dt=0, θ=0, dθ/dt=ω₀

Representamos

En color azul, la trayectoria de la primera partícula, que parte del origen
En color rojo, la trayectoria de la segunda partícula que parte de la posición (r₀, 0)
En color verde, la trayectoria rectilínea del centro de masas
En color negro a trazos, el arco de circunferencia de radio r₀

m1=5/1000; %masas
m2=25/1000;
mu=m1*m2/(m1+m2); %masa reducida
l0=0.5; %longitud sin deformar
k=0.3; %constante del muelle
wn=sqrt(k/mu);%frecuencia propia
w0=1.6755; %velocidad angular de rotación
r0=l0/(1-m2*w0^2/k); %longitud inicial del muelle
fg=@(t,x)[x(2);x(1)*x(4)^2-k*(x(1)-l0)/mu; x(4);-2*x(2)*x(4)/x(1)];
[t,x]=ode45(fg,[0,0.3],[r0, 0, 0,w0]);
xC=m2*r0/(m1+m2);
yC=m2*w0*r0*t/(m1+m2);
x1=xC-m2*x(:,1).*cos(x(:,3))/(m1+m2);
y1=yC-m2*x(:,1).*sin(x(:,3))/(m1+m2);
x2=xC+m1*x(:,1).*cos(x(:,3))/(m1+m2);
y2=yC+m1*x(:,1).*sin(x(:,3))/(m1+m2);
hold on
fplot(@(t) r0*cos(t), @(t) r0*sin(t),[0,pi/6], 'color','k','lineStyle','--')
plot(x1,y1,'b') %partícula m1
plot(x2,y2,'r') %partícula m2
plot(ones(1,length(yC))*xC,yC,'g') %centro de masas
hold off
grid on
axis equal
xlabel('x')
ylabel('y');
title('Sistema de dos partículas')

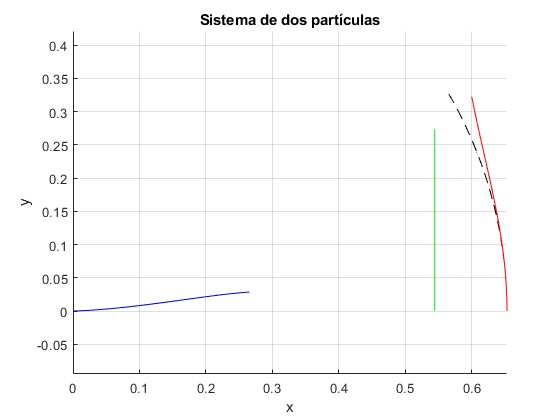
Cuando se libera la primera partícula, la segunda sigue, durante un pequeño intervalo de tiempo, describiendo aproximadamente su trayectoria inicial, un arco de circunferencia de radio r₀

Reproducimos la figura 2 del artículo de Batista, representando, la distancia r entre las dos partículas (longitud del muelle) y la distancia de la segunda partícula al origen en función del tiempo t. La línea recta a trazos es el radio r₀, longitud inicial del muelle

Añadimos al código anterior

...
figure
hold on
plot(t,x(:,1))
line([0,t(end)],[r0,r0],'lineStyle','--')
d=sqrt(x2.^2+y2.^2);
plot(t,d)
hold off
grid on
xlabel('t')
ylabel('r');
title('Longitud del muelle')

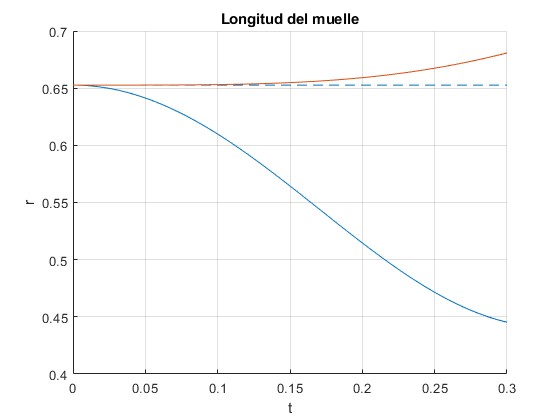
La distancia entre el origen y la segunda partícula casi no cambia, es próxima a r₀ durante un intervalo de tiempo

Referencias

Glaister. Oscillations of a falling spring. Phys. Educ. V-28 (5) 1993, pp. 329-33

Milan Batista. The initial trajectory of a ball released from uniform circular motion. Eur. J. Phys. 45 (2024) 035001