Movimiento de rodar sin deslizar

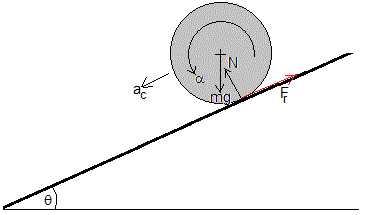
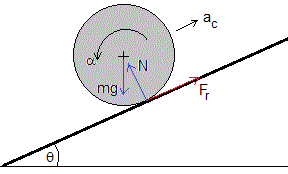
Examinaremos el movimiento de un cuerpo (un aro, un cilindro o una esfera) que rueda a lo largo de un plano inclinado.

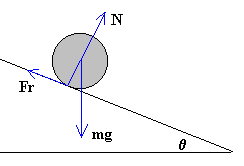
Las fuerzas que actúan sobre el cuerpo son:

• el peso
• la reacción del plano inclinado
• la fuerza de rozamiento en el punto de contacto entre la rueda y el plano.

Descomponemos el peso en una fuerza a lo largo del plano y otra perpendicular al plano inclinado. Las ecuaciones del movimiento son la siguientes:

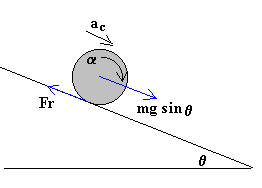
• Movimiento de traslación del c.m.

mg·sinθ -F_r=ma_c

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

F_rR=I_cα

• Relación entre el movimiento de traslación y rotación (rueda sin deslizar)

a_c=α·R

Si conocemos el ángulo de inclinación θ  y el momento de inercia I_c del cuerpo que rueda, calculamos a_c y el valor de la fuerza de rozamiento F_r.

Expresamos el momento de inercia I_c=k·mR² donde k es un factor geométrico 2/5 para la esfera, 1/2 para el cilindro y 1 para el aro.

${\displaystyle a_c=\frac{g·\text{sin}\theta }{1+k}{F}_r=k\frac{mg·\text{sin}\theta }{\text{1}+k}}$

Si deseamos calcular la velocidad del cuerpo después de haber recorrido una longitud x a lo largo del plano inclinado, partiendo del reposo, empleamos las ecuaciones de la del movimiento rectilíneo uniformemente acelerado

${\displaystyle x=\frac{1}{2}{a}_c{t}^2{v}_c=a_{c}t}$

La velocidad final v_c del c. m. del cuerpo al llegar al final del plano inclinado es

${\displaystyle v_c^2=2a_{c}x=\frac{2g\text{sin}\theta }{1+k}x=\frac{2gh}{1+k}}$

Siendo h la altura de partida del cuerpo referida a la posición final, h=x·senθ

Balance de energía

• Energía cinética en el movimiento de rodar

La energía cinética de un cuerpo que rueda es la suma de la energía cinética de traslación del c.m. y la energía cinética de rotación alrededor del c.m.

${\displaystyle E_k=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\omega }^2}$

• Trabajo de las fuerzas que actúan sobre el cuerpo

El trabajo total de las fuerzas que actúan sobre el cuerpo que rueda es la suma del trabajo en el movimiento de traslación más el trabajo en el movimiento de rotación

W=W_t+W_r

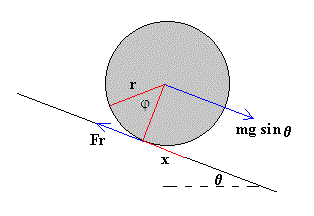
El trabajo en el movimiento de traslación es

W_t=(mgsinθ -F_r)x=mgh-F_rx

El trabajo en el movimiento de rotación es

W_r=Mφ =F_rRφ =F_rx

El trabajo total es

W=mgh

Como vemos la fuerza de rozamiento en el movimiento de rodar produce dos trabajos de la misma magnitud pero de signos opuestos. Esta es la razón por la que no tenemos que incluir el trabajo de la fuerza de rozamiento en el balance de energía.

El trabajo de la resultante de las fuerzas que actúan sobre un cuerpo modifica su energía cinética (de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m.)

${\displaystyle mgh=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\omega }^2}$

La velocidad final v_c del c. m. del cuerpo al llegar al final del plano inclinado es la misma que hemos calculado a partir de la dinámica.

${\displaystyle mgh=\frac{1}{2}m{v}_c^2+\frac{1}{2}km{R}^2\frac{v_c^2}{R^2}{v}_c^2=\frac{2gh}{1+k}}$

El cuadrado de la velocidad del c.m. v_c es proporcional a la altura inicial h. Comprobaremos esta relación en el programa interactivo al final de esta página.

Movimiento de rodar con deslizamiento

Cuando un cuerpo rueda sin deslizar, la fuerza de rozamiento F_r es desconocida y se calcula resolviendo las ecuaciones del movimiento, tal como hemos visto en el apartado movimiento de rodar sin deslizar

${\displaystyle F_r=k\frac{mg\sin \theta }{1+k}}$

Para que haya movimiento de rodar sin deslizar se tiene que cumplir que F_r≤ µ_s·N

Donde µ_s es el coeficientede rozamiento estático que depende de la naturaleza de los cuerpos en contacto, la rueda y el carril, y N la reacción del plano inclinado N=mg·cosθ .

El cuerpo rueda sin deslizar por el plano inclinado θ si se cumple que

${\displaystyle {\mu }_s\ge \frac{k\tan \theta }{1+k}}$

El ángulo crítico se calcula mediante la fórmula

${\displaystyle \tan {\theta }_c=\frac{{\mu }_s(1+k)}{k}}$

Ejemplo:

• El cuerpo es un cilindro, k=0.5
• El coeficiente de rozamiento μ= μ_s= μ_k=0.15
• Distancia que recorre el cuerpo a lo largo del plano inclinado x=1 m

El ángulo crítico θ_c =24.2º

Ecuaciones de la dinámica

Si el ángulo del plano inclinado θ>θ_c, el cuerpo rueda y desliza, la fuerza de rozamiento toma el valor F_r=µ_k·N. Donde µ_k es el coeficiente cinético.

Las ecuaciones del movimiento del centro de masa del cuerpo son ahora:

• Movimiento de traslación del c.m.

mg·sinθ -µ_k·mg·cosθ =ma_c.

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

µ_k·mg·cosθ·R=I_c·α

Despejamos a_c y α

${\displaystyle a_c=g(\sin \theta -{\mu }_k\cos \theta )\alpha =\frac{g{\mu }_k\cos \theta }{k·R}}$

Se deja de cumplir la condición de rodar sin deslizar a_c=α·R.

La velocidad final v_c del c. m. del cuerpo al llegar al final del plano inclinado después de haber recorrido una distancia x, o haber descendido una altura h.

${\displaystyle v_c^2=2a_{c}x=2gh(1-{\mu }_k\cot \theta )}$

La velocidad angular ω del cuerpo después de haber girado un ángulo φ es

${\displaystyle {\omega }^2=2\alpha \phi =\frac{2g{\mu }_k\cos \theta }{k·R}\phi }$

Balance energético

La energía inicial del cuerpo es la energía potencial mgh

La energía final del cuerpo es la suma de la energía cinética de traslación del c.m., más la energía cinética de rotación alrededor del c.m.

${\displaystyle \frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\omega }^2=\frac{1}{2}m\left(v_c^2+k{R}^2{\omega }^2\right)}$

Trabajo W_r de la fuerza de rozamiento F_r=µ_k·mg·cosθ

• En el movimiento de traslación

-F_r·x

• En el movimiento de rotación

F_r·R·φ

El trabajo total es

${\displaystyle \begin{array}{l}{W}_r=-{\mu }_k·mg\cos \theta (x-R\phi )=-{\mu }_k·mg\cos \theta (x-R\frac{{\omega }^2}{2\alpha })=\\ -{\mu }_k·mg\cos \theta \frac{h}{\sin \theta }+\frac{1}{2}mk{R}^2{\omega }^2\end{array}}$

El trabajo de la fuerza de rozamiento modifica la energía del cuerpo y es igual a la diferencia entre la energía final e inicial del cuerpo, W_r=E_f-E_i

${\displaystyle \begin{array}{l}-{\mu }_k·mg\cos \theta \frac{h}{\sin \theta }+\frac{1}{2}mk{R}^2{\omega }^2=\frac{1}{2}m\left(v_c^2+k{R}^2{\omega }^2\right)-mgh\\ v_c^2=2gh(1-{\mu }_k\cot \theta )\end{array}}$

Se anula el trabajo de la fuerza de rozamiento correspondiente al movimiento de rotación F_r·R·φ con la energía cinética de rotación. Obtenemos la misma expresión para la velocidad del c.m. v_c que la deducida a partir de las ecuaciones de la dinámica.

Velocidad final del c.m. en función de la altura h

• Si el ángulo del plano inclinado θ≤θ_c el cuerpo rueda sin deslizar

La velocidad final v_c que alcanza el cuerpo en función de su altura inicial h es

${\displaystyle v_c^2=\frac{2g}{1+k}h}$

El cuadrado de la velocidad del c.m. es proporcional a la altura h

• Si el ángulo del plano inclinado θ>θ_c el cuerpo rueda y desliza

${\displaystyle v_c^2=2gh(1-{\mu }_k\cot \theta )}$

siendo x la distancia fija que recorre el cuerpo a lo largo del plano inclinado

Actividades

Se introduce

• El cuerpo que va a moverse sobre el plano inclinado, un aro, un cilindro o una esfera de la misma masa y radio, en el control titulado Cuerpo
• El valor del coeficiente de rozamiento, en el control Coef. rozamiento.
• El ángulo de inclinación, en el control Ángulo.

• La distancia que recorre el cuerpo a lo largo del plano inclinado se mantiene fija x=1 m

Se pulsa el botón titulado Nuevo.

En la parte derecha, se representa en un diagrama en forma de tarta la energía potencial, la energía cinética de rotación y la energía cinética de traslación del c.m.

• Cuando el cuerpo baja rodando sin deslizar la energía potencial va disminuyendo y se va incrementando la energía cinética (de rotación y traslación en distintas proporciones dependiendo del momento de inercia del cuerpo).

• Cuando el cuerpo baja rodando a la vez que desliza, una parte de la energía potencial se transforma en trabajo de la fuerza de rozamiento.

Ejemplo 1

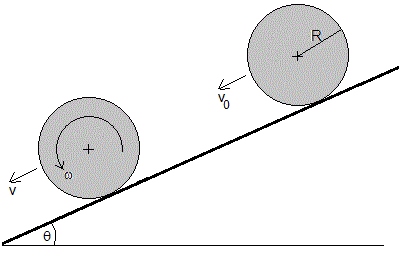
Sea un cilindro (I_c=mR²/2) de masa m y radio R. Se pone en contacto con un plano inclinado θ con la horizontal. El coeficiente de rozamiento entre el cilindro y el plano es μ_k.

Se le proporciona una velocidad v₀. Vamos a determinar el instante t₁ en el que el cilindro empieza a rodar sin deslizar, su posición x₁ y velocidad v₁en dicho instante

A partir de dicho instante t>t₁ el cilindro rueda sin deslizar

Movimiento de rodar deslizando

Cuando se pone en contacto el cilindro con el plano inclinado, no se cumple la condición de rodar sin deslizar. Aparece una fuerza de rozamiento F_r=μ_kN=μ_kmgcosθ que va a restablecer dicha condición. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\begin{array}{l}\{\begin{array}{l}mg\sin \theta -F_r=m{a}_c\\ F_r·r=\frac{1}{2}m{R}^2·\alpha \end{array}\\ a_c=g(\sin \theta -{\mu }_k\cos \theta )\end{array}\hfill \\ \alpha =\frac{2{\mu }_{k}g\cos \theta }{R}\hfill \end{array}}$

La velocidad v del centro de masa y la velocidad angular de rotación ω en el instante t son

${\displaystyle \begin{array}{l}v=v_0+g(\sin \theta -{\mu }_k\cos \theta )t\hfill \\ \omega =\frac{2{\mu }_{k}g\cos \theta }{R}t\hfill \end{array}}$

La condición de rodar sin deslizar v=ωR, se establece en el instante t₁

${\displaystyle \begin{array}{l}{v}_0+g(\sin \theta -{\mu }_k\cos \theta )t_1=R\frac{2{\mu }_{k}g\cos \theta }{R}{t}_1\hfill \\ t_1=\frac{v_0}{g(3{\mu }_k\cos \theta -\sin \theta )}\hfill \end{array}}$

Para que se establezca esta condición, se tiene que cumplir que 3μ_kcosθ>sinθ, tanθ<3μ_k

La velocidad v₁ del c.m. y la angular del cilindro en este instante t₁ son

${\displaystyle \begin{array}{l}{v}_1=v_0\frac{2{\mu }_k\cos \theta }{3{\mu }_k\cos \theta -\sin \theta }\\ {\omega }_1=\frac{v_1}{R}\end{array}}$

El cilindro se habrá desplazado en este tiempo t₁

${\displaystyle x_1=v_0{t}_1+\frac{1}{2}{a}_c{t}_1^2=\frac{v_0^2}{2g}\frac{5{\mu }_k\cos \theta -\sin \theta }{{\left(3{\mu }_k\cos \theta -\sin \theta \right)}^2}}$

Movimiento de rodar sin deslizar

Las ecuaciones del movimiento son

${\displaystyle \{\begin{array}{l}mg\sin \theta -F_r=m{a}_c\\ F_r·r=\frac{1}{2}m{r}^2·\alpha \\ a_c=\alpha r\end{array}}$

Eliminamos la fuerza de rozamiento F_r del sistema de ecuaciones que ahora es una magnitud desconocida

${\displaystyle \begin{array}{l}{a}_c=\frac{2}{3}g\sin \theta \\ \alpha =\frac{2}{3}\frac{g\sin \theta }{R}\end{array}}$

La velocidad del c.m. del cilindro en función del tiempo, para t>t₁

${\displaystyle \begin{array}{l}v=v_1+\frac{2}{3}g\sin \theta \left(t-t_1\right)=v_0\frac{2{\mu }_k\cos \theta }{3{\mu }_k\cos \theta -\sin \theta }+\frac{2}{3}g\sin \theta \left(t-\frac{v_0}{g(3{\mu }_k\cos \theta -\sin \theta )}\right)=\\ v=v_0\frac{6{\mu }_k\cos \theta -2\sin \theta }{3\left(3{\mu }_k\cos \theta -\sin \theta \right)}+\frac{2}{3}g\sin \theta ·t\\ \omega =\frac{v}{R}\end{array}}$

Energías

La energía inicial en el instante t=0

${\displaystyle E_0=\frac{1}{2}m{v}_0^2}$

La energía en el instante t

${\displaystyle E=\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{1}{2}m{R}^2\right){\omega }^2-mgx\sin \theta }$

Hemos establecido el nivel cero de energía potencial en la posición inicial

La energía en el instante t≤t₁ es igual a la energía inicial E₀ menos la energía perdida a causa del rozamiento

${\displaystyle E=E_0-{\mu }_k·mg\cos \theta (x-R\phi )}$

En el instante t₁ la energía del cilindro vale

${\displaystyle \begin{array}{l}{E}_1=\frac{1}{2}m{v}_1^2+\frac{1}{2}\left(\frac{1}{2}m{R}^2\right){\omega }_1^2-mg{x}_1\sin \theta =\frac{1}{2}m{v}_1^2+\frac{1}{2}\left(\frac{1}{2}m{R}^2\right)\frac{v_1^2}{R^2}-mg{x}_1\sin \theta \\ E_1=\frac{3}{4}m{v}_1^2-mg{x}_1\sin \theta \\ E_1=\frac{1}{2}m{v}_0^2-{\mu }_k·mg\cos \theta (x_1-R{\phi }_1)\end{array}}$

Introduciendo x₁, v₁ y φ₁, comprobamos que se obtiene el mismo resultado

${\displaystyle \begin{array}{l}{E}_1=\frac{3}{4}m{v}_1^2-mg{x}_1\sin \theta =\frac{1}{2}m{v}_0^2\frac{6{\mu }_k^2{\cos }^2\theta +{\sin }^2\theta -5{\mu }_k\sin \theta \cos \theta }{{\left(3{\mu }_k\cos \theta -\sin \theta \right)}^2}\\ E_1=\frac{1}{2}m{v}_0^2-{\mu }_k·mg\cos \theta (x_1-r{\phi }_1)=\frac{1}{2}m{v}_0^2\frac{6{\mu }_k^2{\cos }^2\theta +{\sin }^2\theta -5{\mu }_k\sin \theta \cos \theta }{{\left(3{\mu }_k\cos \theta -\sin \theta \right)}^2}\end{array}}$

La energía en el instante t>t₁ se mantiene constante e igual a E₁

${\displaystyle E_1=\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{1}{2}m{R}^2\right){\omega }^2-mgx\sin \theta ,t\ge t_1}$

Ejemplo

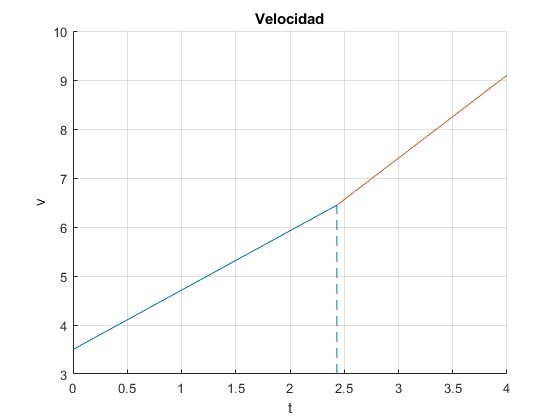
Sea un cilindro de masa m=0.1 kg, y radio R=0.3 m se coloca sobre un plano inclinado de θ=15°. El coeficiente de rozamiento es μ_k=0.14, que cumple la condición, tanθ<3μ_k

En el instante t=0, se le proporciona una velocidad inicial v₀=3.5 m/s sobre una plano

En el instante t₁= 2.4317 s el cilindro empieza a rodar sin deslizar. Representamos la velocidad del cilindro en función del tiempo hasta el instante t=4 s

th=pi/12; %ángulo del plano inclinado
m=0.1; %masa
R=0.3; %radio
v0=3.5; %velocidad inicial
mu_k=0.14; %coeficiente rozamiento
%para t<t1
t1=v0/(9.8*(3*mu_k*cos(th)-sin(th)));
hold on
v=@(t) v0+9.8*(sin(th)-mu_k*cos(th))*t;
fplot(v,[0,t1])
%para t>t1
v=@(t) v0*(6*mu_k*cos(th)-2*sin(th))/(3*(3*mu_k*cos(th)-sin(th)))+
2*9.8*sin(th)*t/3;
line([t1,t1],[3, v(t1)],'lineStyle','--')
fplot(v,[t1,4])
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

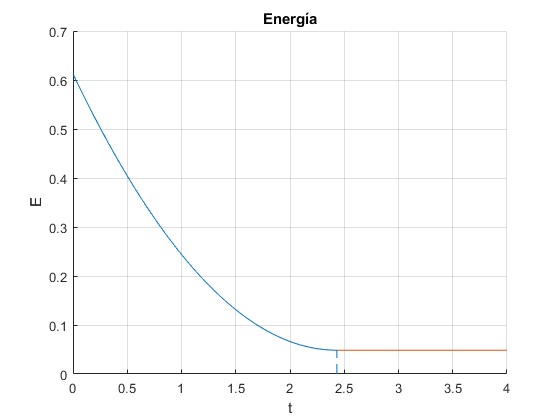
Representamos la energía del cilindro en función del tiempo hasta el instante t=4 s

th=pi/12; %ángulo del plano inclinado
m=0.1; %masa
R=0.3; %radio
v0=3.5; %velocidad inicial
mu_k=0.14; %coeficiente rozamiento
%para t<t1
ac=9.8*(sin(th)-mu_k*cos(th));
alfa=2*mu_k*9.8*cos(th)/R;
v=@(t) v0+ac*t;
w=@(t) alfa*t;
x=@(t) v0*t+ac*t.^2/2;
phi=@(t) alfa*t.^2/2;
E=@(t) m*v(t).^2/2+m*R^2*w(t).^2/4-m*9.8*x(t)*sin(th);
t1=v0/(9.8*(3*mu_k*cos(th)-sin(th)));
hold on
fplot(E,[0,t1])
%para t>t1
ac=2*9.8*sin(th)/3;
v=@(t) v(t1)+ac*(t-t1);
x=@(t) x(t1)+v1*(t-t1)+ac*(t-t1).^2/2;
E=@(t) 3*m*v(t).^2/4-m*9.8*x(t)*sin(th);
fplot(E,[t1,4])
line([t1,t1],[0, E(t1)],'lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('E')
title('Energía')

Ejemplo 2

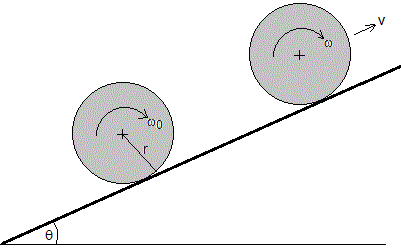
Se proporciona a un cilindro (I_c=mR²/2) de masa m y radio R una velocidad angular de rotación, ω₀.

A continuación, se pone en contacto con un plano inclinado θ con la horizontal. El coeficiente de rozamiento entre el cilindro y el plano es μ_k.

Supondremos que μ_k=μ_s>tanθ.

Determinaremos

• La distancia que recorrerá el cilindro a lo largo del plano hasta que se establezca la condición de rodar sin deslizar
• La máxima distancia que recorre a lo largo del plano hasta que se detiene.

Movimiento de rodar deslizando

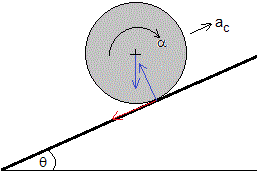
Cuando se pone en contacto el cilindro con el plano inclinado, no se cumple la condición de rodar sin deslizar. Aparece una fuerza de rozamiento F_r=μ_kN=μ_kmgcosθ que va a restablecer dicha condición. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{F}_r-mg\sin \theta =m{a}_c\\ -F_r·R=\left(\frac{1}{2}m{R}^2\right)\alpha \end{array}\\ \{\begin{array}{l}{a}_c=g\left({\mu }_k\cos \theta -\sin \theta \right)\\ \alpha =-\frac{2{\mu }_{k}g\cos \theta }{R}\end{array}\end{array}}$

Dado que μ_k>tanθ, entonces, μ_kmgcosθ>mgsinθ

La velocidad v del centro de masa y la velocidad angular de rotación ω en el instante t son

${\displaystyle \begin{array}{l}v=g\left({\mu }_k\cos \theta -\sin \theta \right)t\\ \omega ={\omega }_0-\frac{2{\mu }_{k}g\cos \theta }{R}t\end{array}}$

La condición de rodar sin deslizar v=ωR, se establece en el instante t₁

${\displaystyle \begin{array}{l}g\left({\mu }_k\cos \theta -\sin \theta \right)t_1=\left({\omega }_0-\frac{2{\mu }_{k}g\cos \theta }{r}{t}_1\right)R\\ t_1=\frac{{\omega }_{0}R}{g\left(3{\mu }_k\cos \theta -\sin \theta \right)}\end{array}}$

La velocidad v₁ del c.m. y la angular del cilindro en este instante t₁ son

${\displaystyle \begin{array}{l}{v}_1=\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R\\ {\omega }_1=\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_0\end{array}}$

El cilindro se habrá desplazado en este tiempo

${\displaystyle x_1=\frac{1}{2}{a}_c{t}_1^2=\frac{{\mu }_k\cos \theta -\sin \theta }{2g{\left(3{\mu }_k\cos \theta -\sin \theta \right)}^2}{\omega }_0^2{R}^2}$

Movimiento de rodar sin deslizar

El cuerpo rueda sin deslizar por el plano inclinado θ si se cumple que

${\displaystyle {\mu }_s\ge \frac{k\tan \theta }{1+k}}$

con k=1/2 para un cilindro macizo

${\displaystyle {\mu }_s\ge \frac{\tan \theta }{3}}$

Hemos supuesto que μ_s>tanθ, luego el cilindro se mueve rodando sin deslizar una vez que se ha establecido esta condición en el instante t₁

Las ecuaciones del movimiento son

${\displaystyle \{\begin{array}{l}-F_r-mg\sin \theta =m{a}_c\\ F_r·R=\left(\frac{1}{2}m{R}^2\right)\alpha \\ a_c=\alpha R\end{array}}$

Eliminamos la fuerza de rozamiento F_r del sistema de ecuaciones que ahora es una magnitud desconocida

${\displaystyle \{\begin{array}{l}{a}_c=-\frac{2}{3}g\sin \theta \\ \alpha =-\frac{2}{3}\frac{g\sin \theta }{R}\end{array}}$

La posición y velocidad del c.m. del cilindro en función del tiempo para t>t₁

${\displaystyle \begin{array}{l}v=v_1-\frac{2}{3}g\sin \theta ·t\\ x=x_1+v_{1}t-\frac{1}{3}g\sin \theta t^2\end{array}}$

El cilindro se detiene en el instante t₂ cuando v=0

${\displaystyle t_2=t_1+\frac{3}{2g\sin \theta }\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R=\frac{{\omega }_{0}R}{2g\sin \theta }}$

La posición final x₂ en dicho instante es

${\displaystyle \begin{array}{l}{x}_2=x_1+\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R\frac{3}{2g\sin \theta }\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R-\frac{1}{3}g\sin \theta {\left(\frac{3}{2g\sin \theta }\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R\right)}^2\\ x_2=\frac{{\mu }_k\cos \theta -\sin \theta }{2g{\left(3{\mu }_k\cos \theta -\sin \theta \right)}^2}{\omega }_0^2{R}^2+\frac{3}{4g\sin \theta }{\left(\frac{{\mu }_k\cos \theta -\sin \theta }{3{\mu }_k\cos \theta -\sin \theta }{\omega }_{0}R\right)}^2\\ x_2=\frac{{\mu }_k\cos \theta -\sin \theta }{4g\sin \theta \left(3{\mu }_k\cos \theta -\sin \theta \right)}{\omega }_0^2{R}^2\end{array}}$

Referencias

Basta, Di Gennaro, Piccciarelli. A desktop apparatus for studying rolling motion. Phys. Educ. 34 (6) November 1999, pp. 371-375

Carvalho P. S., Sampaio e Sousa A. An inexpensive technique to measure coefficients of friction with rolling solids. The Physics Teacher, Vol 43, November 2005, pp. 548-550

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Ejemplo 30, enunciado, 167, solución, 184-185

Roseli Constantino Schwerz, Adriana da Silva Fontes, Andre Luis Schwerz. Rolling with Slipping and Transition to Pure Rolling on an Inclined Plane. The Physics Teacher, Vol. 62, February 2024, pp. 132-134