Equilibrio y estabilidad

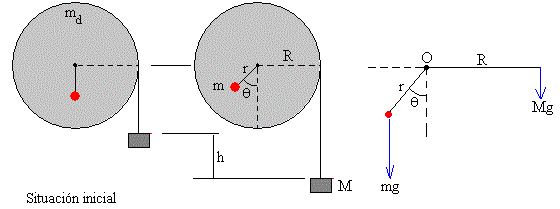
El equilibrio se logra, cuando el momento del peso que cuelga respecto del eje de rotación del disco, es igual y de sentido contrario al momento de la masa adicional m pegada al disco a una distancia r de su eje. El desplazamiento angular de equilibrio θ_e  de la masa puntual es

MgR=mgr·sinθ_e

${\displaystyle \text{sin}{\theta }_e=\frac{MR}{mr}}$

La altura de equilibrio del bloque es h_e=R·θ_e

El ángulo θ_e existe si se cumple que MR≤mr

Energía potencial

Consideremos la situación cuando la masa adicional m se ha desplazado un ángulo θ, y el bloque de masa M ha descendido una altura h=R·θ (véase la primera figura)

E_p(θ)=mgr(1-cosθ)-MgR·θ.

Representamos la energía potencial en el intervalo (0, 3π) para los siguientes valores:

• La masa puntual sobre el disco, m=0.7 kg
• La masa del bloque que cuelga M=0.2 kg
• La distancia de la masa puntual pegada al disco al eje del disco, r=0.5 m
• El radio del disco, R=1 m

M=0.2; %bloque
m=0.7; %masa puntual sobre el disco
R=1; %radio del disco
r=0.5; %posición de la masa puntual

f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
fplot(f,[0,3*pi])
set(gca,'XTick',0:pi/2:3*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi'})
grid on
xlabel('\theta')
ylabel('E_p')
title('Energía potencial')

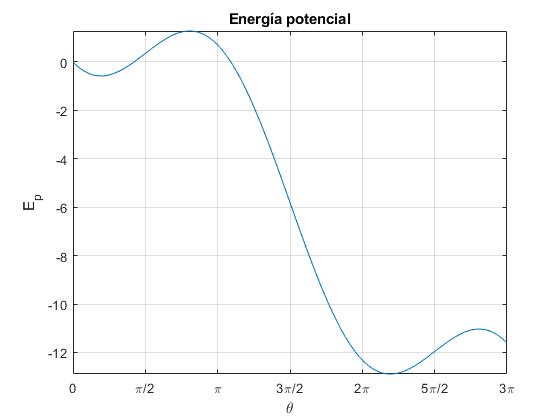
El intervalo (0,π), es la región de interés en la que vamos a analizar este sistema mecánico

• Para MR<mr

Representamos la energía potencial en el intervalo (0,π) para los siguientes valores:

• La masa puntual sobre el disco, m=0.5 kg
• La masa del bloque que cuelga, M=0.2 kg
• La distancia de la masa puntual pegada al disco al eje del disco, r=0.5 m
• El radio del disco, R=1 m

M=0.2; %bloque
m=0.5; %masa puntual sobre el disco
R=1; %radio del disco
r=0.5; %distancia al eje de la masa puntual

f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
fplot(f,[0,pi])
ylim([-1.2,0])
%máximo y mínimo
th=asin(M*R/(m*r));
line([th,th],[-1.2,f(th)], 'lineStyle','--','color','k')
line([pi-th,pi-th],[-1.2,f(pi-th)], 'lineStyle','--','color','k')

%movimientos
line([0,pi],[-0.4,-0.4], 'color','b')
g=@(x) f(x)+0.4;
ang=fzero(g,pi/8);
line([ang,ang],[-1.2,f(ang)],'lineStyle','--','color','b')
line([0,pi],[-0.6,-0.6], 'color','r')
g=@(x) f(x)+0.6;
ang=fzero(g,pi/8);
line([ang,ang],[-1.2,f(ang)],'lineStyle','--','color','r')
ang=fzero(g,pi/2);
line([ang,ang],[-1.2,f(ang)],'lineStyle','--','color','r')
set(gca,'XTick',0:pi/4:pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
grid on
xlabel('\theta')
ylabel('E_p')
title('Energía potencial')



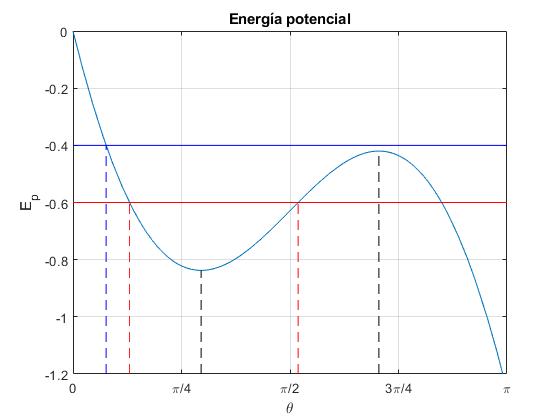
Calculamos sus extremos derivando la función energía potencial E_p(θ) respecto del ángulo θ, e igualando a cero.

${\displaystyle \frac{d{E}_p}{d\theta }=mgr\sin \theta -MgR=0\text{sin}{\theta }_e=\frac{MR}{mr}}$

hay dos posibles ángulos, θ_e y π-θ_e. Vamos a comprobar que al primero le corresponde un mínimo de la energía potencial, mientras que al segundo le corresponde un máximo. Hallamos la derivada segunda de la función energía potencial

${\displaystyle \frac{d^2{E}_p}{d{\theta }^2}=mgr\text{cos}\theta }$

El coseno es positivo (mínimo) para θ_e, y negativo (máximo) para π-θ_e. En la figura, vemos que la función E_p(θ) presenta un mínimo para θ_e=53°, y un máximo para 180- θ_e=127°. Líneas a trazos de color negro en la figura

Cuando la energía del sistema es E=-0.4 J, el dispositivo se puede mover desde la posición θ₁=13.7°, (en color azul en la figura) raíz de la ecuación transcendente

E=mgr(1-cosθ)-MgR·θ

>> f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
>> g=@(x) f(x)+0.4;
>> fzero(g,pi/8)*180/pi
ans =   13.7436

Cuando la energía del sistema es E=-0.6 J, el dispositivo se puede mover desde la posición θ₁=23.5°, hasta la posición θ₂=93.3° (en color rojo en la figura) raíces de dicha ecuación transcendente

>> f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
>> g=@(x) f(x)+0.6;
>> fzero(g,pi/8)*180/pi
ans =   23.4595
>> fzero(g,pi/2)*180/pi
ans =   93.3727

• Para MR=mr

El máximo y el mínimo coinciden en θ=90° que es el punto de inflexión.

• Para MR>mr

La función energía potencial es una función decreciente de θ.

M=0.3; %bloque
m=0.5; %masa puntual sobre el disco
R=1; %radio del disco
r=0.5; %distancia al eje de la masa puntual

f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
fplot(f,[0,pi])
ylim([-4,0])
%movimientos
g=@(x) f(x)+0.6;
ang=fzero(g,pi/8);
line([ang,ang],[-4,f(ang)],'lineStyle','--','color','b')
line([0,pi],[-0.6,-0.6], 'color','r')
set(gca,'XTick',0:pi/4:pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
grid on
xlabel('\theta')
ylabel('E_p')
title('Energía potencial')



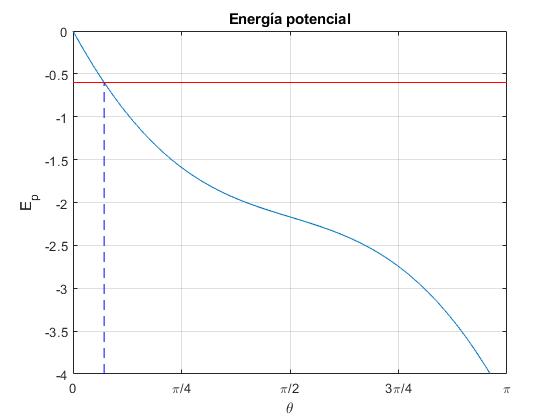
Una partícula cuya energía E=-0.6 J se mueve desde la posición angular θ₁=13° en adelante

Hay dos posibles movimientos:

• Se parte de una posición inicial θ₁ en reposo y la posición θ crece indefinidamente. El bloque cae sin detenerse

• Se parte de una posición inicial θ₁ en reposo y se llega a una posición θ₂ en reposo, el movimiento se repite entre estas dos posiciones alrededor de la posición de equilibrio θ_e

Ecuación del movimiento

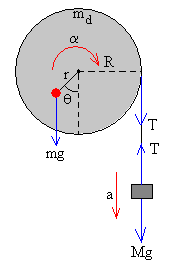
En la figura, se muestran las fuerzas que actúan sobre el disco y las fuerzas que actúan sobre el bloque de masa M. El disco gira en el sentido indicado con aceleración angular α, y el bloque lleva una aceleración a. La relación entre ambas aceleraciones es  a=α·R

• Ecuación del movimiento del bloque

Mg-T=Ma

• Ecuación del movimiento del disco y la masa puntual m

Iα=T·R-mgr·sinθ

El momento de inercia del disco de masa m_d y de la masa adicional m es

${\displaystyle I=\frac{1}{2}{m}_d{R}^2+m{r}^2}$

Eliminando la tensión T de la cuerda, llegamos a la ecuación diferencial del movimiento del disco

${\displaystyle \left(\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2\right)\frac{d^2\theta }{d{t}^2}=MgR-mgr\sin \theta }$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales t=0, θ=θ₁, dθ/dt=0. Dónde θ₁ es la posición de partida que hemos calculado en el apartado anterior

Analizamos los dos posibles movimientos:

• Se parte de una posición inicial θ₁ en reposo y la posición θ crece indefinidamente. El bloque cae sin detenerse

Creamos la función stop_atwood para detener el procedimiento de integración de la ecuación diferencial cuando la posición θ=3π

function [value,isterminal,direction]=stop_atwood(t,x)
   %x(1) es  x, x(3) es y
    value=x(1)-3*pi;
    isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
    direction=1; % 1 crece, -1 decrece, 0 no importa
end

Para la energía E=-0.4 J, calculamos la posición θ₁ de partida en reposo y resolvemos la ecuación diferencial, representando la posición θ y la velocidad dθ/dt en función del tiempo t

M=0.2; %bloque
m=0.5; %masa puntual sobre el disco
R=1; %radio del disco
r=0.5; %distancia al eje de la masa puntual
md=1; %masa del disco
energia=-0.4;

%posición de partida en reposo
f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x)-energia;
ang=fzero(f,pi/8);

%movimiento
f=@(t,x) [x(2); (M*9.8*R-m*9.8*r*sin(x(1)))/(md*R^2/2+m*r^2+M*R^2)]; 
opts=odeset('events',@stop_atwood);
[t,x]=ode45(f,[0,30],[ang,0], opts);

subplot(2,1,1)
plot(t,x(:,1)) 
set(gca,'YTick',0:pi/2:3*pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi'})
grid on
xlabel('t')
ylabel('\theta');
title('Posición')
subplot(2,1,2)
plot(t,x(:,2)) 
grid on
xlabel('t')
ylabel('d\theta/dt');
title('Velocidad')



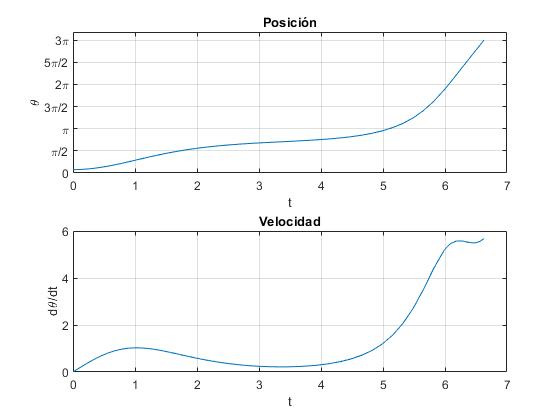
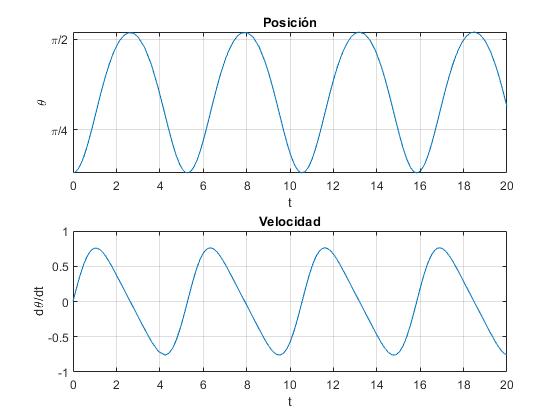
• Se parte de una posición inicial θ₁ en reposo y se llega a una posición θ₂ en reposo, el movimiento se repite entre estas dos posiciones alrededor de la posición de equilibrio θ_e

Para la energía E=-0.6 J, calculamos la posición θ₁ de partida en reposo y resolvemos la ecuación diferencial, representando la posición θ y la velocidad dθ/dt en función del tiempo t

M=0.2; %bloque
m=0.5; %masa puntual sobre el disco
R=1; %radio del disco
r=0.5; %distancia al eje de la masa puntual
md=1; %masa del disco
energia=-0.6;

%posición de partida en reposo
f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x)-energia;
ang=fzero(f,pi/8);

%movimiento
f=@(t,x) [x(2); (M*9.8*R-m*9.8*r*sin(x(1)))/(md*R^2/2+m*r^2+M*R^2)]; 
[t,x]=ode45(f,[0,20],[ang,0]);

subplot(2,1,1)
plot(t,x(:,1)) 
set(gca,'YTick',0:pi/4:pi)
set(gca,'YTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
grid on
xlabel('t')
ylabel('\theta');
title('Posición')
subplot(2,1,2)
plot(t,x(:,2)) 
grid on
xlabel('t')
ylabel('d\theta/dt');
title('Velocidad')

Oscilaciones alrededor de la posición de equilibrio estable

Como caso particular, estudiamos las oscilaciones de pequeña amplitud, alrededor de la posición de equilibrio θ_e

Poniendo θ=θ_e+φ, en la ecuación diferencial

${\displaystyle \left(\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2\right)\frac{d^2\phi }{d{t}^2}=MgR-mgr\sin \text{(}\phi +{\theta }_e)}$

Desarrollando el seno de una suma, y aproximando sinφ≈φ, cosφ≈1

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2\right)\frac{d^2\phi }{d{t}^2}=-mgr\cos {\theta }_e·\phi \\ \frac{d^2\phi }{d{t}^2}+\frac{mgr\cos {\theta }_e}{\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2}\phi =0\end{array}}$

Que es la ecuación diferencial de un MAS de frecuencia angular

${\displaystyle {\omega }^2=\frac{mgr\cos {\theta }_e}{\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2}P=2\pi \sqrt{\frac{\frac{1}{2}{m}_d{R}^2+m{r}^2+M{R}^2}{g\sqrt{m^2{r}^2-M^2{R}^2}}}}$

Ejemplo:

• Masa del disco, m_d=1 kg
• Masa puntual pegada al disco, m=0.3 kg
• Masa del bloque que cuelga, M=0.1 kg
• Radio del disco R=1 m
• Distancia de la masa puntual m al centro del disco, r=0.5 m

Ángulos máximo y mínimo

${\displaystyle \sin {\theta }_e=\frac{0.1·1}{0.3·0.5}}$

La función energía potencial presenta un mínimo para θ_e=41.8°, y un máximo para 180- θ_e=138.2°

>> asin(M*R/(m*r))*180/pi
ans =   41.8103

El periodo de las oscilaciones de pequeña amplitud alrededor de la posición de equilibrio estable es

${\displaystyle P=2\pi \sqrt{\frac{\frac{1}{2}1·1^2+0.3·{0.5}^2+0.1·1^2}{9.8\sqrt{{0.3}^2·{0.5}^2-{0.1}^2·1^2}}}=4.93\text{s}}$

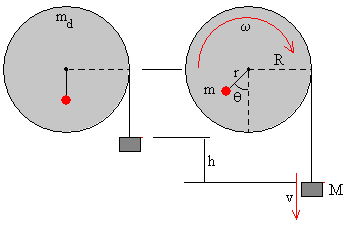
En el programa interactivo, el sistema parte del reposo desde la posición θ=0. La energía inicial es cero. Cuando se encuentra en la posición θ=60°=π/3, la energía potencial vale

E_p=0.3·9.8·0.5(1-cos(π/3))-0.1·9.8·1.0·(π/3)=-0.29 J

La energía cinética es la suma de la energía cinética de rotación del disco que se mueve con velocidad angular ω, y la energía cinética del bloque que se mueve con velocidad v. La relación entre ambas velocidades es v= ω·R

Aplicando el principio de conservación de la energía

E_k+E_p=0,

0.3375ω²-0.29=0, ω=0.93 rad/s

La energía potencial vuelve a ser cero en la posición

E_p(θ)=mgr(1-cosθ)-MgR·θ=0. El ángulo θ, se obtiene resolviendo la ecuación transcendente

mr(1-cosθ)-MR·θ=0
1.5(1-cosθ)-θ=0

La raíz es θ=1.71 rad=98°.

>> f=@(x) 9.8*(m*r*(1-cos(x))-M*R*x);
>> fzero(f,pi/2)*180/pi
ans =   98.1964

Sistemas análogos

Escribiendo la energía potencial en forma V(θ) dependiente del parámetro adimensional A, describimos otros sistemas análogos, por ejemplo, el sistema magneto-mecánico consistente en un cilindro con un imán en su interior que rueda sin deslizar a la largo de un plano inclinado en en una región en la que existe un campo magnético uniforme cuya dirección es vertical

${\displaystyle \begin{array}{l}{E}_p(\theta )=mgr(1-\cos \theta )-MgR\theta \hfill \\ V(\theta )=A(1-\cos \theta )-\theta \hfill \end{array}}$

Calculamos los extremos de esta función

${\displaystyle \begin{array}{l}\frac{dV}{d\theta }=A\sin (\theta )-1=0 \hfill \\ \frac{d^{2}V}{d{\theta }^2}=A\cos (\theta )\hfill \end{array}}$

Son máximos cuando la derivada segunda es negativa y son mínimos cuando la derivada segunda es positiva. Llamando φ=arcsin(1/A), con A≥1.

• Los máximos se producen para θ_n=φ+2nπ
• Los mínimos para θ_n= π-φ+2nπ

En los extremos (máximos y mínimos) el momento neto que actúa sobre el sistema es cero. Estas son las posiciones de equilibrio: estable en los mínimos e inestable en los máximos.

A=3; %parámetro
f=@(x) A*(1-cos(x))-x;
hold on
fplot(f, [-10,10])
z=asin(1/A);
for n=-1:1
%mínimos
    plot(z+n*2*pi,f(z+n*2*pi),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
%máximos
    plot(pi-z+n*2*pi,f(pi-z+n*2*pi),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
end
hold off
grid on
set(gca,'XTick',-2*pi:pi:2*pi)
set(gca,'XTickLabel',{'-2\pi','-\pi','0','\pi','2\pi'})
xlabel('\theta')
ylabel('V(\theta)')
title('Energía potencial')

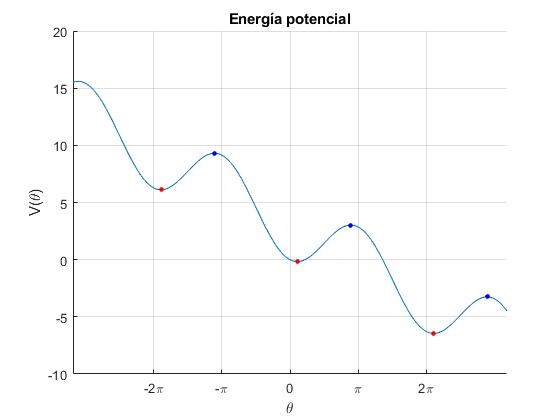
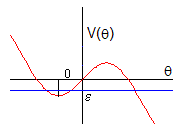
La representación gráfica de V(θ), nos permite describir cualitativamente el movimiento del sistema para una energía total ε dada.

El código para representar una parte de la figura es

function atwood_1
    A=3; %parámetro
    E=7; %energía 
    f=@(x) A*(1-cos(x))-x;
    fm=@(x) f(x)-E;
    x=linspace(-10,10,20);
    r=raices(fm,x);
    hold on
    fplot(f, [-10,10])
    line([-10,10],[E,E],'color','k');
%dibuja las raíces
    ordenada=ones(1,length(r))*E;
    plot(r, ordenada,'ro','markersize',4,'markerfacecolor','r')
    hold off
    %grid on
    xlabel('\theta')
    ylabel('V(\theta)')
    title('Energía potencial')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

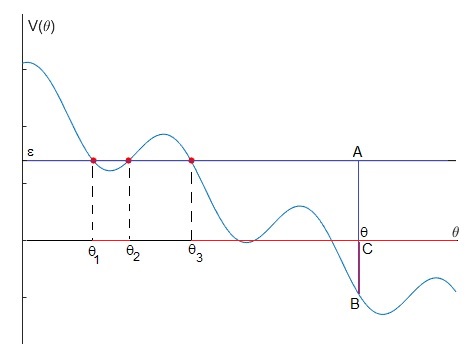
Como se aprecia en la figura, para la energía total ε hay dos regiones en las que se pueden mover el sistema, aquellas en las que su energía cinética es positiva o bien aquellas en las que la energía total ε es mayor que la energía potencial V(θ). La condición ε≥V(θ), se cumple para las posiciones angulares θ en el segmento θ₁≤θ≤θ₂ y para θ≥θ₃ (señaladas en color rojo en la figura). Siendo θ₁, θ₂ y θ₃ las raíces de la ecuación trascendente ε=V(θ) calculadas mediante la función raices.

La posición inicial determina la región en la que se moverá posteriormente. Imaginemos que esta posición es θ>θ₃, señalada en la figura. Su energía potencial es el segmento CB, la energía total es el segmento CA, luego la energía cinética es el segmento AB. El punto de intersección θ₃ entre la recta y la curva de energía potencial, ε=V(θ) señala el punto de retorno, es decir, aquél en el que la velocidad es nula.

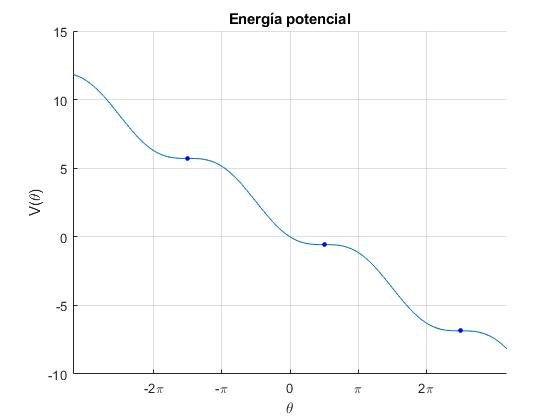
Cuando A=1, no hay máximos ni mínimos locales, son puntos de inflexión ya que la primera y segunda derivadas son nulas en dichos puntos. dV/dθ=0, y d²V/dθ²=0.

A=1;
f=@(x) A*(1-cos(x))-x;
hold on
fplot(f, [-10,10])
z=asin(1/A);
for n=-1:1
%mínimos
    plot(z+n*2*pi,f(z+n*2*pi),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
%máximos
    plot(pi-z+n*2*pi,f(pi-z+n*2*pi),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
end
hold off
grid on
set(gca,'XTick',-2*pi:pi:2*pi)
set(gca,'XTickLabel',{'-2\pi','-\pi','0','\pi','2\pi'})
xlabel('\theta')
ylabel('V(\theta)')
title('Energía potencial')

Ecuación del movimiento

Escribimos la ecuación diferencial del movimiento de la forma

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=\frac{MgR}{I_0}\left(1-\frac{mr}{MR}\sin \theta \right)\\ \frac{d^2\theta }{d{t}^2}=C\left(1-A\sin \theta \right)\end{array}}$

Se resuelve la ecuación diferencial mediante el procedimiento numéricos con las condiciones iniciales θ=θ₀ y dθ/dt=0 en el instante t=0, siendo θ₀ un punto de retorno o una de las raíces de la ecuación trascendente ε=V(θ).

El comportamiento del sistema viene determinado por el parámetro A, ya que el parámetro C actúa de factor de escala.

1. Cuando A>1 se pueden dar dos comportamientos

• Oscila entre dos posiciones angulares θ₁≤θ≤θ₂.

• Se mueve sin límite, θ≥θ₃

2. Para A≤1 el movimiento sin límite, θ≥θ₃.

function atwood_3
    A=3; %parámetro
    E=7; %energía 
    f=@(x) A*(1-cos(x))-x;
    fm=@(x) f(x)-E;
    x=linspace(-10,10,20);
    r=raices(fm,x);
    x0=[r(1),0]; %posición inicial, cambiar a otro índice 2 ó 3
    f=@(t,x) [x(2); 1-A*sin(x(1))]; 
    [t,x]=ode45(f,[0 10],x0);
    plot(t,x(:,1))
    grid on
    xlabel('t')
    ylabel('\theta');
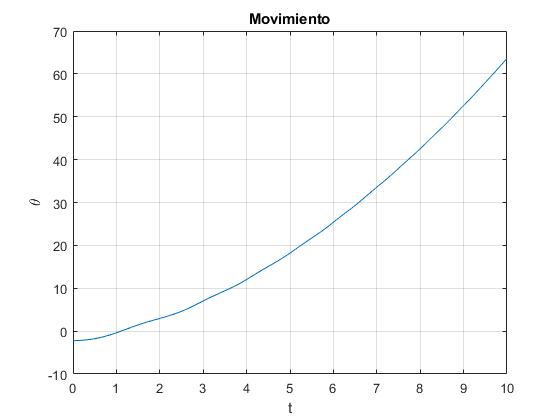
    title('Movimiento')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

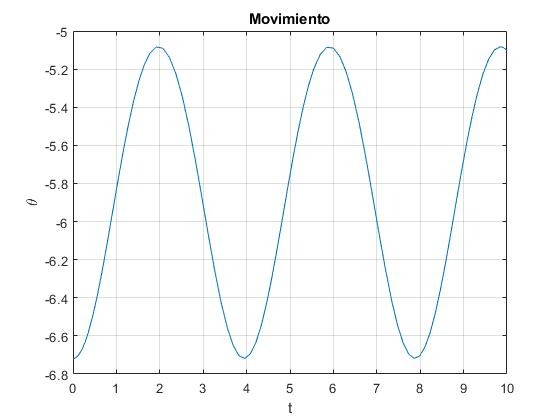
Si elegimos la posición inicial la tercera raíz, el movimiento es θ≥θ₃

Oscilaciones de pequeña amplitud alrededor de una posición de equilibrio

Si desarrollamos en serie la función f(θ)=C(1-Asin(θ)), alrededor de la posición de equilibrio (mínimo de la energía potencial) θ₀=arcsin(1/A) con A>1.

${\displaystyle \begin{array}{l}f(\theta )=f({\theta }_0)+{\left(\frac{df}{dz}\right)}_{{\theta }_0}(\theta -{\theta }_0)+\mathrm{...}\hfill \\ f(\theta )\approx -CA\cos ({\theta }_0)(\theta -{\theta }_0)=-C\sqrt{A^2-1}(\theta -{\theta }_0)\hfill \end{array}}$

La ecuación del movimiento se transforma en la ecuación diferencial de un M.A.S.

${\displaystyle \frac{d^2\phi }{d{t}^2}+{\omega }^2\phi =0\phi =\theta -{\theta }_0}$

La frecuencia angular ω del M.A.S. es

${\displaystyle \omega =\sqrt{C\sqrt{A^2-1}}}$

Actividades

Se introduce

• La masa puntual m, en el control titulado Masa izquierda
• La masa del bloque que cuelga M, en el control titulado Masa derecha
• La distancia r de la masa puntual m pegada al disco al eje del disco, en el control titulado Posición
• El radio del disco se ha fijado en R=1 m
• La masa del disco se ha fijado en m_d=1 kg

Se pulsa el botón titulado Nuevo

Se dibuja la función energía potencial, observamos el máximo y el mínimo si existen.

A la derecha, observamos el movimiento del sistema, que oscila alrededor de la posición del mínimo de energía potencial si existe, o el bloque cae si no existe posición de equilibrio estable.

Referencias

M Fiolhais, B Golli, R Nogueira. Mechanical apparatus for the fold catastrophe demonstration. Eur. J. Phys. 42 (2021) 045001

Manuel Fiolhais, Rogério Nogueira. Sistema mecánico con un potencial catastrófico. Revista Española de Física, 34-1, Enero-marzo 2020, págs. 30-33

Greenslade T. B. “Atwood’s” oscillator. Am. J. Phys. 56 (12) December 1988, pp. 1151-1153