Sean dos movimientos ondulatorios cuya forma viene descrita por la función f(x)

${\displaystyle \begin{array}{l}\{\begin{array}{l}{y}_1(x,t)=f\left(\left(x-x_0\right)-v\left(t-t_0\right)\right)\\ y_2(x,t)=f\left(\left(x-x_0\right)+v\left(t-t_0\right)\right)\end{array}\\ y(x,t)=y_1(x,t)-y_2(x,t)\end{array}}$

• y₁(x,t) describe el movimiento de un pulso que se propaga a lo largo del eje X hacia la derecha con velocidad v
• y₂(x,t) describe el movimiento de un pulso que se propaga a lo largo del eje X hacia la izquierda con velocidad v
• y(x,t) es la interferencia destructiva de los dos pulsos que se anula en el instante t₀

${\displaystyle y(x,t_0)=y_1(x,t_0)-y_2(x,t_0)=f\left(x-x_0\right)-f\left(x-x_0\right)=0}$

La densidad de energía cinética (J/m) es

${\displaystyle u_k(x,t)=\frac{1}{2}\rho {\left(\frac{\partial y}{\partial t}\right)}^2}$

donde ρ es la densidad lineal (kg/m) de la cuerda

La densidad de energía potencial es

${\displaystyle u_p(x,t)=\frac{1}{2}\rho v^2{\left(\frac{\partial y}{\partial x}\right)}^2}$

Interferencia destructiva

Estudiamos la interferencia destructiva de dos pulsos iguales

${\displaystyle \begin{array}{l}\{\begin{array}{l}{y}_1(x,t)=\frac{b^3}{b^2+{\left(x-v\left(t-\frac{3}{v}\right)\right)}^2}=\frac{b^3}{b^2+{\left(x-vt+3\right)}^2}\\ y_2(x,t)=\frac{b^3}{b^2+{\left(x+v\left(t-\frac{3}{v}\right)\right)}^2}=\frac{b^3}{b^2+{\left(x+vt-3\right)}^2}\end{array}\\ y(x,t)=y_1(x,t)-y_2(x,t)=b^3\left\{\frac{1}{b^2+{\left(x-vt+3\right)}^2}-\frac{1}{b^2+{\left(x+vt-3\right)}^2}\right\}\end{array}}$

Representamos los dos pulsos y su superposición en el instante t=3.5.

v=1;
b=1;
t=3.5;
y1=@(x) b^3./(b^2+(x-v*t+3).^2);
y2=@(x) -b^3./(b^2+(x+v*t-3).^2);
hold on
fplot(y1,[-10,10], 'lineStyle','--')
fplot(y2,[-10,10], 'lineStyle','--')
fplot(@(x) y1(x)+y2(x),[-10,10],'color','k')
hold off
grid on
ylim([-1.1,1.1])
xlabel('x')
ylabel('y_1+y_2')
title(sprintf('Superposición, t=%1.1f',t))

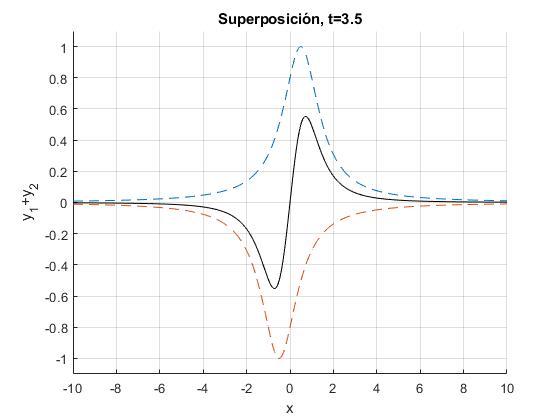
y(x,t)=0 en el instante t=3/v, desaparecen los pulsos

${\displaystyle y\left(x,\frac{3}{v}\right)=\frac{b^3}{b^2+x^2}-\frac{b^3}{b^2+x^2}=0}$

Actividades

En la animación se muestra

• Los dos pulsos, en color azul y rojo, líneas discontínuas
• La superposición de los dos pulsos y(x,t) en color negro, línea gruesa

Densidad de energía cinética

${\displaystyle \begin{array}{l}\frac{\partial y}{\partial t}=2b^{3}v\left\{\frac{x-vt+3}{{\left(b^2+{\left(x-vt+3\right)}^2\right)}^2}+\frac{x+vt-3}{{\left(b^2+{\left(x+vt-3\right)}^2\right)}^2}\right\}\\ u_k(x,t)=\frac{1}{2}\rho {\left(\frac{\partial y}{\partial t}\right)}^2\end{array}}$

Representamos la velocidad $\frac{\partial y}{\partial t}$ de desplazamiento de las partículas de la cuerda, mediante flechas en función de x para el instante t=0. La curva de color rojo es la densidad de energía cinética

b=1; %parámetro
v=1;%velocidad
lambda=1; %densidad lineal

t=0; %instante
hold on
g=@(x) 2*v*b^3*((x-v*t+3)./(b^2+(x-v*t+3).^2).^2+(x+v*t-3).
/(b^2+(x+v*t-3).^2).^2);
x1=linspace(-10,10,50);
quiver(x1,zeros(1,length(x1)), zeros(1,length(x1)), g(x1))
e_k=@(x) lambda*g(x).^2/2;
fplot(e_k,[-10,10],'color','r') %energía cinética
hold off
grid on
xlim([-10,10])
xlabel('x')
ylabel('y,e_k, e_p')
title('Energía cinética, t=0')

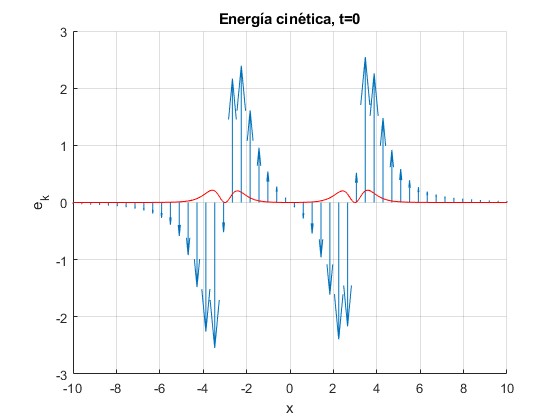
Mediante la función solve determinamos las abscisas de los puntos de la cuerda que permanecen estacionarios en el instante t=0

>> syms v b x t;
>> dy=2*v*b^3*((x-v*t+3)/(b^2+(x-v*t+3)^2)^2+(x+v*t-3)/(b^2+(x+v*t-3)^2)^2);
>> dyy=subs(dy,{v,b,t},{1,1,0});
>> solve(dyy)
ans =
                 0
 (- 6*10^(1/2) - 10)^(1/2)
   (6*10^(1/2) - 10)^(1/2)
-(- 6*10^(1/2) - 10)^(1/2)
  -(6*10^(1/2) - 10)^(1/2)
>> double(ans)
ans =
   0.0000 + 0.0000i
   0.0000 + 5.3827i
   2.9956 + 0.0000i
   0.0000 - 5.3827i

Las tres abscisas son x=0, 2.9956, -2.9956, tal como se aprecia en la figura

Cambiamos el tiempo t=3, cuando desaparecen los pulsos

${\displaystyle u_k\left(x,\frac{3}{v}\right)=\frac{1}{2}\rho {\left\{4v{b}^3\frac{x}{{\left(b^2+x^2\right)}^2}\right\}}^2=8\rho v^2{b}^6\frac{x^2}{{\left(b^2+x^2\right)}^4}}$

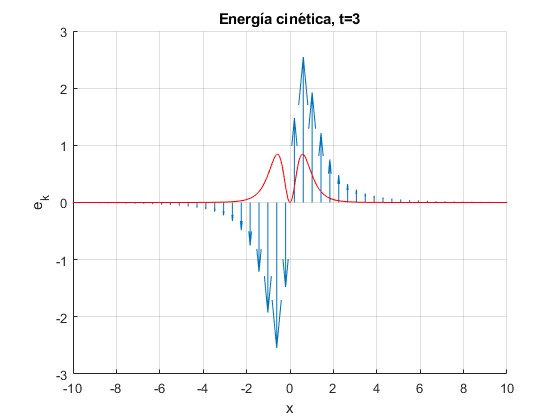
Los extremos (dos máximos y un mínimo) en las posiciones

${\displaystyle \begin{array}{l}\frac{d}{dx}\left(\frac{x^2}{{\left(b^2+x^2\right)}^4}\right)=\frac{2x{\left(b^2+x^2\right)}^4-x^{2}4·2x{\left(b^2+x^2\right)}^3}{{\left(b^2+x^2\right)}^8}=0\\ {\left(b^2+x^2\right)}^{3}x\left(b^2-3x^2\right)=\mathrm{0,}\{\begin{array}{l}x=0\\ x=\pm \frac{b}{\sqrt{3}}\end{array}\end{array}}$

El máximo de la densidad de energía cinética vale

${\displaystyle e_k=\frac{27}{32}\rho v^2}$

La energía cinética de la cuerda de extensión infinita en el instante t

${\displaystyle E_k={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{u}_k(x,t)·dx=\frac{1}{2}\rho }{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left(\frac{\partial y}{\partial t}\right)}^{2}dx}}$

Calcularemos esta integral por procedimientos numéricos empleando la función integral

Densidad de energía potencial

${\displaystyle \begin{array}{l}\frac{\partial y}{\partial x}=2b^3\left\{-\frac{x-vt+3}{{\left(b^2+{\left(x-vt+3\right)}^2\right)}^2}+\frac{x+vt-3}{{\left(b^2+{\left(x+vt-3\right)}^2\right)}^2}\right\}\\ u_p(x,t)=\frac{1}{2}\rho v^2{\left(\frac{\partial y}{\partial x}\right)}^2\end{array}}$

La densidad de energía potencial es nula para t=3/v cuando el desplazamiento y(t,3/v)=0.

b=1; %parámetro
v=1;%velocidad
lambda=1; %densidad lineal

t=0; %instante
f=@(x) b^3*(1./(b^2+(x-v*t+3).^2)-1./(b^2+(x+v*t-3).^2));
hold on
fplot(f,[-10,10],'color','k','lineWidth',1.5) %pulso
h=@(x) 2*b^3*(-(x-v*t+3)./(b^2+(x-v*t+3).^2).^2+(x+v*t-3).
/(b^2+(x+v*t-3).^2).^2);
e_p=@(x) lambda*v^2*h(x).^2/2;
fplot(e_p,[-10,10],'color','b') %energía potencial
hold off
grid on
xlabel('x')
ylabel('y, e_p')
title('Energía potencial, t=0')

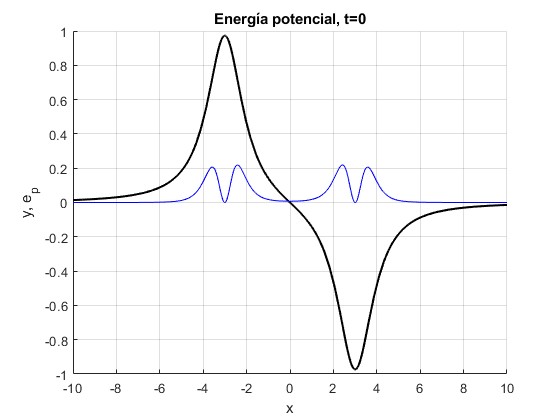
Mediante la función solve determinamos las abscisas de los puntos de la cuerda que cuyo desplazamiento y(x,t) es máximo (mínimo), en el instante t=0

>> syms x t b v;
>> >> dy=-(x-v*t+3)/(b^2+(x-v*t+3)^2)^2+(x+v*t-3)/(b^2+(x+v*t-3)^2)^2;
>> dyy=subs(dy,{t,b,v},{0,1,1});
>> solve(dyy)
ans =
 (8/3 - (2*91^(1/2))/3)^(1/2)
 ((2*91^(1/2))/3 + 8/3)^(1/2)
-(8/3 - (2*91^(1/2))/3)^(1/2)
-((2*91^(1/2))/3 + 8/3)^(1/2)
>> double(ans)
ans =
   0.0000 + 1.9217i
   3.0044 + 0.0000i
   0.0000 - 1.9217i
  -3.0044 + 0.0000i

Las dos abscisas son x=-3.0, 3.0, tal como se aprecia en la figura

La energía potencial de la cuerda de extensión infinita en el instante t

${\displaystyle E_p={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{u}_p(x,t)·dx=\frac{1}{2}\rho v^2}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left(\frac{\partial y}{\partial x}\right)}^{2}dx}}$

Calcularemos esta integral por procedimientos numéricos empleando la función integral

La energía cinética y potencial de la cuerda tienden hacia un valor constante cuando los pulsos se alejan uno del otro

Resultados

Representamos

• La superposición de los dos pulsos y(x,t) en color negro, línea gruesa
• La densidad de energía cinética u_k(x,t), en color rojo
• La densidad de energía potencial u_k(x,t), en color azul
• Calculamos la energía cinética E_k y la potencial E_p de la cuerda en el instante t

Los datos son

• Parámetro, b=1
• Velocidad de propagación, v=1
• Densidad lineal de la cuerda, ρ=1

b=1; %parámetro
v=1;%velocidad
lambda=1; %densidad lineal

t=0; %instante
f=@(x) b^3*(1./(b^2+(x-v*t+3).^2)-1./(b^2+(x+v*t-3).^2));
hold on
fplot(f,[-10,10],'color','k','lineWidth',1.5) %pulso
g=@(x) 2*v*b^3*((x-v*t+3)./(b^2+(x-v*t+3).^2).^2+(x+v*t-3).
/(b^2+(x+v*t-3).^2).^2);
e_k=@(x) lambda*g(x).^2/2;
fplot(e_k,[-10,10],'color','r') %energía cinética
h=@(x) 2*b^3*(-(x-v*t+3)./(b^2+(x-v*t+3).^2).^2+(x+v*t-3)./
(b^2+(x+v*t-3).^2).^2);
e_p=@(x) lambda*v^2*h(x).^2/2;
fplot(e_p,[-10,10],'color','b') %energía potencial
if v*t<3  
    xf=3-v*t+10;
else
    xf=v*t-3+10;
end
e1=integral(e_p,-xf,xf);
e2=integral(e_k,-xf,xf);
disp([e1,e2])
hold off
grid on
xlabel('x')
ylabel('y,e_k, e_p')
title('Pulsos, t=0')

En los instantes

• t=0



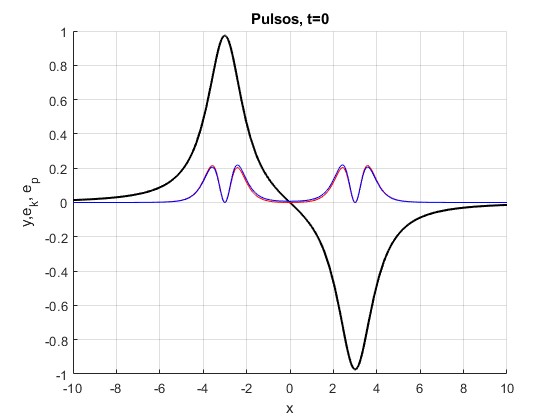
La energía potencial E_p y cinética E_k

0.8058    0.7650

• t=2



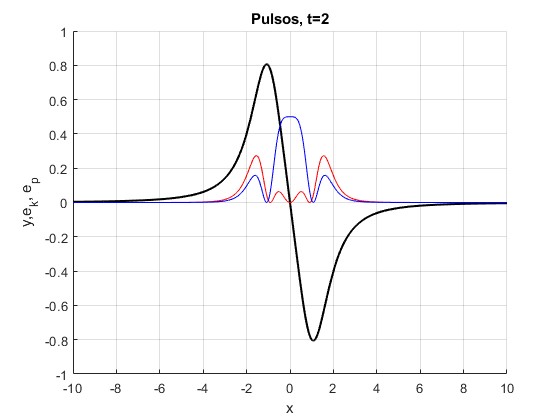
La energía potencial E_p y cinética E_k

 0.9817    0.5890

• t=3



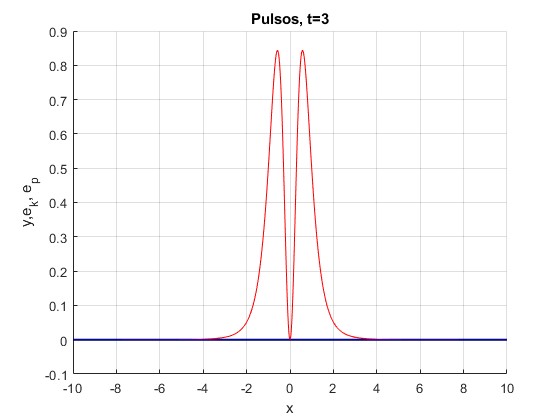
La energía potencial E_p se anula y cinética E_k

0.0000    1.5708

• t=5



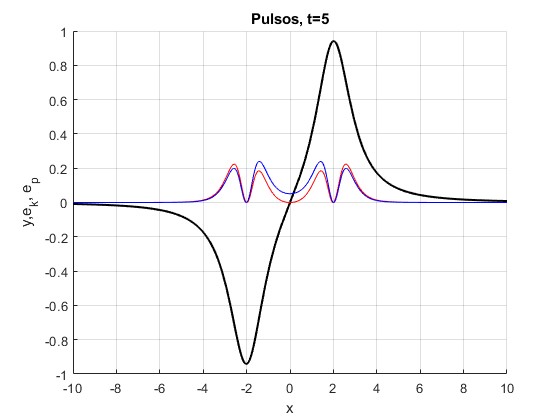
La energía potencial E_p y cinética E_k

0.8545    0.7163

Actividades

En la animación se muestra

• La superposición de los dos pulsos y(x,t) en color negro, línea gruesa
• La densidad de energía cinética u_k(x,t), en color rojo
• La densidad de energía potencial u_k(x,t), en color azul
• Representamos en forma de diagrama de tarta (esquina inferior derecha) la energía cinética E_k y la potencial E_p de la cuerda en el instante t

Observamos los cambios en la densidad de energía cinética y potencial cuando los pulsos se acercan, desaparecen (t=3/v) y se alejan uno del otro

Referencias

David Romero-Abad, Roberto Suárez-Cordova. The Energy of Two Inverted Oppositely Moving Wave Pulses: A Graphic Approach. The Physics Teacher. Vol. 62, March 2024. pp. 202-204