Oscilaciones amortiguadas por una fuerza de módulo constante (II)

Oscilaciones amortiguadas por una fuerza de módulo constante

Plano inclinado

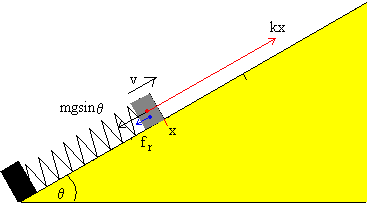
Consideremos un bloque de masa m unido a un muelle elástico de constante k que desliza a lo largo de un plano inclinado de ángulo θ. Sea μ el coeficiente de la fuerza de rozamiento entre el bloque y el plano inclinado.

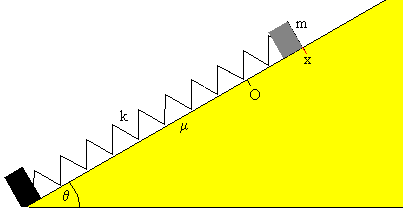
Para describir el movimiento, estableceremos el eje X a lo largo del plano, situamos el origen O en la posición del extremo libre del muelle sin deformar, tomando el sentido positivo hacia arriba.

Las fuerzas sobre el bloque son:

El peso, mg
La reacción del plano inclinado, N=mgcosθ
La fuerza que ejerce el muelle deformado, kx
La fuerza de rozamiento, f_r

El bloque desliza a lo largo del plano inclinado hacia abajo, v<0

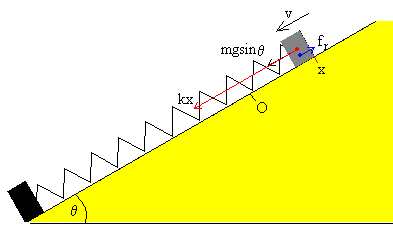
El bloque parte de la posición x₀>0 y desliza hacia abajo si la componente del peso mg·sinθ y la fuerza que ejerce el muelle kx₀ es mayor que la fuerza de rozamiento máxima, μ_s·mg·cosθ,

mgsinθ+kx₀≥μ_s·mg·cosθ

en caso contrario, permanecerá en reposo en la posición inicial. Supongamos que se cumple esta condición y el bloque desliza hacia abajo

Cuando el bloque se mueve hacia abajo (v<0), la fuerza de rozamiento es de sentido contrario a la velocidad del bloque y vale, f_r=μ_k·N. La ecuación del movimiento es

ma=-kx-mgsinθ+μ_kmgcosθ

Escribimos la ecuación del movimiento en forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} + ω^{2} x = - a_{-} \frac{d x}{d t} < 0$

con ω²=k/m y a_-= g(sinθ-μ_kcosθ)

Las ecuaciones del movimiento nos recuerdan la ecuación diferencial de un MAS, pero además tiene un término adicional.

La solución de la ecuación diferencial es la suma de la homogénea (la ecuación de un MAS) más una constante C. Introduciendo la solución particular (la constante C) en la ecuación diferencial

ω²C= -a_-, C= -a_- /ω²

La solución completa de la ecuación diferencial es

$x = A sin (ω t) + B \cos (ω t) - \frac{a_{-}}{ω^{2}} v < 0$

La velocidad del bloque es

$v = \frac{d x}{d t} = A ω \cos (ω t) - B ω \sin (ω t)$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, el bloque parte de la posición x=x₀ con velocidad inicial v=0.

x₀=B-a_- /ω²0=Aω

La posición x y la velocidad v del bloque en su movimiento a lo largo del plano inclinado, hacia abajo, es

$\begin{array}{l} x = (x_{0} + \frac{a_{-}}{ω^{2}}) cos (ω t) - \frac{a_{-}}{ω^{2}} v < 0 \\ v = - (x_{0} ω + \frac{a_{-}}{ω}) sin (ω t) \end{array}$

El máximo desplazamiento x₁ se produce cuando la velocidad es nula v=0, en el instante ttal que ωt=π. La posición del bloque en este instante es

$x_{1} = - x_{0} - \frac{2 a_{-}}{ω^{2}}$

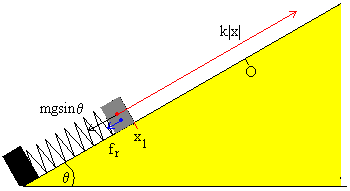
El móvil parte de x₁ con velocidad inicial nula siempre que se cumpla que

k|x₁|-mgsinθ≥ μ_smgcosθ

en caso contrario, la posición x₁será la posición final del bloque en reposo. Supongamos que se cumple la primera condición.

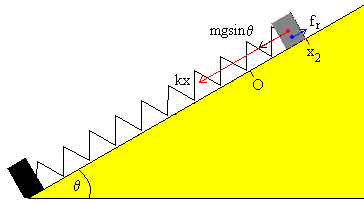
El bloque desliza a lo largo del plano inclinado hacia arriba, v>0

Cuando el bloque se mueve hacia arriba (v>0), la fuerza de rozamiento cambia de sentido y la ecuación del movimiento es

ma=-kx –mgsinθ-μ_kmgcosθ

Escribimos la ecuación del movimiento en forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} + ω^{2} x = - a_{+} \frac{d x}{d t} > 0$

con ω²=k/m y a₊= g(sinθ+μ_kcosθ)

La solución completa de la ecuación diferencial es

$x = A \sin (ω t) + B \cos (ω t) - \frac{a_{+}}{ω^{2}} v > 0$

La velocidad del bloque es

$v = \frac{d x}{d t} = A ω \cos (ω t) - B ω \sin (ω t)$

Los coeficientes A y B se determinan a partir de las condiciones iniciales. Si ponemos el contador de tiempo parcial a cero, en el instante t=0, el bloque parte de la posición x=x₁ con velocidad inicial v=0.

x₁=B-a₊ /ω²0=Aω

La posición x y la velocidad v del bloque en su movimiento a lo largo del plano inclinado, hacia arriba, es

$\begin{array}{l} x = (x_{1} + \frac{a_{+}}{ω^{2}}) cos (ω t) - \frac{a_{+}}{ω^{2}} v > 0 \\ v = - (x_{1} ω + \frac{a_{+}}{ω}) sin (ω t) \end{array}$

La velocidad del bloque es nula v=0, en el instante ttal que ωt=π, cuando la posición x₂ del bloque es

$x_{2} = - x_{1} - \frac{2 a_{+}}{ω^{2}} = x_{0} + \frac{2 a_{-} - 2 a_{+}}{ω^{2}}$

El móvil parte de x₂ con velocidad inicial nula siempre que se cumpla que

mgsinθ+kx₂≥μ_s·mg·cosθ

en caso contrario, la posición x₂ será la posición final del bloque en reposo. Supongamos que se cumple la primera condición.

Posiciones de retorno

El bloque desliza hacia abajo, después de un tiempo tal que ωt=π, la velocidad se hace cero en la posición

$x_{3} = - x_{2} - \frac{2 a_{-}}{ω^{2}} = - x_{0} + \frac{- 4 a_{-} + 2 a_{+}}{ω^{2}}$

El móvil parte de x₃ con velocidad inicial nula siempre que se cumpla que

k|x₃|-mgsinθ≥ μ_smgcosθ,

en caso contrario, la posición x₃será la posición final del bloque en reposo. Supongamos que se cumple la primera condición.

El bloque desliza hacia arriba, después de un tiempo tal que ωt=π, la velocidad se hace cero en la posición

$x_{4} = - x_{3} - \frac{2 a_{+}}{ω^{2}} = x_{0} + \frac{4 a_{-} - 4 a_{+}}{ω^{2}}$

En general, el móvil se encuentra en el instante t=(2n-1)π/ω con n=1, 2, 3..en la posición

$x_{2 n - 1} = - x_{0} + \frac{- (2 n) a_{-} + (2 n - 2) a_{+}}{ω^{2}}$

El móvil parte de x_2n-1 con velocidad inicial nula siempre que se cumpla que

k|x_2n-1|-mgsinθ≥ μ_smgcosθ,

en caso contrario, la posición x_2n-1será la posición final del bloque en reposo

El bloque se mueve hacia arriba v>0. La posición del bloque en función del tiempo es a partir del instante t=(2n-1)π/ω es

$\begin{array}{l} x = (x_{2 n - 1} + \frac{a_{+}}{ω^{2}}) cos (ω t) - \frac{a_{+}}{ω^{2}} v > 0 \\ x = (- x_{0} + \frac{- (2 n) a_{-} + (2 n - 1) a_{+}}{ω^{2}}) cos (ω t) - \frac{a_{+}}{ω^{2}} \end{array}$

El bloque se encuentra en el instante t=(2n)π/ω con n=1, 2, 3..en la posición

$x_{2 n} = x_{0} + \frac{(2 n) a_{-} - (2 n) a_{+}}{ω^{2}}$

El móvil parte de x_2n en el instante t=(2n)π/ω con velocidad inicial nula siempre que se cumpla que

mgsinθ+kx_2n≥μ_s·mg·cosθ

en caso contrario, la posición x_2nserá la posición final del bloque en reposo

El bloque se mueve hacia abajo v<0. La posición del bloque en función del tiempo es a partir del instante t=(2n)π/ω es

$\begin{array}{l} x = (x_{2 n} + \frac{a_{-}}{ω^{2}}) cos (ω t) - \frac{a_{-}}{ω^{2}} v < 0 \\ x = (x_{0} + \frac{(2 n + 1) a_{-} - (2 n) a_{+}}{ω^{2}}) cos (ω t) - \frac{a_{-}}{ω^{2}} \end{array}$

Distancia entre la posición de partida y el de llegada

La distancia entre la posición de partida x₀ y la de llegada x_2n, cuando el bloque se para definitivamente describiendo un número par (2n) de semioscilaciones es

$x_{2 n} - x_{0} = \frac{(2 n) a_{-} - (2 n) a_{+}}{ω^{2}} = (2 n) \frac{2 g μ_{k} \cos θ}{ω^{2}}$

Como el tiempo que tarda en describir una semioscilación es t=π/ω. El tiempo que tarda en pararse es t_2n=(2n)π/ω. La distancia d entre el punto de partida y el de llegada es

$d = x_{2 n} - x_{0} = \frac{2 g μ_{k} \cos θ}{2 n π^{2}} t_{2 n}^{2}$

Diseñamos una experiencia de laboratorio, en el que los resultados experimentales sean la medida de los tiempos t_2n desde que se suelta el bloque en la posición x₀ hasta que llega a la posición final x_2n en reposo y la distancia d entre estas dos posiciones para un número par de semioscilaciones.

Como la distancia d es proporcional al coeficiente cinético μ_k. Aplicamos el procedimiento de regresión lineal para obtener la pendiente de la recta de ajuste y determinar así, el valor experimental de μ_k.

Ejemplo:

Ángulo del plano inclinado, θ=30º
Masa del bloque, m=1.0 kg
Constante elástica del muelle, k=50 N/m
Coeficiente de rozamiento en bloque y el plano inclinado, μ_k=μ_s=0.3
Posición inicial de partida, x₀=0.5 m=50 cm

Las aceleraciones

a_-= g(sinθ-μ_kcosθ)=2.35 m/s
a₊= g(sinθ+μ_kcosθ)=7.45 m/s

Posiciones de retorno para las cuales la velocidad del bloque es cero

x₀=50 cm	x₁= -59.4
x₂=29.6	x₃=-39.0
x₄=9.3	x₅=-18.7
x₆=-11.1

En la figura, se muestra la gráfica de la posición x del bloque en función del tiempo t, señalándose las posiciones de retorno, aquellas en las que la velocidad del bloque es nula.

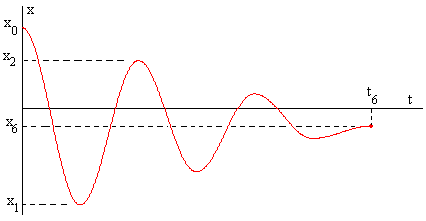
El tiempo que tarda en describir una semioscilación es π/ω=0.44 s, el tiempo total que tarda en describir 6 semioscilaciones es t₆= 2.67 s.

La distancia d entre la posición de partida y la posición final x₆ del bloque en reposo es x₆-x₀=61.11 cm.

El siguiente script calcula las posiciones de retorno en metros. El bloque parte de la posición inicial x₀=0.5 m

k=50;  m=1; mu=0.3; g=9.8; angulo=pi/6; x0=0.5;
w=sqrt(k/m);
aMenos=g*(sin(angulo)-mu*cos(angulo));
aMas=g*(sin(angulo)+mu*cos(angulo));
n=1;
while(1)
    xImpar=-x0+((-2*n)*aMenos+(2*n-2)*aMas)/w^2
    if abs(xImpar)<aMas/w^2
        break;
    end
    xPar=x0+(aMenos-aMas)*(2*n)/w^2
     if xPar<-aMenos/w^2
        break;
    end
   n=n+1;
end

xImpar =-0.5942
xPar = 0.2963
xImpar = -0.3905
xPar = 0.0926
xImpar = -0.1868
xPar = -0.1111

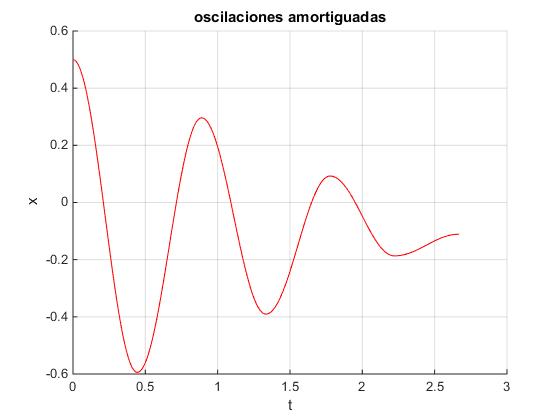
Mediante este script continuación del anterior, representamos la posición del bloque en función del tiempo hasta que se detiene

k=50;  m=1; mu=0.3; g=9.8; angulo=pi/6; x0=0.5;
w=sqrt(k/m);
aMenos=g*(sin(angulo)-mu*cos(angulo));
aMas=g*(sin(angulo)+mu*cos(angulo));

n=1;
t=linspace(0,pi/w,50);
hold on
while(1)
    x=(x0+((2*n-1)*aMenos-(2*n-2)*aMas)/w^2)*cos(w*t)-aMenos/w^2;
    plot(t,x,'r');
    xImpar=-x0+((-2*n)*aMenos+(2*n-2)*aMas)/w^2;
    if abs(xImpar)<aMas/w^2
        break;
    end
    t=t+pi/w;
     x=-(-x0+((-2*n)*aMenos+(2*n-1)*aMas)/w^2)*cos(w*t)-aMas/w^2;
    plot(t,x,'r');
    xPar=x0+(aMenos-aMas)*(2*n)/w^2;
     if xPar<-aMenos/w^2
        break;
     end
     n=n+1;
     t=t+pi/w;
end
hold off
grid on
xlabel('t')
ylabel('x')
title('oscilaciones amortiguadas')

Balance energético

El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía final y la energía inicial. La energía del sistema es la suma de

La energía cinética
La energía potencial elástica del muelle deformado
La energía potencial gravitatoria. Establecemos como nivel cero de energía potencial el origen

Si el bloque parte de la posición x₀ con velocidad v=0. La velocidad que alcanza cuando se encuentra en la posición x se calcula a partir de la ecuación

$- μ_{k} m g \cos θ | x - x_{0} | = (\frac{1}{2} k x^{2} + m g x sin θ + \frac{1}{2} m v^{2}) - (\frac{1}{2} k x_{0}^{2} + m g x_{0} sin θ)$

El bloque se detiene en la posición x₁

$- μ_{k} m g \cos θ (x_{0} - x_{1}) = (\frac{1}{2} k x_{1}^{2} + m g x_{1} sin θ) - (\frac{1}{2} k x_{0}^{2} + m g x_{0} sin θ)$

Resolvemos la ecuación de segundo grado y calculamos x₁.

$\begin{array}{l} ω^{2} x_{1}^{2} + 2 a_{-} x_{1} - ω^{2} x_{0}^{2} - 2 a_{-} x_{0} = 0 \\ x_{1} = - x_{0} - \frac{2 a_{-}}{ω^{2}} \end{array}$

Si el bloque parte de la posición x₁ con velocidad v=0. La velocidad que alcanza cuando se encuentra en la posición x se calcula a partir de la ecuación

$- μ_{k} m g \cos θ | x - x_{1} | = (\frac{1}{2} k x^{2} + m g x \sin θ + \frac{1}{2} m v^{2}) - (\frac{1}{2} k x_{1}^{2} + m g x_{1} sin θ)$

El bloque se detiene en la posición x₂

$- μ_{k} m g \cos θ (x_{2} - x_{1}) = (\frac{1}{2} k x_{2}^{2} + m g x_{2} \sin θ) - (\frac{1}{2} k x_{1}^{2} + m g x_{1} \sin θ)$

Resolvemos la ecuación de segundo grado y calculamos x₂.

$\begin{array}{l} ω^{2} x_{2}^{2} + 2 a_{+} x_{2} - ω^{2} x_{1}^{2} - 2 a_{+} x_{1} = 0 \\ x_{2} = - x_{1} - \frac{2 a_{+}}{ω^{2}} \end{array}$

y así, sucesivamente

Actividades

Se introduce

El coeficiente de rozamiento μ_s=μ_k, entre el bloque y el plano sobre el cual desliza, en el control titulado μ.
El ángulo del plano inclinado en grados, en el control titulado Angulo.
La masa m del bloque se ha fijado en m=1.0 kg.
La posición inicial x₀ del bloque en m, en el control titulado Posición.
La constante k del muelle elástico en N/m, en el control titulado k.

Se pulsa el botón titulado Nuevo

Se observa el movimiento del bloque deslizando sobre el plano inclinado.

En la parte inferior, se proporciona los datos relativos, al tiempo t en segundos, la posición x en cm y la velocidad v del bloque en m/s, y la energía del sistema formado por el bloque y el muelle, en cada instante.

Se dibujan mediante fechas las fuerzas sobre el bloque:

Componente del peso a lo largo del plano inclinado
Fuerza de rozamiento
Fuerza que ejerce el muelle deformado

En la parte superior derecha, muestra en un diagrama de barras la energía del sistema en cada instante.

El rectángulo de color negro, es la energía inicial
En color rojo, la energía potencial elástica del muelle deformado, que es siempre positiva
En color azul, la energía cinética del bloque
El color rosa, la energía potencial, que puede ser positiva o negativa, dependiendo de que el cuerpo esté por encima o por debajo del origen.

La energía va disminuyendo debido al trabajo de la fuerza de rozamiento

k (N/m): μ:
Posición (cm):
Angulo:

Referencias

Barrat C., Strobel G. L. Sliding friction and the harmonic oscillator. Am. J. Phys. 49 (5) May 1981, pp. 500-501

Experiencia de laboratorio

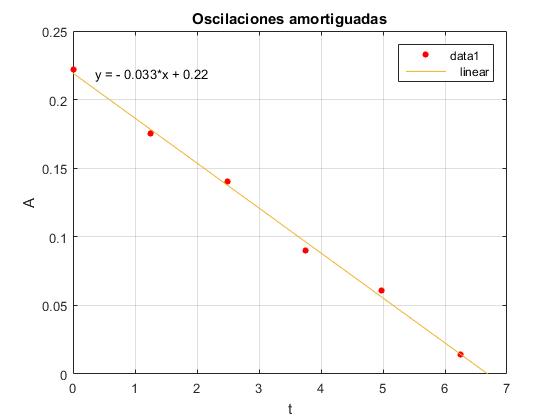
En una experiencia de laboratorio se han medido los desplazamientos máximos del bloque en función del tiempo

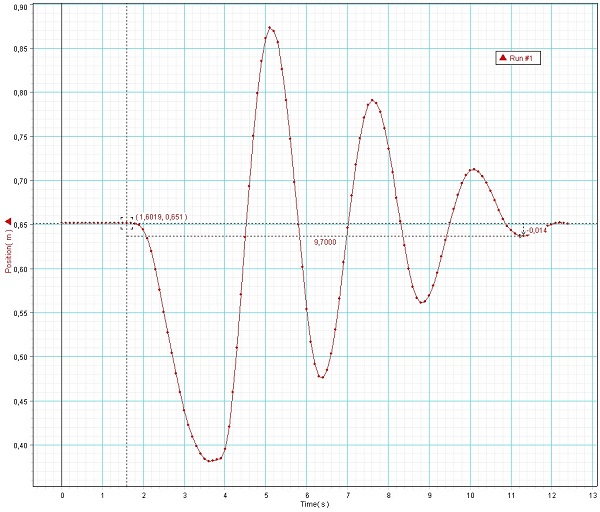
t (s)	A
0	0.222
1.25	0.175
2.49	0.140
3.75	0.09
4.98	0.061
6.25	0.014

Representamos los datos y hacemos un ajuste lineal.

%tiempo
x=[0,1.25,2.49,3.75,4.98,6.25];
%amplitud
y=[0.222,0.175,0.140,0.09,0.061,0.014];
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('t')
ylabel('A')
title('Oscilaciones amortiguadas')

En la ventana gráfica de MATLAB elegimos Tools/Basic fitting, activamos la casilla linear y obtenemos para la pendiente de la recta que mejor ajusta a los datos experimentales p1=-0.032773.