Un péndulo consiste en una varilla de masa M y longitud l sujeta por su extremo y un insecto de masa m que se mueve a velocidad constante v a lo largo de la varilla partiendo del centro de suspensión en el instante t=0.

En el instante inicial la varilla se desplaza un ángulo θ₀ y se suelta. Estudiaremos el movimiento posterior de este sistema oscilante

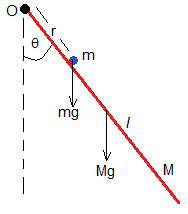
El momento de inercia de la varilla de masa M y longitud L, respecto de un eje perpendicular a la varilla y que pasa por su extremo O que es el punto de suspensión

${\displaystyle I_v=\frac{1}{12}M{l}^2+M{\left(\frac{l}{2}\right)}^2=\frac{1}{3}M{l}^2}$

El momento de inercia total de la varilla más el insecto (considerado una partícula) de masa m que se ha desplazado r a lo largo de la varilla es,

${\displaystyle I_O=\frac{1}{3}M{l}^2+m{r}^2}$

El momento de las fuerzas exteriores respecto de O son: (mr+ML/2)gsinθ. El centro de masa de la varilla se encuentra a l/2 del centro de suspensión O

La ecuación de la dinámica de rotación es

${\displaystyle \begin{array}{l}\frac{d\left(I_O\omega \right)}{dt}=-\left(mr+M\frac{l}{2}\right)g\sin \theta \\ \left(\frac{1}{3}M{l}^2+m{r}^2\right)\frac{d^2\theta }{d{t}^2}+2mr\frac{dr}{dt}\frac{d\theta }{dt}+\left(mr+M\frac{l}{2}\right)g\sin \theta =0\end{array}}$

Primera etapa

Utilizando las ecuaciones de Lagrange

La velocidad del insecto en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

La energía cinética del sistema formado por el péndulo y el insecto es

${\displaystyle E_k=\frac{1}{2}\left(\frac{1}{3}M{l}^2\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}m\left(v^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)=\frac{1}{2}\left\{\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2\right\}+\frac{1}{2}m{v}^2}$

Tomando el nivel cero de energía potencial el centro de suspensión, la energía potencial del sistema formado por el péndulo y el insecto es, E_p=-mgrcosθ-Mglcosθ/2

La Lagrangiana es

${\displaystyle L=\frac{1}{2}\left\{\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2\right\}+\frac{1}{2}m{v}^2-\left(mr+M\frac{l}{2}\right)g\cos \theta }$

La ecuación del movimiento del péndulo es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(\left(\frac{1}{3}M{l}^2+m{r}^2\right)\left(\frac{d\theta }{dt}\right)\right)+\left(mr+M\frac{l}{2}\right)g\sin \theta =0\\ \left(\frac{1}{3}M{l}^2+m{r}^2\right)\frac{d^2\theta }{d{t}^2}+2mr\frac{dr}{dt}\frac{d\theta }{dt}+\left(mr+M\frac{l}{2}\right)g\sin \theta =0\\ \frac{d^2\theta }{d{t}^2}+\frac{2mrv}{\frac{1}{3}M{l}^2+m{r}^2}\frac{d\theta }{dt}+\frac{\left(mr+M\frac{l}{2}\right)g}{\frac{1}{3}M{l}^2+m{r}^2}\sin \theta =0\end{array}}$

El insecto se mueve con velocidad constante r=vt, dr/dt=v. La ecuación diferencial del movimiento es

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{2m{v}^{2}t}{\frac{1}{3}M{l}^2+m{v}^2{t}^2}\frac{d\theta }{dt}+\frac{\left(mvt+M\frac{l}{2}\right)g}{\frac{1}{3}M{l}^2+m{v}^2{t}^2}\sin \theta =0}$

Esta ecuación diferencial nos recuerda a la de las oscilaciones amortiguadas. Para oscilaciones de pequeña amplitud sinθ≈θ

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =0}$

con los parámetros: amortiguamiento, γ y frecuencia propia, ω₀ dependientes del tiempo t

Representamos los parámetros amortiguamiento γ y frecuencia propia, ω₀ desde el instante t=0, el insecto se encuentra en el punto de suspensión O, hasta que llega al final de la varilla t=l/v con los siguientes datos: una varilla de longitud l=1 m, de masa M=1 kg y un insecto de masa m=0.2 kg que se mueve a lo largo de la varilla con velocidad constante v=0.1 m/s

M=1; %masa varilla
L=1; %longitud varilla
m=0.2; %masa insecto
v=0.1; %velocidad coonstante del insecto

subplot(2,1,1)
gamma=@(t) m*v^2*t./(M*L^2/3+m*(v*t).^2);
fplot(gamma,[0,L/v])
xlabel('t')
ylabel('\gamma')
title('Amortiguamiento')

subplot(2,1,2)
w0=@(t) sqrt((m*v*t+M*L/2)*9.8./(M*L^2/3+m*(v*t).^2));
fplot(w0,[0,L/v])
xlabel('t')
ylabel('\omega_0')
title('Frecuencia propia')

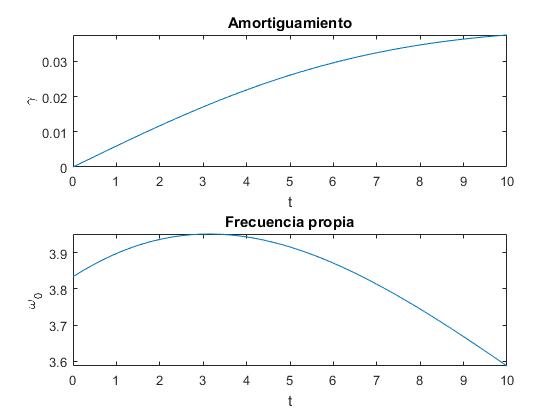
Cuando el insecto se encuentra en el punto de suspensión t=0, y cuando se encuentra en el extremo de la varilla t=l/v, las frecuencias angulares de oscilación del sistema valen, respectivamente

${\displaystyle \begin{array}{l}{\omega }_0^2=\frac{3}{2}\frac{g}{L}\\ {\omega }_0^2=\frac{3}{2}\left(\frac{M+2m}{M+3m}\right)\frac{g}{L}\end{array}}$

Entre ambos valores extemos, la frecuencia angular ω₀ alcanza un valor máximo, tal como apreciamos en la figura inferior

Segunda etapa

Cuando el insecto alcanza el extremo inferior del péndulo en el instante t=l/v, se mantiene en dicha posición en reposo. La ecuación diferencial del movimiento para t>l/v con r=l y v=0, es

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{\left(m+\frac{M}{2}\right)g}{\left(m+\frac{M}{3}\right)l}\sin \theta =0}$

Movimiento completo

Resolvemos las ecuaciones diferenciales que describen las dos etapas del movimiento del insecto, por procedimientos numéricos con las condiciones iniciales:

1. Primera etapa: en el instante t=0, θ=θ₀, y dθ/dt=0, parte del reposo

2. Segunda etapa: las condiciones iniciales igual a las finales de la etapa anterior, en el instante t=l/v, θ=θ₁, y dθ/dt=(dθ/dt)₁

Consideremos el siguiente oscilador:

• La velocidad del insecto, v=0.1 m/s
• La masa del insecto, m=0.25 kg
• El desplazamiento angular inicial del péndulo, θ₀=π/6 (30°)
• La masa de la varilla, M=1 kg
• La longitud de la varilla, l=1 m

v=0.1; %velocidad del insecto
m=0.25; %masa del insecto
M=1; %masa de la varilla
L=1; %longitud de la varilla
aIni=pi/6; %ángulo inicial
hold on
%primera etapa
fg=@(t,x)[x(2);-2*m*v^2*t*x(2)/(M*L*L/3+m*(v*t)^2)-
(m*v*t+M*L/2)*9.8*sin(x(1))/(M*L*L/3+m*(v*t)^2)];
[t,x]=ode45(fg,[0,L/v],[aIni,0]);
plot(t,x(:,1))
%segunda etapa
fg=@(t,x) [x(2);-(m+M/2)*sin(x(1))/(M*L/3+m*L)];
[t,x]=ode45(fg,[L/v,2.5*L/v],[x(end,1),x(end,2)]);
plot(t,x(:,1))
hold off
grid on
xlabel('t')
ylabel('x');
title('Péndulo')

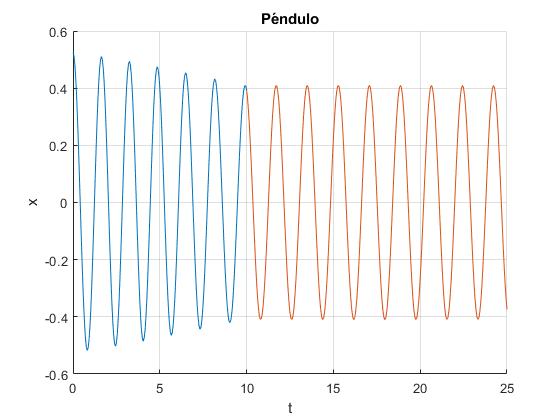
• En color azul, la amplitud variable del oscilador mientras el insecto se desplaza a lo largo de la varilla
• En color rosa, la amplitud constante del oscilador, cuado el insecto permanece en el extremo inferior de la varilla

Con el cursor medimos aproximadamente, el desplazamiento máximo del péndulo, 0.4094*180/pi= 23.4569 grados

Energía

Dado que el insecto se mueve con velocidad constante v, su energía cinética inicial mv²/2 coincide con la final.

• En el instante t=0, el insecto se encuentra en el punto de suspensión, la energía inicial del sistema es la energía potencial de la varilla desviada un ángulo θ₀

${\displaystyle E_0=-Mg\left(\frac{l}{2}\right)\cos {\theta }_0+\frac{1}{2}m{v}^2}$

• En el instante t, con r=v·t

${\displaystyle E=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}m{v}^2-\left(M\frac{l}{2}+mr\right)g\cos \theta }$

• En el instante t=l/v, el insecto ha llegado al final de la varilla, r=l. La energía final será

${\displaystyle E_f=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{l}^2\right){\left(\frac{d\theta }{dt}\right)}_f^2+\frac{1}{2}m{v}^2-\left(ml+M\frac{l}{2}\right)g\cos {\theta }_f}$

donde θ_f es el ángulo de desviación y (dθ/dt)_f es la velocidad angular final del péndulo en el instante t=l/v.

• Cuando el insecto permanece en el extremo inferior de la varilla, t>l/v

La energía cinética mv²/2 se disipa en el choque inelástico entre el insecto y el extremo de la varilla. A partir del instante t=l/v, tenemos un péndulo compuesto cuya energía es constante y cuya amplitud θ₁ es

${\displaystyle E_f=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{l}^2\right){\left(\frac{d\theta }{dt}\right)}_f^2-\left(M\frac{l}{2}+ml\right)g\cos {\theta }_f=-\left(M\frac{l}{2}+ml\right)g\cos {\theta }_1}$

v=0.1; %velocidad del insecto
m=0.25; %masa del insecto
M=1; %masa de la varilla
L=1; %longitud de la varilla
aIni=pi/6; %ángulo inicial
hold on
E0=-M*L*9.8*cos(aIni)/2; %energía inicial
%primera etapa
fg=@(t,x)[x(2);-2*m*v^2*t*x(2)/(M*L*L/3+m*(v*t)^2)-
(m*v*t+M*L/2)*9.8*sin(x(1))/(M*L*L/3+m*(v*t)^2)];
[t,x]=ode45(fg,[0,L/v],[aIni,0]);
E=-9.8*(M*L/2+m*v*t).*cos(x(:,1))+(M*L*L/3+m*(v*t).^2).*x(:,2).^2/2;
plot(t,E)
line([L/v,3*L/(2*v)],[E(end),E(end)]) %energía final constante

hold off
grid on
xlabel('t')
ylabel('E');
title('Energías')

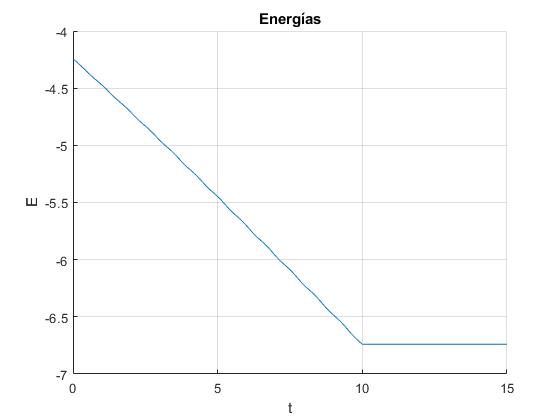
La energía disminuye, hasta que se hace constante cuando el insecto permanece en el extremo inferior de la varilla

La amplitud de la oscilación del péndulo es θ₁=23.51°

>> th_1=acosd(-E(end)/((M*L/2+m*L)*9.8))
th_1 =   23.5112

Fuerza sobre el insecto

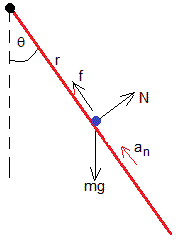
Las fuerzas que actúan sobre el insecto, s son:

• El peso, mg
• La reacción de la varilla, N
• La fuerza f que ejerce la varilla sobre el insecto para que se desplace a velocidad constante

${\displaystyle f=mg\cos \theta +mr{\left(\frac{d\theta }{dt}\right)}^2}$

Utilizamos la dinámica del movimiento circular para obtener la misma expresión: masa por aceleración normal a_n, es igual a la suma de las fuerzas en la dirección radial

${\displaystyle mr{\left(\frac{d\theta }{dt}\right)}^2=f-mg\cos \theta }$

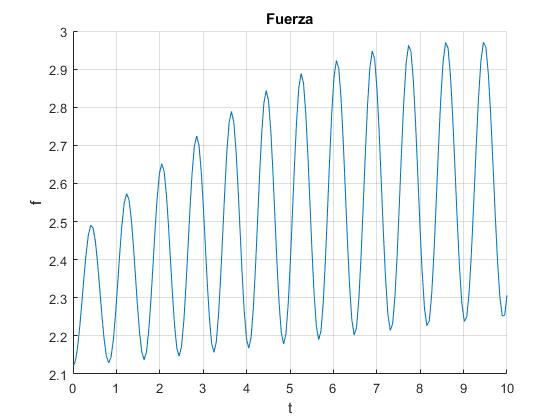
Representamos la fuerza f en función del tiempo t,

v=0.1; %velocidad del insecto
m=0.25; %masa del insecto
M=1; %masa de la varilla
L=1; %longitud de la varilla
aIni=pi/6; %ángulo inicial
hold on
%primera etapa
fg=@(t,x)[x(2);-2*m*v^2*t*x(2)/(M*L*L/3+m*(v*t)^2)-
(m*v*t+M*L/2)*9.8*sin(x(1))/(M*L*L/3+m*(v*t)^2)];
[t,x]=ode45(fg,[0,L/v],[aIni,0]);
f=m*9.8*cos(x(:,1))+m*v*t.*x(:,2).^2;
plot(t,f)
grid on
xlabel('t')
ylabel('f');
title('Fuerza')

Calculamos el trabajo de la fuerza interna f entre el insecto y la varilla, para que se mueva con velocidad constante

${\displaystyle W={\displaystyle \underset{0}{\overset{l}{\int }}-f·dr}={\displaystyle \underset{0}{\overset{l/v}{\int }}-(fv)·dt}=E_f-E_0}$

Combinamos los dos script anteriores, energía y fuerza para calcular el trabajo W de la fuerza f y verificar que es igual a la diferencia entre las energías final e inicial.

...
E0=-M*L*9.8*cos(aIni)/2; %energía inicial
....
E=-9.8*(M*L/2+m*v*t).*cos(x(:,1))+(M*L*L/3+m*(v*t).^2).*x(:,2).^2/2;
f=m*9.8*cos(x(:,1))+m*v*t.*x(:,2).^2; %fuerza
...

>> W=trapz(t,-f*v) %trabajo de f
W =   -2.4937
>> E(end)-E0
ans =   -2.4963

Actividades

Se introduce

• La masa m del insecto en el control titulado Masa insecto
• La velocidad constante v del insecto sobre la varilla en el control titulado Velocidad
• La masa de la varilla M se ha fijado en 1 kg
• La longitud de la varilla l se ha fijado en 1 m
• La desviación θ₀ del péndulo en el instante t=0 en el control titulado Desviación

Se pulsa el botón titulado Nuevo

Observamos el movimiento del péndulo, como va disminuyendo su amplitud, hasta que el insecto alcanza el extremo inferior de la varilla, a partir de ese momento la amplitud de la oscilación es constante

Observamos en la parte inferior, la representación gráfica de la posición angular del péndulo en función del tiempo. Las divisiones en el eje X marcan el periodo P₀=2π/ω₀, que corresponde al periodo inicial, cuando el insecto se encuentra en el punto de suspensión O. De este modo, podemos observar como va cambiando la amplitud y el periodo de la oscilación a medida que el insecto se desplaza a lo largo de la varilla

En la esquina superior izquierda, se proporcionan los datos, del tiempo t, posición angular θ y velocidad angular dθ/dt

Esperamos hasta que el insecto llegue al extremo inferior de la varilla, utilizamos los botones || y '>| hasta que el oscilador alcance el máximo desplazamiento (velocidad angular nula) a uno u otro lado de la vertical. La amplitud constante final es, θ=23.56°

Valores medios. Aproximaciones

En este apartado, vamos a establecer una relación entre la amplitud inicial θ₀ de la oscilación del péndulo y la amplitud final θ₁ cuando el insecto permanece en reposo en el extremo inferior de la varilla.

Hemos comprobado que el trabajo de la fuerza f que ejerce la varilla sobre el insecto es igual a la variación de energía del sistema oscilante formado por la varilla y el insecto.

${\displaystyle \begin{array}{l}W={\displaystyle \underset{0}{\overset{r}{\int }}-f·dr}=E-E_0\\ -{\displaystyle \underset{0}{\overset{r}{\int }}\left(mg\cos \theta +mr{\left(\frac{d\theta }{dt}\right)}^2\right)dr}=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2-\left(M\frac{l}{2}+mr\right)g\cos \theta -M\frac{l}{2}g\cos {\theta }_0\end{array}}$

Utilizando la relación trigonométrica, 1-cosθ=2sin²(θ/2)

${\displaystyle \begin{array}{l}-{\displaystyle \underset{0}{\overset{r}{\int }}\left(mg\left(1-2{\sin }^2\left(\frac{\theta }{2}\right)\right)+mr{\left(\frac{d\theta }{dt}\right)}^2\right)dr}=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2-\left(M\frac{l}{2}+mr\right)g\left(1-2{\sin }^2\left(\frac{\theta }{2}\right)\right)+M\frac{l}{2}g\cos {\theta }_0\\ -mgr+{\displaystyle \underset{0}{\overset{r}{\int }}\left(2mg{\sin }^2\left(\frac{\theta }{2}\right)-mr{\left(\frac{d\theta }{dt}\right)}^2\right)dr=}\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2-mgr+2\left(M\frac{l}{2}+mr\right)g{\sin }^2\left(\frac{\theta }{2}\right)-Mlg{\sin }^2\left(\frac{{\theta }_0}{2}\right)\end{array}}$

Cuando la amplitud es pequeña, sin²(θ/2)≈θ²/4

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{r}{\int }}\left(mg\frac{{\theta }^2}{2}-mr{\left(\frac{d\theta }{dt}\right)}^2\right)dr\approx }\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}\left(M\frac{l}{2}+mr\right)g{\theta }^2-\frac{1}{2}Mg\frac{l}{2}{\theta }_0^2\\ {\displaystyle \underset{0}{\overset{r}{\int }}\left(mg\frac{{\theta }^2}{2}-mr{\left(\frac{d\theta }{dt}\right)}^2\right)dr\approx }E-E_0\end{array}}$

En el segundo miembro, tenemos la energía E de un movimiento armónico simple. Cuando el insecto se mueve muy despacio, el péndulo oscila varias veces, sin que cambie apreciablemente de posición. Sustituimos la energía cinética y potencial por sus valores medios

• Valor medio de la energía cinética

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2\\ \langle E_k\rangle =\frac{1}{2}\left(\frac{1}{3}M{l}^2+m{r}^2\right)\langle {\left(\frac{d\theta }{dt}\right)}^2\rangle =\frac{E}{2}\\ \langle {\left(\frac{d\theta }{dt}\right)}^2\rangle =\frac{E}{\frac{1}{3}M{l}^2+m{r}^2}\end{array}}$

• Valor medio de la energía potencial

${\displaystyle \begin{array}{l}\langle E_p\rangle \approx \frac{1}{2}\left(M\frac{l}{2}+mr\right)g\langle {\theta }^2\rangle =\frac{E}{2}\\ \langle {\theta }^2\rangle =\frac{E}{\left(M\frac{l}{2}+mr\right)g}\end{array}}$

• Valor medio del integrando

${\displaystyle mg\frac{\langle {\theta }^2\rangle }{2}-mr\langle {\left(\frac{d\theta }{dt}\right)}^2\rangle =mg\frac{E}{2\left(Mg\frac{l}{2}+mgr\right)}-mr\frac{E}{\frac{1}{3}M{l}^2+m{r}^2}}$

En forma diferencial, el trabajo es igual a la variación de energía E del oscilador, se escribe

${\displaystyle \begin{array}{l}\left(mg\frac{E}{2\left(Mg\frac{l}{2}+mgr\right)}-mr\frac{E}{\frac{1}{3}M{l}^2+m{r}^2}\right)dr=dE\\ \frac{dE}{E}=\left(\frac{1}{2\left(\frac{M}{m}\frac{l}{2}+r\right)}-\frac{r}{\frac{1}{3}\frac{M}{m}{l}^2+r^2}\right)dr\end{array}}$

Integramos desde la posición inicial del insecto r=0 a la posición r

${\displaystyle \begin{array}{l}{\displaystyle \underset{E_0}{\overset{E}{\int }}\frac{dE}{E}={\displaystyle \underset{0}{\overset{r}{\int }}\left(\frac{1}{2\left(\frac{M}{m}\frac{l}{2}+r\right)}-\frac{r}{\frac{1}{3}\frac{M}{m}{l}^2+r^2}\right)dr}}\\ \ln (E)-\ln (E_0)=\frac{1}{2}\ln \left(\frac{M}{m}\frac{l}{2}+r\right)-\frac{1}{2}\ln \left(\frac{M}{m}\frac{l}{2}\right)-\frac{1}{2}\ln \left(\frac{1}{3}\frac{M}{m}{l}^2+r^2\right)+\frac{1}{2}\ln \left(\frac{1}{3}\frac{M}{m}{l}^2\right)\\ \ln \frac{E}{E_0}=\frac{1}{2}\ln \frac{\left(Ml+2mr\right)l}{M{l}^2+3m{r}^2}\\ E=E_0\sqrt{\frac{\left(ml+2mr\right)l}{M{l}^2+3m{r}^2}}\end{array}}$

Cuando el insecto llega al extremo inferior de la varilla, r=l

${\displaystyle E_f=E_0\sqrt{\frac{\left(Ml+2ml\right)l}{M{l}^2+3m{l}^2}}=E_0\sqrt{\frac{M+2m}{M+3m}}}$

Relacionamos las amplitudes, inicial θ₀ y la final θ₁

El insecto está en el centro de suspensión, r=0. El péndulo se desplaza un ángulo θ₀ y se suelta, su energía es E₀ es

${\displaystyle E_0=\frac{1}{2}Mg\frac{l}{2}{\theta }_0^2}$

El insecto permanece en el extremo inferior de la varilla, r=l. La energía el péndulo alcanza el máximo desplazamiento angular θ₁, la velocidad angular dθ/dt=0, es nula

${\displaystyle E_f=\frac{1}{2}\left(M\frac{l}{2}+ml\right)g{\theta }_1^2}$

La relación entre amplitudes es

${\displaystyle \begin{array}{l}\frac{1}{2}\left(M\frac{l}{2}+ml\right)g{\theta }_1^2=\frac{1}{2}Mg\frac{l}{2}{\theta }_0^2\sqrt{\frac{M+2m}{M+3m}}\\ {\theta }_1^2={\theta }_0^2\sqrt{\frac{M^2}{\left(M+3m\right)\left(M+2m\right)}}\end{array}}$

Ejemplo

Sea la masa de la varilla, M=1, y la masa del insecto m=0.25

La varilla con el insecto en el centro de suspensión se desplaza un ángulo θ₀=30° y se suelta. Cuando el insecto llega al otro extremo de la varilla, la amplitud de la oscilación es θ₁=23.57°, que hemos medido en el programa interactivo

>> M=1;
>> m=0.25;
>> th_1=30*(M^2/((M+3*m)*(M+2*m)))^(1/4)
th_1 =   23.5689

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1177, pp. 288-291