Una máquina de Atwood de masa variable que oscila

Estado inicial

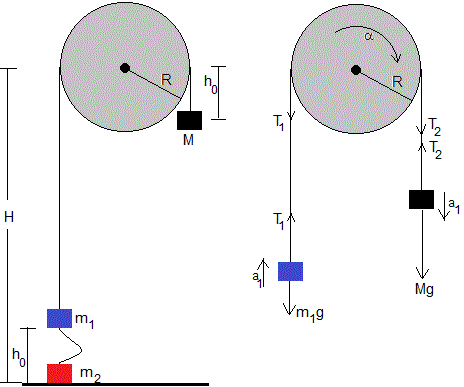
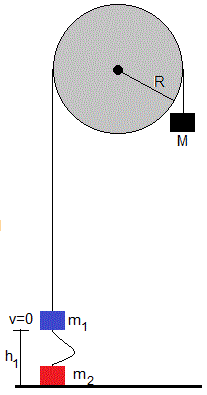
La situación inicial, se muestra a la izquierda en la figura. El cuerpo de masa m₂ está en el suelo y el cuerpo de masa m₁ desplazado una altura h₀<d. La cuerda que une que une los dos cuerpos de longitud d no tiene efecto alguno sobre su movimiento. El cuerpo de masa m₂ continúa en reposo en el suelo. La energía inicial es potencial, referida al suelo es

E₀=Mg(H-h₀)+m₁gh₀.

Donde H es la altura del eje de la polea

Movimiento del cuerpo de masa m₁

En la parte derecha de la figura, se ha dibujado las fuerzas sobre cada uno de los tres cuerpos que intervienen. Las ecuaciones del movimientos son

${\begin{cases} M g - T_{2} = M a_{1} \\ T_{1} - m_{1} g = m_{1} a_{1} \\ T_{2} R - T_{1} R = I α \end{cases} {\begin{cases} M g - T_{2} = M a_{1} \\ T_{1} - m_{1} g = m_{1} a_{1} \\ T_{2} - T_{1} = \frac{I}{R^{2}} a_{1} \end{cases}$

Donde I es el momento de inercia de la polea y α=a₁/R la aceleración angular de la polea

Sumamos las tres ecuaciones y despejamos la aceleración a₁

$a_{1} = \frac{M - m_{1}}{M + m_{1} + \frac{I}{R^{2}}} g$

La posición y velocidad del cuerpo de masa m₁

$\begin{array}{l} y = h_{0} + \frac{1}{2} a_{1} t^{2} \\ v = a_{1} t \end{array}$

Conservación del momento angular

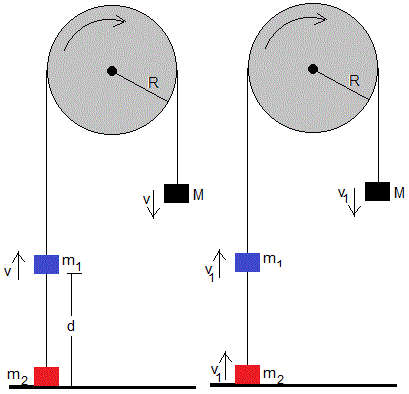
Cuando el cuerpo de masa m₁ se ha desplazado hasta la altura d, su velocidad es

$\begin{array}{l} d = h_{0} + \frac{1}{2} a_{1} t^{2} \\ v = a_{1} t = \sqrt{2 a_{1} (d - h_{0})} \end{array}$

El tiempo que tarda el cuerpo de masa m₁ en llegar a esta posición es

$t_{1} = \sqrt{\frac{2 (d - h_{0})}{a_{1}}}$

La energía del sistema no ha cambiado

$\begin{array}{l} E_{0} = \frac{1}{2} m_{1} v^{2} + \frac{1}{2} M v^{2} + \frac{1}{2} I ω^{2} + m_{1} g d + M g (H - d) = \\ \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) v^{2} + m_{1} g d + M g (H - d) \end{array}$

La cuerda que une este cuerpo y el de masa m₂ está tensa. Al cabo de un intervalo de tiempo que supondremos muy breve, los cuerpos alcanzan una velocidad común v₁ que se obtiene aplicando el principio de conservación del momento angular

El momento angular inicial es

$L_{i} = (m_{1} + M) v R + I ω = (m_{1} + M + \frac{I}{R^{2}}) v R$

El momento angular final es

$L_{f} = (m_{1} + M + m_{2}) v_{1} R + I ω_{1} = (m_{1} + M + m_{2} + \frac{I}{R^{2}}) v_{1} R$

Despejamos la velocidad final v₁

$v_{1} = \frac{m_{1} + M + \frac{I}{R^{2}}}{m_{1} + M + m_{2} + \frac{I}{R^{2}}} v = γ v$

La energía del sistema cambia

$\begin{array}{l} E_{1} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{1}^{2} + \frac{1}{2} M v_{1}^{2} + \frac{1}{2} I ω_{1}^{2} + m_{1} g d + M g (H - d) = \\ \frac{1}{2} (m_{1} + m_{2} + M + \frac{I}{R^{2}}) v_{1}^{2} + m_{1} g d + M g (H - d) \end{array}$

La variación de energía es

$\begin{array}{l} Δ E_{1} = E_{1} - E_{0} = \frac{1}{2} (m_{1} + m_{2} + M + \frac{I}{R^{2}}) v_{1}^{2} - \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) v^{2} = \\ \frac{1}{2} m_{2} v_{1}^{2} + \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) (v_{1}^{2} - v^{2}) \end{array}$

Movimiento de los dos cuerpos

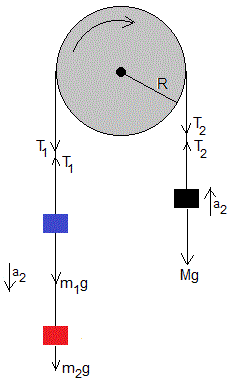
Los cuerpos de masas m₁ y m₂ se mueven hacia arriba, disminuyendo su velocidad ya que m₁+m₂>M, la aceleración es

Las ecuaciones del movimiento son:

$\begin{array}{l} {\begin{cases} (m_{1} + m_{2}) g - T_{1} = (m_{1} + m_{2}) a_{2} \\ T_{2} - M g = M a_{2} \\ T_{1} R - T_{2} R = I α \end{cases} \\ {\begin{cases} (m_{1} + m_{2}) g - T_{1} = (m_{1} + m_{2}) a_{2} \\ T_{2} - M g = M a_{2} \\ T_{1} - T_{2} = \frac{I}{R^{2}} a_{2} \end{cases} \end{array}$

Sumamos las tres ecuaciones y despejamos la aceleración a₂

$a_{2} = \frac{m_{1} + m_{2} - M}{M + m_{1} + m_{2} + \frac{I}{R^{2}}} g$

La aceleración a₂ es de sentido contrario a la velocidad inicial v₁, por lo que el cuerpo m₁ alcanzará un desplazamiento máximo hasta que la velocidad se haga cero. Después se moverá hacia abajo hasta que el cuerpo de masa m₂ choque con el suelo, la velocidad de los cuerpos será v₁ pero de sentido contrario.

La posición y velocidad del cuerpo de masa m₁

$\begin{array}{l} y = d + v_{1} t - \frac{1}{2} a_{2} t^{2} \\ v = v_{1} - a_{2} t \end{array}$

El tiempo que invierte en esta etapa es el que tarda en subir desde y=d y regresar a la misma posición

$t_{2} = 2 \frac{v_{1}}{a_{2}}$

Choque del cuerpo de masa m₂ con el suelo

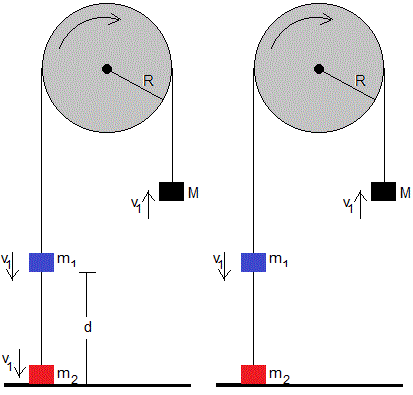
El cuerpo de masa m₂ lleva una velocidad v₁ choca inelásticamente con el suelo, reduciendo su velocidad a cero en un intervalo de tiempo muy corto. La energía del sistema antes del choque es E₁ y después del choque

$\begin{array}{l} E_{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} M v_{1}^{2} + \frac{1}{2} I ω_{1}^{2} + m_{1} g d + M g (H - d) = \\ \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) v_{1}^{2} + m_{1} g d + M g (H - d) \end{array}$

El sistema pierde una energía

$Δ E_{2} = - \frac{1}{2} m_{2} v_{1}^{2}$

Final del primer periodo

El cuerpo de masa m₂ no tiene efecto sobre el movimiento posterior de los otros cuerpos. El cuerpo de masa m₁ se mueva hacia abajo con aceleración a₁ de sentido contrario a la velocidad inicial v₁, ya que m₁<M

La posición y velocidad de dicho cuerpo

${\begin{cases} v = - v_{1} + a_{1} t \\ y = d - v_{1} t + \frac{1}{2} a_{1} t^{2} \end{cases}$

La velocidad del cuerpo de masa m₁ se anula en la posición h₁

$\begin{array}{l} {\begin{cases} 0 = - v_{1} + a_{1} t \\ h_{1} = d - v_{1} t + \frac{1}{2} a_{1} t^{2} \end{cases} \\ h_{1} = d - \frac{1}{2} \frac{v_{1}^{2}}{a_{1}} = d - \frac{1}{2} \frac{γ^{2} 2 a_{1} (d - h_{0})}{a_{1}} = \\ d - γ^{2} (d - h_{0}) = γ^{2} h_{0} + (1 - γ^{2}) d \end{array}$

El tiempo que invierte en esta etapa es

$t_{3} = \frac{v_{1}}{a_{1}}$

Movimiento completo

Alturas iniciales.

En general, tendremos que

$h_{n} = γ^{2} h_{n - 1} + (1 - γ^{2}) d$

La relación de recurrencia se convierte en

$h_{n} = γ^{2 n} h_{0} + (1 - γ^{2 n}) d$

Periodo

El periodo de la primera oscilación es la suma de los tiempos de las tres etapas

$\begin{array}{l} P_{1} = t_{1} + t_{2} + t_{3} = \sqrt{\frac{2 (d - h_{0})}{a_{1}}} + v_{1} (\frac{2}{a_{2}} + \frac{1}{a_{1}}) = \sqrt{\frac{2 (d - h_{0})}{a_{1}}} + γ \sqrt{2 a_{1} (d - h_{0})} (\frac{2}{a_{2}} + \frac{1}{a_{1}}) = \\ \sqrt{2 (d - h_{0})} (\frac{1}{\sqrt{a_{1}}} + γ \sqrt{a_{1}} (\frac{2}{a_{2}} + \frac{1}{a_{1}})) \end{array}$

Análogamente, obtendremos el periodo de la segunda, tercera, ... oscilación

Energía disipada

Se disipa energía en dos momentos:

Cuando se pone en movimiento el cuerpo de masa m₂ unido mediante una cuerda inextensibre de longitud d al cupero de masa m₁
Cuando el cuerpo de masa m₂ choca inelásticamente con el suelo

La variación de energía durante el primer periodo

$\begin{array}{l} Δ E = Δ E_{1} + Δ E_{2} = \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) (v_{1}^{2} - v^{2}) = \frac{1}{2} (m_{1} + M + \frac{I}{R^{2}}) (γ^{2} - 1) v^{2} \\ = (γ^{2} - 1) (M - m_{1}) g (d - h_{0}) \end{array}$

Análogamente, obtendremos la variación de energía de la segunda, tercera, ... oscilación

Ejemplo

Sea el sistema formado por

Cuerpo de masa M=33.95 g
Cuerpo de masa m₁=28.95 g
Cuerpo de masa m₂=8.70 g
Polea de momento de inercia I/R²=3 g
Distancia entre los cuerpos, d=54.5 cm
Altura inicial, h₀=14 cm

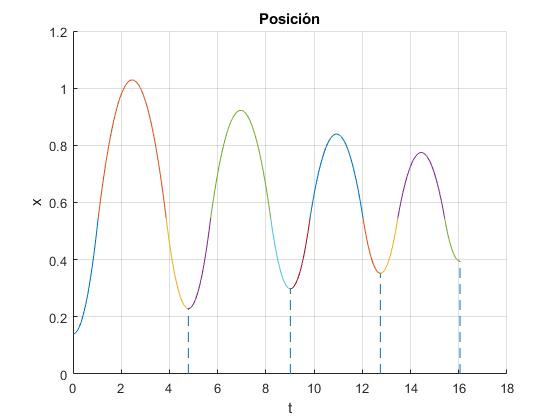
Representamos la posición y del cuerpo de masa m₁ en función del tiempo t durante cuatro oscilaciones

M=33.95/1000; %contapeso
m1=28.95/1000;
m2=8.70/1000;
I=3/1000; %momento de inercia I/R^2
a1=(M-m1)*9.8/(M+m1+I);
a2=-(m1+m2-M)*9.8/(M+m1+m2+I);
gamma=(M+m1+I)/(M+m1+m2+I);
d=0.545; %distancia entre m1 y m2
h0=0.14; %altura inicial de m1
hold on
P=0;
for i=1:4
    t1=sqrt(2*(d-h0)/a1)+P;
    fplot(@(t) h0+a1*(t-P).^2/2,[P,t1])
    v1=gamma*a1*(t1-P);
    t2=-2*v1/a2+t1; %sube y baja de x=d
    fplot(@(t) d+v1*(t-t1)+a2*(t-t1).^2/2,[t1,t2])
%sigue bajando sin m2 hasta que se detiene
    t3=v1/a1+t2;
    fplot(@(t) d-v1*(t-t2)+a1*(t-t2).^2/2,[t2,t3])
    P=t3;
    h0=d-gamma^2*(d-h0);
    line([t3,t3],[0,h0],'lineStyle','--')
end
hold off
grid on
xlabel('t')
ylabel('x')
title('Posición')

Las líneas a trazos, señalan los periodos, que cuya duración va disminuyendo.

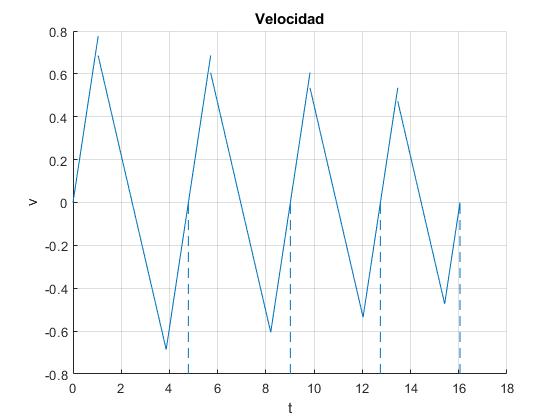
Representamos la velocidad v de los cuerpos en función del tiempo t durante cuatro oscilaciones

M=33.95/1000; %contapeso
m1=28.95/1000;
m2=8.70/1000;
I=3/1000; %momento de inercia I/R^2
a1=(M-m1)*9.8/(M+m1+I);
a2=-(m1+m2-M)*9.8/(M+m1+m2+I);
gamma=(M+m1+I)/(M+m1+m2+I);
d=0.545; %distancia entre m1 y m2
h0=0.14; %altura inicial de m1
hold on
P=0;
for i=1:4
    t1=sqrt(2*(d-h0)/a1)+P;
    line([P,t1],[0,a1*(t1-P)])
    v1=gamma*a1*(t1-P);
    t2=-2*v1/a2+t1; %sube y baja de x=d
    line([t1,t2],[v1,v1+a2*(t2-t1)])
    t3=v1/a1+t2;
    line([t2,t3],[-v1, -v1+a1*(t3-t2)])
    P=t3;
    line([t3,t3],[-0.8,0],'lineStyle','--')
    h0=d-gamma^2*(d-h0);
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

La velocidad no es una función continua, en el instante t₁, ya que pasa de v a v₁ cuando la altura del cuerpo es y=d

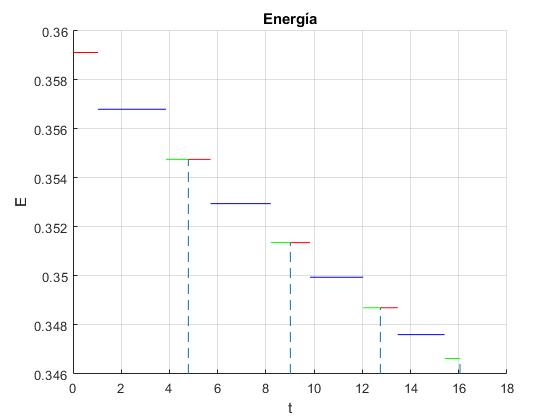
Representamos la energía E de los cuerpos en función del tiempo t durante cuatro oscilaciones

M=33.95/1000; %contapeso
m1=28.95/1000;
m2=8.70/1000;
I=3/1000; %momento de inercia I/R^2
a1=(M-m1)*9.8/(M+m1+I); %aceleraciones
a2=-(m1+m2-M)*9.8/(M+m1+m2+I);
gamma=(M+m1+I)/(M+m1+m2+I);
d=0.545; %distancia entre m1 y m2
h0=0.14; %altura inicial de m1
hold on
P=0;
E1=M*9.8*(1.1-h0)+m1*9.8*h0;
for i=1:4
    t1=sqrt(2*(d-h0)/a1)+P;
    line([P,t1],[E1,E1],'color','r')
    v1=gamma*a1*(t1-P);
    E2=M*9.8*(1.1-d)+m1*9.8*d+(M+m1+m2+I)*v1^2/2;
    t2=-2*v1/a2+t1; %sube y baja de x=d
    line([t1,t2],[E2,E2],'color','b')
    t3=v1/a1+t2;
    E3=M*9.8*(1.1-d)+m1*9.8*d+(M+m1+I)*v1^2/2;
    line([t2,t3],[E3,E3],'color','g')
    line([t3,t3],[0.346,E3],'lineStyle','--')
    P=t3;
    h0=d-gamma^2*(d-h0);
    E1=M*9.8*(1.1-h0)+m1*9.8*h0;
end
hold off
grid on
xlabel('t')
ylabel('E')
title('Energía')

Actividades

Mediante este programa interactivo, se observa la animación del sistema descrito en el ejemplo anterior. En la parte derecha, se representa la altura y del cuerpo de masa m₁ en función del tiempo t

En la parte superior derecha, se proporcionan los datos de

Tiempo, t en s
Altura y en cm
Velocidad v en cm/s
Aceleración a en m/s²

Referencias

B. Lucatto, M.B. Caprecci, J.V.A. Gonçalves, B.N. Sismanoglu. Máquina de Atwood com massa variável em movimento oscilatório atípico. Revista Brasileira de Ensino de Física, v. 36, n. 2, 2503 (2014)