Oscilador amortiguado de masa variable

En la página titulada Oscilador de masa variable, estudiamos un sistema de masa variable consistente en un depósito de agua con un orificio en su parte inferior que está colgado de un muelle de constante elástica k. El oscilador es libre, ya que se ha despreciado el rozamiento con el aire.

Aunque los dos osciladores son aparentemente similares, la solución del problema como veremos, es completamente diferente.

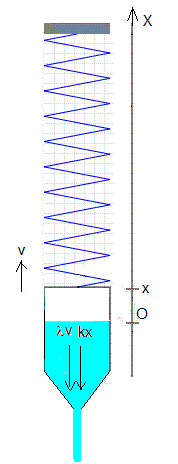
Un recipiente lleno de arena de masa m₀ cuelga de un muelle elástico de constante k. En el fondo del recipiente hay un orificio de modo que su masa decrece linealmente con el tiempo a razón de c kg/s que se mantiene constante independientemente de que esté estacionario o en movimiento oscilatorio. Supondremos que el oscilador está débilmente amortiguado por una fuerza de rozamiento proporcional a la velocidad λv.

Hemos formulado las ecuaciones de un sistema de masa variable en varias páginas, una de ellas, es el movimiento vertical de un cohete,

$m \frac{d v}{d t} + u \frac{d m}{d t} = F_{e x t}$

Donde m es la masa del recipiente que contiene la arena, u es la velocidad de escape de la arena relativa al recipiente y dm/dt la variación de su masa con el tiempo, F_ext es la resultante de las fuerzas que se aplican en el centro de masas:

El peso m(t)g
La fuerza que ejerce el muelle elástico porporcional al desplazamiento del muelle desde su posición inicial x=0, -k(x+x₀), donde x₀(t)=m(t)g/k es la posición de equilibrio del muelle
La fuerza de rozamiento, proporcional a la velocidad F_r=-λ(dx/dt)

Supondremos que la velocidad relativa de la arena que sale u≈0 respecto del recipiente es nula, y que la masa m del depósito decrece linealmente con el tiempo m=m₀-ct

Expresamos la ecuación del movimiento en forma de ecuación diferencial

$m \frac{d^{2} x}{d t^{2}} + λ \frac{d x}{d t} + k x = 0$

Se trata de la ecuación diferencial de las oscilaciones amortiguadas, salvo que la masa m no es constante. Resolveremos esta ecuación diferencial aplicando procedimientos numéricos y buscando una solución analítica aproximada

Solución numérica

Expresamos la ecuación diferencial de la forma

$\frac{d^{2} x}{d t^{2}} = - \frac{1}{m_{0} - c t} (λ \frac{d x}{d t} + k x)$

Los valores de los parámetros son: masa inicial m₀=1 kg, flujo de arena c=0.001 kg/s, constante del muelle k=10 N/m, constante de proporcionalidad de la fuerza de rozamiento λ=0.05 kg/s. La posición inicial en el instante t=0, es x₀=0.1 m, y parte del reposo (dx/dt)₀=0

Resolvemos la ecuación diferencial hasta el instante t_f=100 s, la masa final es m=1-0.001·100=0.9 kg

m0=1; %masa inicial
c=0.001; %flujo de areana
k=10; %constante del muelle
lambda=0.05; %rozamiento
tf=100; %instante final

f=@(t,x) [x(2);(-lambda*x(2)-k*x(1))/(m0-c*t)]; 
[t,x]=ode45(f,[0,tf],[0.1,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('oscilador variable amortiguado')

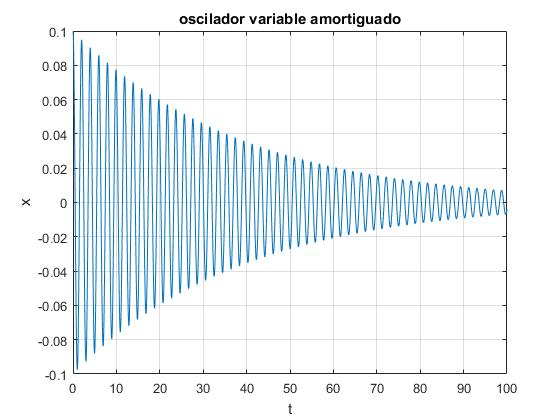
Observamos que la amplitud de la oscilación disminuye con el tiempo de forma similar a un oscilador amortiguado. Si el flujo de masa c es pequeño, la amplitud o envolvente A(t) es cóncava, similar a una exponencial decreciente

El periodo

El periodo P de las oscilaciones de una masa m sujeta al extremo libre de un muelle elástico k es

$P^{2} = 4 π^{2} \frac{m}{k}$

En el oscilador variable, la masa m cambia con el tiempo, por lo que el periodo P cambiará con el tiempo. En este apartado, vamos a representar el cuadrado del periodo P² en función de la masa m del depósito de arena, para comprobar si se mantiene la relación lineal

El periodo P de un oscilador es el intervalo de tiempo entre dos desplazamientos máximos. Definimos una función para señalar los máximos dx/dt=0 (velocidad nula, x>0) y obtener los instantes T_i de dichos máximos. Esta función se la pasamos al procedimiento ode45

function [detect,stopin,direction]=opcion2_ode45(~,x)
    detect=x(2); 
    stopin=0;
    direction=-1; 
end

Los valores de los parámetros son ahora los siguientes: masa inicial m₀=20 kg, flujo de arena c=0.2 kg/s, constante del muelle k=10 N/m, constante de proporcionalidad de la fuerza de rozamiento λ=0.05 kg/s. La posición inicial en el instante t=0, es x₀=0.1 m, y parte del reposo (dx/dt)₀=0

m0=20; %masa inicial
c=0.2; %flujo de areana
k=10; %constante del muelle
lambda=0.05; %rozamiento
tf=30; %instante final

f=@(t,x) [x(2);(-lambda*x(2)-k*x(1))/(m0-c*t)]; 
opts=odeset('events',@opcion2_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],[0.1,0],opts);
hold on
plot(t,x(:,1))
plot(te(ie==1),xe(ie==1),'o','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('x');
title('oscilador variable amortiguado')

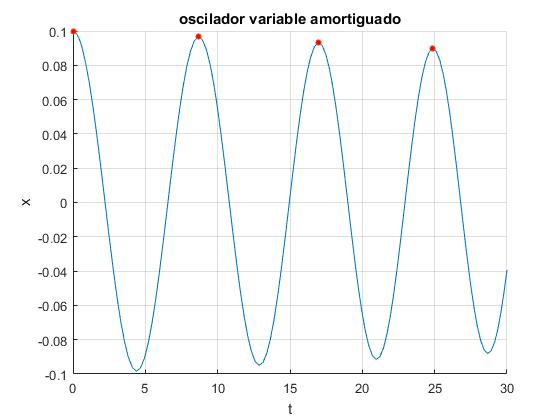
Los instantes en los que se producen los máximos desplazamientos (x>0) señalados por puntos de color rojo, se guardan en el vector

>> te(ie==1)
ans =
    0.0000
    8.6875
   16.9803
   24.8784

Supongamos que el osicilador parte del origen x=0, en el instante t=0, con velocidad no nula (dx/dt)₀≠0. El periodo es el intervalo de tiempo que transcurre entre dos pasos del móvil por el origen con velocidad positiva. Para ello definimos una función que se la pasamos al procedimiento ode45

function [detect,stopin,direction]=opcion1_ode45(~,x)
    detect=x(1); 
    stopin=0;
    direction=1; 
end

Modificamos el script anterior, cambiando solamente las condiciones iniciales

m0=20; %masa inicial
c=0.2; %flujo de areana
k=10; %constante del muelle
lambda=0.05; %rozamiento
tf=30; %instante final

f=@(t,x) [x(2);(-lambda*x(2)-k*x(1))/(m0-c*t)]; 
opts=odeset('events',@opcion1_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],[0,0.1*sqrt(k/m0)],opts);
hold on
plot(t,x(:,1))
plot(te(ie==1),xe(ie==1),'o','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('x');
title('oscilador variable amortiguado')

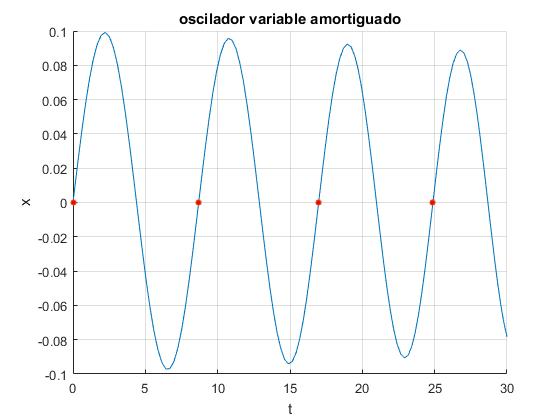
Los instantes en los que el móvil pasa por el origen con velocidad dx/dt>0 son

>> te(ie==1)
ans =
    0.0000
    8.6878
   16.9809
   24.8793

Guardamos estos instantes en el vector T, calculamos el periodo P como la diferencia T_i+1-T_i, al que hacemos corresponder la masa m en el instante ìntermedio (T_i+1+T_i)/2

Resolvemos la ecuación diferencial hasta el instante t_f=99.5 s, justamente, 0.5 s antes de que se acabe la arena en el depósito, con las condiciones iniciales, posición inicial es x₀=0.1 m, y parte del reposo (dx/dt)₀=0.

m0=20; %masa inicial
c=0.2; %flujo de areana
k=10; %constante del muelle
lambda=0.05; %rozamiento
tf=99.5; %instante final

f=@(t,x) [x(2);(-lambda*x(2)-k*x(1))/(m0-c*t)]; 
opts=odeset('events',@opcion2_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],[0.1,0],opts);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('oscilador variable amortiguado')

%periodos
T=te(ie==1);
P2=zeros(0, length(T));
m=zeros(0, length(T));

for i=1:length(T)-1
    P2(i)=(T(i+1)-T(i))^2; %cuadrado del periodo
    m(i)=m0-c*(T(i+1)+T(i))/2; %masa
end
figure
plot(m,P2, 'o','markersize',4,'markerfacecolor','r')
grid on
xlabel('m(t)')
ylabel('P^2');
title('oscilador variable amortiguado')

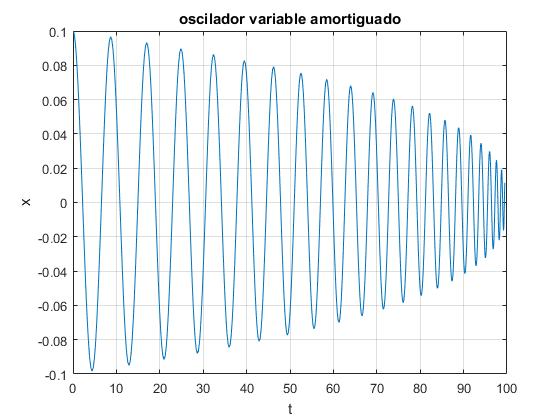
Observamos que la amplitud de la oscilación disminuye con el tiempo de forma completamente distinta a un oscilador amortiguado. Si el flujo de masa c es grande, la amplitud o envolvente A(t) es convexa.

Representamos el cuadrado de los periodos P² en función de la masa m(t) y comprobamos que los puntos se ajustan a una línea recta

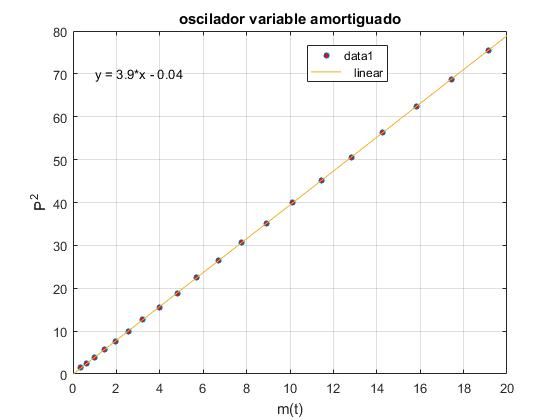
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. Observamos que hay una relación lineal entre el cuadrado del periodo P² y la masa variable del recipiente m

Solución analítica aproximada

En este apartado vamos a buscar una solución analítica aproximada de la ecuación diferencial del oscilador amortiguado con una masa que decrece linealmente con el tiempo m=m₀-ct

$m \frac{d^{2} x}{d t^{2}} + λ \frac{d x}{d t} + k x = 0$

Probamos una solución de la forma

$x (t) = A_{0} f (t) \sin (h (t) + φ)$

donde A₀ y φ se determinan a partir de las condiciones iniciales. f(t) y h(t) son funciones del tiempo a determinar

Calculamos las derivadas primera y segunda de x(t)

$\begin{array}{l} \frac{d x}{d t} = A_{0} \frac{d f}{d t} \sin (h + φ) + A_{0} f \frac{d h}{d t} \cos (h + φ) \\ \frac{d^{2} x}{d t^{2}} = A_{0} \frac{d^{2} f}{d t^{2}} \sin (h + φ) + A_{0} \frac{d f}{d t} \frac{d h}{d t} \cos (h + φ) + \\ A_{0} \frac{d f}{d t} \frac{d h}{d t} \cos (h + φ) + A_{0} f \frac{d^{2} h}{d t^{2}} \cos (h + φ) - A_{0} f {(\frac{d h}{d t})}^{2} \sin (h + φ) \end{array}$

Introducimos la solución x(t) y sus derivadas en la ecuación diferencial

$\begin{array}{l} {m (\frac{d^{2} f}{d t^{2}} - f {(\frac{d h}{d t})}^{2}) + λ \frac{d f}{d t} + k f} \sin (h + φ) + \\ {m (2 \frac{d f}{d t} \frac{d h}{d t} + f \frac{d^{2} h}{d t^{2}}) + λ f \frac{d h}{d t}} \cos (h + φ) = 0 \end{array}$

Igualando a cero los coeficientes del sin(h+φ) y de cos(h+φ), obtenemos un sistema de dos ecuaciones diferenciales

${\begin{cases} m (\frac{d^{2} f}{d t^{2}} - f {(\frac{d h}{d t})}^{2}) + λ \frac{d f}{d t} + k f = 0 \\ m (2 \frac{d f}{d t} \frac{d h}{d t} + f \frac{d^{2} h}{d t^{2}}) + λ f \frac{d h}{d t} = 0 \end{cases}$

En una primera aproximación, supondremos que la derivada primera df/dt y segunda d²f/dt² de la función f(t) en la primera ecuación diferencial son despreciables. De este modo, obtenemos una primera aproximación para la función h(t)

$\begin{array}{l} - m {(\frac{d h}{d t})}^{2} + k = 0 \\ \frac{d h}{d t} = \sqrt{\frac{k}{m (t)}} \\ \frac{d^{2} h}{d t^{2}} = \frac{c}{2 m} \frac{d h}{d t} \end{array}$

Introduciendo dh/dt y d²h/dt² en la segunda ecuación diferencial, obtenemos una expresión para f(t)

$\begin{array}{l} m (2 \frac{d f}{d t} \frac{d h}{d t} + f \frac{c}{2 m} \frac{d h}{d t}) + λ f \frac{d h}{d t} = 0 \\ 2 m \frac{d f}{d t} + (\frac{c}{2} + λ) f = 0 \\ (m_{0} - c t) \frac{d f}{d t} + \frac{1}{2} (\frac{c}{2} + λ) f = 0 \\ \ln \frac{f (t)}{f (0)} = (\frac{1}{4} + \frac{λ}{2 c}) \ln \frac{m_{0} - c t}{m_{0}} \\ f (t) = {(1 - \frac{c t}{m_{0}})}^{γ} γ = \frac{1}{4} + \frac{λ}{2 c} \end{array}$

Hemos supuesto que f(0)=1, y λ/(2c) representa el cociente entre el rozamiento y flujo de masa.

Conocido f(t), volvemos a la primera ecuación diferencial para obtener un valor aproximado de h(t), mejor que el que resultaría de la integración de la ecuación

$\frac{d h}{d t} = \sqrt{\frac{k}{m_{0} - c t}}$

Introducimos la expresión de f(t) y sus derivadas en la primera ecuación diferencial

$\begin{array}{l} m (\frac{d^{2} f}{d t^{2}} - f {(\frac{d h}{d t})}^{2}) + λ \frac{d f}{d t} + k f = 0 \\ m (γ (γ - 1) {(\frac{c}{m_{0}})}^{2} {(1 - \frac{c t}{m_{0}})}^{γ - 2} - {(1 - \frac{c t}{m_{0}})}^{γ} {(\frac{d h}{d t})}^{2}) - \\ λ γ \frac{c}{m_{0}} {(1 - \frac{c t}{m_{0}})}^{γ - 1} + k {(1 - \frac{c t}{m_{0}})}^{γ} = 0 \\ {(\frac{d h}{d t})}^{2} = \frac{k}{m} + \frac{c^{2} γ (γ - 1) - λ c γ}{m^{2}} \\ {(\frac{d h}{d t})}^{2} = \frac{k}{m} - \frac{(\frac{c}{2} + λ) (\frac{3 c}{2} + λ)}{4 m^{2}} \end{array}$

Sabiendo que m=m₀-ct, y tomando h(0)=0, la integral es

$\begin{array}{l} h (t) - h (0) = \int_{0}^{t} \sqrt{\frac{k}{(m_{0} - c t)} - \frac{(\frac{c}{2} + λ) (\frac{3 c}{2} + λ)}{4 {(m_{0} - c t)}^{2}}} d t = - \frac{\sqrt{k}}{c} \int_{0}^{t} \frac{\sqrt{u - a}}{u} d u \\ u = m_{0} - c t a = \frac{(\frac{c}{2} + λ) (\frac{3 c}{2} + λ)}{4 k} \end{array}$

Para resolver la integral se hace el cambio z²=u-a

$\int \frac{\sqrt{u - a}}{u} d u = 2 \int \frac{z^{2}}{z^{2} + a} = 2 (z - \sqrt{a} \arctan \frac{z}{\sqrt{a}})$

Deshaciendo los cambios, una mejor aproximación para la función h(t) es

$\begin{array}{l} h (t) = {\frac{2}{c} \sqrt{k a} (\arctan \sqrt{\frac{m_{0} - c t - a}{a}} - \sqrt{\frac{m_{0} - c t - a}{a}}) |}_{0}^{t} \\ h (t) = \frac{2}{c} \sqrt{k a} (\arctan \sqrt{\frac{m_{0} - c t - a}{a}} - \sqrt{\frac{m_{0} - c t - a}{a}} - \arctan \sqrt{\frac{m_{0} - a}{a}} + \sqrt{\frac{m_{0} - a}{a}}) \end{array}$

Esta solución es válida siempre que se cumpla que a<m₀-ct.

La amplitud

Examinamos el signo de la derivada segunda de la amplitud, A₀f(t), lo que nos da la concavidad de la envolvente de la oscilación

$\frac{d^{2} A}{d t^{2}} = A_{0} γ (γ - 1) {(\frac{c}{m_{0}})}^{2} {(1 - \frac{c t}{m_{0}})}^{γ - 2}$

Cuando γ=1, la derivada segunda es cero y la amplitud decrece linealmente con el tiempo
Cuando γ>1, el decrecimiento de la amplitud es similar al de las oscilaciones amortiguadas, la envolvente es cóncava
Cuando γ<1, la envolvente es convexa

Vamos a respresentar las oscilaciones de este sistema de masa variable para los tres casos.

La ecuación del movimiento es

$\begin{array}{l} x (t) = A_{0} f (t) \sin (h (t) + φ) \\ \frac{d x}{d t} = A_{0} \frac{d f}{d t} \sin (h (t) + φ) + A_{0} f (t) \frac{d h}{d t} \cos (h (t) + φ) \end{array}$

Dadas las condiciones iniciales x₀ y (dx/dt)₀, determinamos la amplitud A₀ y la fase inicial φ

$\begin{array}{l} x_{0} = A_{0} \sin φ \\ {(\frac{d x}{d t})}_{0} = - \frac{c}{m_{0}} γ A_{0} \sin φ + \sqrt{\frac{k}{m_{0}} - \frac{k a}{m_{0}^{2}}} A_{0} \cos φ \end{array}$

γ<1

m0=20; %masa inicial
c=0.2; %flujo de arena
k=10; %constante del muelle
lambda=0.05; %rozamiento
x0=0.1;  %velocidad inicial cero
tf=99.5; %hasta el tiempo

gamma=lambda/(2*c)+1/4;
a=(c/2+lambda)*(3*c/2+lambda)/(4*k);
%condiciones iniciales
A0_s=x0;
A0_c=c*gamma*x0/(m0*sqrt(k/m0-k*a/m0^2));
A0=sqrt(A0_s^2+A0_c^2);
phi=atan2(A0_s,A0_c);

h=@(t) 2*sqrt(k*a)*(atan(sqrt((m0-c*t-a)/a))-sqrt((m0-c*t-a)/a)
-atan(sqrt((m0-a)/a))+sqrt((m0-a)/a))/c;
A=@(t) A0*(1-c*t/m0).^gamma;
x=@(t) A(t).*sin(h(t)+phi);
hold on
fplot(x,[0,tf])
fplot(A,[0,tf]) %envolvente
hold off
grid on
xlabel('t')
ylabel('x')
title('Oscilador variable amortiguado')

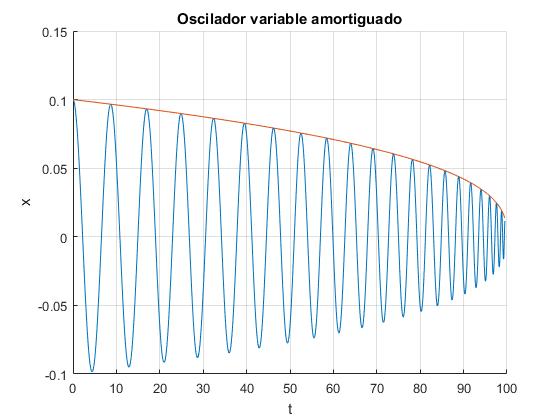
gamma =    0.3750

γ>1

Los valores de los parámetros son ahora los siguientes: masa inicial m₀=1 kg, flujo de arena c=0.001 kg/s, constante del muelle k=10 N/m, constante de proporcionalidad de la fuerza de rozamiento λ=0.05 kg/s. La posición inicial en el instante t=0, es x₀=0.1 m, y parte del reposo (dx/dt)₀=0

m0=1; %masa inicial
c=0.001; %flujo de arena
k=10; %constante del muelle
lambda=0.05; %rozamiento
x0=0.1;  %velocidad inicial cero
tf=100; %hasta el tiempo
...

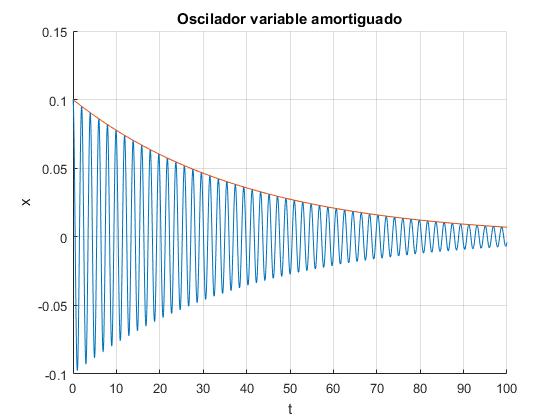
gamma =    25.2500

γ=1

Dado que el coeficiente $γ = \frac{1}{4} + \frac{λ}{2 c}$ , para que γ=1, entonces c=2λ/3

Los valores de los parámetros son ahora los siguientes: masa inicial m₀=1 kg, constante del muelle k=10 N/m, constante de proporcionalidad de la fuerza de rozamiento λ=0.05 kg/s, flujo de arena c=0.1/3 kg/s. La posición inicial en el instante t=0, es x₀=0.1 m, y parte del reposo (dx/dt)₀=0

m0=1; %masa inicial
k=10; %constante del muelle
lambda=0.05; %rozamiento
c=2*lambda/3; %flujo de arena
x0=0.1;  %velocidad inicial cero
tf=27; %hasta el tiempo
...

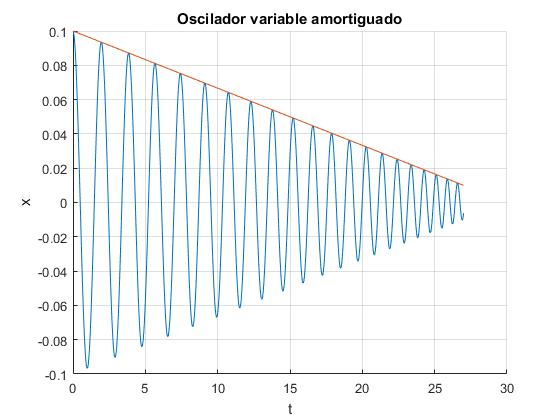
gamma =    1

Periodo

La ecuación del movimiento es

$x (t) = A_{0} f (t) \sin (h (t) + φ)$

Cuando la fase (argumento del seno) se incrementa en 2π el tiempo se incrementa en un periodo P

h(t+P)=h(t)+2π

$h (t + P) - h (t) = \frac{2}{c} \sqrt{k a} {\begin{cases} \arctan \sqrt{\frac{m_{0} - c (t + P) - a}{a}} - \sqrt{\frac{m_{0} - c (t + P) - a}{a}} \\ - \arctan \sqrt{\frac{m_{0} - c t - a}{a}} + \sqrt{\frac{m_{0} - c t - a}{a}} \end{cases}}$

Comenzamos con t=0, resolvemos la ecuación trascendente, h(P)-h(0)=2π, para calcular el primer periodo P₁, al que asignamos la masa m₁=m₀-cP₁/2, de un tiempo intermedio entre 0 y P₁.

Ahora ponemos t=P₁, resolvemos la ecuación trascendente h(P₁+P)-h(P₁)=2π, para calcular el segundo periodo P₂ al que asignamos la masa m₂=m₀-c(P₁+P₂/2), de un tiempo intermedio entre P₁ y P₁+P₂ y así, sucesivamente

Representamos en el eje horizontal el vector m de la masa y en el eje vertical el cuadrado de los periodos P² y comprobamos que son proporcionales, se ajustan a una línea recta, tal como mostramos en la sección anterior

m0=20; %masa inicial
c=0.2; %flujo de arena
k=10; %constante del muelle
lambda=0.05; %rozamiento

gamma=lambda/(2*c)+1/4;
a=(c/2+lambda)*(3*c/2+lambda)/(4*k);

h=@(t) 2*sqrt(k*a)*(atan(sqrt((m0-c*t-a)/a))-sqrt((m0-c*t-a)/a))/c;
N=10; %número de periodos
P=zeros(0,N);
m=zeros(0,N);
t0=0;
for i=1:N
    f=@(x) h(t0+x)-h(t0)-2*pi;
    p_a=2*pi*sqrt((m0-c*t0)/k);
    P(i)=fzero(f,p_a); %calcula el periodo
    m(i)=m0-c*(t0+P(i)/2);
    t0=t0+P(i);
end
plot(m,T.^2,'o','markersize',4,'markerfacecolor','r')
grid on
xlabel('m(t)')
ylabel('P^2');
title('oscilador variable amortiguado')

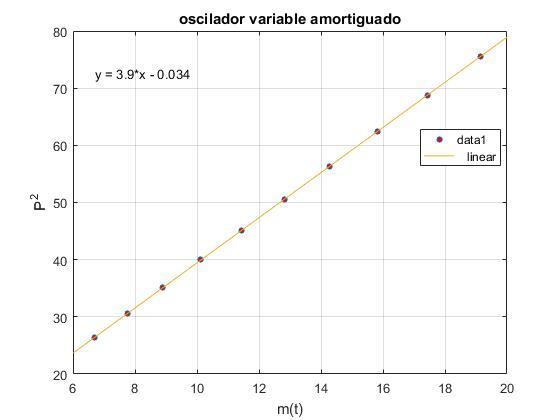
Energía del oscilador

La energía del oscilador, es la suma de la energía cinética de la masa variable m que se mueve con velocidad dx/dt y de la energía potencial del muelle elástico kx²/2.

La energía del oscilador disminuye con el tiempo debido al trabajo de la fuerza de rozamiento y a la pérdida de masa que experimenta el sistema

$\begin{array}{l} \frac{d E_{k}}{d t} = \frac{1}{2} \frac{d m}{d t} {(\frac{d x}{d t})}^{2} + m \frac{d x}{d t} \frac{d^{2} x}{d t^{2}} \\ \frac{d E_{p}}{d t} = k x \frac{d x}{d t} \\ \frac{d (E_{k} + E_{p})}{d t} = - (\frac{c}{2} + λ) {(\frac{d x}{d t})}^{2} \end{array}$

Vamos a estimar la pérdida aproximada de energía del oscilador en la unidad de tiempo. Para un oscilador libre (sin rozamiento y masa constante), la posición, velocidad y energía son, respectivamente

$\begin{array}{l} x = A \sin (ω t + φ) \\ \frac{d x}{d t} = A ω \cos (ω t + φ) \\ E_{k} + E_{p} = \frac{1}{2} k A^{2} \end{array}$

El periodo P=2π/ω y ω²=k/m

Sabiendo que el valor medio de una función periódica f(t) de periodo P es

$< f (t) > = \frac{1}{P} \int_{0}^{P} f (t) d t$

Por tanto, el valor medio del cuadrado de la velocidad de la partícula es

$〈 {(\frac{d x}{d t})}^{2} 〉 = \frac{2}{P} \int_{0}^{P / 2} A^{2} ω^{2} \cos^{2} (ω t + φ) d t = \frac{2}{P} A^{2} ω^{2} \int_{0}^{P / 2} \frac{1 + \cos 2 (ω t + φ)}{2} d t = \frac{1}{2} A^{2} ω^{2}$

Recuérdese que el periodo de cosx es 2π, sin embargo, el periodo de cos²x es π (la mitad)

La pérdida de energía del oscilador en la unidad de tiempo es aproximadamente

$\frac{d (E_{k} + E_{p})}{d t} \approx - (\frac{c}{2} + λ) \frac{1}{2} \frac{k}{m (t)} A^{2} (t)$

Como E_k+E_p=kA²/2. Integramos la ecuación diferencial para obtener una expresión aproximada para la amplitud A(t), sabiendo que en el instante t=0, A=A₀ y m=m₀

$\begin{array}{l} \frac{d A (t)}{d t} = - \frac{1}{2} (\frac{c}{2} + λ) \frac{A (t)}{m (t)} \\ \int_{0}^{t} \frac{d A}{A} = - \frac{1}{2} (\frac{c}{2} + λ) \int_{0}^{t} \frac{d t}{m_{0} - c t} \\ A = A_{0} {(1 - \frac{c t}{m_{0}})}^{γ} γ = \frac{1}{4} + \frac{λ}{2 c} \end{array}$

El mismo resultado que hemos obtenido el principio de este apartado A(t)=A₀f(t)

Actividades

Se introduce

La masa inicial m₀ del depósito de arena en kg, en el control titulado Masa inicial
El flujo de arena c en kg/s, en el control titulado Flujo

El resto de los parámetros están fijados en el programa interactivo

La constante del muelle elástico, k=10 N/m
La constante λ=0.05 kg/s de la fuerza de rozamiento proporcional a la velocidad
La posición inicial del depósito lleno de arena es x₀=0.1 m y parte del reposo (dx/dt)₀=0

Se representa el muelle y el recipiente con arena en color azul claro. En la parte derecha se representa, la posición del depósito en función del tiempo. Un segundo antes de que el recipiente se vacíe, es decir, su masa m sea cero, se detiene el programa, para evitar divisiones entre cero.

En la parte superior, se proporcionan los datos del tiempo t, posición x y velocidad dx/dt

Flujo c Masa inicial m₀

Referencias

José Flores, Guillermo Solovey, Salvador Gil. Variable mass oscillator. Am. J. Phys. 71 (7) July 2003, pp. 721-725

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 11.29, 11.30, pp. 385-390