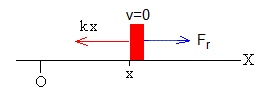
Cuando el bloque se encuentra en reposo, actúan dos fuerzas iguales y de sentido contrario sobre el mismo:

• La que ejerce el muelle, proporcional a su deformación kx, donde k es la constante elástica
• La fuerza de rozamiento F_r, que deberá ser inferior a su máximo valor μ_smg. Donde μ_s es el coeficiente estático.

Cuando la fuerza que ejerce el muelle kx es mayor o igual que μ_smg, el cuerpo empieza a deslizar sobre el plano horizontal. El bloque incrementa su velocidad, actuando la fuerza de rozamiento proporcional a la velocidad λv

Supongamos que el bloque parte de la posición x₀, y se cumple que k|x₀|>μ_smg, vamos a estudiar el movimiento del bloque hasta que se detiene después de un tiempo

Primer periodo

Estudiamos por separado el movimiento hacia la izquierda y a continuación, si no se detiene, hacia la derecha

Movimiento hacia la izquierda

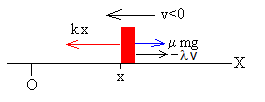
Cuando el bloque se mueve hacia la izquierda (v<0), la ecuación del movimiento es

ma=-kx+μmg+(-λv)

En forma de ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\mu g\frac{dx}{dt}<0\hfill \\ 2\gamma =\frac{\lambda }{m}{\omega }_0^2=\frac{k}{m}\hfill \end{array}}$

μ es el coeficiente cinético, ω₀ es la frecuencia natural o propia del oscilador, γ es el coeficiente de amortiguamiento

La solución particular de la ecuación diferencial es, x₁=C, donde C es una constante a determinar introduciéndola en la ecuación diferencial

${\displaystyle C=\frac{\mu g}{{\omega }_0^2}}$

La solución de la homogénea es la deducida en la página titulada oscilaciones amortiguadas

${\displaystyle x_2=\exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)}$

La solución completa es x=x₁+x₂

${\displaystyle \begin{array}{l}x=\exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)+\frac{\mu g}{{\omega }_0^2}\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

ω se denomina frecuencia de la oscilación amortiguada, que difiere poco de la frecuencia natura ω₀ si el amortiguamiento γ es pequeño

La velocidad del bloque es

${\displaystyle \begin{array}{l}v=\frac{dx}{dt}=-\gamma \left(A\sin (\omega t)+B\right)+\omega \exp (-\gamma t)\left(A\cos (\omega t)-B\sin (\omega t)\right)=\\ \exp (-\gamma t)\left\{\left(\omega A-\gamma B\right)\cos (\omega t)-\left(\gamma A+\omega B\right)\sin (\omega t)\right\}\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: el bloque parte de la posición x₀ en el instante t=0, en reposo, v=0 si se cumple que k|x₀|>μ_smg, o bien ${\omega }_0^2\left|x_0\right|>{\mu }_{s}g$

El resultado es

${\displaystyle \begin{array}{l}B=x_0-\frac{\mu g}{{\omega }_0^2}\\ A=\frac{\gamma }{\omega }B\end{array}}$

Para simplificar la notación denominaremos, $\Delta x=\frac{\mu g}{{\omega }_0^2}$

La posición del bloque desde el momento en que se suelta t=0, es

${\displaystyle x=\exp (-\gamma t)\left(x_0-\Delta x\right)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)+\Delta x}$

y su velocidad

${\displaystyle v=\frac{dx}{dt}=-\frac{{\omega }_0^2}{\omega }\left(x_0-\Delta x\right)\exp (-\gamma t)\sin (\omega t)}$

Se detiene cuando v=0, o cuando ωt=π, en la posición

${\displaystyle x_1=-\exp \left(-\gamma \frac{\pi }{\omega }\right)\left(x_0-\Delta x\right)+\Delta x}$

Para simplificar la notación denominaremos, $\beta =\exp \left(-\gamma \frac{\pi }{\omega }\right)$

La posición final x₁ se escribe con la notación establecida

${\displaystyle x_1=-\beta x_0+\left(\beta +1\right)\Delta x}$

Movimiento hacia la derecha

Si se cumple que ${\omega }_0^2\left|x_1\right|>{\mu }_{s}g$ el bloque se mueve hacia la derecha

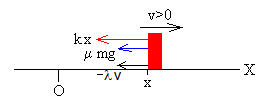
Cuando el bloque se mueve hacia la derecha (v>0), la ecuación del movimiento es

ma=-kx-μmg-λv

En forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=-\mu g\frac{dx}{dt}>0}$

La solución completa para t>π/ω es

${\displaystyle x=\exp \left(-\gamma \left(t-\frac{\pi }{\omega }\right)\right)\left(A\sin \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)+B\cos \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)\right)-\frac{\mu g}{{\omega }_0^2}}$

La velocidad del bloque cuando se mueve hacia la derecha es

${\displaystyle v=\frac{dx}{dt}=\exp \left(-\gamma \left(t-\frac{\pi }{\omega }\right)\right)\left\{\left(\omega A-\gamma B\right)\cos \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)-\left(\gamma A+\omega B\right)\sin \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)\right\}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, el móvil parte de la posición x₁ en el instante t=π/ω, en reposo, v=0, si se cumple que ${\omega }_0^2\left|x_1\right|>{\mu }_{s}g$

El resultado es

${\displaystyle \begin{array}{l}B=x_1+\Delta x\\ A=\frac{\gamma }{\omega }B\end{array}}$

La posición y velocidad en función del tiempo para t>π/ω es

${\displaystyle \begin{array}{l}x=\left(x_1+\Delta x\right)\exp \left(-\gamma \left(t-\frac{\pi }{\omega }\right)\right)\left(\frac{\gamma }{\omega }\sin \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)+\cos \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)\right)-\Delta x\\ v=\frac{dx}{dt}=-\frac{{\omega }_0^2}{\omega }\left(x_1+\Delta x\right)\exp \left(-\gamma \left(t-\frac{\pi }{\omega }\right)\right)\sin \left(\omega \left(t-\frac{\pi }{\omega }\right)\right)\end{array}}$

El bloque se detiene v=0, en el instante t=2π/ω, en la posición x₂

${\displaystyle x_2=-\left(x_1+\Delta x\right)\beta -\Delta x={\beta }^2{x}_0-({\beta }^2+2\beta +1)\Delta x}$

Segundo periodo

Movimiento hacia la izquierda

Si se cumple que ${\omega }_0^2\left|x_2\right|>{\mu }_{s}g$ el bloque se mueve hacia la izquierda

La posición del bloque para t>2π/ω es

${\displaystyle x=\exp \left(-\gamma \left(t-\frac{2\pi }{\omega }\right)\right)\left(A\sin \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)+B\cos \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)\right)+\frac{\mu g}{{\omega }_0^2}}$

Derivando obtenemos su velocidad

${\displaystyle v=\frac{dx}{dt}=\exp \left(-\gamma \left(t-\frac{2\pi }{\omega }\right)\right)\left\{\left(\omega A-\gamma B\right)\cos \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)-\left(\gamma A+\omega B\right)\sin \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)\right\}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, el móvil parte de la posición x₂ en el instante t=2π/ω, en reposo, v=0, si se cumple que ${\omega }_0^2\left|x_2\right|>{\mu }_{s}g$

El resultado es

${\displaystyle \begin{array}{l}B=x_2-\Delta x\\ A=\frac{\gamma }{\omega }B\end{array}}$

La posición y velocidad del bloque en función del tiempo, para t>2π/ω es

${\displaystyle \begin{array}{l}x=\left(x_2-\Delta x\right)\exp \left(-\gamma \left(t-\frac{2\pi }{\omega }\right)\right)\left(\frac{\gamma }{\omega }\sin \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)+\cos \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)\right)+\Delta x\\ v=\frac{dx}{dt}=-\frac{{\omega }_0^2}{\omega }\left(x_2-\Delta x\right)\exp \left(-\gamma \left(t-\frac{2\pi }{\omega }\right)\right)\sin \left(\omega \left(t-\frac{2\pi }{\omega }\right)\right)\end{array}}$

El bloque se detiene v=0, en el instante t=3π/ω, en la posición x₃

${\displaystyle x_3=-\beta \left(x_2-\Delta x\right)+\Delta x=-{\beta }^3{x}_0+\left({\beta }^3+2{\beta }^2+2\beta +1\right)\Delta x}$

Movimiento hacia la derecha

Si se cumple que ${\omega }_0^2\left|x_3\right|>{\mu }_{s}g$ el bloque se mueve hacia la derecha

La posición del bloque para t>3π/ω es

${\displaystyle x=\exp \left(-\gamma \left(t-\frac{3\pi }{\omega }\right)\right)\left(A\sin \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)+B\cos \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)\right)-\frac{\mu g}{{\omega }_0^2}}$

Derivando, obtenemos su velocidad

${\displaystyle v=\frac{dx}{dt}=\exp \left(-\gamma \left(t-\frac{3\pi }{\omega }\right)\right)\left\{\left(\omega A-\gamma B\right)\cos \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)-\left(\gamma A+\omega B\right)\sin \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)\right\}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, el móvil parte de la posición x₃ en el instante t=3π/ω, en reposo, v=0, si se cumple que ${\omega }_0^2\left|x_3\right|>{\mu }_{s}g$

El resultado es

${\displaystyle \begin{array}{l}B=x_3+\Delta x\\ A=\frac{\gamma }{\omega }B\end{array}}$

La posición y velocidad del bloque en función del tiempo, para t>3π/ω es

${\displaystyle \begin{array}{l}x=\left(x_3+\Delta x\right)\exp \left(-\gamma \left(t-\frac{3\pi }{\omega }\right)\right)\left(\frac{\gamma }{\omega }\sin \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)+\cos \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)\right)-\Delta x\\ v=\frac{dx}{dt}=-\frac{{\omega }_0^2}{\omega }\left(x_3+\Delta x\right)\exp \left(-\gamma \left(t-\frac{3\pi }{\omega }\right)\right)\sin \left(\omega \left(t-\frac{3\pi }{\omega }\right)\right)\end{array}}$

El bloque se detiene v=0, en el instante t=4π/ω, en la posición x₄

${\displaystyle x_4=-\beta \left(x_3+\Delta x\right)-\Delta x={\beta }^4{x}_0-\left({\beta }^4+2{\beta }^3+2{\beta }^2+2\beta +1\right)\Delta x}$

Generalización

Sea x₀, la posición de partida y P=2π/ω el periodo. Las posiciones del bloque en los instantes t=nP/2 en los que se encuentra en reposo v=0, son

${\displaystyle \begin{array}{l}n=1x\left(1\frac{P}{2}\right)=-\beta x_0+\left(\beta +1\right)\Delta x\\ n=2x\left(2\frac{P}{2}\right)={\beta }^2{x}_0-({\beta }^2+2\beta +1)\Delta x\\ n=3x\left(3\frac{P}{2}\right)=-{\beta }^3{x}_0+\left({\beta }^3+2{\beta }^2+2\beta +1\right)\Delta x\\ n=4x\left(4\frac{P}{2}\right)={\beta }^4{x}_0-\left({\beta }^4+2{\beta }^3+2{\beta }^2+2\beta +1\right)\Delta x\\ \mathrm{....}\\ x\left(n\frac{P}{2}\right)={\left(-1\right)}^n\left\{{\beta }^n{x}_0-\left({\beta }^n+2{\beta }^{n-1}+\mathrm{...}+2{\beta }^2+2\beta +1\right)\Delta x\right\}\end{array}}$

Observamos que las potencias de β multiplicados por 2 forman una progresión geométrica, cuya suma es

${\displaystyle \begin{array}{l}{\beta }^n+2{\beta }^{n-1}+\mathrm{...}+2{\beta }^2+2\beta +1={\beta }^n+2\beta \left({\beta }^{n-2}+{\beta }^{n-3}+\mathrm{...}+\beta +1\right)+1=\\ {\beta }^n+2\beta \frac{1-{\beta }^{n-1}}{1-\beta }+1=\frac{\left(1+\beta \right)\left(1-{\beta }^n\right)}{1-\beta }\end{array}}$

La expresión del término gneral x(nP/2) es

${\displaystyle x\left(n\frac{P}{2}\right)={\left(-1\right)}^n\left\{{\beta }^n{x}_0-\frac{\left(1+\beta \right)\left(1-{\beta }^n\right)}{1-\beta }\Delta x\right\}}$

Consideremos el siguiente oscilador

• Frecuencia propia ${\omega }_0=\sqrt{50}$ rad/s
• Constante de amortiguamiento, γ=0.1 s^-1
• Coeficiente cinético y estático μ=0.2

El script proporciona las posiciones en las que el bloque se encuentra en reposo v=0 en los instantes nP/2 o bien, nπ/ω

w0=sqrt(50); %frecuencia propia
gamma=0.1; %constante de amortiguamiento
w=sqrt(w0^2-gamma^2); %frecuencia de la oscilacón amortiguada
mu=0.2; %coeficiente estático y cinético
Dx=9.8*mu/w0^2;
beta=exp(-gamma*pi/w);
x0=0.7; %posición inicial

n=0;
while(1)
    x=(-1)^n*(beta^n*x0-(1+beta)*(1-beta^n)*Dx/(1-beta));
    if w0^2*abs(x)<mu*9.8
        break
    end
    disp([n, n*pi/w,x])
    n=n+1;
end

         0         0    0.7000
    1.0000    0.4443   -0.5929
    2.0000    0.8887    0.4904
    3.0000    1.3330   -0.3924
    4.0000    1.7773    0.2987
    5.0000    2.2217   -0.2090
    6.0000    2.6660    0.1232
    7.0000    3.1103   -0.0412

Las posiciones y velocidades en función del tiempo en los sucesivos semiperiodos son

${\displaystyle \begin{array}{l}0-1\frac{P}{2}\{\begin{array}{l}x=\exp (-\gamma t)\left(x_0-\Delta x\right)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)+\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_0-\Delta x\right)\exp (-\gamma t)\sin (\omega t)\end{array}\\ 1\frac{P}{2}-2\frac{P}{2}\{\begin{array}{l}x=\left(x_1+\Delta x\right)\frac{1}{\beta }\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t-\pi \right)+\cos \left(\omega t-\pi \right)\right)-\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_1+\Delta x\right)\frac{1}{\beta }\exp \left(-\gamma t\right)\sin \left(\omega t-\pi \right)\end{array}\\ 2\frac{P}{2}-3\frac{P}{2}\{\begin{array}{l}x=\left(x_2-\Delta x\right)\frac{1}{{\beta }^2}\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t-2\pi \right)+\cos \left(\omega t-2\pi \right)\right)+\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_2-\Delta x\right)\frac{1}{{\beta }^2}\exp \left(-\gamma t\right)\sin \left(\omega t-2\pi \right)\end{array}\\ 3\frac{P}{2}-4\frac{P}{2}\{\begin{array}{l}x=\left(x_3+\Delta x\right)\frac{1}{{\beta }^3}\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t-3\pi \right)+\cos \left(\omega t-3\pi \right)\right)-\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_3+\Delta x\right)\frac{1}{{\beta }^3}\exp \left(-\gamma t\right)\sin \left(\omega t-3\pi \right)\end{array}\\ \mathrm{...}\\ n\frac{P}{2}-(n+1)\frac{P}{2}\{\begin{array}{l}x=\left(x_n-{\left(-1\right)}^n\Delta x\right)\frac{1}{{\beta }^n}\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t-n\pi \right)+\cos \left(\omega t-n\pi \right)\right)+{\left(-1\right)}^n\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_n-{\left(-1\right)}^n\Delta x\right)\frac{1}{{\beta }^n}\exp \left(-\gamma t\right)\sin \left(\omega t-n\pi \right)\end{array}\end{array}}$

Introduciendo la expresión de x_n o x(nP/2) en el término general, obtenemos

${\displaystyle \begin{array}{l}n\frac{P}{2}-(n+1)\frac{P}{2}\{\begin{array}{l}x={\left(-1\right)}^n\left\{\left(x_0-\Delta x\frac{2{\beta }^{-n}-\beta -1}{1-\beta }\right)\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t\right)+\cos \left(\omega t\right)\right)\cos (n\pi )+\Delta x\right\}\\ v=-\frac{{\omega }_0^2}{\omega }{\left(-1\right)}^n\left(x_0-\Delta x\frac{2{\beta }^{-n}-\beta -1}{1-\beta }\right)\exp \left(-\gamma t\right)\sin \left(\omega t\right)\cos (n\pi )\end{array}\\ n\frac{P}{2}-(n+1)\frac{P}{2}\{\begin{array}{l}x=\left(x_0-\Delta x\frac{2{\beta }^{-n}-\beta -1}{1-\beta }\right)\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t\right)+\cos \left(\omega t\right)\right)+{\left(-1\right)}^n\Delta x\\ v=-\frac{{\omega }_0^2}{\omega }\left(x_0-\Delta x\frac{2{\beta }^{-n}-\beta -1}{1-\beta }\right)\exp \left(-\gamma t\right)\sin \left(\omega t\right)\end{array}\end{array}}$

hemos utilizado cos(nπ)=(-1)ⁿ y sin(nπ)=0

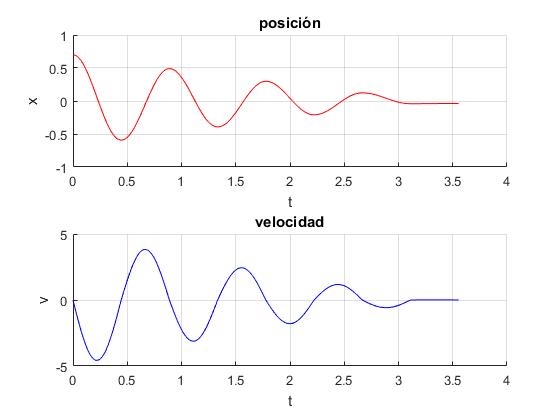
El script representa la posición x y velocidad x en función del tiempo t. Con la herramienta del menú de la ventana gráfica Data cursor podemos medir las posiciones en las que el bloque se encuentra en reposo v=0

w0=sqrt(50); %frecuencia propia
gamma=0.1; %constante de amortiguamiento
w=sqrt(w0^2-gamma^2); %frecuencia de la oscilación amortiguada
mu=0.2; %coeficiente estático y cinético
Dx=9.8*mu/w0^2;
beta=exp(-gamma*pi/w);
x0=0.7; %posición inicial
subplot(2,1,1)

n=0;
hold on
while(1)
    x=@(t) (x0-Dx*(2*beta^(-n)-beta-1)/(1-beta))*exp(-gamma*t).*(gamma*sin(w*t)/w
+cos(w*t))+(-1)^n*Dx;
    if w0^2*abs(x(n*pi/w))<mu*9.8
        break
    end
    fplot(x,[n*pi/w,(n+1)*pi/w],'r')
    n=n+1;
end
hold off
grid on
xlabel('t')
ylabel('x')
title('posición')
subplot(2,1,2)
n=0;
hold on
while(1)
    x=@(t) (x0-Dx*(2*beta^(-n)-beta-1)/(1-beta))*exp(-gamma*t).*(gamma*sin(w*t)/w
+cos(w*t))+(-1)^n*Dx;
    v=@(t) -w0^2*(x0-Dx*(2*beta^(-n)-beta-1)/(1-beta))*exp(-gamma*t).*sin(w*t)/w;
    if w0^2*abs(x(n*pi/w))<mu*9.8
        break
    end
    fplot(v,[n*pi/w,(n+1)*pi/w],'b')
    n=n+1;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('velocidad')

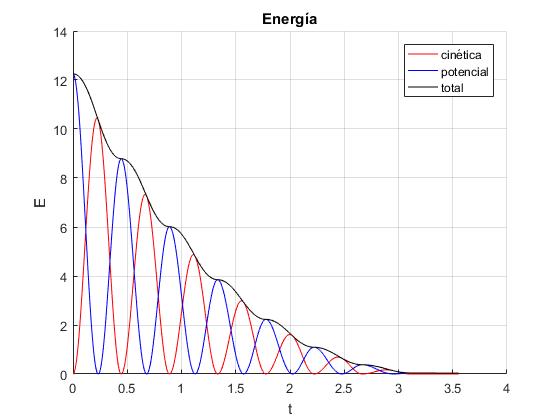
Representamos la energía cinética, E_k=v²/2, potencial $E_p=\frac{1}{2}{\omega }_0^2{x}^2$ y total

w0=sqrt(50); %frecuencia propia
gamma=0.1; %constante de amortiguamiento
w=sqrt(w0^2-gamma^2); %frecuencia de la oscilacón amortiguada
mu=0.2; %coeficiente estático y cinético
Dx=9.8*mu/w0^2;
beta=exp(-gamma*pi/w);
x0=0.7; %posición inicial
hold on
n=0;
while(1)
    x=@(t) (x0-Dx*(2*beta^(-n)-beta-1)/(1-beta))*exp(-gamma*t).*(gamma*sin(w*t)/w
+cos(w*t))+(-1)^n*Dx;
    v=@(t) -w0^2*(x0-Dx*(2*beta^(-n)-beta-1)/(1-beta))*exp(-gamma*t).*sin(w*t)/w;
    if w0^2*abs(x(n*pi/w))<mu*9.8
        break
    end
    Ek=@(t) v(t).^2/2;
    Ep=@(t) w0^2*x(t).^2/2;
    E=@(t) Ek(t)+Ep(t);
    fplot(Ek,[n*pi/w,(n+1)*pi/w],'r')
    fplot(Ep,[n*pi/w,(n+1)*pi/w],'b')
    fplot(E,[n*pi/w,(n+1)*pi/w],'k')
    n=n+1;
end
hold off
grid on
legend('cinética','potencial','total')
xlabel('t')
ylabel('E')
title('Energía')

Actividades

Se introduce

• El coeficiente de rozamiento μ en el control titulado Coef. rozamiento
• El coeficiente de amortiguamiento, γ, el control titulado Amortiguamiento
• La constante elástica k del muelle  o cuadrado de la frecuencia angular ω₀, en el control titulado Constante elástica.
• La posición inicial del bloque en el control titulado Posición inicial
• La masa del bloque se ha fijado en m=1.0 kg

Se pulsa el botón titulado Nuevo

Se observa el movimiento del bloque entre los puntos de retorno, hasta que se para.

Se representa la posición del bloque en función del tiempo.

• Una flecha de color rojo, representa la fuerza que ejerce el muelle
• Una flecha de color azul, representa la fuerza de rozamiento constante.
• Una flecha de color negro, representa la fuerza de rozamiento proporcional a la velocidad.

En la parte superior derecha, se proporcionan los datos de

• El tiempo
• La posición del bloque
• La velocidad del bloque
• La energía del bloque (cinética más potencial)

En la parte izquierda, se representa la energía del bloque en forma de diagrama de barras.

• En color rojo, la energía potencial elástica
• En color azul, la energía cinética

vemos como la energía total disminuye continuamente a causa del trabajo de las fuerzas de rozamiento.

Referencias

Peter F. Hinrichsen, Chris I. Larnder. Combined viscous and dry friction damping of oscillatory motion. Am. J. Phys. 86 (8) August 2018, pp 577-584