Estudiamos ahora, el péndulo simple cuyo comportamiento difiere del oscilador consistente en una masa unida a un muelle elástico

Cuando un péndulo simple oscila en el aire, es una suposición razonable considerar que la fuerza de rozamiento que actúa sobre la partícula sea proporcional al cuadrado de la velocidad.

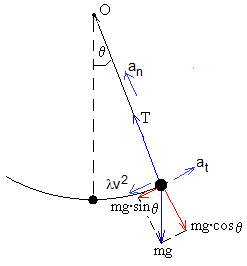
El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l (la longitud del péndulo).

Las fuerzas que actúan sobre la partícula de masa m son:

• el peso mg
• La tensión T del hilo
• La fuerza de rozamiento λv² de signo contrario a la velocidad v

• Movimiento en la dirección radial

La partícula describe una trayectoria circular de radio l

${\displaystyle \begin{array}{l}m\frac{v^2}{l}=T-mg\cos \theta \\ T=m\frac{v^2}{l}+mg\cos \theta \end{array}}$

La tensión del hilo tiene que ser positiva T>0

• Movimiento en la dirección tangencial

ma_t=-mg·sinθ-λv²

La aceleración tangencial de la partícula es a_t=dv/dt.

La relación entre la aceleración tangencial a_t y la aceleración angular α es a_t=α·l=l·d²θ/dt². La ecuación del movimiento se escribe en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta +\gamma l{\left(\frac{d\theta }{dt}\right)}^2=0\{\begin{array}{l}\gamma >0\frac{d\theta }{dt}>0\\ \gamma <0\frac{d\theta }{dt}<0\end{array}}$

Solución numérica

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, el móvil parte en reposo dθ/dt=0 desde θ=θ₀

w0=100; %frecuencia angular rad/s
k=0.7; % gamma·l, constante de amortiguamiento
x0=pi/3; %ángulo inicial

f=@(t,x) [x(2);-k*x(2)^2*sign(x(2))-w0^2*sin(x(1))]; 
[t,x]=ode45(f,[0,1],[x0,0]);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Oscilador amortiguado')

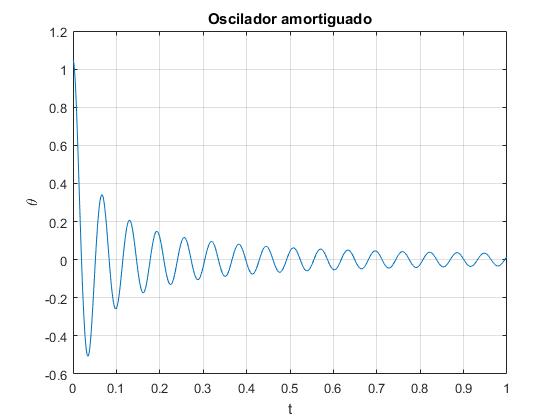
Un resultado similar al del oscilador lineal

La mayor riqueza de comportamientos se produce para la condición inicial siguiente: en la posición de partida θ₀, la velocidad de la partícula es v₀, que trataremos en el siguiente sección

Solución analítica

Transformamos la ecuación diferencial de segundo orden en θ y t en una de primer orden en v=l·dθ/dt y θ donde v es la velocidad de la partícula

${\displaystyle \begin{array}{l}\frac{1}{l}\frac{dv}{dt}+\frac{g}{l}\sin \theta +\gamma \frac{v^2}{l}=0\\ \frac{dv}{dt}=\frac{dv}{d\theta }\frac{d\theta }{dt}=\frac{v}{l}\frac{dv}{d\theta }=\frac{1}{2l}\frac{d{v}^2}{d\theta }\\ \frac{d{v}^2}{dt}+2\gamma l{v}^2=-2gl\sin \theta \end{array}}$

Llamando z=v², la solución particular es z₁=Asinθ+Bcosθ que introducimos en la ecuación diferencial para calcular los coeficientes A y B

${\displaystyle z_1=\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos \theta -2\gamma l\sin \theta \right)}$

La solución de la homogénea es z₂=C·exp(-2γlθ). La solución completa es v²=z₁+z₂

${\displaystyle v^2=C\exp \left(-2\gamma l\theta \right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos \theta -2\gamma l\sin \theta \right)}$

El coeficiente C se determina a partir de las condiciones iniciales: en la posición inicial θ₀, la partícula lleva una velocidad v₀.

${\displaystyle v_0^2=C\exp \left(-2\gamma l{\theta }_0\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)}$

La velocidad v de la partícula en la posición angular θ es

${\displaystyle v^2=v_0^2\exp \left(-2\gamma l(\theta -{\theta }_0)\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)\right\}}$

La tensión del hilo es

${\displaystyle \frac{T}{mg}=2\frac{v_0^2}{2gl}\exp \left(-2\gamma l(\theta -{\theta }_0)\right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)\right\}+\cos \theta }$

Si no hay rozamiento γ=0,

${\displaystyle v^2=v_0^2+2gl\left(\cos \theta -\cos {\theta }_0\right)}$

Ecuación que se obtiene aplicando el principio de conservación de la energía

El estudio de los distintos casos es similar al de la página titulada Rozamiento en el bucle

Posición angular final, θ<π/2

Cuando la posición angular final θ<π/2, es el caso más simple de analizar ya que la tensión del hilo T es siempre positiva

Calculamos la velocidad inicial v_0,π/2 que deberíamos impartir a la partícula en la posición inicial θ₀ para que llegue justamente a la posición θ=π/2, (con velocidad nula)

${\displaystyle \begin{array}{l}0=v_{\mathrm{0,}\pi /2}^2\exp \left(-2\gamma l\left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{-2\gamma l-\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l\left(\frac{\pi }{2}-{\theta }_0\right)\right)\right\}\\ v_{\mathrm{0,}\pi /2}^2=\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{2\gamma l\exp \left(\gamma l(\pi -2{\theta }_0)\right)+\cos {\theta }_0-2\gamma l\sin {\theta }_0\right\}\end{array}}$

Una expresión más simple se obtiene cuando la posición inicial θ₀=0, el péndulo parte del origen

${\displaystyle \frac{v_{\mathrm{0,}\pi /2}^2}{2gl}=\frac{1}{1+4{\gamma }^2{l}^2}\left\{2\gamma l\exp \left(\gamma l\pi \right)+1\right\}}$

Si la velocidad inicial v₀ es menor, entonces la posición final del péndulo θ₁<π/2, que vamos a calcular resolviendo la ecuación transcendente por procedimiento fzero de MATLAB

${\displaystyle \begin{array}{l}0=v_0^2\exp \left(-2\gamma l(\theta -{\theta }_0)\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)\right\}\\ \frac{v_0^2}{2gl}\left(1+4{\gamma }^2{l}^2\right)+\left(\cos \theta -2\gamma l\sin \theta \right)\exp \left(2\gamma l(\theta -{\theta }_0)\right)-\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)=0\end{array}}$

Supongamos que el péndulo parte del origen θ₀=0, con velocidad v₀ menor que la máxima v_{0, π/2}. Sea k=γl=0.25, la velocidad máxima v_0,π/2=1.2951 en unidades $\sqrt{2gl}$. Si el péndulo parte del origen con velocidad v₀=0.25, llega a la posición final θ₁=70.38°

k=0.25; %rozamiento
v_max=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para pi/2
disp(v_max)
v0=1; %velocidad inicial
f=@(x) v0^2*(1+4*k^2)+(cos(x)-2*k*sin(x))*exp(2*k*x)-1;
th_1=fzero(f, [0, pi/2]); %posición final
disp(th_1*180/pi)

    1.2951
   70.3839

Representamos la posición final θ₁ en función de la velocidad inicial $\frac{v_0}{\sqrt{2gl}}$, para varios valores de k=γl. La posición inicial θ₀=0 (el péndulo parte del origen)

hold on
for k=[0,0.05,0.1,0.25] %rozamiento
    v_max=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para pi/2
    vv=linspace(0,v_max,100); 
    th=zeros(1,length(vv));
    th(end)=pi/2;
    i=1;
    for v0=vv(1:end-1)
        f=@(x) v0^2*(1+4*k^2)+(cos(x)-2*k*sin(x))*exp(2*k*x)-1;
        th(i)=fzero(f, [0, pi/2]);
        i=i+1;
    end
    plot(vv,th, 'displayName',num2str(k)),
end
hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12','\pi/2'})
xlabel('v_0')
ylabel('\theta')
grid on
legend('-DynamicLegend','location','best')
title('Posición angular final')

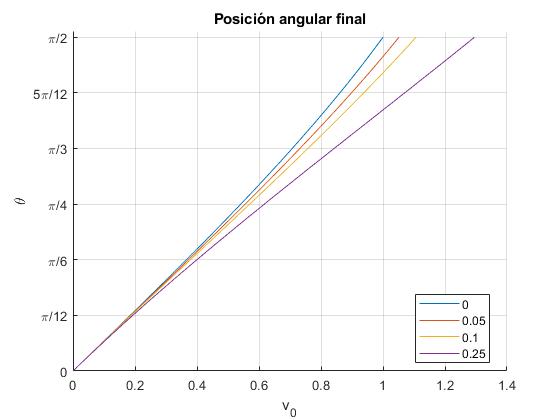
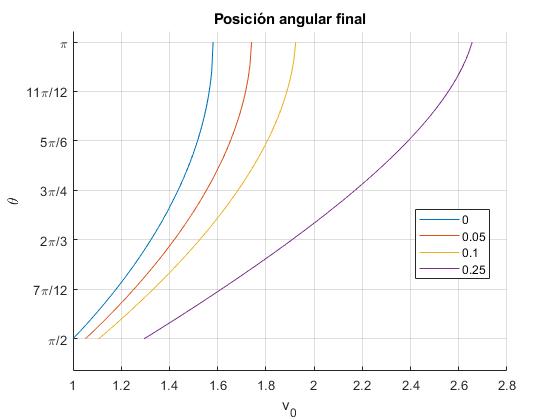
Posición angular final, π/2<θ<π

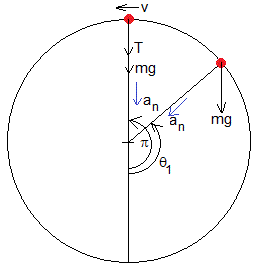
Para que la partícula pase por la posición más alta de su trayectoria θ=π, debe llevar una velocidad mínima. Aplicando la ecuación de la dinámica del movimiento circular

${\displaystyle m\frac{v^2}{l}=mg+T}$

La velocidad mínima, se obtiene cuando la tensión del hilo T es cero

${\displaystyle v=\sqrt{gl}}$

La velocidad inicial v_0,π que deberá llevar la partícula para que llegue a la posición final θ=π con esta velocidad mínima v²=gl es

${\displaystyle \begin{array}{l}gl=v_{\mathrm{0,}\pi }^2\exp \left(-2\gamma l(\pi -{\theta }_0)\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{-1-\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\pi -{\theta }_0)\right)\right\}\\ v_{\mathrm{0,}\pi }^2=\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos {\theta }_0-2\gamma l\sin {\theta }_0+\exp \left(2\gamma l(\pi -{\theta }_0)\right)\right\}+gl\exp \left(2\gamma l(\pi -{\theta }_0)\right)\end{array}}$

Si la velocidad inicial de la partícula es inferior a v_0,π pero superior a v_0,π/2, la posición angular final θ₁>π/2 pero θ₁<π. La posición final se obtiene cuando la tensión T del hilo se hace cero o bien, cuando la velocidad de la partícula vale (véase la figura)

${\displaystyle \begin{array}{l}m\frac{v^2}{l}=-mg\cos {\theta }_1\\ v^2=-gl\cos {\theta }_1\end{array}}$

A partir de esta posición, la partícula describe una trayectoria parabólica

La posición final θ₁ se calcula resolviendo la ecuación transcendente por el procedimiento fzero de MATLAB

${\displaystyle \begin{array}{l}\frac{v_0^2}{gl}\exp \left(-2\gamma l(\theta -{\theta }_0)\right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)\right\}+\cos \theta =0\\ \frac{v_0^2}{2gl}=\frac{1}{1+4{\gamma }^2{l}^2}\left\{\cos {\theta }_0-2\gamma l\sin {\theta }_0-\left(\cos \theta -2\gamma l\sin \theta \right)\exp \left(2\gamma l(\theta -{\theta }_0)\right)\right\}-\frac{1}{2}\cos \theta \exp \left(2\gamma l(\theta -{\theta }_0)\right)\end{array}}$

Supongamos que el péndulo parte del origen θ₀=0, con velocidad v₀ mayor que v_0,π/2 y menor que v_0,π. Sea k=γl=0.25, la velocidad mínima v_0,π/2=1.2951 y la máxima v_0,π=2.6559 en unidades $\sqrt{2gl}$. Si el péndulo parte del origen con velocidad v₀=1.8, llega a la posición final θ₁=114.31°

k=0.25; %rozamiento
v_min=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para pi/2
v_max=sqrt((1+exp(2*k*pi))/(1+4*k^2)+exp(2*k*pi)/2); %velocidad inicial para pi
disp([v_min,v_max])
v0=1.8;
f=@(x) (1-(cos(x)-2*k*sin(x))*exp(2*k*x))/(1+4*k^2)-exp(2*k*x)*cos(x)/2-v0^2;
th_1=fzero(f, [pi/2, pi]);
disp(th_1*180/pi) 

    1.2951    2.6559
  114.3149

Representamos la posición final θ₁ en función de la velocidad inicial $\frac{v_0}{\sqrt{2gl}}$, para varios valores de k=γl. La posición inicial θ₀=0 (el péndulo parte del origen)

hold on
for k=[0,0.05,0.1,0.25]
    v_min=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para  pi/2
    v_max=sqrt((1+exp(2*k*pi))/(1+4*k^2)+exp(2*k*pi)/2); %v. inicial para  pi
    vv=linspace(v_min,v_max,100); 
    th=zeros(1,length(vv));
    th(1)=pi/2;
    th(end)=pi;
    i=2;
    for v0=vv(2:end-1)
        f=@(x) (1-(cos(x)-2*k*sin(x))*exp(2*k*x))/(1+4*k^2)-exp(2*k*x)*cos(x)/2-
v0^2;
        th(i)=fzero(f, [pi/2, pi]);
        i=i+1;
    end
    plot(vv,th, 'displayName',num2str(k)),
end
hold off
set(gca,'YTick',pi/2:pi/12:pi)
set(gca,'YTickLabel',{'\pi/2','7\pi/12','2\pi/3','3\pi/4','5\pi/6', '11\pi/12',
'\pi'})
xlabel('v_0')
ylabel('\theta')
grid on
legend('-DynamicLegend','location','best')
title('Posición angular final')

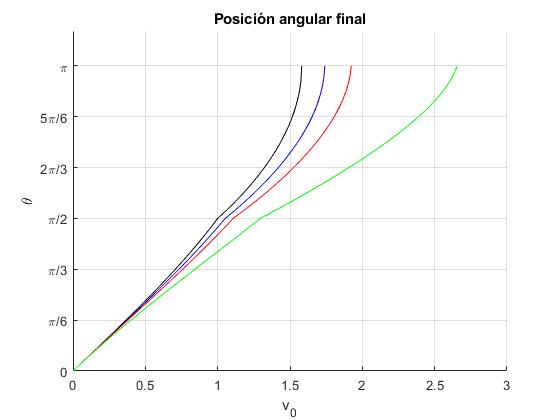
Unimos las dos porciones de código, para representar la posición final θ₁ en función de la velocidad inicial para varios valores del parámetro k: 0 (negro), 0.05 (azul), 0.1 (rojo), 0.25 (verde)

hold on
colores=['k','b','r','g'];
indice=1;
for k=[0,0.05,0.1,0.25]
    v_max=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para pi/2
    vv=linspace(0,v_max,100); 
    th=zeros(1,length(vv));
    th(end)=pi/2;
    i=1;
    for v0=vv(1:end-1)
        f=@(x) v0^2*(1+4*k^2)+(cos(x)-2*k*sin(x))*exp(2*k*x)-1;
        th(i)=fzero(f, [0, pi/2]);
        i=i+1;
    end
    plot(vv,th, colores(indice))

    v_min=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para  pi/2
    v_max=sqrt((1+exp(2*k*pi))/(1+4*k^2)+exp(2*k*pi)/2); %v. inicial para  pi
    vv=linspace(v_min,v_max,100); 
    th=zeros(1,length(vv));
    th(1)=pi/2;
    th(end)=pi;
    i=2;
    for v0=vv(2:end-1)
        f=@(x) (1-(cos(x)-2*k*sin(x))*exp(2*k*x))/(1+4*k^2)-exp(2*k*x)*cos(x)/2-
v0^2;
        th(i)=fzero(f, [pi/2, pi]);
        i=i+1;
    end
    plot(vv,th, colores(indice))
    indice=indice+1;
end
hold off
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('v_0')
ylabel('\theta')
grid on
title('Posición angular final')

Posición angular final, π<θ<2π

Si la velocidad inicial v₀ es mayor que v_0,π, la tensión del hilo T en la posición más elevada θ=π es positiva y el movimiento del péndulo se extiende más allá, hasta que la tensión T se anule en el intervalo π<θ<3π/2.

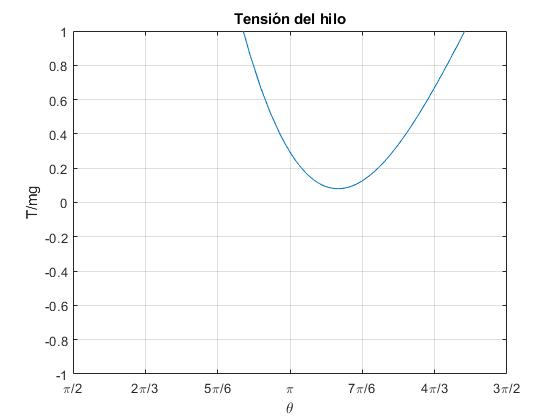
Por ejemplo, para k=0.5, v_0,π=4.8622. Representamos la tensión T/(mg) del hilo en función del ángulo θ en el intervalo (π, 3π/2) para una velocidad inicial un poco mayor, v₀=5.07

k=0.5; %rozamiento
v_max=sqrt((1+exp(2*k*pi))/(1+4*k^2)+exp(2*k*pi)/2); %velocidad inicial para pi
disp(v_max)
v0=5.07; %velocidad inicial
f=@(x) 2*v0^2*exp(-2*k*x)+2*(cos(x)-2*k*sin(x)-exp(-2*k*x))/(1+4*k^2)+cos(x);
hold on
fplot(f, [pi/2,3*pi/2])
line([2*pi/3,3*pi/2],[0,0],'color','k')
plot(198*pi/180,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
line([198*pi/180,198*pi/180],[-1,0],'color','k','lineStyle','--')
hold off
set(gca,'XTick',pi/2:pi/6:3*pi/2)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi','7\pi/6', '4\pi/3','3\pi/2'})
xlabel('\theta')
ylabel('T/mg')
grid on
ylim([-1,1])
title('Tensión del hilo')

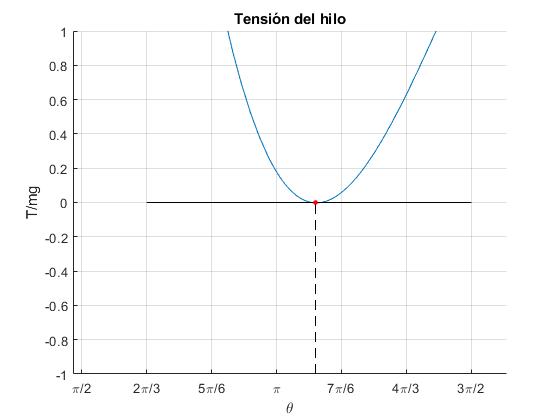
4.8622

Observamos que la tensión del hilo es positiva, toma un valor próximo a cero para un ángulo cercano a θ_c=198°. Para este ángulo crítico, la tensión T y su derivada dT/dθ (pendiente de la recta tangente) se anulan simultáneamente, tal como apreciamos en la figura. El péndulo continuará su movimiento hasta alcanzar el punto más bajo de su trayectoria θ=2π

Para hacer los cálculos más sencillos, supongamos que partimos del origen θ₀=0. La tensión del hilo es

${\displaystyle \frac{T}{mg}=2\frac{v_0^2}{2gl}\exp \left(-2\gamma l\theta \right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\exp \left(-2\gamma l\theta \right)\right\}+\cos \theta }$

Su derivada es

${\displaystyle \frac{1}{mg}\left(\frac{dT}{d\theta }\right)=2\frac{v_0^2}{2gl}\left(-2\gamma l\right)\exp \left(-2\gamma l\theta \right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{-\sin \theta -2\gamma l\cos \theta +2\gamma l\exp \left(-2\gamma l\theta \right)\right\}-\sin \theta }$

Resolvemos el sistema de dos ecuaciones con dos incógnitas, el ángulo crítico θ_c y la velocidad inicial crítica v_0,2π

${\displaystyle \{\begin{array}{l}2\frac{v_0^2}{2gl}\exp \left(-2\gamma l\theta \right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\exp \left(-2\gamma l\theta \right)\right\}+\cos \theta =0\\ 2\frac{v_0^2}{2gl}\left(-2\gamma l\right)\exp \left(-2\gamma l\theta \right)+\frac{2}{1+4{\gamma }^2{l}^2}\left\{-\sin \theta -2\gamma l\cos \theta +2\gamma l\exp \left(-2\gamma l\theta \right)\right\}-\sin \theta =0\end{array}}$

Eliminamos v₀ y llegamos a la ecuación

${\displaystyle \tan {\theta }_c=\frac{2}{3}k}$

que es un ángulo del tercer cuadrante. Una vez calculado este ángulo θ_c despejamos la velocidad inicial crítica, v_0,2π, tomando la primera del sistema de dos ecuaciones

${\displaystyle \frac{v_{\mathrm{0,2}\pi }^2}{2gl}=\frac{1}{1+4{\gamma }^2{l}^2}\left\{1-\left(\cos {\theta }_c-2\gamma l\sin {\theta }_c\right)\exp \left(2\gamma l{\theta }_c\right)\right\}-\frac{1}{2}\cos {\theta }_c\exp \left(2\gamma l{\theta }_c\right)}$

>> k=0.5;
>> th_c=pi+atan(2*k/3) %ángulo del tercer cuadrante
th_c =    3.4633

>> v_c=sqrt(((2*k*sin(th_c)-cos(th_c))*exp(2*k*th_c)+1)/(1+4*k^2)-
exp(2*k*th_c)*cos(th_c)/2)
v_c =    5.0732 %velocidad inicial crítica

>> f(3.4633) %tensión del hilo
ans =  -2.5339e-05

• Una velocidad inicial v₀ menor que la crítica v_0,2π, pero mayor que v_0,π

Implica que la tensión se hará cero para un determinado ángulo π<θ<θ_c, por ejemplo, para v₀=5.

k=0.5; %rozamiento
v_max=sqrt((1+exp(2*k*pi))/(1+4*k^2)+exp(2*k*pi)/2); %velocidad inicial para pi
disp(v_max)
v0=5; %velocidad inicial
f=@(x) 2*v0^2*exp(-2*k*x)+2*(cos(x)-2*k*sin(x)-exp(-2*k*x))/(1+4*k^2)+cos(x);
fplot(f, [pi/2,3*pi/2])
set(gca,'XTick',pi/2:pi/6:3*pi/2)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi','7\pi/6', '4\pi/3',
'3\pi/2'})
xlabel('\theta')
ylabel('T/mg')
grid on
ylim([-1,1])
title('Tensión del hilo')



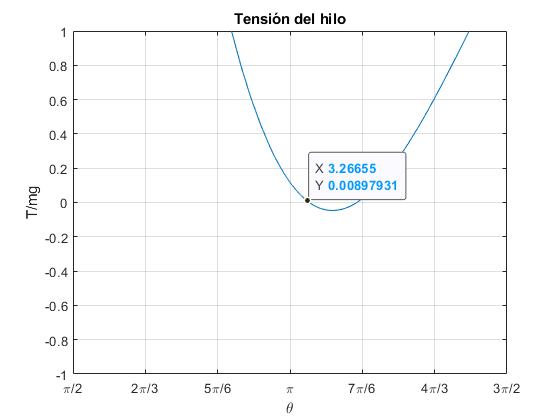
>> fzero(f,[pi,3.4633])
ans =    3.2815

• Una velocidad inicial mayor que la crítica v_0,2π

Implica que la tensión se mantendrá positiva y el péndulo llegará al punto más bajo de su trayectoria θ=2π, iniciándose un nuevo ciclo, por ejemplo, para v₀=5.2. Para obtener esta representación gráfica, en el script cambiamos el valor de la velocidad inicial

Posición angular final, θ≥2π

Cuando la velocidad inicial en el origen θ₀=0, es v₀≥v_0,2π el péndulo completa una vuelta θ=2π y regresa a la posición de partida. La nueva velocidad inicial de la partícula es

${\displaystyle v^2=v_0^2\exp \left(-2\gamma l·2\pi \right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{1-\exp \left(-2\gamma l·2\pi \right)\right\}}$

Con esta velocidad inicial, hay que volver a analizar el movimiento del péndulo para el valor dado de k=γ·l

Oscilaciones amortiguadas

El caso más importante se produce cuando la posición final θ₁<π/2. El primero tratado en esta página.

1. El péndulo se mueve en el sentido contrario a las agujas del reloj, v>0.

Como ya se ha analizado, la ecuación diferencial que describe el movimiento desde θ₀ con velocidad v₀ hasta θ₁ en reposo es

${\displaystyle \frac{d{v}^2}{dt}+2\gamma l{v}^2=-2gl\sin \theta }$

La solución, con la condición inicial: en la posición θ₀ la velocidad inicial es v₀

${\displaystyle v^2=v_0^2\exp \left(-2\gamma l(\theta -{\theta }_0)\right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)\right\}}$

El péndulo se detiene para el ángulo θ₁, solución de la ecuación transcendente

${\displaystyle \frac{v_0^2}{2gl}+\frac{1}{1+4{\gamma }^2{l}^2}\left\{\left(\cos \theta -2\gamma l\sin \theta \right)\exp \left(-2\gamma l(\theta -{\theta }_0)\right)-\left(\cos {\theta }_0-2\gamma l\sin {\theta }_0\right)\right\}=0}$

2. El péndulo se mueve en el sentido de las agujas del reloj, v<0.

Cuando el péndulo inicial el camino de vuelta, la velocidad cambia de signo v<0 y la fuerza de rozamiento también, la ecuación del movimiento es

${\displaystyle \frac{d{v}^2}{dt}-2\gamma l{v}^2=-2gl\sin \theta }$

Llamando z=v², la solución particular es z₁=Asinθ+Bcosθ que introducimos en la ecuación diferencial para calcular los coeficientes A y B

${\displaystyle z_1=\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos \theta +2\gamma l\sin \theta \right)}$

La solución de la homogénea es z₂=C·exp(2γlθ). La solución completa es v²=z₁+z₂

${\displaystyle v^2=C\exp \left(2\gamma l\theta \right)+\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos \theta +2\gamma l\sin \theta \right)}$

Es la misma solución deducida anteriormente, sustituyendo γ por -γ

El coeficiente C se determina a partir de las condiciones iniciales: en la posición inicial θ₁, el móvil parte del reposo.

${\displaystyle \begin{array}{l}C=-\frac{2gl}{1+4{\gamma }^2{l}^2}\left(\cos {\theta }_1+2\gamma l\sin {\theta }_1\right)\exp \left(-2\gamma l{\theta }_1\right)\\ v^2=\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos \theta +2\gamma l\sin \theta -\left(\cos {\theta }_1+2\gamma l\sin {\theta }_1\right)\exp \left(2\gamma l(\theta -{\theta }_1)\right)\right\}\end{array}}$

El péndulo se detiene para el ángulo θ₂, solución de la ecuación transcendente

${\displaystyle \cos \theta +2\gamma l\sin \theta -\left(\cos {\theta }_1+2\gamma l\sin {\theta }_1\right)\exp \left(2\gamma l(\theta -{\theta }_1)\right)=0}$

3. El péndulo se mueve en el sentido contrario a las agujas del reloj, v>0.

El péndulo parte en reposo desde la posición θ₂, su velocidad es v>0,

${\displaystyle v^2=\frac{2gl}{1+4{\gamma }^2{l}^2}\left\{\cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_2-2\gamma l\sin {\theta }_2\right)\exp \left(-2\gamma l(\theta -{\theta }_2)\right)\right\}}$

El péndulo se detiene para el ángulo θ₃, solución de la ecuación transcendente

${\displaystyle \cos \theta -2\gamma l\sin \theta -\left(\cos {\theta }_2-2\gamma l\sin {\theta }_2\right)\exp \left(-2\gamma l(\theta -{\theta }_2)\right)=0}$

4. El péndulo se mueve en el sentido de las agujas del reloj, v<0.

y así, sucesivamente

Representamos el movimiento del péndulo en el espacio de las fases para k=0.5. El péndulo parte del origen θ₀=0, con velocidad inicial v₀<v_0,π/2=1.2951

k=0.25; %rozamiento
v_max=sqrt((1+2*k*exp(k*pi))/(1+4*k^2)); %velocidad inicial para pi/2
disp(v_max)
v0=1.2; %velocidad inicial
f=@(x)  v0^2*(1+4*k^2)+(cos(x)-2*k*sin(x))*exp(2*k*x)-1;
th_1=fzero(f,[0,pi/2]); %posición angular final
th=linspace(0,th_1,100);
xx=th(2:end-1);
v=@(x) sqrt(v0^2*exp(-2*k*x)+(cos(x)-2*k*sin(x)-exp(-2*k*x))/(1+4*k^2));
y=[v0,v(xx),0]; 
hold on
plot(th,y);
for i=1:10
    f=@(x) cos(x)+2*k*sin(x)-(cos(th_1)+2*k*sin(th_1))*exp(2*k*(x-th_1));
    th_2=fzero(f,[0,-th_1]);
    th=linspace(th_2,th_1,100);
    xx=th(2:end-1);
    %los puntos de retorno x(1) y x(end) tienen velocidad cero
    v=@(x) sqrt((cos(x)+2*k*sin(x)-(cos(th_1)+2*k*sin(th_1))*
exp(2*k*(x-th_1)))/(1+4*k^2));
    y=[0,v(xx),0]; 
    plot(th,-sign(k)*y);
    th_1=th_2;
    k=-k;
end
hold off
grid on
set(gca,'XTick',-pi/2:pi/6:pi/2)
set(gca,'XTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0','\pi/6', '\pi/3','\pi/2'})
xlabel('\theta')
ylabel('v')
title('Espacio de las fases')

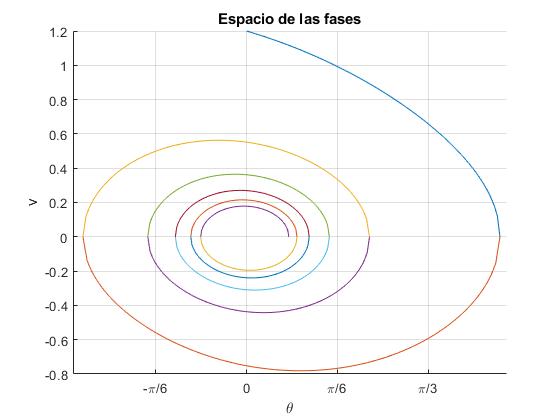
1.2951

Actividades

Se introduce

• El coeficiente de rozamiento, k en el control titulado Coeficiente
• La velocidad inicial v₀, en unidades $\sqrt{2gl}$ en el control titulado Velocidad inicial
• Se ha fijado la longitud del péndulo l=1

Se pulsa el botón titulado Nuevo y se observa el movimiento del péngulo

En la parte izquierda, se proporcionanlos datos del tiempo t, la posición angular θ, en grados, la velocidad angular ω=dθ/dt, y la tensión del hilo T

Cuando la velocidad v es cero, el cuerpo se detiene. Cuando la tensión del hilo T es nula, el cuerpo describe una trayectoria parabólica.

En la parte derecha, se representa el balance energético: la energía cinética (en color rojo), la energía potencial (en color azul) y el trabajo de la fuerza de rozamiento (en color negro)

Referencias

Marko V Lubarda, Vlado A Lubarda. An analysis of pendulum motion in the presence of quadratic and linear drag. Eur. J. Phys. 42 (2021) 055014