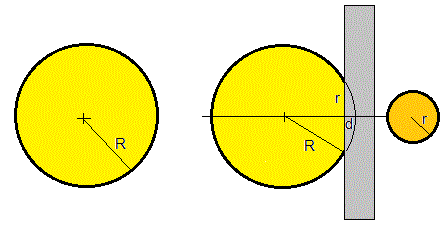
Cuando una pelota de radio R que está inflada con una presión ΔP choca con una pared rígida la pelota se deforma. En una primera aproximación, imaginamos la esfera deformada una longitud d, por lo que el área de contacto es un círculo de radio r.

${\displaystyle R^2=r^2+{(R-d)}^2}$

Calculamos el volumen de un casquete esférico comprendido entre x=R-d y x=R. Para ello, dividimos la esfera cuyo volumen es V=4πR³/3 en porciones diferenciales de radio y y anchura dx, tal como se muestra en la figura

${\displaystyle \Delta V={\displaystyle \underset{R-d}{\overset{R}{\int }}\pi y^{2}dx}={\displaystyle \underset{R-d}{\overset{R}{\int }}\pi (R^2-x^2)dx}=\pi \left(R{d}^2-\frac{d^3}{3}\right)}$

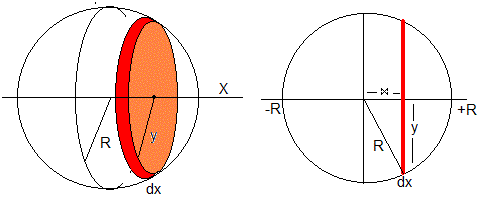
El cociente ΔV/V es pequeño si la deformación d es pequeña y por tanto, podemos considerar que la sobrepresión ΔP en el interior de la pelota no cambia apreciablemente durante la deformación.

La fuerza que ejerce la pared sobre la pelota, es el producto de la sobrepresión ΔP por el área de contacto

${\displaystyle F=\Delta P·\pi r^2=\Delta P·\pi \left(R^2-{(R-d)}^2\right)\approx 2\pi R·\Delta P·d}$

La fuerza F es proporcional a la deformación d.

Para dar cuenta de la pérdida de energía durante el choque de la pelota con la pared rígida, supondremos que además está presente una fuerza de rozamiento proporcional a la velocidad λv. El resultado es la ecuación del movimiento de un oscilador amortiguado de masa m y constante k=2πRΔP

La ecuación diferencial del movimiento del c.m. de la pelota es

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0{\omega }_0^2=\frac{2\pi R·\Delta P}{m}}$

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}x=\left(A\sin (\omega t)+B\cos (\omega t)\right)\exp (-\gamma t){\omega }^2={\omega }_0^2-{\gamma }^2\\ v=\frac{dx}{dt}=\omega \left(A\cos (\omega t)-B\sin (\omega t)\right)\exp (-\gamma t)-\gamma \left(A\sin (\omega t)+B\cos (\omega t)\right)\exp (-\gamma t)\end{array}}$

Las condiciones iniciales son, en el instante t=0, x=0 y dx/dt=v₀. Donde v₀ es la velocidad del c.m. de la pelota justamente antes de su choque con la pared rígida.

${\displaystyle \begin{array}{l}B=0\\ v_0=\omega A-\gamma B\end{array}\}A=\frac{v_0}{\omega }}$

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}x=\frac{v_0}{\omega }\exp \left(-\gamma t\right)\sin \left(\omega t\right)\\ \frac{dx}{dt}=\frac{v_0}{\omega }\exp \left(-\gamma t\right)\left(-\gamma \sin \left(\omega t\right)+\omega \cos \left(\omega t\right)\right)\end{array}}$

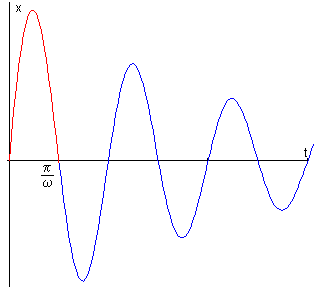
La pelota está en contacto con la pared un tiempo t_c

${\displaystyle t_c=\frac{\pi }{\omega }=\frac{\pi }{\sqrt{\frac{2\pi R·\Delta P}{m}-{\gamma }^2}}\approx \sqrt{\frac{\pi m}{2R·\Delta P}}}$

Para γ<<ω₀, ω≈ω₀

La figura nos muestra la representación gráfica de la posición del c.m. del balón x en función del tiempo t. Después de haber completado un semiperiodo de oscilación P/2=π/ω, (línea de color rojo) el c.m. del balón se aleja de la pared con una velocidad v dada por

${\displaystyle v=-v_0\exp \left(-\pi \frac{\gamma }{\omega }\right)}$

Se define el coeficiente de restitución e como el cociente entre la velocidad final v tras el choque entre la velocidad inicial v₀ justamente antes del choque con la pared.

${\displaystyle e=\exp \left(-\pi \frac{\gamma }{\omega }\right)}$

El coeficiente de restitución depende de dos parámetros que describen nuestro modelo simplificado, la frecuencia de la oscilación amortiguada y la constante de amortiguamiento.

Si la constante de amortiguamiento es cero, γ=0, no hay rozamiento interno entre las diversas partes del balón, no hay pérdidas de energía, el choque es perfectamente elástico, y e=1.

Energías

La energía perdida en el choque es la diferencia entre la energía cinética final e inicial

${\displaystyle \Delta E=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2=-\frac{1}{2}m{v}_0^2\left(1-\exp \left(-2\pi \frac{\gamma }{\omega }\right)\right)}$

Que es igual al trabajo de la fuerza de rozamiento λv durante el tiempo t_c de choque

${\displaystyle \Delta E={\displaystyle \underset{0}{\overset{t_c}{\int }}-\lambda v·(vdt)=}-2m\gamma {\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}{v}^{2}dt}}$

Utilizamos MATLAB para hacer la integral

>> syms v0 w gamma m t;
>> v=v0*exp(-gamma*t)*(-gamma*sin(w*t)+w*cos(w*t))/w;
>> -2*m*gamma*int(v^2,t,0,pi/w)
ans =(m*v0^2*(exp(-(2*pi*gamma)/w) - 1))/2

Actividades

Fijaremos la frecuencia propia ω₀ en el valor 100, permitiéndonos variar, la constante de amortiguamiento γ en el intervalo de 0 (choques elásticos) a 20.

Se introduce

• la constante de amortiguamiento en el control titulado Constante γ.
• la velocidad inicial en el control titulado Velocidad.

Se pulsa el botón titulado Nuevo

Referencias

Charles de Izarra. Duration of an elastic collision. Eur. J. Phys. 33 (2012) 997-1006

Ajay Wadhwa. Study of the dynamic properties and effects of temperature using a spring model for the bouncing ball. Eur. J. Phys. 34 (2013) 703-713