Masa unida a un muelle elástico

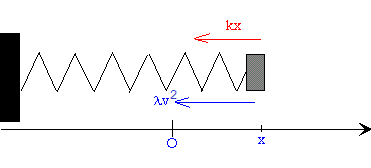
Las fuerzas que actúan sobre el móvil son: la fuerza elástica F=-kx, y la fuerza de rozamiento de sentido contrario a la velocidad F_r=-λv², donde λ es una constante que depende del sistema físico particular.

Dado que v² es positivo, λ será positiva si v>0 y negativa si v<0

La ecuación del movimiento se escribe

ma=-kx-λv²

Expresamos la ecuación del movimiento en forma de ecuación diferencial, teniendo en cuenta que la aceleración es la derivada segunda de la posición x, y la velocidad es la derivada primera de x.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+\gamma {\left(\frac{dx}{dt}\right)}^2+{\omega }_0^{2}x=0\{\begin{array}{l}\gamma >0\frac{dx}{dt}>0\\ \gamma <0\frac{dx}{dt}<0\end{array}\\ {\omega }_0^2=\frac{k}{m}\gamma =\frac{\lambda }{m}\end{array}}$

• ω₀ es la frecuencia natural o propia del oscilador
• γ es la constante de amortiguamiento

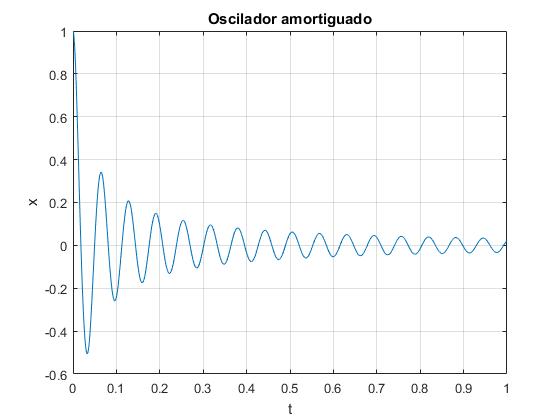
Solucción numérica

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, el móvil parte en reposo dx/dt=0 desde x=x₀

w0=100; %frecuencia angular rad/s
g=0.7; %constante en 1/m
x0=1; %posición inicial
f=@(t,x) [x(2);-g*x(2)^2*sign(x(2))-w0*w0*x(1)]; 
[t,x]=ode45(f,[0,1],[x0,0]);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

Solución analítica

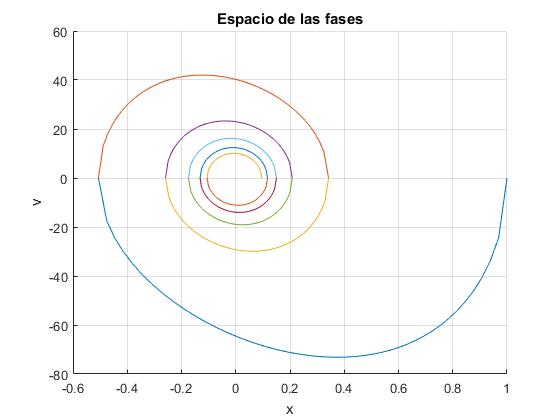
El espacio de las fases nos muestra otra perspectiva del comportamiento del oscilador. Se representa el momento lineal (o la velocidad) v en el eje vertical y la posición del móvil x en el eje horizontal.

Transformamos la ecuación diferencial de segundo orden en x y t en una de primer orden en v y x

${\displaystyle \begin{array}{l}\frac{dv}{dt}+\gamma v^2+{\omega }_0^{2}x=0\{\begin{array}{l}\gamma >0v>0\\ \gamma <0v<0\end{array}\\ v\frac{dv}{dx}+\gamma v^2+{\omega }_0^{2}x=0\\ \frac{1}{2}\frac{dz}{dx}+\gamma z=-{\omega }_0^{2}xz=v^2\end{array}}$

La solución particular es z₁=Ax+B que introducimos en la ecuación diferencial para calcular los coeficientes A y B

${\displaystyle z_1=\frac{{\omega }_0^2}{\gamma }\left(\frac{1}{2\gamma }-x\right)}$

La solución de la homogénea es z₂=C·exp(-2γx). La solución completa es z=z₁+z₂

${\displaystyle z=C{e}^{-2\gamma x}-\frac{{\omega }_0^2}{\gamma }x+\frac{{\omega }_0^2}{2{\gamma }^2}}$

El coeficiente C se determina a partir de las condiciones iniciales: en la posición inicial x₀, el móvil parte del reposo, v=0

${\displaystyle v^2=\frac{{\omega }_0^2}{\gamma }\left\{\left(x_0-\frac{1}{2\gamma }\right)e^{-2\gamma (x-x_0)}-\left(x-\frac{1}{2\gamma }\right)\right\}}$

Vamos a representar la velocidad v en función de la posición x del móvil

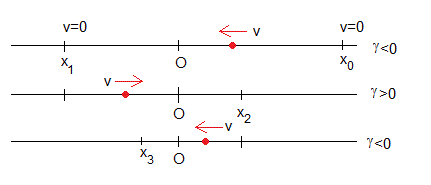
Primera etapa

Partimos de x₀>0 con velocidad inicial v=0, la partícula se mueve hacia la izquierda v<0 (γ<0) hasta que se detiene en x₁. Esta posición es la raíz de la ecuación transcendente

${\displaystyle \left(x_0-\frac{1}{2\gamma }\right)e^{-2\gamma (x-x_0)}-\left(x-\frac{1}{2\gamma }\right)=0}$

Una vez calculado x₁ se representa la función v(x) en el intervalo (x₁, x₀)

${\displaystyle v=\mathrm{sgn}(\gamma )·{\omega }_0\sqrt{\frac{1}{\gamma }\left\{\left(x_0-\frac{1}{2\gamma }\right)e^{-2\gamma (x-x_0)}-\left(x-\frac{1}{2\gamma }\right)\right\}}}$

donde la función sgn(γ) indica que si γ<0 entonces v<0

Segunda etapa

Ahora x₁ es la posición de partida y la partícula, se mueve hacia la derecha v>0 y por tanto, γ>0. La posición x₂ se calcula resolviendo la ecuación transcendente con γ cambiado de signo

Una vez calculado x₂ se representa la función v(x) en el intervalo (x₁, x₂), donde la función sgn(γ) indica que si γ>0 entonces v>0

Se ha completado el primer periodo, se repite las dos etapas para los siguientes. El código MATLAB que calcula 10 semiperiodos es el siguiente

w0=100; %frecuencia angular rad/s
g=0.7; %constante de amortiguamiento
x0=1; %posición inicial

hold on
for i=1:10
    g=-g;
    f=@(x) (x0-1/(2*g))*exp(-2*g*(x-x0))-(x-1/(2*g));
    x1=fzero(f,-x0);
    x=linspace(x1,x0,50);
    xx=x(2:end-1);
    %los puntos de retorno x(1) y x(end) tienen velocidad cero
    y=[0,w0*sqrt(f(xx)/g),0]; 
    plot(x,sign(g)*y);
    x0=x1;   
end
hold off
grid on
xlabel('x')
ylabel('v')
title('Espacio de las fases')

Dispositivo experimental

El dispositivo experimental es un péndulo formado por una varilla de masa m y longitud L unida a un disco de masa M y radio R, perpendicular a la dirección de la velocidad, tal como se muestra en la figura.

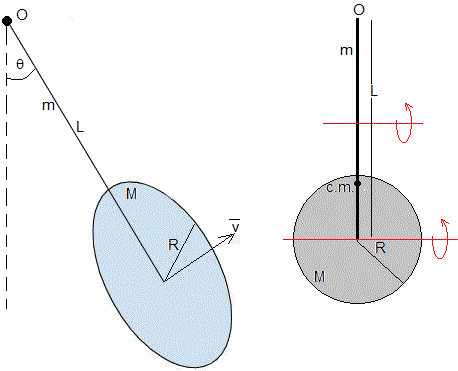
El momento de inercia respecto de un eje perpendicular al plano de oscilación y que pasa por O es la suma de los momentos de inercia

• de la varilla respecto a un eje perpendicular que pasa por uno de sus extremos
• de un disco respecto de un eje paralelo distante L del eje contenido en el plano del disco y que pasa por su centro

Aplicando el teorema de Steiner

${\displaystyle I=\left(\frac{1}{12}m{L}^2+m{\left(\frac{L}{2}\right)}^2\right)+\left(\frac{1}{4}M{R}^2+M{L}^2\right)=\frac{1}{3}m{L}^2+\frac{1}{4}M{R}^2+M{L}^2}$

La posición del dentro de masas, su distancia al centro O es

${\displaystyle h=\frac{m\frac{L}{2}+ML}{m+M}}$

Las fuerzas sobre el péndulo son

• El peso (m+M)g que actúa en el centro de masas

• Una fuerza de rozamiento proporcional al cuadrado de la velocidad en el centro del disco. Despreciaremos la fuerza de rozamiento sobre la varilla que supondremos delgada

${\displaystyle F_r=C_D\frac{1}{2}{\rho }_{f}A{v}^2}$

• La densida del fluido, aire, ρ_f=1.21 kg/m³
• Coeficiente de arrastre, C_D=1.2 para un disco
• Area del disco, A=πR²
• La velocidad del centro del disco es v=ωL

La variación de energía (cinética más potencial) entre los instantes t y t+dt, el péndulo se desplaza dθ y su cambio de velocidad es dω, es igual al trabajo de la fuerza de rozamiento entre dichos instantes -M_r·dθ.

• El momento de M_r respecto del centro O es M_r=F_rL, el trabajo de la fuerza de rozamiento en el movimiento de rotación es

${\displaystyle -M_{r}d\theta =-F_{r}L·d\theta }$

La fuerza de rozamiento es de sentido contrario al vector velocidad

• El cambio de energía cinética es

${\displaystyle d{E}_k=d\left(\frac{1}{2}I{\omega }^2\right)=\frac{1}{2}Id{\omega }^2}$

• El cambio de energía potencial es

Cuando el péndulo se ha desplazado θ de la posición de equelibrio estable, su energía potencial referida al centro O, es

${\displaystyle \begin{array}{l}{E}_p=-\left(m+M\right)gh\cos \theta \\ d{E}_p=\left(m+M\right)gh\sin \theta ·d\theta \end{array}}$

La relación entre estas tres magnitudes es

${\displaystyle \begin{array}{l}-F_{r}L·d\theta =d{E}_k+d{E}_p\\ -\frac{1}{2}{C}_D{\rho }_f\pi R^2{\left(\omega L\right)}^{2}L·d\theta =\frac{1}{2}Id{\omega }^2+\left(m+M\right)gh\sin \theta ·d\theta \end{array}}$

Dividiendo por I/2, llamando z=ω² y definiendo los parámetros a y b del siguiente modo

${\displaystyle \begin{array}{l}b=\frac{C_D{\rho }_f\pi R^2{L}^3}{\frac{1}{3}m{L}^2+\frac{1}{4}M{R}^2+M{L}^2}=\frac{C_D{\rho }_f\pi R^{2}L}{\frac{1}{3}m+\frac{1}{4}M\frac{R^2}{L^2}+M}\\ a=\frac{2\left(m+M\right)gh}{\frac{1}{3}m{L}^2+\frac{1}{4}M{R}^2+M{L}^2}=\frac{m+2M}{\frac{1}{3}m+\frac{1}{4}M\frac{R^2}{L^2}+M}\frac{g}{L}\end{array}}$

Obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}-bz·d\theta =dz+a\sin \theta ·d\theta \\ \frac{dz}{d\theta }+bz=-a\sin \theta \end{array}}$

Teniendo en cuenta que

${\displaystyle e^{-b\theta }\frac{d}{d\theta }\left(z{e}^{b\theta }\right)=bz+\frac{dz}{d\theta }}$

La ecuación diferencial se integra fácilmente, suponiendo que el péndulo se suelta ω=0, z=0 en el instante t=0, desde la posición θ₀

${\displaystyle \begin{array}{l}{e}^{-b\theta }\frac{d}{d\theta }\left(z{e}^{b\theta }\right)=-a\sin \theta \\ \frac{d}{d\theta }\left(z{e}^{b\theta }\right)=-a{e}^{b\theta }\sin \theta \\ {\omega }^2{e}^{b\theta }=-a{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{e}^{b\theta }\sin \theta }\end{array}}$

Integrando por partes dos veces

${\displaystyle \begin{array}{l}{\displaystyle \int e^{b\theta }\sin \theta ·d\theta },\{\begin{array}{l}u=e^{b\theta },du=b{e}^{b\theta }·d\theta \\ dv=\sin \theta ·d\theta ,v=-\cos \theta \end{array}\\ =-e^{b\theta }\cos \theta +b{\displaystyle \int e^{b\theta }\cos \theta ·d\theta },\{\begin{array}{l}u=e^{b\theta },du=b{e}^{b\theta }·d\theta \\ dv=\cos \theta ·d\theta ,v=\sin \theta \end{array}\\ =-e^{b\theta }\cos \theta +b\left\{e^{b\theta }\sin \theta -b{\displaystyle \int e^{b\theta }\sin \theta ·d\theta }\right\}\\ {\displaystyle \int e^{b\theta }\sin \theta ·d\theta }=\frac{e^{b\theta }\left(b\sin \theta -\cos \theta \right)}{1+b^2}\end{array}}$

El cuadrado de la velocidad angular vale

${\displaystyle \begin{array}{l}{\omega }^2{e}^{b\theta }={a\frac{e^{b\theta }\left(\cos \theta -b\sin \theta \right)}{1+b^2}|}_{{\theta }_0}^{\theta }\\ {\omega }^2=\frac{a}{1+b^2}\left\{\cos \theta -b\sin \theta -e^{b\left({\theta }_0-\theta \right)}\left(\cos {\theta }_0-b\sin {\theta }_0\right)\right\}\end{array}}$

La posición de retorno ω=0, es la raíz θ₁ de la ecuación trascendente

${\displaystyle \cos \theta -b\sin \theta -e^{b\left({\theta }_0-\theta \right)}\left(\cos {\theta }_0-b\sin {\theta }_0\right)=0}$

Al cambiar el signo de la velocidad angular ω después de cada posición de retorno ω=0, debe cambiar el signo del parámetro b, con el fin de asegurar que la fuerza de rozamiento es de sentido opuesto a la velocidad

Ejemplo

• longitud de la varilla, L=38 cm
• masa de la varilla, m=12.8 g
• radio del disco, R=6 cm
• masa del disco, M=15.2 g

Con estos datos obtenemos: a=56.9543, b=0.3190 s^-2

Sea la posición inicial θ₀=-π/2 (90°) en el instante t=0

1. Se calcula la posición final de retorno θ₁=1.1334 (65°), resolviendo la ecuación trascendente

${\displaystyle \cos \theta -b\sin \theta -e^{b\left({\theta }_0-\theta \right)}\left(\cos {\theta }_0-b\sin {\theta }_0\right)=0}$

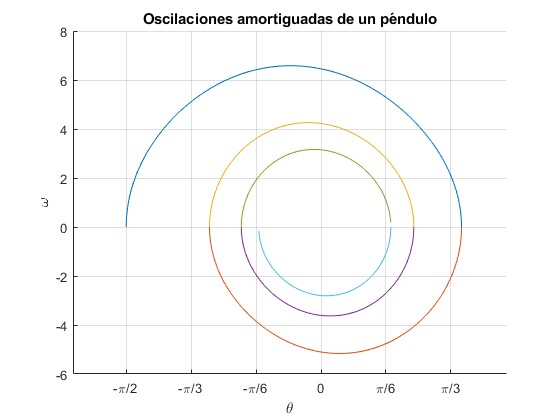
2. Se representa la función ω=ω(θ) desde θ₀=-π/2 (90°) a θ₁=1.1334 (65°)

${\displaystyle \omega =\sqrt{\frac{a}{1+b^2}\left\{\cos \theta -b\sin \theta -e^{b\left({\theta }_0-\theta \right)}\left(\cos {\theta }_0-b\sin {\theta }_0\right)\right\}}}$

3. Se cambia el signo de b

4. θ₀=1.1334 (65°) es la nueva posición inicial

5. Se calcula la posición final de retorno θ₁=-0.8991 (-51.5°) resolviendo la ecuación trascendente

6. Se representa la función ω=-ω(θ) desde θ₀=1.1334 (65°) a θ₁=-0.8991 (-51.5°)

7. Se cambia el signo de b

8. θ₀=-0.8991 (-51.5°) es la nueva posición inicial

Se repiten los ocho pasos...

L=38/100; %longitud varilla
m=12.8/1000; %masa varilla
R=6/100; %radio disco
M=15.2/1000; %masa disco
c_d=1.2; %coeficiente de forma
A=pi*R^2; %área del disco
rho=1.21; %densidad del aire

b=c_d*rho*A*L/(m/3+M*(R/L)^2/4+M); %parámetros
a=(m+2*M)*(9.8/L)/(m/3+M*(R/L)^2/4+M);
th_0=-pi/2; %posición de partida
hold on
for k=1:3
    f=@(x) cos(x)-b*sin(x)-(cos(th_0)-b*sin(th_0))*exp(b*(th_0-x));
    th_1=fzero(f,[0,pi/2]);
    disp(th_1*180/pi)
    g=@(x) sqrt(a*f(x)/(1+b^2));
    fplot(g,[th_0,th_1])
    th_0=th_1;
    b=-b;
    f=@(x) cos(x)-b*sin(x)-(cos(th_0)-b*sin(th_0))*exp(b*(th_0-x));
    th_1=fzero(f,[0,-pi/2]);
    disp(th_1*180/pi)
    g=@(x) -sqrt(a*f(x)/(1+b^2));
   fplot(g,[th_1,th_0])
   th_0=th_1;
   b=-b;
end
hold off
set(gca,'XTick',-pi/2:pi/6:pi/2)
set(gca,'XTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0','\pi/6', '\pi/3','\pi/2'})
grid on
xlabel('\theta')
ylabel('\omega')
title('Oscilaciones amortiguadas de un péndulo')

Referencias

Carl E Mungan, Trevor C Lipscombe. Oscillations of a quadratically damped pendulum. Eur. J. Phys. 34 (2013) pp. 1243–1253