En el péndulo giratorio de Pohl, la fuerza de rozamiento proporcional a la velocidad se origina por la acción del campo magnético producido por dos bobinas sobre las corrientes inducidas en el anillo de cobre. En el oscilador de PASCO es el campo magnético producido por un potente imán permente sobre las corrientes inducidas en un disco de aluminio, el que produce dicha fuerza. Vamos a describir en esta sección otra posibilidad

Consideremos una varilla que puede girar en el plano horizontal con velocidad angular Ω constante alrededor de un eje perpendicular a la varilla. La varilla tiene dos muelles de constante k unidos a un anillo de masa m que puede desplazarse a lo largo de la varilla. Los extremos de los muelles están fijados a los extremos de la varilla tal como puede se puede ver en la figura

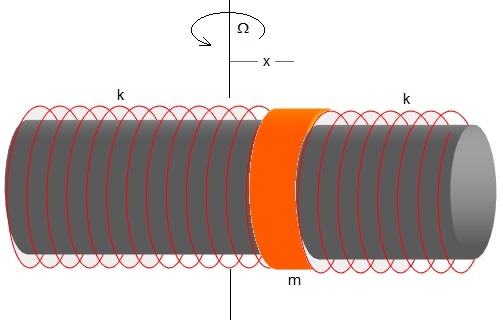
Representamos las fuerzas sobre el anillo de masa m en el instante t, cuando se ha desplazado x del eje de rotación y lleva una velocidad dx/dt

Para que el problema sea más simple, supondremos que el dispositivo está en el espacio, el peso del anillo mg y la reacción N de la varilla se consideran despreciables

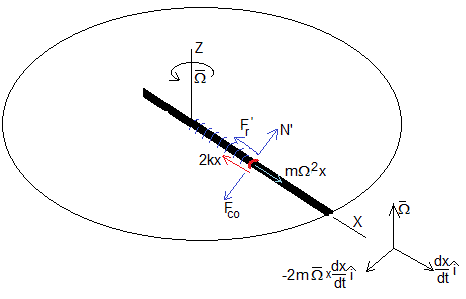
• Las fuerzas que ejercen los muelles elásticos, 2kx

• La fuerza centrífuga, $-m\Omega \widehat{k}\times \left(\Omega \widehat{k}\times x\widehat{i}\right)$, de módulo mΩ²x, ambas en la dirección radial

• La fuerza de Coriolis, $\overrightarrow{F_{co}}=-2m\left(\Omega \widehat{k}\times \frac{dx}{dt}\widehat{i}\right)$ es perpendicular a la varilla y su sentido se indica en la figura. La reacción N' o fuerza que ejerce la varilla sobre el anillo es de sentido contrario. $N\text{'}=2m\Omega \frac{dx}{dt}$

• Si hay rozamiento, la fuerza F'_r=μ_kN' es de sentido opuesto a la velocidad del anillo

Cuando el anillo está en resposo dx/dt=0, N'=0, la fuerza de rozamiento es nula. No hay fuerza de rozamiento estática

La ecuación del movimiento en el Sistema de Referencia no inercial (en rotación) de la varilla es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-2kx+m{\Omega }^{2}x-{\mu }_{k}N\text{'}\hfill \\ m\frac{d^{2}x}{d{t}^2}=-2kx+m{\Omega }^{2}x-{\mu }_k\left(2m\Omega \frac{dx}{dt}\right)\hfill \\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\mathrm{0,}\{\begin{array}{l}\gamma ={\mu }_k\Omega \\ {\omega }_0^2=2\frac{k}{m}-{\Omega }^2\end{array}\hfill \end{array}}$

Nueva posición de equilibrio

El caso más sencillo se produce cuando las fuerzas que ejercen los muelles 2kx son iguales a la fuerza centrífuga, mΩ²x, es decir, ${\omega }_0^2=\mathrm{0,}{\Omega }_f=\sqrt{2\frac{k}{m}}$, donde Ω_f es la velocidad angular de rotación

${\displaystyle \begin{array}{l}\frac{dv}{dt}+2\gamma v=0\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}=-2\gamma {\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=v_0\exp (-2\gamma t)\end{array}}$

Como la velocidad v=dx/dt, integrando de nuevo, con la condición de que en el instante t=0, el anillo parte del origen x=0 con velocidad inicial v₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}dx}=v_0{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t)·dt}\\ x=\frac{v_0}{2\gamma }\left(1-\exp (-2\gamma t)\right)\end{array}}$

El anillo tiende hacia la posición final x_∞ sin oscilar, después de un tiempo t→∞

${\displaystyle x_{\infty }=\frac{v_0}{2\gamma }=\frac{v_0}{2\Omega {\mu }_k}=\frac{v_0}{2{\mu }_k}\sqrt{\frac{m}{2k}}}$

Oscilaciones, amortiguadas, críticas y sobreamortiguadas

Para que el anillo oscile se tiene que cumplir que la frecuencia natural ω₀>0, es decir, la velocidad angular de rotación Ω<Ω_f

• Amortiguada

Para que la oscilación sea amortiguada γ<ω₀.

La ecuación de una oscilación amortiguada, con las condiciones iniciales t=0, x=0, y dx/dt=v₀ es

${\displaystyle x=\exp (-\gamma t)\frac{v_0}{\omega }\sin \left(\omega t\right),\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

• Crítica

La velocidad angular crítica Ω_c es aquella para la que se cumple γ=ω₀

${\displaystyle {\mu }_k^2{\Omega }^2=2\frac{k}{m}-{\Omega }^2,{\Omega }_c=\sqrt{\frac{2k}{m\left(1+{\mu }_k^2\right)}}}$

La ecuación de una oscilación crítica, con las condiciones iniciales t=0, x=0, y dx/dt=v₀ es

${\displaystyle x=v_{0}t\exp \left(-\gamma t\right)}$

• Sobreamortiguada

La ecuación de una oscilación sobreamortiguada, con las condiciones iniciales t=0, x=0, y dx/dt=v₀ es

${\displaystyle x=\exp (-\gamma t)\frac{v_0}{\omega }\sinh \left(\omega t\right),\omega =\sqrt{{\gamma }^2-{\omega }_0^2}}$

Ejemplo

Representamos el desplazamiento x de un anillo en función del tiempo t para varias velocidades angulares de rotación Ω. Los datos son

• masa, m=1 kg
• constante elástica de los muelles, 2k= 1 N/m
• coeficiente cinético, μ_k=1
• posición inicial del anillo, x₀=0
• velocidad inicial del anillo v₀=1 m/s

para los cuatro casos siguientes: la velocidad angular de rotación es Ω=0.1, $\frac{1}{\sqrt{2}}$, 0.9 y 1 rad/s

mu=1; %coeficiente cinético
v0=1; %velocidad inicial
m=1; %masa
k=0.5; %constante elástica
hold on

W=0.1; %amortiguado
gamma=mu*W;
w0=sqrt(2*k-W^2);
w=sqrt(w0^2-gamma^2);
fplot(@(t) v0*exp(-gamma*t).*sin(w*t)/w,[0,30])

W=1/sqrt(2); %crítica
gamma=mu*W;
fplot(@(t) v0*t.*exp(-gamma*t),[0,30])

W=0.9; %sobreamortiguado
gamma=mu*W;
w0=sqrt(2*k-W^2);
w=sqrt(gamma^2-w0^2);
fplot(@(t) v0*exp(-gamma*t).*sinh(w*t)/w,[0,30])

W=1; %nueva posición de equilibrio
w0=0;
gamma=mu*W;
fplot(@(t) v0*(1-exp(-2*gamma*t))/(2*gamma),[0,30])
hold off
legend('amortiguado','sobreamortiguado','nuevo equilibrio','location', 'best')
xlabel('t')
ylabel('x')
grid on
title('Desplazamiento')

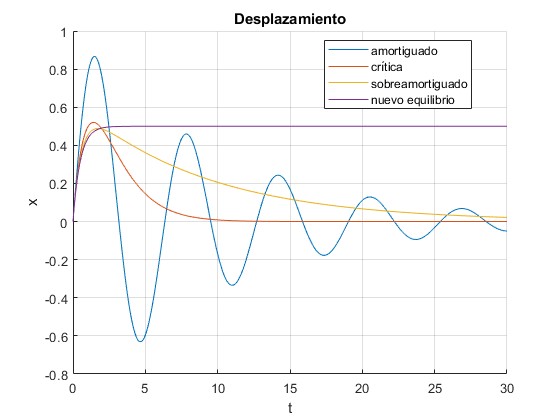
Cuando la velocidad angular de rotación, Ω>Ω_f

A medida que incrementamos la velocidad angular de rotación Ω, pasamos de oscilaciones amortiguadas, Ω<Ω_c, a críticas, Ω=Ω_c, a sobreamortiguadas, Ω>Ω_c. En el límite, cuando Ω=Ω_f, al nuevo estado de equilibrio.

En este apartado estudiamos el caso Ω>Ω_f

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}-{\omega }_0^{2}x=\mathrm{0,}\{\begin{array}{l}{\omega }_0^2={\Omega }^2-2\frac{k}{m}\\ \gamma ={\mu }_k\Omega \end{array}}$

Las raíces de la ecuación característica son

${\displaystyle s^2+2\gamma s-{\omega }_0^2=\mathrm{0,}\{\begin{array}{l}{s}_1=-\gamma +\sqrt{{\gamma }^2+{\omega }_0^2}\\ s_2=-\gamma -\sqrt{{\gamma }^2+{\omega }_0^2}\end{array}}$

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}x=A\exp \left((-\gamma +\omega )t\right)+B\exp \left((-\gamma -\omega )t\right)=\exp (-\gamma t)\left\{A\exp (\omega t)+B\exp (-\omega t)\right\}\\ \omega =\sqrt{{\omega }_0^2+{\gamma }^2}\end{array}}$

Derivando con respecto del tiempo obtenemos la velocidad

${\displaystyle \frac{dx}{dt}=-\gamma \exp (-\gamma t)\left\{A\exp (\omega t)+B\exp (-\omega t)\right\}+\omega \exp (-\gamma t)\left\{A\exp (\omega t)-B\exp (-\omega t)\right\}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}t=\mathrm{0,}\{\begin{array}{l}x=x_0\\ \frac{dx}{dt}=v_0\end{array}\\ \{\begin{array}{l}{x}_0=A+B\\ v_0=-\gamma \left(A+B\right)+\omega \left(A-B\right)\end{array}\\ A=\frac{v_0+x_0\left(\gamma +\omega \right)}{2\omega },B=\frac{-v_0+x_0\left(\omega -\gamma \right)}{2\omega }\end{array}}$

La posición del anillo x es

${\displaystyle x=\frac{\exp (-\gamma t)}{2\omega }\left\{\left(v_0+x_0\left(\gamma +\omega \right)\right)\exp (\omega t)+\left(-v_0+x_0\left(\omega -\gamma \right)\right)\exp (-\omega t)\right\}}$

Consideramos dos casos particulares

• El anillo parte del origen x₀=0, con velocidad v₀

${\displaystyle x=\frac{v_0}{\omega }\exp (-\gamma t)\sinh (\omega t)}$

• El anillo parte en reposo, v₀=0, desde la posición x₀

${\displaystyle \begin{array}{l}x=\frac{\exp (-\gamma t)}{2\omega }{x}_0\left\{\left(\gamma +\omega \right)\exp (\omega t)+\left(\omega -\gamma \right)\exp (-\omega t)\right\}\\ x=\frac{x_0}{\omega }\exp (-\gamma t)\left\{\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right\}\end{array}}$

Representamos el desplazamiento x de un anillo en función del tiempo t . Los datos son

• masa, m=1 kg
• constante elástica de los muelles, 2k= 1 N/m
• coeficiente cinético, μ_k=1
• velocidad angular de rotación Ω=1.5 rad/s
• posición inicial del anillo, x₀=0.2, en reposo, v₀=0
• velocidad inicial del anillo v₀=0.5 m/s en el origen x₀=0

mu=1; %coeficiente cinético
m=1; %masa
k=0.5; %constante elástica
hold on
W=1.5; %velocidad angular de rotación W>Wf
gamma=mu*W;
w0=sqrt(W^2-2*k/m);
w=sqrt(gamma^2+w0^2);

v0=0.5; %velocidad inicial
f=@(t) v0*exp(-gamma*t).*sinh(w*t)/w;
g=@(t) f(t)-1;
tf=fzero(g,[0,10]);
fplot(f,[0,tf])

x0=0.1; %posición inicial
f=@(t) x0*exp(-gamma*t).*(gamma*sinh(w*t)+w*cosh(w*t))/w;
g=@(t) f(t)-1;
tf=fzero(g,[0,10]);
fplot(f,[0,tf])
hold off
legend('velocidad','posición','location', 'best')
xlabel('t (s)')
ylabel('x (m)')
grid on
title('Desplazamiento')

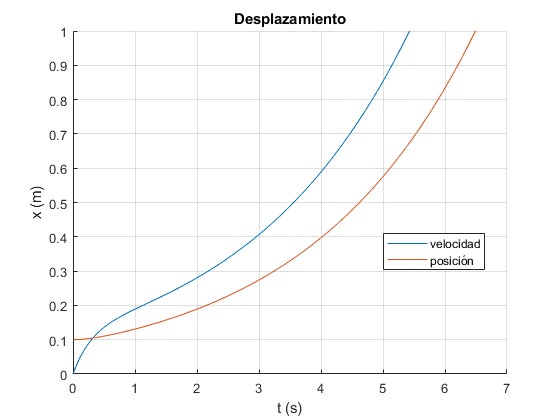
El tiempo final t_f se obtiene cuando x=1, que es el desplazamiento máximo del anillo. Para calcular este tiempo, resolvemos la ecuación transcendente empleando la función fzero de MATLAB

Posible ampliación

Si tenemos en cuenta el peso mg del anillo y la reacción N=mg de la varilla. Tendríamos además, una fuerza de rozamiento constante F_r=μ_kN para añadir a la ecuación del movimiento

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-2kx+m{\Omega }^{2}x-{\mu }_k\left(2m\Omega \frac{dx}{dt}\right)-{\mu }_{k}N\\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+\left(2\frac{k}{m}-{\Omega }^2\right)x=-{\mu }_{k}g\end{array}}$

Un caso análogo se estudia en la página titulada Oscilaciones amortiguadas combinación de una fuerza de rozamiento constante y otra proporcional a la velocidad

Actividades

Se introduce

• la velocidad angular de rotación, Ω en el control titulado Velocidad angular hasta un máximo de Ω_f=1 rad/s

Se han fijado los parámetros

• masa, m=1 kg
• constante elástica de los muelles, 2k= 1 N/m
• coeficiente cinético, μ_k=1
• posición inicial del anillo, x₀=0
• velocidad inicial del anillo v₀=1 m/s

En la parte superior izquierda, se proporcionan los datos del tiempo t y el desplzamiento x del anillo

Se pulsa el botón titulado Nuevo.

Referencias

Dejan M. Djokić. Dry Friction Camouflaged in Viscous Drag. THE PHYSICS TEACHER, Vol.58, May 2020, pp. 340-341

Carl E. Mungan. Letters to the editor. THE PHYSICS TEACHER, Vol.58, November 2020, pp. 532-533