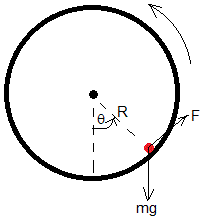
En el instante t=0, la jaula está en reposo y la ardilla en la parte inferior.

En el instante t la ardilla forma un ángulo θ con la vertical.

Sea F la fuerza de rozamiento entre la ardilla y la jaula. La ecuación del movimiento de la ardilla es

${\displaystyle mR\frac{d^2\theta }{d{t}^2}=F-mg\sin \theta }$

La ecuación del movimiento de rotación de la jaula alrededor de su eje, teniendo en cuenta el rozamiento en el eje cuyo momento es proporcional a la velocidad angular M_r=-k·dφ/dt es

${\displaystyle I\frac{d^2\phi }{d{t}^2}=-FR-k\frac{d\phi }{dt}}$

Para una jaula cilíndrica I=MR², siendo M la masa de la jaula

Dado que la ardilla se mueve con velocidad constante v₀ relativa a la jaula

${\displaystyle R\frac{d\theta }{dt}-R\frac{d\phi }{dt}=v_0}$

Lo que implica que las aceleraciones angulares de ambos cuerpos son las mismas.

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{d^2\phi }{d{t}^2}}$

Movimiento de la ardilla

Eliminando la cantidad desconocida F en sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\left(I+m{R}^2\right)\frac{d^2\theta }{d{t}^2}=-mgR\sin \theta -k\left(\frac{d\theta }{dt}-\frac{v_0}{R}\right)\\ \frac{d^2\theta }{d{t}^2}+\frac{k}{I+m{R}^2}\frac{d\theta }{dt}+\frac{mgR}{I+m{R}^2}\sin \theta =\frac{k}{I+m{R}^2}\frac{v_0}{R}\end{array}}$

Que podemos expresar de forma más compacta

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\sin \theta =f\\ 2\gamma =\frac{k}{I+m{R}^2}{\omega }_0^2=\frac{mgR}{I+m{R}^2}f=\frac{k}{I+m{R}^2}\frac{v_0}{R}\end{array}}$

La posición final de la ardilla se alcanza cuando su velocidad y aceleración se hacen cero, dθ/dt=0, d²θ/dt²=0.

${\displaystyle \begin{array}{l}{\omega }_0^2\sin {\theta }_{\infty }=f\\ \sin {\theta }_{\infty }=\frac{k{v}_0}{mg{R}^2}\end{array}}$

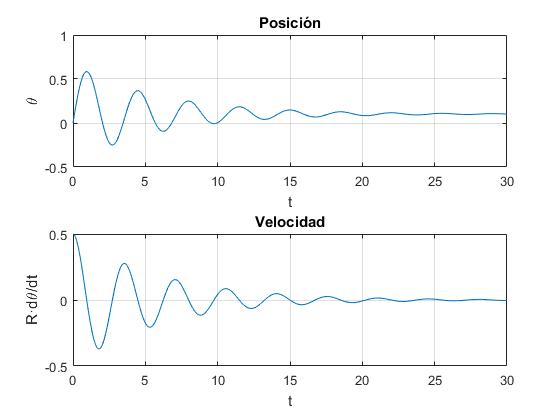
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=0, y dθ/dt=v₀/R. Representamos la posición θ y velocidad R·dθ/dt de la ardilla en función del tiempo t

m=0.2; %masa ardilla
R=0.5; %radio de la jaula
I=1*R^2; % Momento de inercia de la jaula , masa 1 kg,
k=0.1; %coeficiente de rozamiento
v0=0.5; %velocidad relativa de la ardilla respecto de la jaula
g=k/(2*(I+m*R^2)); %constante de amortiguación
w0=sqrt(m*9.8*R/(I+m*R^2)); %frecuencia propia
f=k*v0/(R*(I+m*R^2)); %término constante

fg=@(t,x) [x(2);-2*g*x(2)-w0*w0*sin(x(1))+f]; 
[t,x]=ode45(fg,[0,30],[0,v0/R]);

subplot(2,1,1)
plot(t,x(:,1)) %tiempo, posición
grid on
xlabel('t')
ylabel('\theta');
title('Posición')

subplot(2,1,2)
plot(t,x(:,2)*R) %tiempo,velocidad
grid on
xlabel('t')
ylabel('R·d\theta/dt');
title('Velocidad')

La posición final de la ardilla es

>> asin(f/w0^2)
ans =    0.1022

Movimiento de la jaula

Como la ardilla se mueve con velocidad relativa constante v₀ respecto de la jaula. Sus posiciones están relacionadas de forma similar a sus velocidades

${\displaystyle \phi =\theta -\frac{v_0}{R}t}$

Se ha suspuesto, que en el instante t=0, φ=0

Balance energético

El trabajo de la fuerza interna F que realiza la ardilla al desplazarse sobre la jaula con velocidad v₀, se invierte en energía cinética y potencial de la ardilla, en energía cinética de rotación de la jaula y otra parte, se disipa en el eje en forma de calor debido al rozamiento.

El trabajo realizado por la fuerza interna F, que se desplaza ds=v₀dt sobre la jaula es

${\displaystyle W_1={\displaystyle \underset{0}{\overset{t}{\int }}F}ds=v_0{\displaystyle \underset{0}{\overset{t}{\int }}F}dt}$

Conocida la posición θ(t) de la ardilla y su velocidad angular dθ/dt, calculamos la aceleración angular dθ²/dt², mediante la ecuación diferencial del movimiento

${\displaystyle \frac{d^2\theta }{d{t}^2}=f-2\gamma \frac{d\theta }{dt}-{\omega }_0^2\sin \theta }$

Calculamos la fuerza interna F mediante la expresión (véase al principio de la página)

${\displaystyle F=mR\frac{d^2\theta }{d{t}^2}+mg\sin \theta }$

El procedimiento ode45 de MATLAB nos proporciona el vector tiempo t, el vector posición angular x(:,1) y el vector velocidad angular x(:,2). Para calcular el trabajo de forma numérica, a partir del vector fuerza F y el vector tiempo t, se utiliza la función trapz de MATLAB

fuerza=m*R*(-2*g*x(:,2)-w0^2*sin(x(:,1))+f)+m*9.8*sin(x(:,1));
W1=trapz(t,fuerza*v0); %trabajo de la fuerza

La energía cinética de la ardilla en el instante t es

${\displaystyle E_{k1}=\frac{1}{2}m{\left(R\frac{d\theta }{dt}\right)}^2}$

La energía potencial de la ardilla en dicho instante es, tomando como nivel de referencia el eje de la jaula

${\displaystyle E_{p1}=-mgR\cos \theta }$

La energía cinética de rotación de la jaula es

${\displaystyle E_{k2}=\frac{1}{2}I{\left(\frac{d\phi }{dt}\right)}^2\frac{d\phi }{dt}=\frac{d\theta }{dt}-\frac{v_0}{R}}$

La última expresión es la relación entre las velocidades angulares de la ardilla y la jaula.

La energía final en el instante t es

${\displaystyle E=\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}I{\left(\frac{d\theta }{dt}-\frac{v_0}{R}\right)}^2-mgR\cos \theta }$

Ek_ardilla=m*R*R*x(end,2)^2/2;
v_phi=x(:,2)-v0/R; %velocidad angular de la jaula
Ek_jaula=I*v_phi(end)^2/2;
Ep=-m*9.8*R*cos(x(end,1));
E_fin=Ek_ardilla+Ek_jaula+Ep;

La energía inicial en el instante t=0, es la cinética de la ardilla moviéndose con velocidad v₀ en el interior de la jaula inicialmente en reposo, sumada a la energía potencial, tomando como referencia la altura del eje de la jaula.

${\displaystyle E_0=\frac{1}{2}m{v}_0^2-mgR}$

E_ini=m*v0^2/2-m*9.8*R;

Finalmente, el trabajo de la fuerza de rozamiento en el eje de la jaula.

${\displaystyle W_2={\displaystyle \underset{0}{\overset{t}{\int }}\left(-k\frac{d\phi }{dt}\right)}d\phi =-k{{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{d\phi }{dt}\right)}}^{2}dt}$

v_phi=x(:,2)-v0/R; %velocidad angular de la jaula
W2=trapz(t,-k*v_phi.^2); %disipada en el eje

El balance energético se escribe: trabajo de las fuerzas internas igual a variación de energía del sistema

${\displaystyle W_1+W_2=E-E_0}$

El código que se añade al procedimiento numérico es

.... procedimiento numérico
fuerza=m*R*(-2*g*x(:,2)-w0^2*sin(x(:,1))+f)+m*9.8*sin(x(:,1));
W1=trapz(t,fuerza*v0); %trabajo de la fuerza F
Ek_ardilla=m*R*R*x(end,2)^2/2; %cinética de la ardilla
v_phi=x(:,2)-v0/R; %velocidad angular de la jaula
W2=trapz(t,-k*v_phi.^2); %energía disipada en el eje
Ek_jaula=I*v_phi(end)^2/2; %cinética de la jaula
Ep=-m*9.8*R*cos(x(end,1)); %potencial de la ardilla
E_ini=m*v0^2/2-m*9.8*R; %energía inicial
E_fin=Ek_ardilla+Ek_jaula+Ep; %energía final

Comprobamos el balance energético

>> W1+W2
ans =    0.1066
>> E_fin-E_ini
ans =    0.1074

Oscilaciones amortigudas

Consideremos que las oscilaciones tienen pequeña amplitud, de modo que podemos hacer la aproximación sinθ≈θ

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =f}$

La solución particular de la ecuación diferencial es

${\displaystyle {\theta }_1=\frac{f}{{\omega }_0^2}}$

La solución de la homogénea es de la forma

${\displaystyle {\theta }_2=e^{-\gamma t}\left(A\sin (\omega t)+B\cos (\omega t)\right)\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

La solución completa es

${\displaystyle \begin{array}{l}\theta =e^{-\gamma t}\left(A\sin (\omega t)+B\cos (\omega t)\right)+\frac{f}{{\omega }_0^2}\\ \frac{d\theta }{dt}=-\gamma e^{-\gamma t}\left(A\sin (\omega t)+B\cos (\omega t)\right)+e^{-\gamma t}\omega \left(A\cos (\omega t)-B\sin (\omega t)\right)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales. En el instante t=0, θ=0, dθ/dt=v₀/R.

${\displaystyle \begin{array}{l}\theta =e^{-\gamma t}\left\{\frac{1}{\omega }\left(\frac{v_0}{R}-\frac{\gamma f}{{\omega }_0^2}\right)\sin (\omega t)-\frac{f}{{\omega }_0^2}\cos (\omega t)\right\}+\frac{f}{{\omega }_0^2}\\ \frac{d\theta }{dt}=e^{-\gamma t}\left\{\frac{1}{\omega }\left(f-\frac{\gamma v_0}{R}\right)\sin (\omega t)+\frac{v_0}{R}\cos (\omega t)\right\}\end{array}}$

Cuando t→∞ tiende a infinito, la posición θ y la velocidad R·dθ/dt de la ardilla tienden a

${\displaystyle \begin{array}{l}{\theta }_{\infty }=\frac{f}{{\omega }_0^2}=\frac{k{v}_0}{mg{R}^2}\\ {\left(\frac{d\theta }{dt}\right)}_{\infty }=0\end{array}}$

La velocidad angular de rotación de la jaula cilíndrica tiende al valor constante v₀/R

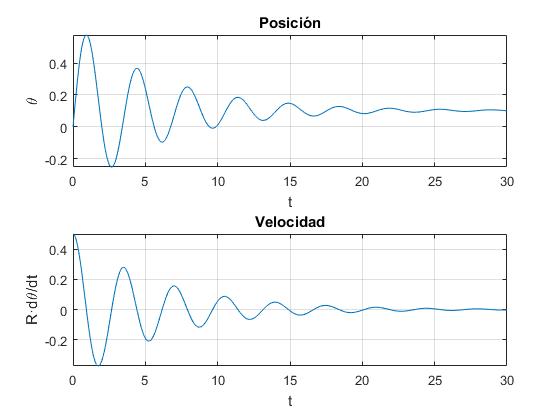
Representamos la posición θ y velocidad R·dθ/dt de la ardilla en función del tiempo t

m=0.2; %masa ardilla
R=0.5; %radio de la jaula
I=1*R^2; % Momento de inercia de la juala , masa 1 kg,
k=0.1; %coeficiente de rozamiento
v0=0.5; %velocidad relativa
g=k/(2*(I+m*R^2)); 
w0=sqrt(m*9.8*R/(I+m*R^2)); %frecuencia propia
f=k*v0/(R*(I+m*R^2)); %término constante
w=sqrt(w0^2-g^2); %frecuencia de la oscilación amortiguada

subplot(2,1,1)
%posición
th=@(t) exp(-g*t).*((v0/R-g*f/w0^2)*sin(w*t)/w-f*cos(w*t)/w0^2)+f/w0^2;
fplot(th,[0,30]) %tiempo, posición
grid on
xlabel('t')
ylabel('\theta');
title('Posición')

subplot(2,1,2)
%velocidad
D_th=@(t) R*exp(-g*t).*((f-g*v0/R)*sin(w*t)/w+v0*cos(w*t)/R);
fplot(D_th,[0,30]) %tiempo, posición
grid on
xlabel('t')
ylabel('R·d\theta/dt');
title('Velocidad')

Balance energético

Partimos de la posición,velocidad angular y aceleración angular de la ardilla en función del tiempo

${\displaystyle \begin{array}{l}\theta =e^{-\gamma t}\left\{\frac{1}{\omega }\left(\frac{v_0}{R}-\frac{\gamma f}{{\omega }_0^2}\right)\sin (\omega t)-\frac{f}{{\omega }_0^2}\cos (\omega t)\right\}+\frac{f}{{\omega }_0^2}\\ \frac{d\theta }{dt}=e^{-\gamma t}\left\{\frac{1}{\omega }\left(f-\frac{\gamma v_0}{R}\right)\sin (\omega t)+\frac{v_0}{R}\cos (\omega t)\right\}\\ \frac{d^2\theta }{d{t}^2}=-\frac{1}{\omega }{e}^{-\gamma t}\left(\frac{mg{v}_0}{I+m{R}^2}\right)\sin (\omega t)\end{array}}$

Calculamos la expresión de la fuerza interna F suponiendo que la amplitud es pequeña sinθ≈θ

${\displaystyle F=mR\frac{d^2\theta }{d{t}^2}+mg\theta }$

Calculamos el trabajo W₁ de la fuerza interna F y el trabajo W₂ de la fuerza de rozamiento en el eje

${\displaystyle \begin{array}{l}{W}_1=v_0{\displaystyle \underset{0}{\overset{t}{\int }}Fdt}\\ W_2=-k{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{d\phi }{dt}\right)}^{2}dt}\frac{d\phi }{dt}=\frac{d\theta }{dt}-\frac{v_0}{R}\end{array}}$

La energía inicial es la suma de la cinética de la ardilla y la cinética de la jaula. Como el ángulo θ es pequeño cosθ≈1, la energía potencial de la ardilla apenas cambia

${\displaystyle E_k=\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}I{\left(\frac{d\phi }{dt}\right)}^2}$

La energía inicial en el instante t=0, es la cinética de la ardilla moviéndose con velocidad v₀ en el interior de la jaula inicialmente en reposo.

${\displaystyle E_0=\frac{1}{2}m{v}_0^2}$

El balance energético se escribe

${\displaystyle W_1+W_2=E-E_0}$

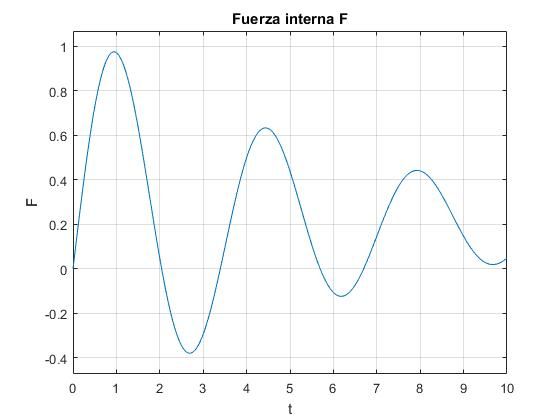
Para comprobar el balance energético en cualquier instante, las expresiones algebraicas que se obtienen son muy largas por lo que nos valdremos del Math Symbolic de MATLAB. Mediante ezplot podemos representar nuevamente, la posición, velocidad o aceleración angular de la ardilla o de la jaula. Por ejemplo, representamos la fuerza interna F en función del tiempo t

I=1*R^2; % Momento de inercia de la jaula , masa 1 kg,
k=0.1; %coeficiente de rozamiento
v0=0.5; %velocidad relativa de la ardilla respecto de la jaula

g=k/(2*(I+m*R^2)); %constante de amortiguación
w0=sqrt(m*9.8*R/(I+m*R^2)); %frecuencia propia
f=k*v0/(R*(I+m*R^2)); %término constante
w=sqrt(w0^2-g^2); %frecuencia de la oscilación amortiguada
%th_equi=k*v0/(m*9.8*R^2);

syms t;
%posición de la ardilla
th=exp(-g*t)*((v0/R-g*f/w0^2)*sin(w*t)/w-f*cos(w*t)/w0^2)+f/w0^2; 
w_th=diff(th); %velocidad angular de la ardilla
w_jaula=w_th-v0/R; %velocidad angular de la jaula
F=m*R*diff(w_th)+m*9.8*th; %fuerza

tf=10; %tiempo final, cambiar
W1=int(F*v0,0,tf);
W2=int(-k*w_jaula^2,0,tf);
vf=R*subs(w_th,t,tf); %velocidad final de la ardilla
wf=subs(w_jaula,t,tf); %velocidad angular final de la jaula
E_fin=m*vf*vf/2+I*wf*wf/2; %energía final
E_ini=m*v0^2/2; %energía inicial

ezplot(F,[0,tf])
xlabel('t')
ylabel('F')
grid on
title('Fuerza interna F')

Comprobamos el balance energético

>> double(W1+W2)
ans =    0.0741
>> double(E_fin-E_ini)
ans =    0.0741

Balance energético en el estado estacionario

En el estado estacionario, la posición de la ardilla es θ_∞, su velocidad y aceleración angular son nulas dθ/dt=0 y d²θ/dt²=0. La fuerza F de rozamiento entre la ardilla y la jula es F=mgsinθ_∞, F≈mgθ_∞, suponiendo que el ángulo es pequeño.

La velocidad angular de rotación de la jaula cilíndrica es constante e igual a v₀/R.

El trabajo de la fuerza F durante un intervalo de tiempo Δt, se transforma íntegramente en energía disipada en el eje de la jaula.

${\displaystyle W_1=F(v_0\Delta t)=mg{\theta }_{\infty }{v}_0\Delta t=mg\frac{k{v}_0}{mg{R}^2}{v}_0\Delta t=\frac{k{v}_0^2}{R^2}\Delta t}$

El trabajo del momento de la fuerza de rozamiento en el eje, es el producto del momento de la fuerza por el ángulo girado en el tiempo Δt, W=M_r·φ

${\displaystyle W_2=-\left(k\frac{v_0}{R}\right)\left(\frac{v_0}{R}\Delta t\right)=-k\frac{v_0^2}{R^2}\Delta t}$

Obtenemos el mismo resultado

Actividades

Se introduce

• La masa m de la ardilla, en el control titulado Masa ardilla
• La velocidad constante v₀ de la ardilla, respecto de la jaula, en el control titulado Velocidad relativa
• La constante k de proporcionalidad del momento de la fuerza de rozamiento, en el control titulado Constante k
• La masa de la jaula se ha fijado en M=1 kg
• El radio de la jaula se ha fijado en R=0.5 m

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la ardilla (un punto de color rojo) y de la jaula. En la parte izquierda se proporcionan los datos de

• El tiempo t
• La posición angular θ de la ardilla, una regla graduada nos permite medir su posición final en grados
• El ángulo girado φ por la jaula
• La velocidad de la ardilla, R·dθ/dt, que tiende a cero, cuando alcanza la posición final (después de un tiempo teóricamente infinito)
• La velocidad angular de rotación de la jaula cilíndrica R·dφ/dt tiende al valor constante v₀/R

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1169, pp. 273-275