La ecuación diferencial que describe un oscilador forzado bajo la acción de una fuerza F(t) es

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{F(t)}{m}}$

• donde ω₀ es la frecuencia natural o propia del oscilador
• F(t) es la fuerza oscilante
• γ es la constante de amortiguamiento, γ<ω₀

Los casos más simples de fuerza F(t) son los siguientes:

• Cuando F(t)=F₀ es una fuerza constante, la solución particular de la ecuación diferencial tiene la forma

x=C

Obtenemos el valor de C haciendo que cumpla la ecuación diferencial lineal completa

${\displaystyle C=\frac{F_0}{m{\omega }_0^2}}$

• Cuando F(t)=F₀·cos(ω_ft), siendo ω_f es la frecuencia angular de la fuerza oscilante, la solución particular de la ecuación diferencial tiene la forma

x=A_ccos(ω_f t)+B_csin(ω_f t)

Obtenemos los valores de A_c y B_c haciendo que cumpla la ecuación diferencial lineal completa

${\displaystyle A_c=\frac{F_0}{m}\frac{{\omega }_0^2-{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{B}_c=\frac{F_0}{m}\frac{2\gamma {\omega }_f}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}}$

• Cuando F(t)=F₀·sin(ω_ft), la solución particular de la ecuación diferencial tiene la forma

x=A_scos(ω_f t)+B_ssin(ω_f t)

Obtenemos los valores de A_s y B_s haciendo que cumpla la ecuación diferencial lineal completa

${\displaystyle A_s=-\frac{F_0}{m}\frac{2\gamma {\omega }_f}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{B}_s=\frac{F_0}{m}\frac{{\omega }_0^2-{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}}$

Superposición

Cuando una fuerza F(t) es periódica de periodo P=2π/ω, se puede representar en forma de una suma infinita de funciones armónicas

${\displaystyle F(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos (k\omega t)+b_k\sin (k\omega t)\right)}}$

donde a₀ a₁ ...a_k ... y b₁ b₂ .... b_k .... son los denominados coeficientes de Fourier.

${\displaystyle \begin{array}{l}{a}_k=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}F(t)\cos (k\omega t)}·dtk=\mathrm{0,1,2....}\\ b_k=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}F(t)\sin (k\omega t)}·dtk=\mathrm{1,2....}\end{array}}$

Aplicando el principio de superposición, la solución de la ecuación diferencial en el estado estacionario

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{F(t)}{m}}$

es la suma de las soluciones en el estado estacionario de las ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{a_0}{2m}\\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{a_k}{m}\cos (k\omega t)\\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{b_k}{m}\sin (k\omega t)\end{array}}$

Teniendo en cuenta que la frecuencia de la fuerza oscilante ω_f =kω, y que las amplitudes de la fuerza oscilante son F₀=a_k ó F₀=b_k. Las soluciones en el estado estacionario de cada una de las tres ecuaciones diferenciales que denominaremos, x₀, x_ck (coseno), x_sk (seno) respectivamente, son

${\displaystyle \begin{array}{l}{x}_0=\frac{a_0}{2m{\omega }_0^2}\\ x_{ck}=\frac{a_k}{m}\frac{{\omega }_0^2-k^2{\omega }^2}{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\cos (k\omega t)+\\ \frac{a_k}{m}\frac{2\gamma k\omega }{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\sin (k\omega t)\\ x_{sk}=-\frac{b_k}{m}\frac{2\gamma k\omega }{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\cos (k\omega t)+\\ \frac{b_k}{m}\frac{{\omega }_0^2-k^2{\omega }^2}{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\sin (k\omega t)\end{array}}$

El comportamiento del oscilador en el estado estacionario bajo la acción de la fuerza periódica F(t) es la suma

${\displaystyle \begin{array}{l}x=x_0+{\displaystyle \sum _{k=1}^{\infty }{x}_{ck}+}{\displaystyle \sum _{k=1}^{\infty }{x}_{sk}}=\\ \frac{1}{m}\left(\frac{a_0}{2{\omega }_0^2}+{\displaystyle \sum _{k=1}^{\infty }\left(\left(a_k{A}_k-b_k{B}_k\right)\cos (k\omega t)+\left(a_k{B}_k+b_k{A}_k\right)\sin (k\omega t)\right)}\right)\\ A_k=\frac{{\omega }_0^2-k^2{\omega }^2}{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}{B}_k=\frac{2\gamma k\omega }{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\end{array}}$

Ejemplos

Fuerza periódica de simetría par

Sea la fuerza periódica F(t) de periodo P=2π/ω, de la figura

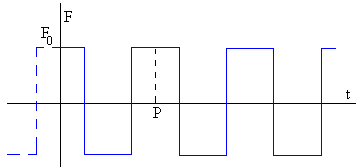
Como la función es simétrica, f(x)=f(-x), par, calculamos los coeficientes del desarrollo en serie de Fourier a_k ya que b_k=0

${\displaystyle \begin{array}{l}{a}_k=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}F(t)\cos (k\omega t)·dt=}\\ \frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/4}{\int }}{F}_0\cos (k\omega t)·dt}+{\displaystyle \underset{P/4}{\overset{3P/4}{\int }}(-F_0)\cos (k\omega t)·dt}+{\displaystyle \underset{3P/4}{\overset{P}{\int }}{F}_0\cos (k\omega t)·dt}\right)\\ =\frac{4F_0}{k\pi }{\left(-1\right)}^{\frac{k-1}{2}}k=\mathrm{1,3,5...}\end{array}}$

>> syms t P k;
>> ak=(2/P)*(int(cos(2*pi*k*t/P),t,0,P/4)-int(cos(2*pi*k*t/P),t,P/4,3*P/4)
+int(cos(2*pi*k*t/P),t,3*P/4,P));
>> subs(ak,k,sym('[1 2 3 4 5]'))
ans =[ 4/pi, 0, -4/(3*pi), 0, 4/(5*pi)]

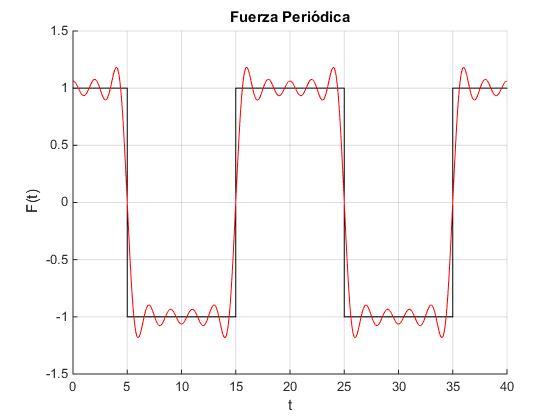
La función F(t) se expresa como suma de armónicos

${\displaystyle F(t)=F_0\left(\frac{4}{\pi }\cos (\omega t)-\frac{4}{3\pi }\cos (3\omega t)+\frac{4}{5\pi }\cos (5\omega t)-\mathrm{...}\right)}$

P=20;
F0=1;
f=0;
t=linspace(0,40,500);
hold on
xx=[0 5 5 15 15 20]; %un periodo
yy=[1 1 -1 -1 1 1];
x=[xx,xx+20]; %dos periodos
y=[yy,yy];
plot(x,y,'k')
for k=1:2:9 %seis términos
    f=f+(F0*4/pi)*(-1)^((k-1)/2)*cos(2*pi*k*t/P)/k;
end
plot(t,f,'r')
xlabel('t')
ylabel('F(t)')
title('Fuerza periódica')
grid on
hold off

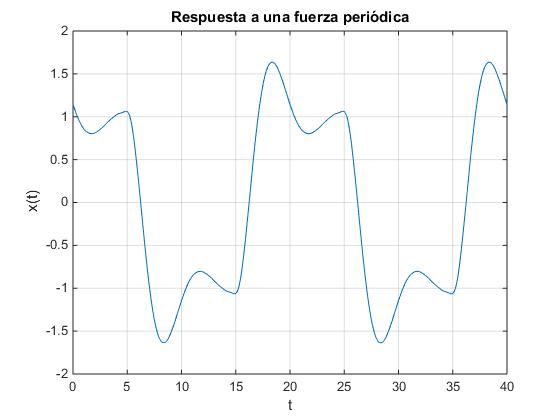
El comportamiento del oscilador en el estado estacionario bajo la acción de la fuerza periódica F(t) es la suma

${\displaystyle \begin{array}{l}x={\displaystyle \sum _{k=\mathrm{1,3,5..}}^{\infty }{x}_{ck}=}\\ \frac{F_0}{m}\frac{4}{\pi }{\displaystyle \sum _{k=\mathrm{1,3,5..}}^{\infty }\frac{{\left(-1\right)}^{\frac{k-1}{2}}}{k}\left(\begin{array}{l}\frac{{\omega }_0^2-k^2{\omega }^2}{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\cos (k\omega t)\\ +\frac{2\gamma k\omega }{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\sin (k\omega t)\end{array}\right)}\end{array}}$

w=pi/10; %frecuencia de la fuerza, P=20
w0=1; %frecuencia propia del oscilador
g=0.35; %coef. rozamiento
F0=1; %amplitud de la fuerza
m=1;  %masa
x=0;
t=linspace(0,40,500);
for k=1:2:21;  %diez términos del desarrollo en serie
    Ac=(w0^2-k^2*w^2)/((w0^2-k^2*w^2)^2+4*g^2*k^2*w^2);
    Bc=2*g*k*w/((w0^2-k^2*w^2)^2+4*g^2*k^2*w^2);
    x=x+(F0/m)*(4/pi)*((-1)^((k-1)/2)/k)*(Ac*cos(k*w*t)+Bc*sin(k*w*t));
end
plot(t,x)
xlabel('t');
ylabel('x(t)')
title('Respuesta a una fuerza periódica')
grid on

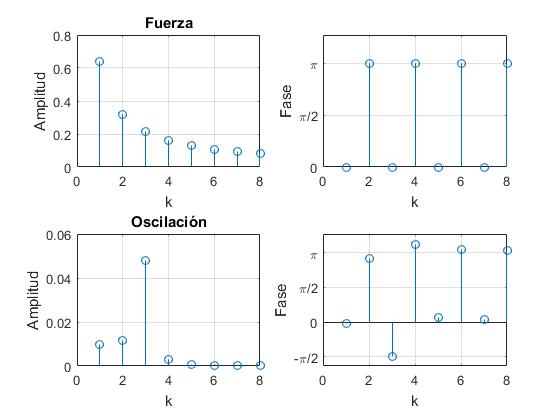
Expresamos la fuerza de la forma

${\displaystyle F(t)={\displaystyle \sum _{k=\mathrm{1,3,5,...}}^{\infty }{F}_k}\cos \left(k\omega t+{\phi }_k\right)}$

Para los términos k= 1, 5, 9, 13, ... la amplitud F_k es positiva y para los términos k= 3, 7, 11, ..., la amplitud es negativa. En el caso de amplitud negativa, podemos escribir una amplitud F_k positiva e incrementar la fase en π, cos(φ+π)=-cos(φ)

${\displaystyle \begin{array}{l}F(t)=F_0{\displaystyle \sum _{k=\mathrm{1,3,5,...}}^{\infty }{\left(-1\right)}^{\frac{k-1}{2}}\frac{4}{\pi k}}\cos \left(k\omega t\right)\\ F(t)=F_0{\displaystyle \sum _{k=\mathrm{1,3,5,...}}^{\infty }\frac{4}{\pi k}}\cos \left(k\omega t+\frac{\pi }{2}\left(1-{\left(-1\right)}^{\frac{k-1}{2}}\right)\right)\end{array}}$

Del mismo modo, expresamos x de la forma

${\displaystyle \begin{array}{l}x={\displaystyle \sum _{k=\mathrm{1,3,5...}}^{\infty }{A}_k\cos \left(k\omega t-{\phi }_k\right)}\\ A_k=\frac{F_0}{m}\frac{4}{\pi k}\frac{1}{\sqrt{{({\omega }_0^2-k^2{\omega }^2)}^2+4{\gamma }^2{k}^2{\omega }^2}}\tan {\phi }_k=\frac{2\gamma k\omega }{{\omega }_0^2-k^2{\omega }^2}\\ x={\displaystyle \sum _{k=\mathrm{1,3,5...}}^{\infty }{A}_k\cos \left(k\omega t-{\phi }_k+\frac{\pi }{2}\left(1-{\left(-1\right)}^{\frac{k-1}{2}}\right)\right)}\end{array}}$

Representamos, la fuerza periódica F(t), la amplitud F_k y su fase φ_k, el desplazamiento x(t) la amplitud A_k y su fase. Se suguiere probar para frecuencias de la fuerza oscilante ω=ω₀/k, con k=1, 3, 5,...

w0=1; %frecuencia propia del oscilador
w=w0/3; %frecuencia de la fuerza
g=0.35; %coef. rozamiento
k=1:2:11;

subplot(2,2,1)
stem(k,(4/pi)./k)
grid on
xlabel('k')
ylabel('Amplitud')
title('Fuerza')

subplot(2,2,2)
stem(k,rem((k-1)/2,2)*pi)
grid on
xlabel('k')
set(gca,'YTick',0:pi/2:pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi'})
ylabel('Fase')

subplot(2,2,3) %Amplitud
A=4./(pi*k.*((w0^2-k.^2*w^2).^2+4*g^2*k.^2*w^2));
stem(k,A)
grid on
xlabel('k')
ylabel('Amplitud')
title('Oscilación')

subplot(2,2,4) %resultante
phi=-atan(2*g*k*w./(w0^2-k.^2*w^2))+rem((k-1)/2,2)*pi;
stem(k,phi)
grid on
set(gca,'YTick',-pi:pi/2:3*pi/2)
set(gca,'YTickLabel',{'-\pi','-\pi/2','0','\pi/2','\pi','3\pi/2'})
xlabel('k')
ylabel('Fase')

Fuerza periódica de simetría impar

Sea la fuerza periódica F(t) de periodo P=2π, de la figura

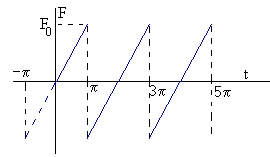
Como la función es antisimétrica, f(x)=-f(-x), impar, calculamos los coeficientes del desarrollo en serie de Fourier b_k ya que a_k=0

${\displaystyle \begin{array}{l}{b}_k=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}F(t)\sin (k\omega t)·dt=}\\ \frac{2}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\left(\frac{F_0}{\pi }t\right)\sin (kt)·dt}=\frac{F_0}{{\pi }^2}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}t\sin (kt)·dt}\\ =\frac{2F_0}{\pi }\frac{{\left(-1\right)}^{k+1}}{k}k=\mathrm{1,2,3...}\end{array}}$

>> syms k t;
>> bk=int((t*sin(k*t)),t,-pi,pi)/sym('pi')^2;
>> bk=simplify(bk)
bk =(2*(sin(pi*k) - pi*k*cos(pi*k)))/(pi^2*k^2)
>> subs(bk,k,sym('[1 2 3 4]'))
ans =[ 2/pi, -1/pi, 2/(3*pi), -1/(2*pi)]

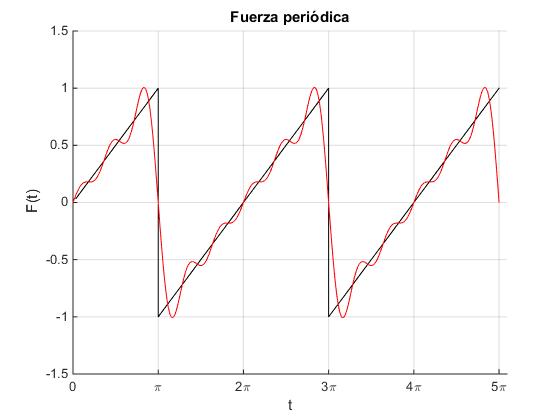
La función F(t) se expresa como suma de armónicos

${\displaystyle F(t)=\frac{2F_0}{\pi }\left(\sin (t)-\frac{1}{2}\sin (2t)+\frac{1}{3}\sin (3t)-\frac{1}{4}\sin (4t)\mathrm{...}\right)}$

F0=1;
f=0;
hold on
xx=linspace(-pi,pi,30); %un periodo
yy=F0*xx/pi;
x=[xx(xx>0),xx+2*pi,xx+4*pi]; 
y=[yy(xx>0),yy,yy];
plot(x,y,'k')
t=linspace(0,5*pi,300);
for k=1:5 %cinco términos
    f=f+(F0*2/pi)*(-1)^(k+1)*sin(k*t)/k;
end
plot(t,f,'r')
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})
xlabel('t')
ylabel('F(t)')
title('Fuerza periódica')
grid on
hold off

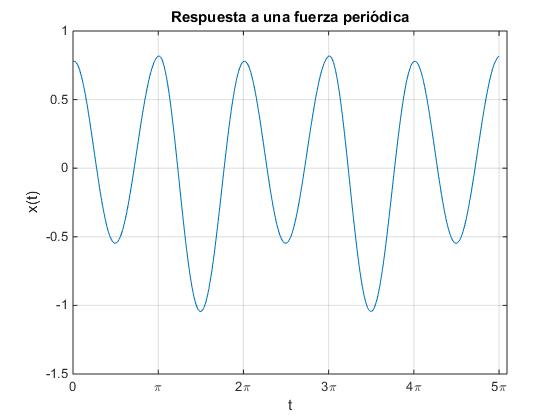
El comportamiento del oscilador en el estado estacionario bajo la acción de la fuerza periódica F(t) de periodo P=2π o frecuencia angular ω=1, es la suma

${\displaystyle \begin{array}{l}x={\displaystyle \sum _{k=\mathrm{1,2,3...}}^{\infty }{x}_{sk}=}\\ \frac{F_0}{m}\frac{2}{\pi }{\displaystyle \sum _{k=\mathrm{1,2,3..}}^{\infty }\frac{{\left(-1\right)}^{k+1}}{k}\left(\begin{array}{l}-\frac{2\gamma k\omega }{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\cos (k\omega t)\\ +\frac{{\omega }_0^2-k^2{\omega }^2}{{\left({\omega }_0^2-k^2{\omega }^2\right)}^2+4{\gamma }^2{k}^2{\omega }^2}\sin (k\omega t)\end{array}\right)}\end{array}}$

w=1; %frecuencia de la fuerza
w0=2; %frecuencia propia del oscilador
g=0.1; %coef. rozamiento
F0=1; %amplitud de la fuerza
m=1; %masa
x=0;
t=linspace(0,5*pi,500);
for k=1:40;
    As=-2*g*k*w/((w0^2-k^2*w^2)^2+4*g^2*k^2*w^2);
    Bs=(w0^2-k^2*w^2)/((w0^2-k^2*w^2)^2+4*g^2*k^2*w^2);
    x=x+(F0/m)*(2/pi)*((-1)^(k+1)/k)*(As*cos(k*w*t)+Bs*sin(k*w*t));
end
plot(t,x)
xlabel('t');
ylabel('x(t)')
title('Respuesta a una fuerza periódica')
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})
grid on  

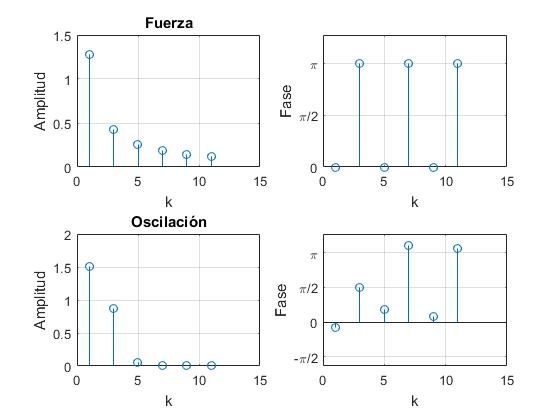
Expresamos la fuerza de la forma

${\displaystyle \begin{array}{l}F(t)={\displaystyle \sum _{k=1}^{\infty }{F}_k}\sin \left(kt+{\phi }_k\right)\\ F(t)=\frac{2F_0}{\pi }{\displaystyle \sum _{k=1}^{\infty }\frac{1}{k}}\sin \left(kt+\frac{\pi }{2}\left(1-{\left(-1\right)}^{k+1}\right)\right)\end{array}}$

Del mismo modo, expresamos x de la forma

${\displaystyle \begin{array}{l}x={\displaystyle \sum _{k=1}^{\infty }{A}_k\sin \left(kt-{\phi }_k\right)}\\ A_k=\frac{F_0}{m}\frac{2}{\pi k}\frac{1}{\sqrt{{\left({\omega }_0^2-k^2\right)}^2+4{\gamma }^2{k}^2}}\tan {\phi }_k=\frac{2\gamma k}{{\omega }_0^2-k^2}\\ x={\displaystyle \sum _{k=1}^{\infty }{A}_k\sin \left(kt-{\phi }_k+\frac{\pi }{2}\left(1-{\left(-1\right)}^{k+1}\right)\right)}\end{array}}$

Representamos, la fuerza periódica F(t), la amplitud F_k y su fase φ_k, el desplazamiento x(t) la amplitud A_k y su fase. Se suguiere probar para frecuencias propias ω₀=k, con k=1, 2, 3,...

w0=3; %frecuencia propia del oscilador
g=0.35; %coef. rozamiento
k=1:8;

subplot(2,2,1)
stem(k,(2/pi)./k)
grid on
xlabel('k')
ylabel('Amplitud')
title('Fuerza')

subplot(2,2,2)
stem(k,rem(k+1,2)*pi)
grid on
xlabel('k')
set(gca,'YTick',0:pi/2:pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi'})
ylabel('Fase')

subplot(2,2,3) %Amplitud
A=2./(pi*k.*((w0^2-k.^2).^2+4*g^2*k.^2));
stem(k,A)
grid on
xlabel('k')
ylabel('Amplitud')
title('Oscilación')

subplot(2,2,4) %resultante
phi=-atan(2*g*k./(w0^2-k.^2))+rem(k+1,2)*pi;
stem(k,phi)
grid on
set(gca,'YTick',-pi:pi/2:3*pi/2)
set(gca,'YTickLabel',{'-\pi','-\pi/2','0','\pi/2','\pi','3\pi/2'})
xlabel('k')
ylabel('Fase')