Movimiento de una caja sobre una cinta transportadora

Una caja de masa m está unida a un muelle de constante elástica k, se coloca sobre una cinta trasportadora que se mueve con velocidad constante v₀. El coeficiente estático entre la caja y la cinta es μ_s y el coeficiente cinético μ_k, con μ_s≥ μ_k.

Las fuerzas sobre la caja son:

El peso mg
La reacción de la cinta N=mg
La fuerza que ejerce el muelle deformado kx
La fuerza de rozamiento f_r

Vamos a estudiar cada una de las etapas del movimiento

Etapa inicial

Cuando la caja se encuentra en el origen, el muelle no está deformado

Si colocamos la caja en el origen la fuerza de rozamiento f_r lo mueve hacia la derecha con velocidad v₀, la deformación del muelle aumenta, la fuerza que ejerce el muelle aumenta, hasta que la fuerza de rozamiento alcanza su valor máximo f_r=μ_s·mg, tal como se muestra en la figura, esto sucede en la posición kx₀= μ_s·mg

$x_{0} = \frac{μ_{s} g}{ω^{2}} ω^{2} = \frac{k}{m}$

La caja desliza sobre la cinta

En este instante, ponemos a cero el cronómetro t=0

La fuerza de rozamiento vale f_r= μ_k·mg y tiene el mismo sentido que la velocidad relativa (v₀-v), o de sentido contrario a la velocidad relativa de la caja sobre la cinta. Como v≤v₀, el sentido de la fuerza de rozamiento es el mismo que el de la velocidad de la cinta (hacia la derecha).

La ecuación del movimiento del cuerpo es

ma=-kx+f_r

En forma de ecuación diferencial se escribe

$\frac{d^{2} x}{d t^{2}} + ω^{2} x = μ_{k} g$

Esta ecuación del movimiento nos recuerda la ecuación diferencial de un MAS, pero además tiene el término adicional μ_k·g

La solución de la ecuación diferencial es la suma de la homogénea (la ecuación de un MAS) más una constante C. Introduciendo la solución particular (la constante C) en la ecuación diferencial

ω²C= μ_k·g, C= μ_k·g/ω²

La solución completa de la ecuación diferencial es

$x = A \sin (ω t + φ) + \frac{μ_{k} g}{ω^{2}}$

La velocidad de la caja es

$v = \frac{d x}{d t} = A ω \cos (ω t + φ)$

La amplitud A y la fase inicial φ se calculan a partir de las condiciones iniciales. Ponemos el contador de tiempo a cero t=0, cuando la caja parte de la posición x₀= μ_s·g/ω², con velocidad v₀.

$\begin{array}{l} \frac{μ_{s} g}{ω^{2}} = A \cdot \sin φ + \frac{μ_{k} g}{ω^{2}} \\ v_{0} = A ω \cos φ \end{array}$

La posición x y la velocidad v de la caja son

$\begin{array}{l} x = \frac{1}{ω^{2}} (\sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}} \sin (ω t + φ) + μ_{k} g) tan φ = \frac{(μ_{s} - μ_{k}) g}{v_{0} ω} \\ v = \frac{1}{ω} \sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}} cos (ω t + φ) \end{array}$

La caja se mueve hacia la derecha de la posición inicial x₀, la fuerza que ejerce el muelle kx es mayor que la fuerza de rozamiento f_r= μ_k·mg, la velocidad de la caja disminuye hasta que se hace cero en el instante t tal que ωt+φ=π/2. La caja se encuentra en la posición de máximo desplazamiento hacia la derecha

$x_{1} = \frac{1}{ω^{2}} (\sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}} + μ_{k} g)$

A partir de este momento, la caja se mueve hacia la izquierda incrementando su velocidad, hasta que pasa por un valor máximo (en valor absoluto) cuando ωt+φ=π. La caja se encuentra en la posición

$x_{e} = \frac{μ_{k} g}{ω^{2}}$

y su velocidad es

$v = - \frac{1}{ω} \sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}}$

La caja se detiene v=0, en el instante t tal que ωt+φ=3π/2. El máximo desplazamiento de la caja hacia la izquierda es

$x_{2} = \frac{1}{ω^{2}} (- \sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}} + μ_{k} g)$

La caja se mueve hacia la derecha incrementando su velocidad hasta que se hace igual a la velocidad de la cinta v₀ en el instante t tal que

$\cos (ω t + φ) = \frac{v_{0} ω}{\sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}}} = \frac{1}{\sqrt{1 + \tan^{2} φ}} = \cos (2 π - φ)$

Igualando los argumentos ωt=2π-2φ. La posición de la caja x_d en este instante es

$x_{d} = \frac{1}{ω^{2}} (\sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}} + \sin (2 π - φ) + μ_{k} g) = \frac{g}{ω^{2}} (2 μ_{k} - μ_{s})$

Para llegar a estas expresiones, se han utilizado las relaciones

$sin φ = \frac{\tan φ}{\sqrt{1 + \tan^{2} φ}} cos φ = \frac{1}{\sqrt{1 + \tan^{2} φ}}$

El tiempo que dura la etapa de deslizamiento es ωt=2π-2φ

$t_{d} = \frac{2}{ω} (π - \arctan \frac{(μ_{s} - μ_{k}) g}{v_{0} ω})$

Empieza en la posición x₀=μ_s·g/ω² y termina en la posición x_d=(2μ_k-μ_s)·g/ω²

La caja se mueve con la cinta

La caja se mueve con velocidad constante desde la posición x_d hasta la posición x₀=μ_s·g/ω², con velocidad constante v₀, el tiempo que tarda en desplazarse es

$t_{p} = \frac{x_{0} - x_{d}}{v_{0}} = \frac{2 g (μ_{s} - μ_{k})}{v_{0} ω^{2}}$

La caja está en reposo sobre la cinta, en equilibrio bajo la acción de la fuerza que ejerce el muelle kx y la fuerza de rozamiento f_r=kx del mismo módulo y de sentido contrario a la fuerza que ejerce el muelle.

En la posición x₀, la fuerza de rozamiento alcanza su valor máximo f_r= μ_s·mg y la caja comienza un nuevo ciclo.

Resumen

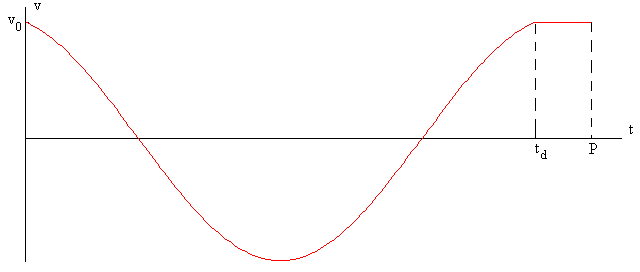
La caja describe un MAS de frecuencia angular ω centrado en la posición de equilibrio x_e= μ_k·g/ω² en la que se igualan la fuerza que ejerce el muelle y la fuerza de rozamiento, en la etapa de deslizamiento.

La amplitud del MAS es

$A = \frac{\sqrt{v_{0}^{2} ω^{2} + {(μ_{s} - μ_{k})}^{2} g^{2}}}{ω^{2}}$

salvo en la región comprendida entre x_d y x₀ o entre el instante t_d y P=t_d+t_p.

En la figura, se muestra la representación gráfica de la velocidad v de la caja en función del tiempo. Se ha señalado el tiempo t_d que emplea la caja en deslizar sobre la cinta describiendo un MAS, P es el periodo. Durante un breve intervalo de tiempo t_p=P-t_d, la caja está en reposo sobre la cinta que se mueve con velocidad constante v₀.

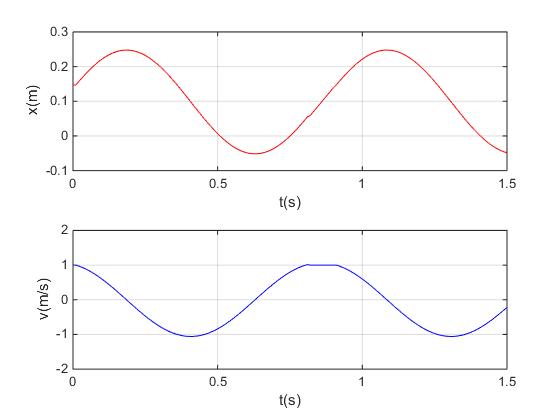
Elaboramos un script de MATLAB para representar la posición y velocidad del bloque en función del tiempo

%parámetros
vCinta=1; %velocidad de la cinta
 muEst=0.75; %coeficiente de rozamiento estático
 muDin=0.5;  %coeficiente de rozamiento cinético
fAngular=sqrt(50);   %constante del muelle 50 N/M
t=0.0;  %tiempo parcial
tipo=1;  %situación
xIniBloque=muEst*9.8/fAngular^2; %posición inicial del bloque
dt=0.01;  %intervalo de tiempo
tt=0:dt:1.5;  %tiempo total
x=zeros(1,length(tt));
v=zeros(1,length(tt));
for i=1:length(tt)  
    switch tipo
        case 1
             xBloque=xIniBloque+vCinta*t;
             vBloque=vCinta;
             if xBloque>(muEst*9.8/(fAngular*fAngular))
                t=0.0;
                xBloque=muEst*9.8/(fAngular*fAngular);
                tipo=2;
             end           
        case 2
            xBloque=vCinta*sin(fAngular*t)/fAngular+
            (muEst-muDin)*9.8*cos(fAngular*t)/(fAngular*fAngular)+
            muDin*9.8/(fAngular*fAngular);
            vBloque=vCinta*cos(fAngular*t)-
            (muEst-muDin)*9.8*sin(fAngular*t)/fAngular;
            if vBloque>vCinta
              xIniBloque=9.8*(2*muDin-muEst)/(fAngular*fAngular);
              t=0.0;
              tipo=1;
            end
    end
    x(i)=xBloque;
    v(i)=vBloque;
    t=t+dt;
end
%gráficas
subplot(2,1,1)
plot(tt,x, 'red')
grid on
xlabel('t(s)')
ylabel('x(m)')
subplot(2,1,2)
plot(tt,v,'blue')
grid on
xlabel('t(s)')
ylabel('v(m/s)')

Ejemplo

Velocidad de la cinta, v₀=1.0 m/s
Constante del muelle, k=50 N/m
Masa de la caja, m=1.0 kg
Coeficiente de rozamiento estático μ_s=0.75
Coeficiente de rozamiento cinético μ_k=0.50

La frecuencia angular del MAS es $ω = \sqrt{50} rad/s$

En el instante t=0, la caja se encuentra en la posición x₀= μ_s·g/ω²=14.7 cm

La caja describe un MAS centrado en x_e= μ_k·g/ω²=9.8 cm, de amplitud A=15.0 cm

$x = 15.0 \cdot sin (\sqrt{50} t + 0.333) + 9.8 cm$

El tiempo que la caja desliza sobre la cinta es

$t_{d} = \frac{2}{ω} (π - \arctan \frac{(μ_{s} - μ_{k}) g}{v_{0} ω}) = \frac{2}{\sqrt{50}} (π - \arctan \frac{(0.75 - 0.5) 9.8}{1.0 \cdot \sqrt{50}}) = 0.794 s$

La caja viaja sobre la cinta en reposo durante un intervalo de tiempo

$t_{p} = \frac{2 g (μ_{s} - μ_{k})}{v_{0} ω^{2}} = \frac{2 \cdot 9.8 (0.75 - 0.5)}{1.0 \cdot 50} = 0.098 s$

El tiempo total que emplea la caja en completar un ciclo es P=t_d+t_p=0.892 s

Actividades

Se introduce

El coeficiente estático, μ_s
El coeficiente cinático, μ_k
La constante elástica k del muelle, en el control titulado Constante elástica
La velocidad de la cinta v₀, en el control titulado Velocidad cinta
La masa de la caja se ha fijado en m=1.0 kg

Se debe cumplir que μ_s≥ μ_k. En el caso contrario, el programa interactivo no prosigue e invita al usuario a aumentar el coeficiente estático o a disminuir el cinético.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento de la caja.

Se representa las fuerzas sobre la caja

Una flecha de color rojo, representa la fuerza que ejerce el muelle
Una flecha de color azul, representa la fuerza de rozamiento estática.
Una flecha de color negro, representa la fuerza de rozamiento cinética

En la parte superior, se proporcionan los datos de

El tiempo
La posición de la caja
La velocidad de la caja

Constante elástica (N/m):
μ_s μ_k
Velocidad cinta (m/s):

Referencias

Denny M. Stick-slip motion: an important example of self-excited oscillation. Eur. J. Phys. 25, (2004), pp. 311-322.