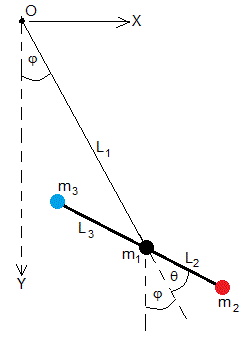
En un modelo simplificado, el cuerpo del niño se sustituye por tres masas puntuales, m₁, m₂ y m₃. La masa m₃ dista l₃ de la masa central m₁ situada en el asiento y la masa m₂ dista l₂ de dicha partícula.

• l₁ es la longitud de las cadenas que sujetan el asiento.
• φ es el ángulo que hacen las cadenas con la vertical
• θ es el ángulo que hace la línea que une las tres masas con las cadenas,

El niño oscila hacia delante y hacia atrás, sentado en el columpio, de modo que su posición angular en función del tiempo es θ=θ₀·cos(ωt). θ₀ es la amplitud y ω la frecuencia angular.

Ecuación del movimiento

Las ecuaciones de Lagrange es la forma más simple de obtener la ecuación del movimiento. Calculamos la Lagrangiana L=E_k-E_p del sistema en términos de la variable φ. E_k, es la energía cinética de las tres partículas y E_p su energía potencial. La ecuación del movimiento se obtiene.

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\dot{\phi }=\frac{d\phi }{dt}}$

Posición y velocidad de las partículas

Establecemos un sistema de referencia con el origen en el punto O, eje de sujección de las cadenas, el eje Y apuntando hacia abajo, el eje X hacia la derecha.

Posición de cada una de las tres masas

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_1=l_1\sin \phi \\ y_1=l_1\cos \phi \end{array}\\ \{\begin{array}{l}{x}_2=l_1\sin \phi +l_2\sin (\phi +\theta )\\ y_2=l_1\cos \phi +l_2\cos (\phi +\theta )\end{array}\\ \{\begin{array}{l}{x}_3=l_1\sin \phi -l_3\sin (\phi +\theta )\\ y_3=l_1\cos \phi -l_3\cos (\phi +\theta )\end{array}\end{array}}$

Derivando con respecto del tiempo, obtenemos las componentes rectangulares de las velocidades de las tres partículas

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d{x}_1}{dt}=l_1\cos \phi \frac{d\phi }{dt}\\ \frac{d{y}_1}{dt}=-l_1\sin \phi \frac{d\phi }{dt}\end{array}\\ \{\begin{array}{l}\frac{d{x}_2}{dt}=l_1\cos \phi \frac{d\phi }{dt}+l_2\cos (\phi +\theta )\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\\ \frac{d{y}_2}{dt}=-l_1\sin \phi \frac{d\phi }{dt}-l_2\sin (\phi +\theta )\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\end{array}\\ \{\begin{array}{l}\frac{d{x}_3}{dt}=l_1\cos \phi \frac{d\phi }{dt}-l_3\cos (\phi +\theta )\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\\ \frac{d{y}_3}{dt}=-l_1\sin \phi \frac{d\phi }{dt}+l_3\sin (\phi +\theta )\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\end{array}\end{array}}$

Energía cinética

Sumamos la energía cinética de las tres partículas

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}{m}_1\left({\left(\frac{d{x}_1}{dt}\right)}^2+{\left(\frac{d{y}_1}{dt}\right)}^2\right)+\frac{1}{2}{m}_2\left({\left(\frac{d{x}_2}{dt}\right)}^2+{\left(\frac{d{y}_2}{dt}\right)}^2\right)+\frac{1}{2}{m}_3\left({\left(\frac{d{x}_3}{dt}\right)}^2+{\left(\frac{d{y}_3}{dt}\right)}^2\right)\\ =\frac{1}{2}\left(m_1+m_2+m_3\right)l_1^2{\left(\frac{d\phi }{dt}\right)}^2+\frac{1}{2}\left(m_2{l}_2^2+m_3{l}_3^2\right){\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)}^2\\ -l_1\left(m_3{l}_3-m_2{l}_2\right)\cos \theta \left(\frac{d\phi }{dt}\right)\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\end{array}}$

Energía potencial

Establecemos el nivel cero en el punto de suspensión O del columpio

${\displaystyle \begin{array}{l}{E}_p=-m_{1}g{y}_1-m_{2}g{y}_2-m_{3}g{y}_3=\\ -(m_1+m_2+m_3)g{l}_1\cos \phi +(m_3{l}_3-m_2{l}_2)g\cos (\phi +\theta )\end{array}}$

Ecuación del movimiento

Calculamos las derivadas de la Lagrangiana L=E_k-E_p respecto de la velocidad angular dφ/dt y al ángulo φ

${\displaystyle \begin{array}{l}\frac{\partial L}{\partial \dot{\phi }}=(m_1+m_2+m_3)l_1^2\left(\frac{d\phi }{dt}\right)+\left(m_2{l}_2^2+m_3{l}_3^2\right)\left(\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\\ -l_1\left(m_3{l}_3-m_2{l}_2\right)\cos \theta \left(2\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)=(m_1+m_2+m_3)l_1^2\left(\frac{d^2\phi }{d{t}^2}\right)+\left(m_2{l}_2^2+m_3{l}_3^2\right)\left(\frac{d^2\phi }{d{t}^2}+\frac{d^2\theta }{d{t}^2}\right)\\ -l_1\left(m_3{l}_3-m_2{l}_2\right)\cos \theta \left(2\frac{d^2\phi }{d{t}^2}+\frac{d^2\theta }{d{t}^2}\right)+l_1\left(m_3{l}_3-m_2{l}_2\right)\sin \theta \left(2\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\left(\frac{d\theta }{dt}\right)\\ \frac{\partial L}{\partial \phi }=-(m_1+m_2+m_3)g{l}_1\sin \phi +\left(m_3{l}_3-m_2{l}_2\right)g\sin (\phi +\theta )\end{array}}$

Agrupando términos, la ecuación diferencial se escribe

${\displaystyle \begin{array}{l}{I}_1\left(\frac{d^2\phi }{d{t}^2}\right)+I_2\left(\frac{d^2\phi }{d{t}^2}+\frac{d^2\theta }{d{t}^2}\right)-l_{1}N\left(\cos \theta \left(2\frac{d^2\phi }{d{t}^2}+\frac{d^2\theta }{d{t}^2}\right)-\sin \theta \left(2\frac{d\phi }{dt}+\frac{d\theta }{dt}\right)\frac{d\theta }{dt}\right)\\ +Mg{l}_1\sin \phi -Ng\sin (\phi +\theta )=0\end{array}}$

Donde

${\displaystyle \begin{array}{l}M=m_1+m_2+m_3\\ I_1=M{l}_1^2\\ I_2=m_2{l}_2^2+m_3{l}_3^2\\ N=m_3{l}_3-m_2{l}_2\end{array}}$

El niño oscila hacia delante y hacia atrás, sentado en el columpio, de modo que su posición angular en función del tiempo es θ=θ₀·cos(ωt)

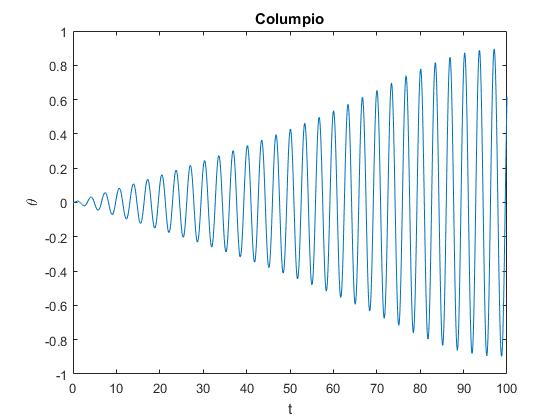
Se resuelve la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, φ=0, dφ/dt=0.

m1 = 40; %masa central
m2 = 40; %masa derecha
m3 = 20; %masa izquierda
L1 = 2.5; %longitud del péndulo
L2 = 0.4; %distancia entre m1 y m2
L3 = 0.4; %distancia entre m1 y m3
th0 = 0.7; %amplitud de la oscilación
w=1.9; %frecuencia angular 

I1=(m1+m2+m3)*L1^2; 
I2=m2*L2^2+m3*L3^2; 
N=m3*L3-m2*L2;
I0=I1+I2-2*L1*N;

datos=[(m1+m2+m3), L1, I2, N, I0, th0, w];
x0=[0,0];
[t,x]=ode45(@ed_swing,[0,100],x0,[],datos);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Columpio')

function fg=ed_swing(t,x,p)    
   M=p(1);
   L1=p(2);
   I2=p(3);
   N=p(4);
   I0=p(5);
   th0=p(6);
   w=p(7);
    
   theta=th0*cos(w*t);
   d_theta=-w*th0*sin(w*t);  %derivada
   A=-2*L1*sin(theta)*N*d_theta/I0;
   B=(N*9.8*sin(theta+x(1))-M*9.8*L1*sin(x(1)))/I0;
   C=((I2-L1*N*cos(theta))*w*w*theta-L1*N*sin(theta)*d_theta*d_theta)/I0;
   fg=[x(2); A*x(2)+B+C]; 
end 

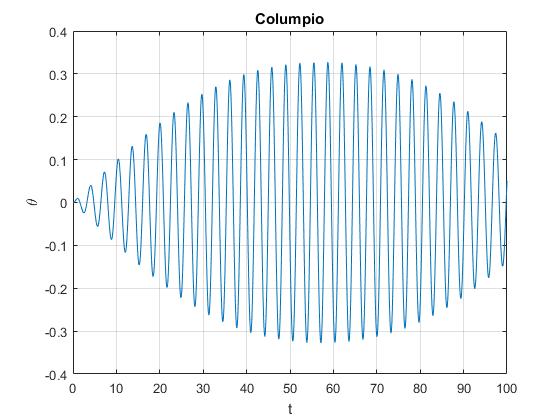
Los mismos datos, cambiando la frecuencia angular por la de un péndulo simple de longitud l₁=2.5 (longitud de las cadenas que sujetan el asiento), ω=1.98

m1 = 40; %masa central
m2 = 40; %masa derecha
m3 = 20; %masa izquierda
L1 = 2.5; %longitud del péndulo
L2 = 0.4; %distancia entre m1 y m2
L3 = 0.4; %distancia entre m1 y m3
th0 = 0.7; %amplitud de la oscilación
w=sqrt(9.8/L1); %frecuencia angular 
......

Caso particular

Si se eligen adecuadamente las masas m₂ y m₃ y las distancias l₂ y l₃ de modo m₂·l₂=m₃·l₃, es decir, que el coeficiente N sea nulo, la ecuación diferencial se reduce significativamente

${\displaystyle \left(I_1+I_2\right)\left(\frac{d^2\phi }{d{t}^2}\right)+Mg{l}_1\sin \phi =I_2{\omega }^2{\theta }_0\cos (\omega t)}$

Para oscilaciones de pequeña amplitud, hacemos la aproximación sinφ≈φ

${\displaystyle \frac{d^2\phi }{d{t}^2}+{\omega }_0^2\phi =F_0\cos (\omega t){\omega }_0^2=\frac{Mg{l}_1}{I_1+I_2}{F}_0=\frac{I_2{\omega }^2{\theta }_0}{I_1+I_2}}$

Se trata de un oscilador de frecuencia propia ω₀ bajo la acción de una fuerza oscilante de amplitud F₀ y frecuencia ω.

La solución particular de esta ecuación diferencial es de la forma C·cos(ωt). Calculamos el coeficiente C

${\displaystyle C=\frac{F_0}{{\omega }_0^2-{\omega }^2}}$

La solución de la homogénea tiene la forma A·sin(ω₀t)+B·cos(ω₀t)

La solución general es de la forma θ= Asin(ω₀t)+Bcos(ω₀t)+Ccos(ωt). Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, θ=0, dθ/dt=0

${\displaystyle \theta =\frac{F_0}{{\omega }_0^2-{\omega }^2}\left(\cos (\omega t)-\cos ({\omega }_{0}t)\right)=\frac{2F_0}{{\omega }_0^2-{\omega }^2}\sin \left(\frac{{\omega }_0+\omega }{2}t\right)\sin \left(\frac{{\omega }_0-\omega }{2}t\right)}$

Consideremos la situación en la que la frecuencia de la fuerza oscilante se hace próxima a la frecuencia propia del oscilador ω≈ω₀. Utilizando el resultado, sinx/x tiende hacia 1 cuando x tiende a cero

${\displaystyle \theta =\frac{F_{0}t}{2{\omega }_0}\sin \left({\omega }_{0}t\right)}$

La amplitud de la oscilación crece linealmente con el tiempo t

En la figura se muestra el resultado para los siguientes datos:

m1 = 40; %masa central
m2 = 40; %masa derecha
m3 = 20; %masa izquierda
L1 = 2.5; %longitud del péndulo
L2 = 0.4; %distancia entre m1 y m2
L3 = 0.8; %distancia entre m1 y m3
th0 = 0.7; %amplitud de la oscilación
w=1.905; %frecuencia angular 
.....

Se cumple que m₂·l₂=m₃·l₃

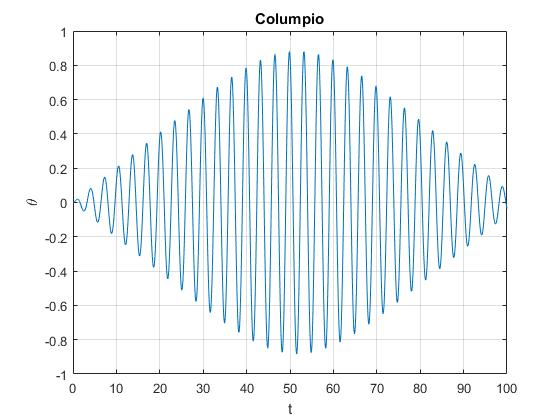
La amplitud va creciendo linealmente al principio. Luego, la amplitud se hace grande y la aproximación sinφ≈φ deja de tener validez

Actividades

Se introduce

• La frecuencia angular ω, en el control titulado Frecuencia angular
• La masa central m₁, en el control titulado m₁
• La masa m₂, en el control titulado m₂
• La masa m₃, en el control titulado m₃
• La distancia l₂, en el control titulado l₂
• La distancia l₃, en el control titulado l₃
• La distancia l₁, la longitud de las cadenas que sujetan al asiento se ha fijado en 2.5
• La amplitud de la oscilación del niño θ₀ sobre el asiento se ha fijado en 0.7 rad, 40°

Se pulsa el botón titulado Nuevo

Si se activa la casilla titulada Gráfica y se pulsa el botón titulado Nuevo, se verá la representación gráfica del ángulo φ que hace el columpio con la vertical en función del tiempo t. Para ver de nuevo el columpio en movimiento de desactiva esta casilla y se pulsa el botón titulado Nuevo.

Fijadas las masas m₁, m₂ y m₃ y las distancias l₁, l₂ y l₃, se tratará de investigar a qué frecuencias ω se obtiene una amplitud de φ grande.

Referencias

William B. Case, Mark A. Swanson. The pumping of a swing from the seated position. Am. J. Phys. 58 (5) May 1990, pp. 463-467

Johnathon Jackson. Analysis of The Motion of Pumping on A Swing, May 2004. http://msemac.redwoods.edu/~darnold/math55/deproj/sp04/jjackson/paperIIII.pdf