Oscilaciones amortiguadas

Estudiamos la ecuación diferencial de segundo orden que describe el oscilador amortiguado, con las condiciones iniciales especificadas: en el instante t=0, la posición es es x₀ y la velocidad es v₀.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0\\ t=0\{\begin{array}{l}x=x_0\\ \frac{dx}{dt}=v_0\end{array}\end{array}}$

• ω₀ es la frecuencia natural o propia del oscilador
• γ es la constante de amortiguamiento, γ<ω₀

La transformada de Laplace de la ecuación diferencial es

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0\\ t=0\{\begin{array}{l}x=x_0\\ \frac{dx}{dt}=v_0\end{array}\\ \left(s^{2}F(s)-s·x(0)-x\text{'}(0)\right)+2\gamma \left(sF(s)-x(0)\right)+{\omega }_0^{2}F(s)=0\\ \left(s^{2}F(s)-s·x_0-v_0\right)+2\gamma \left(sF(s)-x_0\right)+{\omega }_0^{2}F(s)=0\\ F(s)=\frac{s{x}_0+2\gamma x_0+v_0}{\left(s^2+2\gamma s+{\omega }_0^2\right)}\end{array}}$

Escribimos F(s) de modo que se pueda aplicar transformada inversa de Laplace, ilaplace mirando directamente a la tabla de transformadas .

${\displaystyle \begin{array}{l}F(s)=\frac{x_0(s+\gamma )}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}+\frac{\left(\gamma x_0+v_0\right)}{\sqrt{{\omega }_0^2-{\gamma }^2}}\frac{\sqrt{{\omega }_0^2-{\gamma }^2}}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\\ x=x_0{e}^{-\gamma t}\cos (\omega t)+\frac{\left(\gamma x_0+v_0\right)}{\omega }{e}^{-\gamma t}\sin (\omega t)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

Que es la misma solución que ya hemos obtenido anteriormente

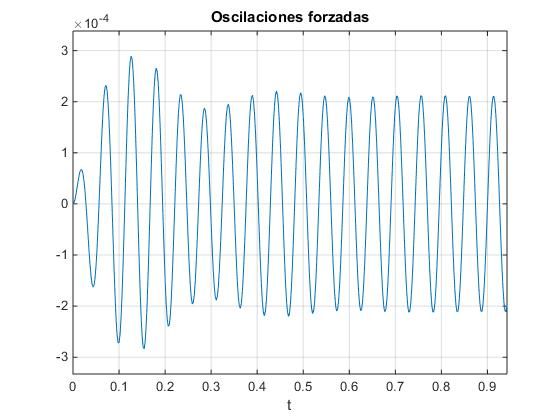
Calculamos la transformada inversa de Laplace con MATLAB y representamos la solución de la ecuación diferencial para ω₀=100 rad/s, γ=7s^-1, y las condiciones iniciales x₀=5 y v₀=0.

>> clear
>> syms g w0 s x0 v0;
>> Fs=(s*x0+2*g*x0+v0)/(s^2+2*g*s+w0^2);
>> x=ilaplace(Fs);
>> xx=subs(x,{g w0 x0 v0},{7 100 5 0});
>> ezplot(xx,[0 0.3*pi])
>> ylim([-5 5])
>> grid on
>> title('oscilaciones amortiguadas')

Oscilaciones forzadas

Estudiamos la ecuación diferencial de segundo orden que describe el oscilador forzado, con las condiciones iniciales especificadas.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{F}{m}\cos ({\omega }_{f}t)\\ t=0\{\begin{array}{l}x=0\\ \frac{dx}{dt}=0\end{array}\end{array}}$

• donde ω₀ es la frecuencia natural o propia del oscilador
• ω_f es la frecuencia angular de la fuerza oscilante de amplitud F
• γ es la constante de amortiguamiento,  γ<ω₀

Supondremos que la amplitud de la fuerza oscilante F/m=1 y que ω₀≠ω_f .

La transformada de Laplace de la ecuación diferencial es

${\displaystyle \begin{array}{l}\left(s^{2}F(s)-s·x(0)-x\text{'}(0)\right)+2\gamma \left(sF(s)-x(0)\right)+{\omega }_0^{2}F(s)=\frac{s}{s^2+{\omega }_f^2}\\ F(s)=\frac{s}{\left(s^2+{\omega }_f^2\right)\left(s^2+2\gamma s+{\omega }_0^2\right)}\end{array}}$

Escribimos F(s) como suma de fracciones más simples.

${\displaystyle \begin{array}{l}F(s)=\frac{s}{\left(s^2+{\omega }_f^2\right)\left({(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)\right)}=\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\\ \{\begin{array}{l}A+C=0\\ 2\gamma A+B+D=0\\ {\omega }_0^{2}A+2\gamma D+{\omega }_f^{2}C=1\\ {\omega }_0^{2}B+{\omega }_f^{2}D=0\end{array}\\ A=\frac{{\omega }_0^2-{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}B=\frac{2\gamma {\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\\ C=-\frac{{\omega }_0^2-{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}D=-\frac{2\gamma {\omega }_0^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\end{array}}$

Utilizamos MATLAB para resolver el sistema de cuatro ecuaciones con cuatro incógnitas. En el código MATLAB llamamos

• Coeficiente de rozamiento, γ (g),
• Frecuencia angular propia, ω₀ (w0),
• Frecuencia angular de la fuerza oscilante, ω_f (wf)

>> syms g w0 wf s;
>> A=[1 0 1 0; 2*g 1 0 1; w0^2 2*g wf^2 0; 0 w0^2 0 wf^2];
>> b=sym('[0;0;1;0]');
>> X=A\b
X =
  (w0^2 - wf^2)/(4*g^2*wf^2 + w0^4 - 2*w0^2*wf^2 + wf^4)
     (2*g*wf^2)/(4*g^2*wf^2 + w0^4 - 2*w0^2*wf^2 + wf^4)
 -(w0^2 - wf^2)/(4*g^2*wf^2 + w0^4 - 2*w0^2*wf^2 + wf^4)
    -(2*g*w0^2)/(4*g^2*wf^2 + w0^4 - 2*w0^2*wf^2 + wf^4)

Escribimos F(s) de modo que se pueda aplicar la transformada inversa de Laplace mirando directamente a la tabla de transformadas .

${\displaystyle \begin{array}{l}F(s)=A\frac{s}{s^2+{\omega }_f^2}+\frac{B}{{\omega }_f}\frac{1}{s^2+{\omega }_f^2}+\frac{\left(s+\gamma \right)}{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}+\\ \frac{D-C\gamma }{\sqrt{{\omega }_0^2-{\gamma }^2}}\frac{\sqrt{{\omega }_0^2-{\gamma }^2}}{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}\\ x=A\cos \left({\omega }_{f}t\right)+\frac{B}{{\omega }_f}\sin \left({\omega }_{f}t\right)+C{e}^{-\gamma t}\cos \left(\omega t\right)+\frac{D-C\gamma }{\omega }{e}^{-\gamma t}\sin \left(\omega t\right)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

Los dos primeros términos describen el estado estacionario y los dos últimos el estado transitorio que desaparece al cabo de un tiempo teóricamente infinito al estar multiplicados por exp(-γt).

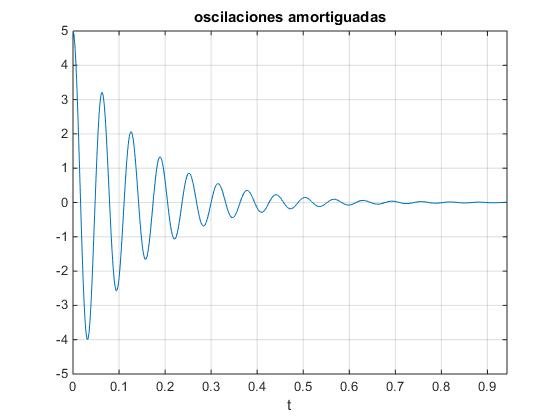
Calculamos la transformada inversa de Laplace con MATLAB y representamos la solución x de la ecuación diferencial para los valores γ=7, ω₀=100 y ω_f=120 y las condiciones iniciales x₀=0 y v₀=0.

>> syms g w0 wf s;
>> Fs=s/((s^2+wf^2)*(s^2+2*g*s+w0^2));
>> x=ilaplace(Fs);
>> xx=subs(x,{g w0 wf},{7 100 120});
>> ezplot(xx,[0 0.3*pi])