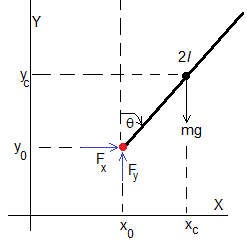
Sea una varilla de masa m y de longitud 2l. Las coordendas del centro de suspensión son (x₀, y₀). Cuando el ángulo que forma la varilla con la vertical es θ, las coordenadas de su centro de masas son x_c=x₀+lsinθ, y_c=y₀+lcosθ

Sobre el péndulo actúan las siguientes fuerzas:

• Una fuerza horizontal F_x en el centro de suspensión

• Una fuerza vertical F_y aplicada en el centro de suspensión y el peso mg en el centro de masas

Aplicamos la segunda ley de Newton a los movimientos de traslación del centro de masas a lo largo del eje X y del eje Y

${\displaystyle \begin{array}{l}m\frac{d^2{x}_c}{d{t}^2}=F_x\\ m\frac{d^2{y}_c}{d{t}^2}=F_y-mg\end{array}}$

Aplicamos la ecuación de la dinámica de rotación alrededor de un eje perpendicular a la varilla y que pasa por el centro de masas. Se ha de tener en cuenta que los ángulos positivos se miden en el sentido de las agujas del reloj. El momento de F_y es positivo y el de F_x es negativo.

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=F_{y}l\sin \theta -F_{x}l\cos \theta }$

El momento de inercia de una varilla de longitud 2l es I_c=ml²/3. La ecuación de la dinámica de rotación se expresa de forma alternativa

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=ml\left(\frac{d^2{y}_c}{d{t}^2}+g\right)\sin \theta -ml\frac{d^2{x}_c}{d{t}^2}\cos \theta }$

De la relación entre las coordenadas del centro de masa con las del centro de suspensión y el desplazamiento angular del péndulo, tenemos

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_c=x_0+l\sin \theta \\ y_c=y_0+l\cos \theta \end{array}\\ \{\begin{array}{l}\frac{d{x}_c}{dt}=\frac{d{x}_0}{dt}+l\cos \theta \frac{d\theta }{dt}\\ \frac{d{y}_c}{dt}=\frac{d{y}_0}{dt}-l\sin \theta \frac{d\theta }{dt}\end{array}\\ \{\begin{array}{l}\frac{d^2{x}_c}{d{t}^2}=\frac{d^2{x}_0}{d{t}^2}+l\cos \theta \frac{d^2\theta }{d{t}^2}-l\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\\ \frac{d^2{y}_c}{d{t}^2}=\frac{d^2{y}_0}{d{t}^2}-l\sin \theta \frac{d^2\theta }{d{t}^2}-l\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\end{array}\end{array}}$

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=ml\left(\frac{d^2{y}_0}{d{t}^2}-l\sin \theta \frac{d^2\theta }{d{t}^2}-l\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+g\right)\sin \theta -ml\left(\frac{d^2{x}_0}{d{t}^2}+l\cos \theta \frac{d^2\theta }{d{t}^2}-l\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\cos \theta \\ \frac{I_c+m{l}^2}{ml}\frac{d^2\theta }{d{t}^2}+\frac{d^2{x}_0}{d{t}^2}\cos \theta -\left(\frac{d^2{y}_0}{d{t}^2}+g\right)\sin \theta =0\end{array}}$

Estudiamos ahora las tres situaciones

• El centro de suspensión vibra verticalmente

x₀=0, y₀=Acos(ωt)

${\displaystyle \frac{I_c+m{l}^2}{ml}\frac{d^2\theta }{d{t}^2}+\left(A{\omega }^2\cos (\omega t)-g\right)\sin \theta =0}$

• El centro de suspensión vibra horizontalmente

y₀=0, x₀=Acos(ωt)

${\displaystyle \frac{I_c+m{l}^2}{ml}\frac{d^2\theta }{d{t}^2}-A{\omega }^2\cos (\omega t)\cos \theta -g\sin \theta =0}$

• El centro de suspensión se mueve en una circunferencia de radio A con velocidad angular ω

x₀=Acos(ωt), y₀=Asin(ωt)

${\displaystyle \begin{array}{l}\frac{I_c+m{l}^2}{ml}\frac{d^2\theta }{d{t}^2}-A{\omega }^2\cos (\omega t)\cos \theta +\left(A{\omega }^2\sin (\omega t)-g\right)\sin \theta =0\\ \frac{I_c+m{l}^2}{ml}\frac{d^2\theta }{d{t}^2}-A{\omega }^2\cos (\theta -\omega t)-g\sin \theta =0\end{array}}$

El centro de suspensión vibra horizontalmente

Consideraremos dos casos:

• El péndulo en posición casi invertida, el centro de masas por encima del de suspensión



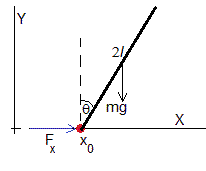
En la aproximación de oscilaciones de pequeña amplitud, sinθ≈θ, cosθ≈1, la ecuación del movimiento se escribe

${\displaystyle \frac{d^2\theta }{d{t}^2}-{\omega }_0^2\theta =D\cos (\omega t)\{\begin{array}{l}{\omega }_0^2=\frac{ml}{I_c+m{l}^2}g\\ D=\frac{ml}{I_c+m{l}^2}A{\omega }^2\end{array}}$

La solución de la ecuación diferencial homogénea es

${\displaystyle \theta =a\exp ({\omega }_{0}t)+b\exp (-{\omega }_{0}t)}$

La solución particular es

${\displaystyle {\theta }_1=E\cos (\omega t),\omega \ne {\omega }_0}$

La introducimos en la ecuación diferencial para determinar el coeficiente E

${\displaystyle \begin{array}{l}-{\omega }^{2}E\cos (\omega t)-{\omega }_0^{2}E\cos (\omega t)=D\cos (\omega t)\\ E=-\frac{D}{{\omega }^2+{\omega }_0^2}\end{array}}$

La solución completa es la suma de la homogénea y de la particular

${\displaystyle \begin{array}{l}\theta =a\exp ({\omega }_{0}t)+b\exp (-{\omega }_{0}t)-\frac{D}{{\omega }^2+{\omega }_0^2}\cos (\omega t),\omega \ne {\omega }_0\\ \frac{d\theta }{dt}=a{\omega }_0\exp ({\omega }_{0}t)-b{\omega }_0\exp (-{\omega }_{0}t)+\frac{\omega D}{{\omega }^2+{\omega }_0^2}\sin (\omega t)\end{array}}$

Los coeficientes a y b se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}a=\frac{1}{2}\left({\theta }_0+\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0+\frac{D}{{\omega }^2+{\omega }_0^2}\right)\\ b=\frac{1}{2}\left({\theta }_0-\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0+\frac{D}{{\omega }^2+{\omega }_0^2}\right)\end{array}}$

Para que las oscilaciones no crezcan exponencialmente con el tiempo, el coeficiente a deberá ser nulo, lo que implica que

${\displaystyle \begin{array}{l}{\theta }_0+\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0+\frac{D}{{\omega }^2+{\omega }_0^2}=0\\ b=-\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0\end{array}}$

Con esta relación entre las condiciones iniciales, el desplazamiento angular θ del péndulo con el tiempo t es

${\displaystyle \theta =-\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0\exp (-{\omega }_{0}t)-\frac{D}{{\omega }^2+{\omega }_0^2}\cos (\omega t)}$

Al cabo de un cierto tiempo, el estado transitorio desaparece, la exponencial tiende a cero. El estado estacionario se caracteriza por la oscilación

${\displaystyle {\theta }_{\infty }=-\frac{D}{{\omega }^2+{\omega }_0^2}\cos (\omega t)}$

• El péndulo en posición normal, el centro de masas por debajo del centro de suspensión

En este caso, el ángulo φ=π-θ.

${\displaystyle \begin{array}{l}-\frac{I_c+m{l}^2}{ml}\frac{d^2\phi }{d{t}^2}-A{\omega }^2\cos (\omega t)\cos (\pi -\phi )-g\sin (\pi -\phi )=0\\ \frac{I_c+m{l}^2}{ml}\frac{d^2\phi }{d{t}^2}-A{\omega }^2\cos (\omega t)\cos \phi +g\sin \phi =0\end{array}}$



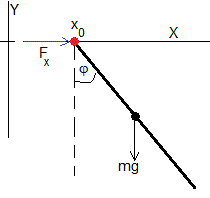
La ecuación del movimiento para las oscilaciones de pequeña amplitud sinφ≈θ, cosφ≈1

${\displaystyle \frac{d^2\phi }{d{t}^2}+{\omega }_0^2\phi =D\cos (\omega t)\{\begin{array}{l}{\omega }_0^2=\frac{ml}{I_c+m{l}^2}g\\ D=\frac{ml}{I_c+m{l}^2}A{\omega }^2\end{array}}$

La solución de la ecuación diferencial homogénea es

${\displaystyle \phi =a\exp (i{\omega }_{0}t)+b\exp (-i{\omega }_{0}t)}$

La solución particular es

${\displaystyle {\phi }_1=E\cos (\omega t)}$

La introducimos en la ecuación diferencial para determinar el coeficiente E

${\displaystyle \begin{array}{l}-{\omega }^{2}E\cos (\omega t)+{\omega }_0^{2}E\cos (\omega t)=D\cos (\omega t)\\ E=-\frac{D}{{\omega }^2-{\omega }_0^2}\end{array}}$

La solución completa es la suma de la homogénea y de la particular

${\displaystyle \begin{array}{l}\phi =a\exp (i{\omega }_{0}t)+b\exp (-i{\omega }_{0}t)-\frac{D}{{\omega }^2-{\omega }_0^2}\cos (\omega t)\\ \frac{d\phi }{dt}=ai{\omega }_0\exp (i{\omega }_{0}t)-bi{\omega }_0\exp (-i{\omega }_{0}t)+\frac{\omega D}{{\omega }^2-{\omega }_0^2}\sin (\omega t)\end{array}}$

Los coeficientes a y b se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}a=\frac{1}{2}\left({\phi }_0+\frac{D}{{\omega }^2+{\omega }_0^2}+\frac{1}{i{\omega }_0}{\left(\frac{d\phi }{dt}\right)}_0\right)\\ b=\frac{1}{2}\left({\phi }_0+\frac{D}{{\omega }^2+{\omega }_0^2}-\frac{1}{i{\omega }_0}{\left(\frac{d\phi }{dt}\right)}_0\right)\end{array}}$

El desplazamiento angular φ del péndulo con el tiempo t es

${\displaystyle \phi =\left({\phi }_0+\frac{D}{{\omega }^2+{\omega }_0^2}\right)\cos ({\omega }_{0}t)+\frac{1}{{\omega }_0}{\left(\frac{d\theta }{dt}\right)}_0\sin ({\omega }_{0}t)-\frac{D}{{\omega }^2-{\omega }_0^2}\cos (\omega t)}$

Es la combinación lineal de dos movimientos armónicos de frecuencias ω y ω₀.

Cuando ω se hace próxima a ω₀ el último término crece y el sistema se vuelve inestable

Equilibrio y estabilidad

La ecuación del movimiento de una partícula de masa m unida a un muelle elástico de constante k es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-kx}$

La fuerza -kx es la derivada de la energía potencial E_p(x)=kx²/2 cambiada de signo

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-\frac{d{E}_p(x)}{dx}}$

Para un péndulo simple, una partícula de masa m unida a una varilla rígida de longitud l y masa despreciable, la ecuación del movimiento es

${\displaystyle m{l}^2\frac{d^2\theta }{d{t}^2}=-mgl\sin \theta }$

La energía potencial es E_p(θ)=-mglcosθ.

${\displaystyle m{l}^2\frac{d^2\theta }{d{t}^2}=-\frac{d{E}_p(\theta )}{d\theta }}$

Consideremos el movimiento de una partícula sometida a la acción simultánea de un campo, independiente del tiempo, de energía potencial E_p(x) y de una fuerza que depende de la posición x y del tiempo t de la forma, f(x,t)=f₁(x)·sin(ωt)+f₂(x)·cos(ωt)

La fuerza f(x,t) varía con el tiempo con una frecuencia elevada ω. Se entiende frecuencia elevada una frecuencia ω>>ω₀, donde ω₀ es la frecuencia natural del movimiento de la partícula bajo la acción únicamente de la fuerza descrita por la energía potencial E_p(x). La ecuación del movimiento de la partícula es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-\frac{d{E}_p(x)}{dx}+f(x,t)}$

La partícula se moverá a lo largo de la trayectoria descrita por el campo y realizará pequeñas oscilaciones de frecuencia ω alrededor de esta trayectoria. Por tanto, la solución de esta ecuación diferencial es la suma de dos términos

${\displaystyle x(t)=X(t)+\xi (t)}$

donde ξ(t) corresponde a estas pequeñas oscilaciones. El resultado final, es que la partícula se mueve en un potencial efectivo. Véase el libro Mecánica de Landau

${\displaystyle U(x)=E_p(x)+\frac{f_1^2+f_2^2}{4m{\omega }^2}}$

El centro de suspensión vibra horizontalmente

Consideremos una partícula de masa m unida a una varilla rígida de longitud l y masa despreciable. El momento de inercia respecto del eje que pasa por el centro de suspensión es I_c+ml²=ml². La ecuación del movimiento

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{g}{l}\sin \theta +\left(A\frac{{\omega }^2}{l}\cos \theta \right)\cos (\omega t)}$

El primer término es la derivada cambiada de signo de la función e_p(θ)=(g/l)cosθ

${\displaystyle \frac{g}{l}\sin \theta =-\frac{du(\theta )}{d\theta }}$

El potencial efectivo es

${\displaystyle u(\theta )=\frac{g}{l}\cos \theta +\frac{{\left(A\frac{{\omega }^2}{l}\cos \theta \right)}^2}{4{\omega }^2}=\frac{g}{l}\left(\cos \theta +k{\cos }^2\theta \right),k=\frac{A^2{\omega }^2}{4gl}}$

Para determinar las posiciones θ de equilibrio (estable o inestable), calculamos la derivada

${\displaystyle -\sin \theta -2k\sin \theta \cos \theta =\mathrm{0,}\{\begin{array}{l}\theta =\mathrm{0,}\pi \\ \cos \theta =-\frac{1}{2k},k>\frac{1}{2}\end{array}}$

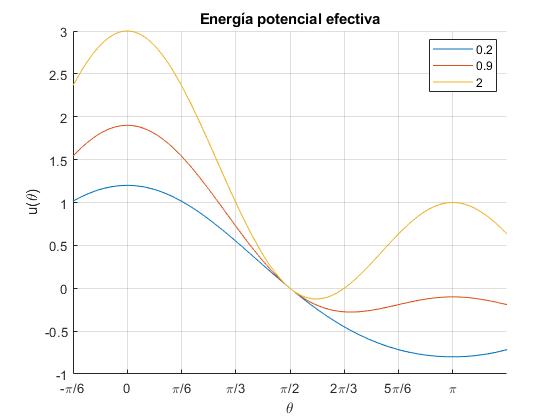
La energía potencial efectiva es una curva simétrica, por lo que representamos la función u(θ) para tres valores del parámetro k=0.2,0.9 y 2, en el intervalo -30°<θ<210°

hold on
for k=[0.2,0.9,2]
    f=@(x) cos(x)+k*cos(x).^2;
    fplot(f,[-pi/6,pi+pi/6],'displayName',num2str(k))
end
hold off
grid on
xlabel('\theta')
legend('-DynamicLegend','location','best')
set(gca,'XTick',-pi/6:pi/6:pi)
set(gca,'XTickLabel',{'-\pi/6','0','\pi/6','\pi/3','\pi/2','2\pi/3',
'5\pi/6','\pi'})
ylabel('u(\theta)')
xlim([-pi/6,pi+pi/6])
title('Energía potencial efectiva')

Estabilidad

Para k<1/2, la posición de equilibrio estable es θ=π. Para k>1/2, la posición de equilibrio estable es θ=arcos(-1/2·k). La posición θ=0 es de equilibrio inestable

Examinamos el signo de la derivada segunda de u(θ)

• positivo, mínimo, equilibrio estable
• negativo, máximo, equilibrio inestable

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{\theta }^2}=-\cos \theta -2k\left({\cos }^2\theta -{\sin }^2\theta \right)=-\cos \theta -2k\left(2{\cos }^2\theta -1\right)\\ \{\begin{array}{l}\mathrm{0,}-1-2k<0\\ \pi ,1-2k\{\begin{array}{l}<\mathrm{0,}k>\frac{1}{2}\\ >\mathrm{0,}k<\frac{1}{2}\end{array}\\ \cos \theta =-\frac{1}{2k},k>\frac{1}{2},2k-\frac{1}{2k}>0\end{array}\end{array}}$

El centro de suspensión vibra verticalmente

La ecuación del movimiento es

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{g}{l}\sin \theta -\left(A\frac{{\omega }^2}{l}\sin \theta \right)\cos (\omega t)}$

El potencial efectivo es

${\displaystyle u(\theta )=\frac{g}{l}\cos \theta +\frac{{\left(-A\frac{{\omega }^2}{l}\sin \theta \right)}^2}{4{\omega }^2}=\frac{g}{l}\left(\cos \theta +k{\sin }^2\theta \right),k=\frac{A^2{\omega }^2}{4gl}}$

Para determinar las posiciones θ de equilibrio (estable o inestable), calculamos la derivada

${\displaystyle -\sin \theta +2k\sin \theta \cos \theta =\mathrm{0,}\{\begin{array}{l}\theta =\mathrm{0,}\pi \\ \cos \theta =\frac{1}{2k},k>\frac{1}{2}\end{array}}$

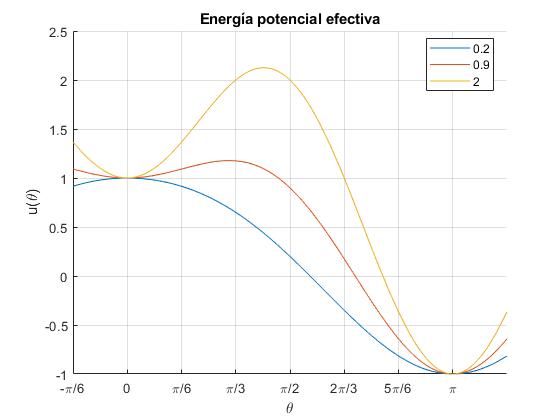
Representamos la función u(θ) para tres valores del parámetro k=0.2,0.9 y 2, en el intervalo -30°<θ<210°

hold on
for k=[0.2,0.9,2]
    f=@(x) cos(x)+k*sin(x).^2;
    fplot(f,[-pi/6,pi+pi/6],'displayName',num2str(k))
end
hold off
grid on
xlabel('\theta')
legend('-DynamicLegend','location','best')
set(gca,'XTick',-pi/6:pi/6:pi)
set(gca,'XTickLabel',{'-\pi/6','0','\pi/6','\pi/3','\pi/2','2\pi/3',
'5\pi/6','\pi'})
ylabel('u(\theta)')
xlim([-pi/6,pi+pi/6])
title('Energía potencial efectiva')

Estabilidad

La posición de equilibrio estable es θ=π. Para k>1/2, θ=0 es también posición de equilibrio estable. La posición θ=arcos(1/2·k) con k>1/2 es de equilibrio inestable

Examinamos el signo de la derivada segunda de u(θ)

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{\theta }^2}=-\cos \theta +2k\left({\cos }^2\theta -{\sin }^2\theta \right)=-\cos \theta +2k\left(2{\cos }^2\theta -1\right)\\ \{\begin{array}{l}\mathrm{0,}-1+2k\{\begin{array}{l}<\mathrm{0,}k<\frac{1}{2}\\ >\mathrm{0,}k>\frac{1}{2}\end{array}\\ \pi ,1+2k>0\\ \cos \theta =\frac{1}{2k},k>\frac{1}{2},\frac{1}{2k}-2k<0\end{array}\end{array}}$

El centro de suspensión vibra horizontalmente

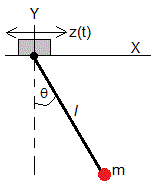
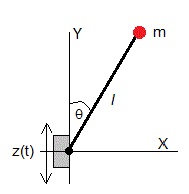
Supongamos un péndulo formado por una varilla inextensible y sin peso de longitud l, en cuyo extremo hay una partícula de masa m. El centro de suspensión describe un Movimiento Armónico Simple a lo largo del eje horizontal X con amplitud A y frecuencia angular ω, z(t)=Acos(ωt). Vamos a estudiar las oscilaciones forzadas de este sistema oscilante.

Establecemos un origen y unos ejes X e Y como se muestra en la figura. La posición de la partícula de masa m es

${\displaystyle \{\begin{array}{l}x=A\cos \left(\omega t\right)+l\sin \theta \\ y=-l\cos \theta \end{array}}$

Derivando respecto del tiempo, obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=-A\omega \sin \left(\omega t\right)+l\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\\ \frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)-2lA\omega \sin \left(\omega t\right)\cos \theta \frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}}$

La energía potencial de la masa m es mgy=-mglcosθ

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)-2lA\omega \sin \left(\omega t\right)\cos \theta \frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)+mgl\cos \theta \\ L=\frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)-2lA\omega \sin \left(\omega t\right)\cos \theta ·\dot{\theta }+l^2{\dot{\theta }}^2\right)+mgl\cos \theta \end{array}}$

Ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ l\frac{d^2\theta }{d{t}^2}+g\sin \theta -A{\omega }^2\cos \left(\omega t\right)\cos \theta =0\end{array}}$

Se obtiene la ecuación diferencial del movimiento

${\displaystyle \frac{d^2\theta }{d{t}^2}+{\omega }_0^2\sin \theta =\frac{A}{l}{\omega }^2\cos (\omega t)\cos \theta }$

Donde ${\omega }_0^2=g/l$ es la frecuencia natural de las oscilaciones del péndulo. Si además, suponemos que actúa una fuerza de rozamiento proporcional a la velocidad dθ/dt, añadimos, como en las oscilaciones amortiguadas, el término 2γ·dθ/dt

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\sin \theta =\frac{A}{l}{\omega }^2\cos (\omega t)\cos \theta }$

Resolveremos la ecuación diferencial por el procedimiento numérico ode45 con las siguientes condiciones iniciales t=0, θ=0, dθ/dt=0. Representaremos la posición angular θ del péndulo en función del tiempo t para varias frecuencias ω próximas a la de resonancia ω₀

• Longitud del péndulo, l=0.195 m
• Amplitud de la oscilación del centro de suspensión del péndulo, A= 4.5 mm
• Constante de amortiguamiento, γ=0.025 s^-1

A=0.0045; %amplitud de la oscilación del centro de suspensión
gamma=0.025; %amortiguamiento
L=0.195; %longitud del péndulo
w0=sqrt(9.8/L); %frecuencia natural

w=6.28; %frecuencia de oscilación del centro de suspensión
fg=@(t,x)[x(2);A*w^2*cos(w*t)*cos(x(1))/L-w0^2*sin(x(1))-2*gamma*x(2)];
[t,x]=ode45(fg,[0,15],[0,0]);
plot(t, x(:,1)) 
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo forzado')

>> w0
w0 =    7.0892

Frecuencias ω de oscilación del centro de suspensión

• ω=6.28 rad/s



• ω=6.91 rad/s



• ω=7.54 rad/s



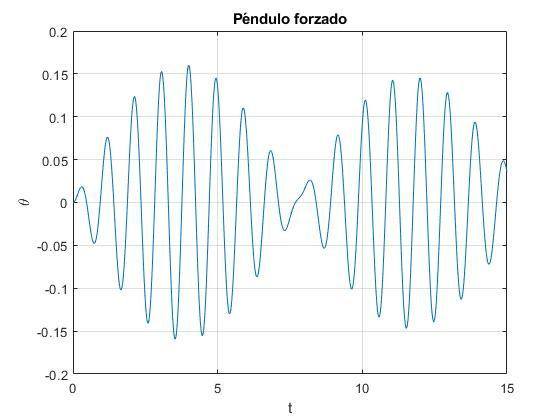
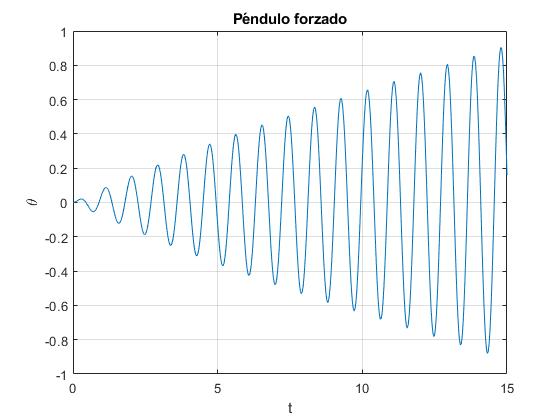
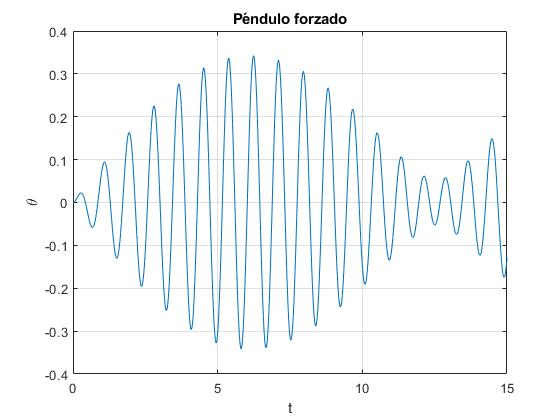
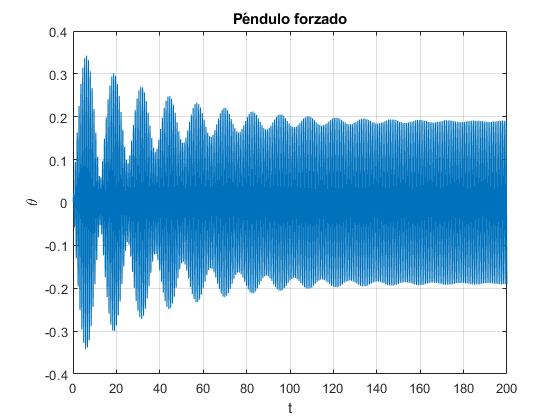
El estado estacionario, (amplitud constante) se alcanza después de un tiempo teóricamente infinito

Representamos la amplitud en el estado estacionario, en función de la frecuencia en el intervalo 5<ω<8 rad/s

A=0.0045; %amplitud de la oscilación del centro de suspensión
gamma=0.025; %amortiguamiento
L=0.195; %longitud del péndulo
w0=sqrt(9.8/L); %frecuencia natural

ww=linspace(5,8,100);
th_max=zeros(1,length(ww));
i=1;
for w=ww
    fg=@(t,x)[x(2);A*w^2*cos(w*t)*cos(x(1))/L-w0^2*sin(x(1))-2*gamma*x(2)];
    [t,x]=ode45(fg,[0,200],[0,0]);
    amp=abs(x(:,1)).*(t>190); %amplitud casi constante
    th_max(i)=max(amp);
    i=i+1;
end
plot(ww, th_max) 
grid on
xlabel('\omega')
ylabel('\theta_m')
title('Amplitud-frecuencia')

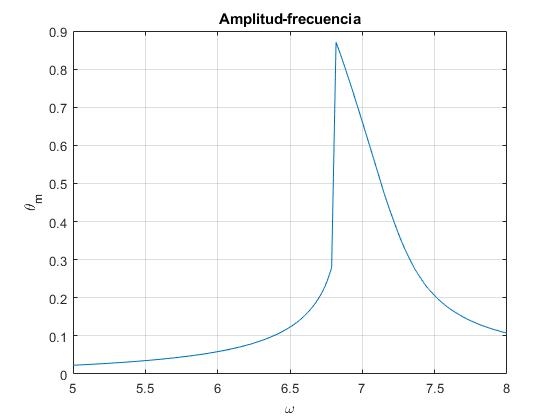
Utilizamos Data tip para medir el máximo de la amplitud que se obtiene para la frecuencia ω=6.818 rad/s

El péndulo invertido

Supongamos un péndulo formado por una varilla inextensible y sin peso de longitud l, en cuyo extremo hay una partícula de masa m. El centro de suspensión describe un Movimiento Armónico Simple a lo largo del eje vertical Y con amplitud A y frecuencia angular ω, z(t)=Acos(ωt). Vamos a estudiar las oscilaciones forzadas de este sistema oscilante.

Establecemos un origen y unos ejes X e Y como se muestra en la figura. La posición de la partícula de masa m es

${\displaystyle \{\begin{array}{l}x=l\sin \theta \\ y=A\cos \left(\omega t\right)+l\cos \theta \end{array}}$

Derivando respecto del tiempo, obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=l\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=-A\omega \sin \left(\omega t\right)-l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\\ \frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)+2lA\omega \sin \left(\omega t\right)\sin \theta \frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}}$

La energía potencial de la masa m es mgy

${\displaystyle V=mgA\cos \left(\omega t\right)+mgl\cos \theta }$

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)+2lA\omega \sin \left(\omega t\right)\sin \theta \frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)-mgA\cos \left(\omega t\right)-mgl\cos \theta \\ L=\frac{1}{2}m\left(A^2{\omega }^2{\sin }^2\left(\omega t\right)+2lA\omega \sin \left(\omega t\right)\sin \theta ·\dot{\theta }+l^2{\dot{\theta }}^2\right)-mgA\cos \left(\omega t\right)-mgl\cos \theta \end{array}}$

Ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ l\frac{d^2\theta }{d{t}^2}+\sin \theta \left(A{\omega }^2\cos \left(\omega t\right)-g\right)=0\end{array}}$

Para resolver la ecuación diferencial por procedimientos numéricos, despejamos la aceleración

${\displaystyle \frac{d^2\theta }{d{t}^2}=\left({\omega }_0^2-\frac{A}{l}{\omega }^2\cos \left(\omega t\right)\right)\sin \theta }$

Donde ${\omega }_0^2=g/l$ es la frecuencia natural de las oscilaciones del péndulo. Resolvemos la ecuación diferencial con las siguientes condiciones iniciales t=0, θ=θ₀, dθ/dt=0

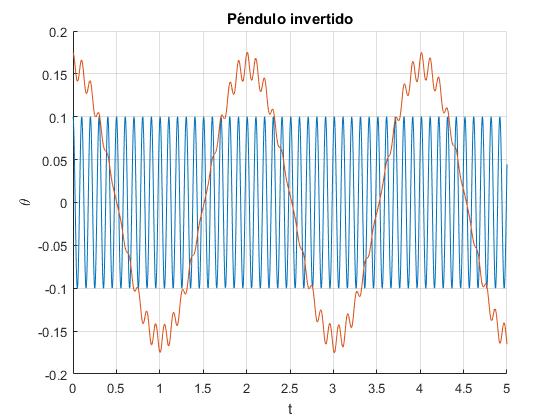
Representamos la oscilación θ(t) del péndulo y la oscilación del soporte, Acos(ωt) para una frecuencia angular ω grande en comparación con la frecuencia natural ω₀=3.13 rad/s para un péndulo de longitud l=1 m.

A=0.1; %amplitud de la oscilación del centro de suspensión
L=1; %longitud del péndulo
w0=sqrt(9.8/L); %frecuencia natural
w=20*w0;%frecuencia de oscilación del centro de suspensión
x0=[10*pi/180,0]; %condiciones iniciales, 10 grados
tspan=[0,5];
% x(1)=theta, x(2)=dtheta/dt,
fg=@(t,x)[x(2);(-A*w^2*cos(w*t)/L+w0^2)*sin(x(1))];
[t,x]=ode45(fg,tspan,x0);
hold on
fplot(@(t) A*cos(w*t),tspan)
plot(t, x(:,1)) 
hold off
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo invertido')

El centro de suspensión describe un movimiento circular

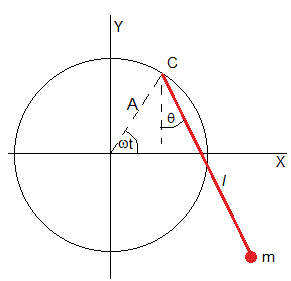
Supongamos un péndulo formado por una varilla inextensible y sin peso de longitud l, en cuyo extremo hay una partícula de masa m. El centro de suspensión describe un movimiento circular uniforme de radio A y con velocidad angular ω. Vamos a estudiar las oscilaciones forzadas de este sistema oscilante.

Establecemos un origen y unos ejes X e Y como se muestra en la figura. En un instante dado t la posición angular del centro de suspensión es ωt y el péndulo se ha desviado θ de la vertical.

La posición de la partícula de masa m es

${\displaystyle \{\begin{array}{l}x=A\cos \left(\omega t\right)+l\sin \theta \\ y=A\sin \left(\omega t\right)-l\cos \theta \end{array}}$

Derivando respecto del tiempo, obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=-\omega A\sin \left(\omega t\right)+l\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=\omega A\cos \left(\omega t\right)+l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\frac{1}{2}m\left({\omega }^2{A}^2+2Al\omega \sin \left(\theta -\omega t\right)\frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)}$

La energía potencial de la masa m es mgy

${\displaystyle V=mg\left(A\sin \left(\omega t\right)-l\cos \theta \right)}$

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left({\omega }^2{A}^2+2Al\omega \sin \left(\theta -\omega t\right)\frac{d\theta }{dt}+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)-mg\left(A\sin \left(\omega t\right)-l\cos \theta \right)\\ L=\frac{1}{2}m\left({\omega }^2{A}^2+2Al\omega \sin \left(\theta -\omega t\right)\dot{\theta }+l^2{\dot{\theta }}^2\right)-mg\left(A\sin \left(\omega t\right)-l\cos \theta \right)\end{array}}$

Ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ l\frac{d^2\theta }{d{t}^2}+g\sin \theta -A{\omega }^2\cos \left(\theta -\omega t\right)=0\end{array}}$

Para resolver la ecuación diferencial por procedimientos numéricos, despejamos la aceleración

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{A}{l}{\omega }^2\cos \left(\theta -\omega t\right)-{\omega }_0^2\sin \theta =0}$

Donde ${\omega }_0^2=g/l$ es la frecuencia natural de las oscilaciones del péndulo. Resolvemos la ecuación diferencial con las siguientes condiciones iniciales t=0, θ=θ₀, dθ/dt=0

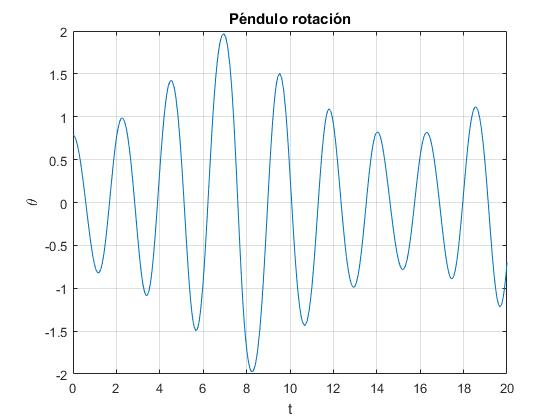
Representamos la posición angular θ del péndulo en función del tiempo t para una velocidad angular de rotación ω próxima a la frecuencia natural ω₀=3.1 rad/s para un péndulo de longitud l=1 m

L=1; %longitud del péndulo
w0=sqrt(9.8/L); %frecuencia natural
R=0.15; %radio de la circunferencia
w=3.1; %velocidad angular de rotación
%condiciones iniciales
x0=[pi/4,0]; %condiciones iniciales
tspan=[0,20];
% x(1)=theta, x(2)=dtheta/dt,
fg=@(t,x)[x(2); R*w^2*cos(x(1)-w*t)/L-w0^2*sin(x(1))];
[t,x]=ode45(fg,tspan,x0);
plot(t,x(:,1)) 
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo rotación')

Actividades

En primer lugar, especificamos los parámetros del sistema

• La velocidad angular de rotación del centro de suspensión del péndulo, el control titulado Velocidad angular
• La longitud del péndulo, se ha fijado en l=0.5
• El radio de la circunferencia que describe el centro de suspensión del péndulo, se ha fijado en A=0.15

En segundo lugar, especificamos las condiciones iniciales

• La desviación inicial θ₀ del péndulo en grados, en el control titulado Angulo inicial
• La velocidad inicial de la partícula a lo largo de la dirección tangencial se ha fijado en dθ/dt=0

Si queremos ver la gráfica de la posición angular θ del péndulo, activamos la casilla titulada Gráfica

Referencias

Leon Blitzer. Inverted pendulum. Am. J. Phys. 33 (1965), pp. 1076–1078

Landau, Lifshitz. Mecánica. Volumen I. Segunda Edición, Editorial Reverté, 1970, págs. 112-114

Rod Cross. Observations of a driven pendulum at low amplitudes. Eur. J. Phys. 42 (2021) 055001