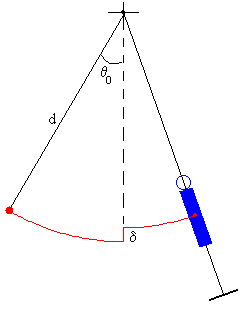
El columpio se utiliza de dos formas distintas:

• Un niño está sentado en la tabla, una persona le empuja periódicamente y en fase con su movimiento para incrementar o mantener la amplitud de las oscilaciones del columpio.

• Un niño que está montado en un columpio, en posición vertical sobre la tabla, mueve su cuerpo para lograr que la amplitud de la oscilación aumente.

Para explicar cualitativamente el funcionamiento de este columpio autopropulsado, supondremos que el centro de masas del niño repentinamente sube o baja en ciertas posiciones de la oscilación.

Se efectuará un análisis simplificado, en el que se considera al niño como una masa puntual situada en su centro de masas, que puede subir o bajar su c.m. una longitud δ mediante la acción de las fuerzas interiores. Se despreciará también el rozamiento del aire y en el eje del columpio.

Etapas del movimiento

En este apartado, haremos un análisis detallado de cada una de las etapas de un ciclo de las oscilaciones del columpio.

Primera etapa

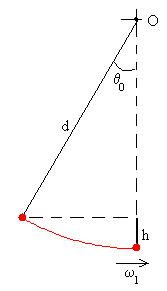
El columpio sale de la posición θ₀ con velocidad angular inicial nula ω=0. Llega a la posición de equilibrio θ=0, con una velocidad angular ω₁, que se calcula aplicando el principio de conservación de la energía.

${\displaystyle \frac{1}{2}(m{d}^2){\omega }_1^2=mgd(1-\cos {\theta }_0)}$

donde md² es el momento de inercia de una masa puntual m que dista d del eje de rotación O.

La energía total inicial es E₁=mgd(1-cosθ₀)

Segunda etapa

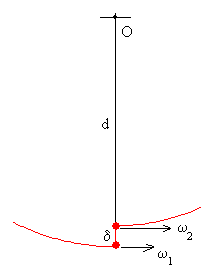
Cuando el columpio alcanza la posición de equilibrio θ=0, el niño sube su centro de masas (c.m.) una distancia δ. En ese preciso instante, el momento de las fuerzas que actúa sobre el columpio es cero (todas las fuerzas pasan por el origen O), el momento angular permanece constante.

${\displaystyle \frac{d\overrightarrow{L}}{dt}=\overrightarrow{M}\overrightarrow{M}=0\overrightarrow{L}=\text{cte}}$

• El momento angular inicial es md²·ω₁

• El momento angular final es m(d-δ)²·ω₂

La velocidad angular final ω₂ aumenta al disminuir la distancia al eje de rotación.

${\displaystyle {\omega }_2=\frac{d^2}{{\left(d-\delta \right)}^2}{\omega }_1}$

La energía total es

${\displaystyle E_2=\frac{1}{2}m{\left(d-\delta \right)}^2{\omega }_2^2+mg\delta }$

Balance energético

Calculamos en la posición de equilibrio θ=0, la energía inicial, la final y el trabajo que ejercen las fuerzas interiores para subir una altura δ el centro de masas del niño.

La energía inicial es

${\displaystyle E_i=\frac{1}{2}(m{d}^2){\omega }_1^2}$

La energía final es

${\displaystyle E_f=\frac{1}{2}m{\left(d-\delta \right)}^2{\omega }_2^2+mg\delta =\frac{1}{2}m\frac{d^4}{{\left(d-\delta \right)}^2}{\omega }_1^2+mg\delta }$

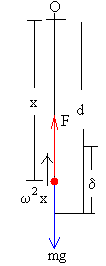
Para que el niño suba la posición de su centro de masas δ, ha de realizar un trabajo. Calculamos la fuerza F que han de ejercer sus músculos para que su c.m. describa un arco de circunferencia de radio x, aplicando la Dinámica del movimiento circular uniforme (fuerza=masa × aceleración normal)

F-mg=mω²x.

La constancia del momento angular en la posición de equilibrio θ=0 nos proporciona el valor de la velocidad angular ω cuando el c.m. está a una distancia x del eje de rotación O

md²·ω₁= mx²·ω

La fuerza F tiene el mismo sentido que el desplazamiento, el trabajo es positivo

${\displaystyle \begin{array}{l}W={\displaystyle \underset{d}{\overset{d-\delta }{\int }}(-F)·dx=}-{\displaystyle \underset{d}{\overset{d-\delta }{\int }}(mg+m{\omega }^{2}x)·dx}\\ =mg\delta +\frac{1}{2}m\frac{d^4}{{\left(d-\delta \right)}^2}{\omega }_1^2-\frac{1}{2}m{d}^4{\omega }_1^2\end{array}}$

Tercera etapa

Tenemos ahora la situación opuesta a la primera etapa, el columpio con una velocidad angular inicial ω₂ en la posición θ=0, alcanza un máximo desplazamiento angular θ₁. Aplicando el principio de conservación de la energía

${\displaystyle mg(d-\delta )(1-\cos {\theta }_1)=\frac{1}{2}m{\left(d-\delta \right)}^2{\omega }_2^2}$

El ángulo máximo θ₁ que se desvía el columpio es, combinado las expresiones anteriores

${\displaystyle \text{sin}\frac{{\theta }_1}{2}={\left(\frac{d}{d-\delta }\right)}^{\text{3/2}}\text{sin}\frac{{\theta }_0}{2}}$

como d>(d-δ) resulta que θ₁>θ₀

La energía total es

E₂=mg(d-δ)(1-cosθ₁)+mgδ=mgd(1-cosθ₁)+mgδcosθ₁

Cuarta etapa

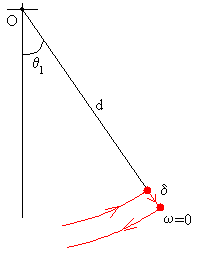
En la posición angular de desviación máxima θ₁, la velocidad angular ω=0. El niño baja la posición de su centro de masas en δ.

El único cambio que experimenta el sistema es una disminución de la energía potencial a cuenta del trabajo de las fuerzas internas. Poniendo en el eje O en nivel cero de la energía potencial.

ΔE_p=-mgdcosθ₁+mg(d-δ)cosθ₁= -mgδcosθ₁

La energía total es

E₃=mgd(1-cosθ₁)

Quinta etapa

Es similar a la primera etapa, el columpio se mueve hacia la posición de equilibrio estable θ=0, que alcanza con una velocidad angular ω₃. Aplicando el principio de conservación de la energía

${\displaystyle \frac{1}{2}(m{d}^2){\omega }_3^2=mgd(1-\cos {\theta }_1)}$

La energía total es E₃

Sexta etapa

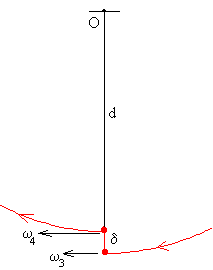
La sexta etapa es similar a la segunda etapa. En la posición de equilibrio estable, el centro de masas sube una altura δ. La velocidad angular se incrementa de nuevo de ω₃ a ω₄. La constancia del momento angular en la posición de equilibrio estable θ=0, nos proporciona el valor de la velocidad angular final ω₄.

${\displaystyle {\omega }_4=\frac{d^2}{{\left(d-\delta \right)}^2}{\omega }_3}$

La energía total es

${\displaystyle E_4=\frac{1}{2}m{\left(d-\delta \right)}^2{\omega }_4^2+mg\delta }$

Séptima etapa

La séptima etapa es similar a la tercera etapa. El columpio parte de la posición de equilibrio estable θ=0, con una velocidad angular inicial ω₄, alcanzando un desplazamiento máximo θ₂ que se obtiene aplicando el principio de conservación de la energía

${\displaystyle mg(d-\delta )(1-\cos {\theta }_2)=\frac{1}{2}m{\left(d-\delta \right)}^2{\omega }_4^2}$

Como ω₄> ω₃ el máximo desplazamiento θ₂ > θ₁

Relacionamos ambos desplazamientos mediante la fórmula

${\displaystyle \text{sin}\frac{{\theta }_2}{2}={\left(\frac{d}{d-\delta }\right)}^{3/2}\text{sin}\frac{{\theta }_1}{2}}$

La energía total es

E₄=mg(d-δ)(1-cosθ₂)+mgδ=mgd(1-cosθ₂)+mgδcosθ₂

Octava etapa

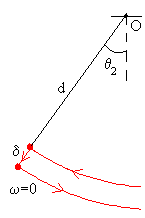
En la posición de máximo desplazamiento θ₂, ω=0, el centro de masa baja δ, con lo que se completa el primer ciclo de las oscilaciones del columpio.

La energía total es

E₅=mgd(1-cosθ₂)

Ecuaciones del movimiento del columpio entre las posiciones media y extremas

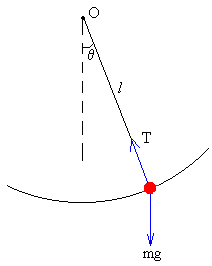
La ecuación del movimiento del columpio entre la posiciones extremas θ_i (i=0, 1, 2,3..) y la posición de equilibrio estable θ=0, es la misma que la de un péndulo de longitud l=d, l=d-δ, dependiendo de la distancia entre el c.m. y el eje O del columpio.

El momento angular de una partícula de masa m respecto del origen O es el producto del momento de inercia ml² por la velocidad angular ω, L=ml²·ω

El momento M de las fuerzas que actúan sobre la partícula respecto del origen O es

M=-mglsinθ

La ecuación del movimiento es dL/dt=M se escribe en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{dt}+\frac{g}{l}\text{sin}\theta =0}$

Se resuelve mediante procedimientos numéricos, con las condiciones iniciales que dependen de cada etapa del movimiento:

• en la primera etapa, l=d, θ=θ₀, dθ/dt=0
• en la tercera etapa, l=d-δ, θ=0, dθ/dt=ω₂
• en la quinta etapa, l=d, θ=θ₁, dθ/dt=0
• en la séptima etapa,l=d-δ, θ=0, dθ/dt=ω₄
• y así sucesivamente...

Resumiendo

• El columpio debe de estar desplazado inicialmente un ángulo θ₀>0, para que pueda funcionar el mecanismo descrito en esta página.

• El c.m. del niño sube y baja de forma instantánea por la acción de las fuerzas internas, en la posición de equilibrio y en las posiciones de máximo desplazamiento.

• Mediante el mecanismo que se ha descrito, el trabajo de las fuerzas internas (acción de los músculos) se invierte en incrementar el máximo desplazamiento del columpio de modo que θ₀<θ₁<θ₂<θ₃<… Teóricamente, el columpio puede llegar a dar una vuelta completa.

En el primer ciclo completo, el desplazamiento máximo θ₂ vale

${\displaystyle \text{sin}\frac{{\theta }_2}{2}={\left(\frac{d}{d-\delta }\right)}^3\text{sin}\frac{{\theta }_0}{2}}$

Si el centro de masas se eleva y desciende una altura δ pequeña comparada con la longitud d del columpio

${\displaystyle \text{sin}\frac{{\theta }_2}{2}={\left(1-\frac{\delta }{d}\right)}^{-3}\text{sin}\frac{{\theta }_0}{2}\text{sin}\frac{{\theta }_2}{2}\approx \left(1+\frac{3\delta }{d}\right)\text{sin}\frac{{\theta }_0}{2}}$

En el segundo ciclo

${\displaystyle \text{sin}\frac{{\theta }_4}{2}={\left(\frac{d}{d-\delta }\right)}^6\text{sin}\frac{{\theta }_0}{2}\text{sin}\frac{{\theta }_4}{2}\approx {\left(1+\frac{3\delta }{d}\right)}^{\text{2}}\text{sin}\frac{{\theta }_0}{2}}$

y así, sucesivamente.

• La energía total al finalizar la segunda oscilación vale

${\displaystyle \begin{array}{l}{E}_2=mgd\left(1-\cos {\theta }_4\right)=2mgd·{\sin }^2\frac{{\theta }_4}{2}\approx 2mgd\left(1+\frac{3\delta }{d}\right){\sin }^2\frac{{\theta }_0}{2}=\\ E_0{\left(1+\frac{3\delta }{d}\right)}^4\end{array}}$

donde E₀ es la energía inicial del columpio. Después de n oscilaciones

${\displaystyle E_n\approx E_0{\left(1+\frac{3\delta }{d}\right)}^{2n}}$

La energía crece exponencialmente independientemente de la masa del niño y depende solamente del desplazamiento relativo δ/d del c.m. del niño en las posiciones extremas y en el medio de la oscilación.

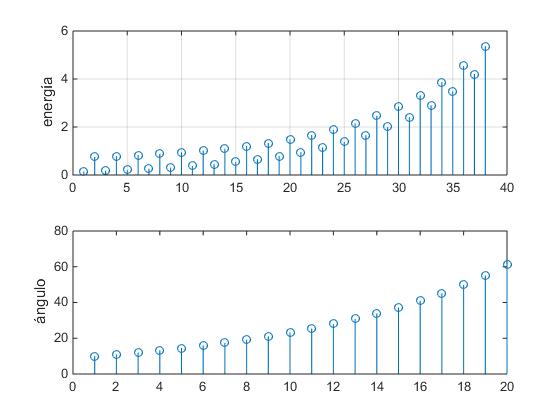
Ejemplo

• El desplazamiento angular inicial θ₀=10º
• El desplazamiento del c.m. δ=6 cm=0.06 m
• La distancia inicial d=1.0 entre le c.m. y eje de rotación O.

En la figura se muestra un ciclo completo de operación del columpio

1.-La energía inicial es E₁=mgd(1-cosθ₀)=m·9.8·1.0·(1-cos10º)=0.15·m

2.-Se aplica el principio de conservación de la energía. La velocidad angular ω₁ en la posición de equilibrio es

${\displaystyle \frac{1}{2}(m·1^2){\omega }_1^2=m·9.8·1(1-\cos 10º){\omega }_1=0.55\text{rad/s}}$

La energía E₂=E₁

3.-El centro de masa asciende, se conserva el momento angular

md²·ω₁=m(d-δ)²·ω₂, ω₂ =0.62 rad/s

La energía total es

${\displaystyle E_3=\frac{1}{2}m{(1-0.06)}^2{0.62}^2+m·9.8·0.06=0.76\text{·}m}$

4.-La energía cinética se convierte en energía potencial, el columpio se desvía un ángulo θ₁

${\displaystyle m·9.8(1-0.06)(1-\cos {\theta }_1)=\frac{1}{2}m{(1-0.06)}^2{0.62}^2{\theta }_1=11º}$

La energía E₄=E₃

5.-El centro de masas desciende, la energía total es

E₅=m9.8·1(1-cos11º)=0.18·m

6.-Se aplica el principio de conservación de la energía. La velocidad angular ω₃ en la posición de equilibrio es

${\displaystyle \frac{1}{2}(m·1^2){\omega }_3^2=m·9.8·1(1-\cos 11º){\omega }_3=0.60\text{rad/s}}$

La energía E₆=E₅

7.-El centro de masa asciende, se conserva el momento angular

md²·ω₃=m(d-δ)²·ω₄, ω₄ =0.68 rad/s

La energía total es

${\displaystyle E_7=\frac{1}{2}m{(1-0.06)}^2{0.68}^2+m·9.8·0.06=0.79\text{·}m}$

8.-La energía cinética se convierte en energía potencial, el columpio se desvía un ángulo θ₂

${\displaystyle m·9.8(1-0.06)(1-\cos {\theta }_2)=\frac{1}{2}m{(1-0.06)}^2{0.68}^2{\theta }_2=12º}$

La energía E₈=E₇

9.-El centro de masas desciende, la energía total es

E₉=m9.8·1(1-cos12º)=0.22·m

10.-Comienza un nuevo ciclo.

Los desplazamientos máximos se pueden calcular mediante las fórmulas

${\displaystyle \text{sin}\frac{{\theta }_1}{2}={\left(\frac{d}{d-\delta }\right)}^{3/2}\text{sin}\frac{{\theta }_0}{2}\text{sin}\frac{{\theta }_1}{2}={\left(\frac{1.0}{1.0-0.06}\right)}^{3/2}\text{sin}\frac{10º}{2}{\theta }_1=11º}$

Aplicamos la misma fórmula para calcular el desplazamiento máximo θ₂, conocido θ₁.

${\displaystyle \text{sin}\frac{{\theta }_2}{2}={\left(\frac{d}{d-\delta }\right)}^{3/2}\text{sin}\frac{{\theta }_1}{2}\text{sin}\frac{{\theta }_2}{2}={\left(\frac{1.0}{1.0-0.06}\right)}^{3/2}\text{sin}\frac{11º}{2}{\theta }_2=12º}$

y así sucesivamente...

clear
fi=10*pi/180;  %ángulo inicial de partida
delta=0.06;   %desplazamiento del c.m.
d=1;           %longitud del columpio
e=zeros(0,40);
angulo=zeros(0,20);
E=9.8*d*(1-cos(fi));  %energía inicial
e(1)=E;
angulo(1)=fi*180/pi;
for i=1:20
  E=E*(d/(d-delta))^2+9.8*delta; %energía al pasar por la posición fi=0
  e(2*i)=E;
  fi=2*asin((d/(d-delta))^(3/2)*sin(fi/2)) %desplazamiento angular máximo
  angulo(i+1)=fi*180/pi;
  if fi>pi/3 %no supera los 60º
      break
  end
  E=9.8*d*(1-cos(fi)); %energía final en los extremos
  e(2*i+1)=E;
end
subplot(2,1,1)
stem(e)
grid on
ylabel('energía')
subplot(2,1,2)
stem(angulo)
ylabel('ángulo')

Actividades

Se introduce

• El desplazamiento angular inicial θ₀>0, un ángulo en grados en el control titulado Angulo inicial

• El desplazamiento δ del centro de masas, en cm, en el control titulado Desplazamiento.

• La distancia inicial del c.m. al eje de rotación O se ha fijado en d=1.0 m.

Se pulsa el botón titulado Nuevo

Se observa el movimiento del columpio, y el cambio de posición del c.m. del niño representado por un punto de color rojo, cuando el columpio pasa por las posiciones de máximo desplazamiento ω=0, por la posición de equilibrio estable θ=0.

En la parte derecha, se muestra la energía total del columpio. El nivel cero de energía potencial se ha establecido en la parte más baja de la trayectoria del c.m, es decir, en la posición del c.m. cuando el columpio está en equilibrio θ₀=0. Observamos dónde cambia la energía total, dónde se conserva, transformándose la energía potencial en cinética y viceversa.

Cuando el columpio se desvía un ángulo mayor que 60º, se detiene

Péndulo de longitud variable

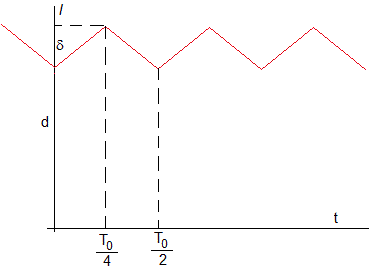
Hemos supuesto que el centro de masas del niño se eleva δ en la posición θ=0, (la longitud del péndulo pasa de d a d-δ) y desciende en los extremos θ₀ de la oscilación, (la longitud del péndulo pasa de d-δ a d) en un tiempo muy corto comparado con el periodo T₀ de la oscilación que supondremos constante e independiente de la amplitud θ₀

En este apartado, supondremos el tiempo que tarda el centro de masas del niño en elevarse o descender es T₀/4. En la figura, en color rojo, se muestra la longitud l=d-f(t) del péndulo en función del tiempo

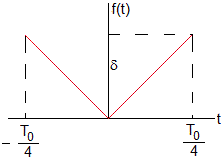
Hacemos un análisis de Fourier de la función periódica

${\displaystyle f(t)=\{\begin{array}{l}-\delta \frac{t}{P}-P\le t\le 0\\ \delta \frac{t}{P}0\le t\le P\end{array}}$

Siendo P=T₀/4. Dado que f(t) es una función par, los coeficientes b_k=0

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)}dt=\frac{1}{P}\left\{{\displaystyle \underset{-P}{\overset{0}{\int }}\left(-\delta \frac{t}{P}\right)}dt+{\displaystyle \underset{0}{\overset{P}{\int }}\left(\delta \frac{t}{P}\right)}dt\right\}=\delta \\ a_k=\frac{1}{P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)\cos \frac{k\pi t}{P}}dt=\\ \frac{1}{P}\left\{{\displaystyle \underset{-P}{\overset{0}{\int }}\left(-\delta \frac{t}{P}\right)\cos \frac{k\pi t}{P}}dt+{\displaystyle \underset{0}{\overset{P}{\int }}\left(\delta \frac{t}{P}\right)\cos \frac{k\pi t}{P}}dt\right\}=\end{array}}$

Hacemos una integración por partes

${\displaystyle \begin{array}{l}\frac{\delta }{P^2}\left\{{-\left(t\frac{P}{k\pi }\sin \frac{k\pi t}{P}+\frac{P^2}{k^2{\pi }^2}\cos \frac{k\pi t}{P}\right)|}_{-P}^0+{\left(t\frac{P}{k\pi }\sin \frac{k\pi t}{P}+\frac{P^2}{k^2{\pi }^2}\cos \frac{k\pi t}{P}\right)|}_0^P\right\}=\\ =\{\begin{array}{l}\frac{4\delta }{k^2{\pi }^2},k=\mathrm{1,3,5...}\\ \mathrm{0,}k=\mathrm{2,4,6...}\end{array}\end{array}}$

El resultado es

${\displaystyle f(t)=\frac{\delta }{2}+\frac{4\delta }{{\pi }^2}{\displaystyle \sum _{k=\mathrm{1,3,5..}}^{\infty }\frac{1}{k^2}\cos \frac{k\pi t}{P}}}$

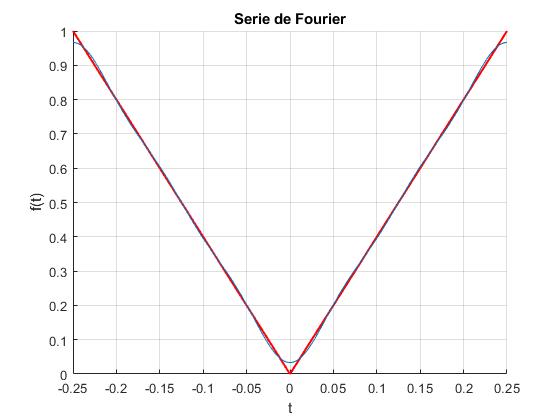
Utilizamos MATLAB para calcular los coeficientes a_k y b_k y aproximar la función f(t) a un número finito de términos 1, 3 y 5

syms t;
N=5; %términos del desarrollo en serie
T0=1;
P=T0/4;
d=1;
%definición de la fuerza y su semiperiodo P
f=@(t) (-d*t/P)*(heaviside(t+P)-heaviside(t))+(d*t/P)*(heaviside(t)-heaviside(t-P));
a = @(k) int(f*cos(k*pi*t/P),t,-P,P)/P;
b = @(k) int(f*sin(k*pi*t/P),t,-P,P)/P;
fs=a(0)/2;
for k=1:N %número de términos
    fs=fs+a(k)*cos(k*pi*t/P)+b(k)*sin(k*pi*t/P);
end
hold on
line([-T0/4,0],[d,0],'lineWidth',1.5, 'color','r')
line([0,T0/4],[0,d],'lineWidth',1.5, 'color','r')
fplot(fs,[-T0/4,T0/4]);
hold off
grid on
xlabel('t')
ylabel('f(t)')
title('Serie de Fourier')

Añadimos estas líneas de código para representar los coeficientes a_k y b_k

...
figure
k=1:N;
ak=a(k);
bk=b(k);
subplot(2,1,1)
stem(ak)
grid on
xlabel('k');
ylabel('a(k)')

subplot(2,1,2)
stem(bk)
grid on
xlabel('k');
ylabel('b(k)')

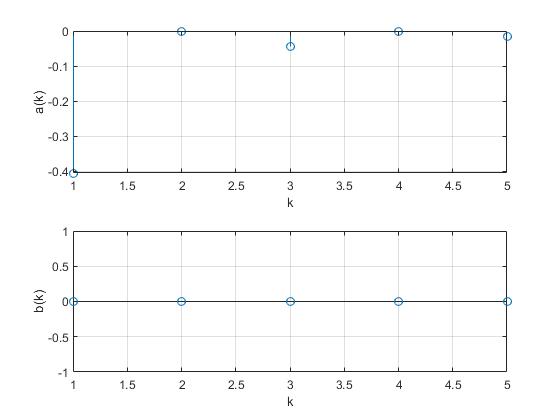
Observamos que los coeficientes b_k son nulos ya que la función f(t) tiene simetría par, son también nulos los coeficientes pares a₂, a₄, .... El coeficiente más importante es a₁, los otros a₃, a₅... son comparativamente mucho más pequeños. La función f(t) se puede describir aproximadamente con el coeficiente a₀ y el primer término de la serie, tal como se muestra en esta figura

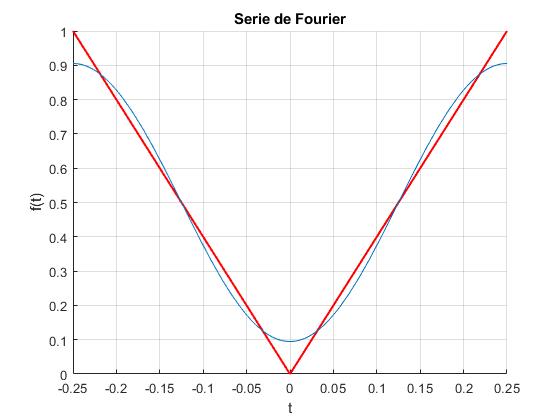
Con esta aproximación, la longitud l del péndulo es una función del tiempo de la forma

${\displaystyle l=d-\frac{\delta }{2}-\frac{4\delta }{{\pi }^2}\cos \frac{4\pi t}{T_0}=d-\frac{\delta }{2}-\frac{4\delta }{{\pi }^2}\cos \left(2{\omega }_{0}t\right)=l_0\left(1-h\cos \left(2{\omega }_{0}t\right)\right)}$

La ecuación diferencial del movimiento del péndulo se escribe

${\displaystyle \begin{array}{l}\frac{d^2\theta }{dt}+\frac{g}{l_0\left(1-h\cos \left(2{\omega }_{0}t\right)\right)}\theta =\mathrm{0,}h<<1\\ \frac{d^2\theta }{dt}+{\omega }_0^2\left(1+h\cos \left(2{\omega }_{0}t\right)\right)\theta =0\end{array}}$

Cuando la frecuencia de ω(t) es aproximadamente del doble de ω₀ se produce una resonancia paramétrica. En el caso de que el rozamiento sea despreciable, la amplitud crece exponencialmente con el tiempo. Una situación similar se estudia en la página titulada 'péndulo elástico'

Referencias

Tea P., Falk H. Pumping on a swing. Am. J. Phys. 36 (1968) 1165-1166

Para el apartado titulado 'Péndulo de longitud variable'

Bejo Duka, Raimonda Duka. On the elastic pendulum, parametric resonance and 'pumping' swings. Eur. J. Phys. 40 (2019), 025005