Pulso triangular

Sea la fuerza

${\displaystyle F(t)=\{\begin{array}{l}\frac{F_0}{a}t0\le t\le a\\ 0t>a\end{array}}$

Su transformada de Laplace es

${\displaystyle \begin{array}{l}f(t)=\frac{F(t)}{m}=\left(u(t)-u(t-a)\right)\frac{F_0}{m}\frac{t}{a}\\ =\frac{f_0}{a}\left(t-u(t-a)(t-a)-u(t-a)a\right)\\ g(s)=\frac{f_0}{a}\left(\frac{1}{s^2}-\frac{\exp (-as)}{s^2}-a\frac{\exp (-as)}{s}\right)\end{array}}$

Para el caso de que las condiciones iniciales sean: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0. La transformada de Laplace de la ecuación diferencial que describe el comportamiento del oscilador de frecuencia propia ω₀ y coeficiente de la fuerza de rozamiento γ, es F(s)

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=f(t)\\ F(s)=\frac{f_0}{a}\left(\frac{1}{s^2}-\frac{\exp (-as)}{s^2}-a\frac{\exp (-as)}{s}\right)\frac{1}{s^2+2\gamma s+{\omega }_0^2}\end{array}}$

Descomponemos la fracción de la izquierda en suma de fracciones más simples

${\displaystyle \begin{array}{l}\frac{1}{s\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{A_1}{s}+\frac{C_{1}s+D_1}{s^2+2\gamma s+{\omega }_0^2}\\ A_1=\frac{1}{{\omega }_0^2}{C}_1=-\frac{1}{{\omega }_0^2}{D}_{{}_1}=-\frac{2\gamma }{{\omega }_0^2}\\ \frac{1}{s^2\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{A_2}{s}+\frac{B_2}{s^2}+\frac{C_{2}s+D_2}{s^2+2\gamma s+{\omega }_0^2}\\ A_2=-\frac{2\gamma }{{\omega }_0^4}{B}_2=\frac{1}{{\omega }_0^2}{C}_2=\frac{2\gamma }{{\omega }_0^4}{D}_{{}_2}=\frac{4{\gamma }^2-{\omega }_0^2}{{\omega }_0^4}\end{array}}$

Escribimos F(s) en forma apropiada para obtener la transformada inversa de Laplace, mirando a las tablas.

${\displaystyle \begin{array}{l}F(s)=\frac{f_0}{a}\left(\frac{A_2}{s}+\frac{B_2}{s^2}+\frac{C_{2}s+D_2}{s^2+2\gamma s+{\omega }_0^2}\right)\\ -\frac{f_0}{a}\exp (-as)\left(\frac{A_2}{s}+\frac{B_2}{s^2}+\frac{C_{2}s+D_2}{s^2+2\gamma s+{\omega }_0^2}\right)\\ -f_0\exp (-as)\left(\frac{A_1}{s}+\frac{C_{1}s+D_1}{s^2+2\gamma s+{\omega }_0^2}\right)\end{array}}$

La transformada inversa de Laplace es

${\displaystyle \begin{array}{l}x(t)=\frac{f_0}{a}\left(g(t)-u(t-a)g(t-a)+a·u(t-a)h(t-a)\right)\\ h(t)=A_1+C_1\exp (-\gamma t)\cos (\omega t)+\left(\frac{D_1-C_1\gamma }{\omega }\right)\exp (-\gamma t)\sin (\omega t)\\ g(t)=A_2+B_{2}t+C_2\exp (-\gamma t)\cos (\omega t)+\left(\frac{D_2-C_2\gamma }{\omega }\right)\exp (-\gamma t)\sin (\omega t)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

Aplicamos a un oscilador de frecuencia propia ω₀=4, coeficiente de la fuerza de rozamiento proporcional a la velocidad γ=0. La fuerza dura un tiempo a=0.4 s y su valor máximo es f₀=F₀/m=40.

g=0; %rozamiento
w0=4; %frecuencia propia del oscilador
F0=40; %máximo valor de la fuerza
a=0.4; %tiempo de la fuerza

A1=1/w0^2;
C1=-1/w0^2;
D1=-2*g/w0^2;

A2=-2*g/w0^4;
B2=1/w0^2;
C2=2*g/w0^4;
D2=(4*g^2-w0^2)/w0^4;
w=sqrt(w0^2-g^2);

h=@(t) A1+C1*exp(-g*t).*cos(w*t)+(D1-C1*g)*exp(-g*t).*sin(w*t)/w;
g=@(t) A2+B2*t+C2*exp(-g*t).*cos(w*t)+(D2-C2*g)*exp(-g*t).*sin(w*t)/w;

t=linspace(0,2.4,200);
x=F0*(g(t)-g(t-a).*heaviside(t-a)-a*h(t-a).*heaviside(t-a))/a;
plot(t,x)
ylabel('x(t)')
xlabel('t')
title('Pulso F_0·(t/a)')
grid on

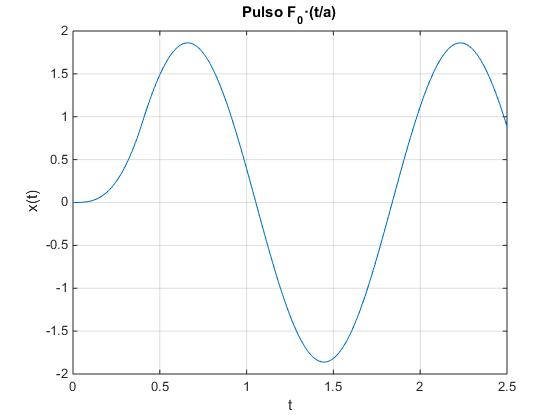
Obtenemos un resultado similar empleando Math Symbolic, salvo que aparece un error cuando se describe el oscilador sin rozamiento γ=0.

>> syms w0 g s t;
>> ft=100*(1-heaviside(t-0.4))*t;
>> gs=laplace(ft);
>> Fs=gs/(s^2+2*g*s+w0^2);
>> x=ilaplace(Fs);
>> xx=subs(x,{g,w0},{0.001,4}); %rozamiento muy pequeño
>> ezplot(xx,[0 2.4])
>> grid on
>> ylabel('x(t)')
>> xlabel('t')
>> title('Pulso F_0·(t/a)')

Función rampa

Aplicamos una fuerza de la forma F₀·t/a durante un tiempo a≤2, la fuerza es F₀ para t>a.

La función f(t) se define

${\displaystyle \begin{array}{l}f(t)=\frac{F(t)}{m}=\left(u(t)-u(t-a)\right)f_0\frac{t}{a}+u(t-a)f_0=\\ \frac{f_0}{a}\left(t-u(t-a)\left(t-a\right)\right)\end{array}}$

Su transformada de Laplace g(s) es

${\displaystyle g(s)=\frac{f_0}{a}\left(\frac{1}{s^2}-\frac{\exp (-as)}{s^2}\right)}$

Para un oscilador de frecuencia propia ω₀ y coeficiente de la fuerza de rozamiento γ, y para las condiciones iniciales: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0, calculamos la transformada inversa de Laplace de la función.

${\displaystyle F(s)=\frac{f_0}{a}\left(\frac{1}{s^2}-\frac{\exp (-as)}{s^2}\right)\frac{1}{s^2+2\gamma s+{\omega }_0^2}}$

Expresamos la siguiente fracción como suma de fracciones más simples

${\displaystyle \begin{array}{l}\frac{1}{s^2\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{A}{s}+\frac{B}{s^2}+\frac{Cs+D}{s^2+2\gamma s+{\omega }_0^2}\\ A=-\frac{2\gamma }{{\omega }_0^4}B=\frac{1}{{\omega }_0^2}C=\frac{2\gamma }{{\omega }_0^4}D=\frac{4{\gamma }^2-{\omega }_0^2}{{\omega }_0^4}\end{array}}$

Escribimos F(s) en forma apropiada para obtener la transformada inversa de Laplace, mirando a las tablas.

${\displaystyle \begin{array}{l}F(s)=f_0{\omega }_f\left(\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\right)+\\ f_0\frac{\pi }{a}\exp (-as)\left(\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\right)\\ x(t)=f_0{\omega }_f\left(g(t)+u(t-a)g(t-a)\right)\\ g(t)=A\cos \left({\omega }_{f}t\right)+B\sin \left({\omega }_{f}t\right)+C\exp (-\gamma t)\cos (\omega t)+\left(\frac{D-C\gamma }{\omega }\right)\exp (-\gamma t)\sin (\omega t)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}{\omega }_f=\frac{\pi }{a}\end{array}}$

Representamos gráficamente x(t) para f₀=10, γ=0.5, ω₀=3 rad/s

g=0.5; %rozamiento
w0=3; %frecuencia propia
f0=10; %valor máximo de la fuerza
a=2; %anchura del pulso

A=-2*g/w0^4;
B=1/w0^2;
C=2*g/w0^4;
D=(4*g^2-w0^2)/w0^4;
w=sqrt(w0^2-g^2);
g=@(t) A+B*t+C*exp(-g*t).*cos(w*t)+(D-C*g)*exp(-g*t).*sin(w*t)/w;

t=linspace(0,10,400);
x=f0*(g(t)-heaviside(t-a).*g(t-a))/a;
plot(t,x)
ylabel('x(t)')
xlabel('t')
title('Pulso rampa')
grid on

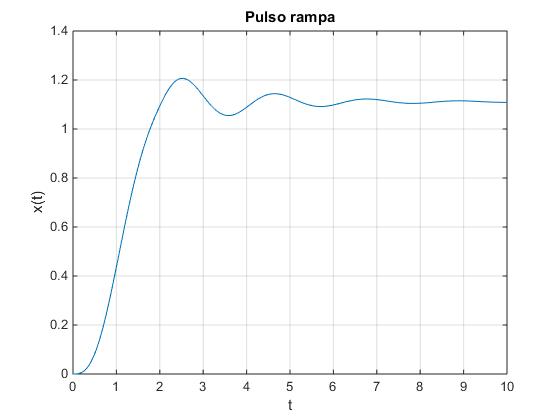
Obtenemos un resultado similar empleando Math Symbolic.

>> syms a t s g w0 f0;
>> ft=f0*(t-heaviside(t-a)*(t-a))/a;
>> gs=laplace(ft);
>> Fs=gs/(s^2+2*g*s+w0^2);
>> x=ilaplace(Fs);
>> xx=subs(x,{g w0 f0 a},{0.5 3 10 2});
>> ezplot(xx,[0 10])
>> grid on
>> ylabel('x(t)')
>> xlabel('t')
>> title('Pulso rampa')

Pulso media onda

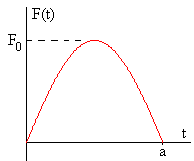
Aplicamos una fuerza de la forma F(t)=F₀·sin(ω_ft) durante un tiempo a=π/ω_f. La función f(t) se define

${\displaystyle f(t)=\frac{F(t)}{m}=\{\begin{array}{l}{f}_0\sin ({\omega }_{f}t)0\le t\le a\\ 0t>a\end{array}}$

La transformada de Laplace de esta función se calcula a partir de su definición, integrando dos veces por partes.

${\displaystyle g(s)={\displaystyle {\int }_0^{\infty }{e}^{-st}f(t)·dt=f_0{\displaystyle {\int }_0^a{e}^{-st}\sin \left(\frac{\pi }{a}t\right)·dt=}}{f}_0{\omega }_f\frac{1+\exp (-as)}{{\omega }_f^2+s^2}}$

Para un oscilador de frecuencia propia ω₀ y coeficiente de la fuerza de rozamiento γ, y para las condiciones iniciales: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0, calculamos la transformada inversa de Laplace de la función.

${\displaystyle F(s)=f_0{\omega }_f\frac{1+\exp (-as)}{{\omega }_f^2+s^2}\frac{1}{s^2+2\gamma s+{\omega }_0^2}}$

Expresamos la siguiente fracción como suma de fracciones más simples

${\displaystyle \begin{array}{l}\frac{1}{\left(s^2+{\omega }_f^2\right)\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{s^2+2\gamma s+{\omega }_0^2}\\ A=\frac{-2\gamma }{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2}B=\frac{{\omega }_0^2-{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2}\\ C=\frac{2\gamma }{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2}D=\frac{4{\gamma }^2-{\omega }_0^2+{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2}\end{array}}$

Escribimos F(s) en forma apropiada para obtener la transformada inversa de Laplace, mirando a las tablas.

${\displaystyle \begin{array}{l}F(s)=f_0{\omega }_f\left(\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\right)+\\ f_0\frac{\pi }{a}\exp (-as)\left(\frac{As+B}{s^2+{\omega }_f^2}+\frac{Cs+D}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\right)\\ x(t)=f_0{\omega }_f\left(g(t)+u(t-a)g(t-a)\right)\\ g(t)=A\cos \left({\omega }_{f}t\right)+B\sin \left({\omega }_{f}t\right)+C\exp (-\gamma t)\cos (\omega t)+\left(\frac{D-C\gamma }{\omega }\right)\exp (-\gamma t)\sin (\omega t)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}{\omega }_f=\frac{\pi }{a}\end{array}}$

Representamos gráficamente x(t) para f₀=1, γ=1, a=π, ${\omega }_0=\sqrt{3}$ rad/s

g=1; %rozamiento
f0=1; %amplitud de la fuerza
w0=sqrt(3); %frecuencia propia del oscilador
a=pi;       %semiperiodo
wf=pi/a;    %frecuencia de la fuerza oscilante

A=-2*g/((w0^2-wf^2)^2+4*g^2);
C=-A;
B=(w0^2-wf^2)/((w0^2-wf^2)^2+4*g^2);
D=(wf^2-w0^2+4*g^2)/((w0^2-wf^2)^2+4*g^2);
w=sqrt(w0^2-g^2);
g=@(t) A*cos(wf*t)+(B/wf)*sin(wf*t)+
C*exp(-g*t).*cos(w*t)+(D-C*g)*exp(-g*t).*sin(w*t)/w;

t=linspace(0,10,100);
x=f0*wf*(g(t)+heaviside(t-a).*g(t-a));
plot(t,x)
ylabel('x(t)')
xlabel('t')
title('Pulso sin(t)')
grid on

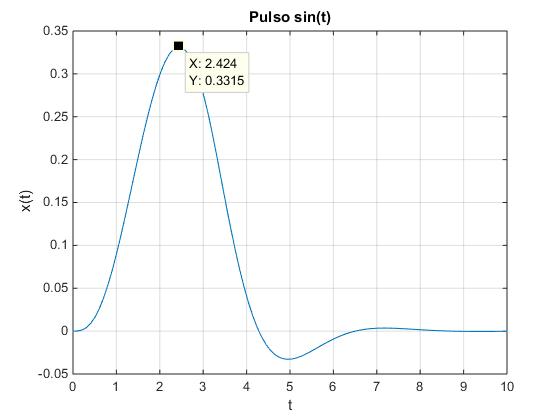
El máximo valor del desplazamiento es 0.3315 en el instante 2.424

Obtenemos un resultado similar empleando Math Symbolic.

>> syms a t s g w0 f0;
>> ft=f0*(1-heaviside(t-a))*sin(pi*t/a);
>> gs=laplace(ft);
>> Fs=gs/(s^2+2*g*s+w0^2);
>> x=ilaplace(Fs);
>> xx=subs(x,{g w0 f0 a},{1 sqrt(3) 1 pi});
>> ezplot(xx,[0 10])
>> grid on
>> ylabel('x(t)')
>> xlabel('t')
>> title('Pulso seno')

Nota: La versión 2014 de MATLAB no ejecuta este código, da un mensaje de error 'Division by zero'. Sin embargo, es ejecutado sin problemas por la versión 2007