Vamos a estudiar ahora el comportamiento de un oscilador forzado bajo la acción de una fuerza F(t).

Aplicamos la segunda ley de Newton a este sistema

ma=-λv-kx+F(t)

Que escribimos en forma de ecuación diferencial general, con las siguientes condiciones iniciales: posición inicial x₀ y velocidad inicial v₀ en el instante t=0

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=f(t)f(t)=\frac{F(t)}{m}\\ t=0\{\begin{array}{l}x=x_0\\ \frac{dx}{dt}=v_0\end{array}\end{array}}$

• ω₀ es la frecuencia natural o propia del oscilador
• γ es la constante de amortiguamiento,  γ<ω₀

Aplicamos la transformada de Laplace a la ecuación diferencial

${\displaystyle \begin{array}{l}\left(s^{2}F(s)-s·x(0)-x\text{'}(0)\right)+2\gamma \left(sF(s)-x(0)\right)+{\omega }_0^{2}F(s)=g(s)\\ \left(s^{2}F(s)-s·x_0-v_0\right)+2\gamma \left(sF(s)-x_0\right)+{\omega }_0^{2}F(s)=g(s)\\ F(s)=\frac{g(s)}{s^2+2\gamma s+{\omega }_0^2}+\frac{s{x}_0+2\gamma x_0+v_0}{s^2+2\gamma s+{\omega }_0^2}\end{array}}$

g(s) es la transformada de Laplace de la función f(t)

La transformada inversa de Laplace x(t)=x₁(t)+x₂(t) es la suma de dos términos, el primero es el debido a la fuerza y no depende de las condiciones iniciales y el segundo depende de los valores de la posición inicial x₀ y velocidad inicial v₀ en el instante t=0.

Como hemos visto en la página anterior: oscilaciones amortiguadas, la transformada inversa de Laplace del segundo término x₂(t) es

${\displaystyle \begin{array}{l}{x}_2=x_0{e}^{-\gamma t}\cos (\omega t)+\frac{\left(\gamma x_0+v_0\right)}{\omega }{e}^{-\gamma t}\sin (\omega t)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

Quedaría por determinar la transformada inversa de Laplace del primer término que dependerá de la función g(s) particular, es decir, de la fuerza aplicada a la partícula en función del tiempo t, F(t).

Pulso delta de Dirac

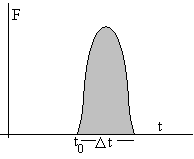
Un impulso es una fuerza F(t) actuando durante un tiempo Δt. Por ejemplo, un golpe de un martillo, el choque de un objeto contra otro fijo, la presión de los gases de una explosión, etc.

Se define impulso como el área sombreada bajo la curva F(t), o la integral

${\displaystyle I={\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}F(t)·dt}}$

El impulso unidad o la función delta de Dirac se define

${\displaystyle \begin{array}{l}\delta (t-a)=0t\ne a\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (t-a)·dt}=1\end{array}}$

La fuerza es nula excepto en las proximidades de t=a. El valor de la fuerza es muy grande en ese instante.

Un impulso I₀ que puede representar una fuerza muy grande actuando durante un intervalo muy corto de tiempo se puede escribir.

${\displaystyle \begin{array}{l}I(t)=I_0·\delta (t)\\ f(t)=\frac{I_0}{m}\delta (t)\end{array}}$

La transformada de Laplace g(s) es, véase la tabla de transformadas de Laplace

${\displaystyle g(s)=\frac{I_0}{m}}$

Se procede a calcular la transformada inversa de Laplace de modo similar al del oscilador amortiguado, ya que solamente se añade el término constante I₀/m, por lo que la acción del impulso es proporcionar al móvil una velocidad inicial adicional I₀/m, tal como vemos a continuación.

${\displaystyle \begin{array}{l}F(s)=\frac{I_0/m}{s^2+2\gamma s+{\omega }_0^2}+\frac{s{x}_0+2\gamma x_0+v_0}{s^2+2\gamma s+{\omega }_0^2}=\\ F(s)=\frac{x_0(s+\gamma )}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}+\frac{\left(\gamma x_0+v_0+I_0/m\right)}{\sqrt{{\omega }_0^2-{\gamma }^2}}\frac{\sqrt{{\omega }_0^2-{\gamma }^2}}{{(s+\gamma )}^2+({\omega }_0^2-{\gamma }^2)}\\ x(t)=x_0{e}^{-\gamma t}\cos (\omega t)+\frac{\left(\gamma x_0+v_0+I_0/m\right)}{\omega }{e}^{-\gamma t}\sin (\omega t)\\ x(t)=x_0\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)+\frac{v_0+I_0/m}{\omega }\exp (-\gamma t)\sin (\omega t)\end{array}}$

Para el caso de que las condiciones iniciales sean: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle x(t)=\frac{I_0}{m\omega }\exp (-\gamma t)\sin (\omega t)}$

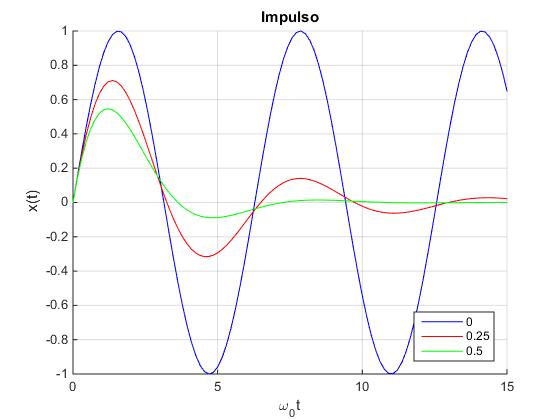
Vamos a representar la función x(t) en función de ω₀t para varios valores del coeficiente de rozamiento γ=ω₀·g. Escribimos la función x(t) de forma apropiada

${\displaystyle \begin{array}{l}x(t)=\frac{I_0}{m{\omega }_0^2}\frac{1}{\sqrt{1-g^2}}\exp (-g{\omega }_{0}t)\sin \left(\sqrt{1-g^2}{\omega }_{0}t\right)\\ \gamma =g{\omega }_0\omega ={\omega }_0\sqrt{1-g^2}\end{array}}$

r=[0 0.25 0.5]; %rozamiento ξ
col=['b' 'r' 'g']; %colores
t=linspace(0,15,100); %w0·t en el eje horizontal
hold on
i=0;
for g=r
    i=i+1;
    x=exp(-g*t).*(sin(sqrt(1-g^2)*t))/sqrt(1-g^2);
    plot(t,x,col(i),'displayName',num2str(r(i)))
end
title('Impulso')
xlabel('\omega_0t')
ylabel('x(t)')
legend('-DynamicLegend','location','Southeast')
grid on
hold off

Función escalón

Supongamos ahora, que la fuerza adopta la forma de la función escalón

${\displaystyle F(t)=\{\begin{array}{l}{F}_{0}t\ge 0\\ 0t<0\end{array}}$

Resolvemos la ecución diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{F_0}{m}}$

Integración de la ecuación diferencial

La solución particular es

${\displaystyle \begin{array}{l}{x}_1=\text{cte}\\ {\omega }_0^2{x}_1=\frac{F_0}{m}\end{array}}$

La solución completa es la suma de la homogénea más la particular

${\displaystyle \begin{array}{l}x=\frac{F_0}{m{\omega }_0^2}+\exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle \begin{array}{l}\frac{dx}{dt}=-\gamma \exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)+\\ \omega \exp (-\gamma t)\left(A\cos (\omega t)-B\sin (\omega t)\right)\\ t=0\{\begin{array}{l}x=x_0\\ \frac{dx}{dt}=v_0\end{array}\\ x=\frac{F_0}{m{\omega }_0^2}+\exp (-\gamma t)\left(\left(\frac{v_0}{\omega }+\frac{\gamma }{\omega }\left(x_0-\frac{F_0}{m{\omega }_0^2}\right)\right)\sin (\omega t)+\left(x_0-\frac{F_0}{m{\omega }_0^2}\right)\cos (\omega t)\right)\end{array}}$

Para el caso de que las condiciones iniciales sean: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle x=\frac{F_0}{m{\omega }_0^2}\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\right)}$

Vamos a representar la función x(t) en función de ω₀t para un valor del coeficiente de rozamiento γ=ω₀·g. Escribimos la función x(t) de forma apropiada

${\displaystyle \begin{array}{l}x=\frac{F_0}{m{\omega }_0^2}\left(1-\exp (-g{\omega }_{0}t)\left(\frac{g}{\sqrt{1-g^2}}\sin \left(\sqrt{1-g^2}{\omega }_{0}t\right)+\cos \left(\sqrt{1-g^2}{\omega }_{0}t\right)\right)\right)\\ \gamma =g{\omega }_0\omega =\sqrt{1-g^2}{\omega }_0\end{array}}$

g=0.25;
t=linspace(0,15,100); %w0·t en el eje horizontal
w=sqrt(1-g^2);
x=1-exp(-g*t).*(g*sin(w*t)/w+cos(w*t));
plot(t,x,'r')
title('Escalón')
xlabel('\omega_0t')
ylabel('x(t)')
grid on

[xmax nmax]=max(abs(x));
fprintf('El máximo valor del desplazamiento es %1.5f 
en el instante %1.5f\n',xmax,t(nmax))

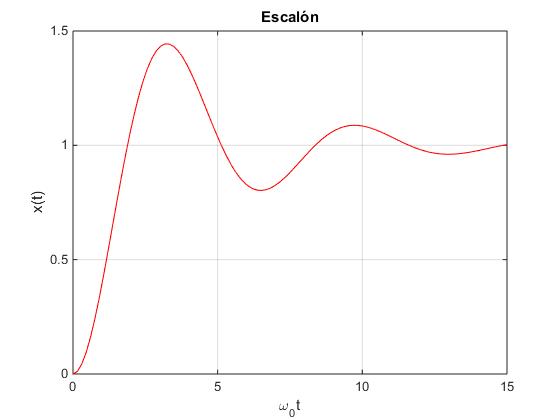
El máximo valor del desplazamiento es 1.44346 en el instante 3.18182

La función presenta un máximo pronunciado para t_p=π/ω, que obtenemos derivando x(t) e igualando a cero.

Por otra parte, la función x(t) tiende asintóticamente al valor

${\displaystyle \frac{F_0}{m{\omega }_0^2}}$

El primer máximo sobrepasa el valor final de x(t) en la cantidad

${\displaystyle \frac{F_0}{m{\omega }_0^2}\exp \left(-\frac{\gamma \pi }{\omega }\right)}$

Transformada de Laplace

Vamos a resolver la ecuación diferencial mediante la transformada de Laplace para una fuerza similar a la anterior pero más general. La definición de la fuerza aplicada al móvil es ahora

${\displaystyle F(t)=\{\begin{array}{l}{F}_{0}t\ge a\\ 0t<a\end{array}}$

Vamos a volver a obtener la expresión de x(t) utilizando la transformada de Laplace de la función escalón u(t-a) que es exp(-as)/s. La transformada de la función f(t)=F(t)/m es

${\displaystyle g(s)=\frac{F_0}{m}\frac{\exp (-as)}{s}}$

Tenemos que calcular la transformada inversa de Laplace x₁(t) de la expresión

${\displaystyle \frac{F_0}{m}\exp (-as)\frac{1}{s\left(s^2+2\gamma s+{\omega }_0^2\right)}}$

Descomponemos la fracción en suma de fracciones simples

${\displaystyle \begin{array}{l}\frac{1}{s\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{As+B}{s^2+2\gamma s+{\omega }_0^2}+\frac{C}{s}\\ C=\frac{1}{{\omega }_0^2}A=-\frac{1}{{\omega }_0^2}B=-\frac{2\gamma }{{\omega }_0^2}\\ \frac{1}{s\left(s^2+2\gamma s+{\omega }_0^2\right)}=\frac{1}{{\omega }_0^2}\left(\frac{1}{s}-\frac{s+2\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}\right)=\\ \frac{1}{{\omega }_0^2}\left(\frac{1}{s}-\frac{s+\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}-\frac{\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}\right)\end{array}}$

Examinando la tabla de las transformadas de Laplace obtenemos la expresión del primer término x₁(t) debido a la fuerza

${\displaystyle \begin{array}{l}\frac{F_0}{m{\omega }_0^2}\left(\begin{array}{l}\frac{\exp (-as)}{s}-\frac{s+\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}\exp (-as)\\ -\frac{\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_0^2-{\gamma }^2\right)}\exp (-as)\end{array}\right)\\ x_1(t)=\frac{F_0}{m{\omega }_0^2}\left(\begin{array}{l}1-\exp \left(-\gamma (t-a)\right)\cos \left(\omega (t-a)\right)-\\ \frac{\gamma }{\omega }\exp \left(-\gamma (t-a)\right)\sin \left(\omega (t-a)\right)\end{array}\right)u(t-a)\end{array}}$

La solución completa es x(t)=x₁(t)+x₂(t)

${\displaystyle \begin{array}{l}x(t)=\exp (-\gamma t)\left(x_0\cos (\omega t)+\frac{\left(\gamma x_0+v_0\right)}{\omega }\sin (\omega t)\right)\\ +\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\right)u(t-a)\end{array}}$

Para el caso de que las condiciones iniciales sean: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle x(t)=\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\right)u(t-a)}$

Esta es la respuesta x(t) a la acción de la fuerza F(t) que utilizaremos en los siguientes apartados.

Cuando a=0 como en el apartado anterior y para t≥0

${\displaystyle \begin{array}{l}x(t)=\exp (-\gamma t)\left(x_0\cos (\omega t)+\frac{\left(\gamma x_0+v_0\right)}{\omega }\sin (\omega t)\right)\\ +\frac{F_0}{m{\omega }_0^2}\left(u(t)-\exp \left(-\gamma t\right)\left(\cos \left(\omega t\right)+\frac{\gamma }{\omega }\sin \left(\omega t\right)\right)\right)\end{array}}$

Si la posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle x(t)=\frac{F_0}{m{\omega }_0^2}\left(1-\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\right)}$

La misma expresión que hemos obtenido anteriormente

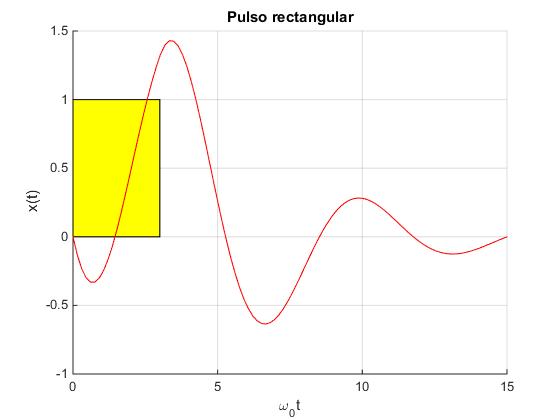
Pulso rectangular (superposición)

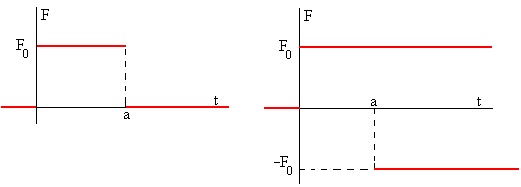
La definición de la función F(t) es

${\displaystyle F(t)=\{\begin{array}{l}{F}_{0}0\le t<a\\ 0t\ge a\end{array}}$

Como vemos en la figura de la derecha el pulso rectangular es la suma de dos funciones escalón

${\displaystyle F_1(t)=\{\begin{array}{l}{F}_{0}t\ge 0\\ 0t<0\end{array}{F}_2(t)=\{\begin{array}{l}-F_{0}t\ge a\\ 0t<a\end{array}}$

Aplicando el principio de superposición, el término x₁(t)=x₁₁(t)+x₁₂(t) es la suma de dos términos debidos a cada una de las dos fuerzas: la fuerza F₁(t)

• Para t>0

${\displaystyle x_{11}(t)=\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma t\right)\left(\cos \left(\omega t\right)+\frac{\gamma }{\omega }\sin \left(\omega t\right)\right)\right)u(t)}$

y la fuerza F₂(t) ${\displaystyle }$

• Para t≥a

${\displaystyle x_{12}(t)=-\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\right)u(t-a)}$

La solución completa es x(t)=x₁(t)+x₂(t)

${\displaystyle \begin{array}{l}x(t)=\exp (-\gamma t)\left(x_0\cos (\omega t)+\frac{\left(\gamma x_0+v_0\right)}{\omega }\sin (\omega t)\right)\\ +\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma t\right)\left(\cos \left(\omega t\right)+\frac{\gamma }{\omega }\sin \left(\omega t\right)\right)\right)u(t)\\ -\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\right)u(t-a)\end{array}}$

Se sugiere al lector modificar los valores del amortiguamiento g<1, la anchura del pulso a y las condiciones iniciales: posición inicial x₀ y velocidad inicial v₀

Expresamos en MATLAB la función u(t-a) como una comparación (t≥a) que devuelve 1 si es cierto y cero si es falso.

g=0.25; %rozamiento
x0=0; %condiciones iniciales
v0=-1;
t=linspace(0,15,100); %w0·t en el eje horizontal
w=sqrt(1-g^2);
a=3; %anchura del pulso rectangular
%respuesta a la función escalón
f0=@(t) exp(-g*t).*(x0*cos(w*t)+(g*x0+v0)*sin(w*t)/w);
f=@(t,a) (t>=a)-exp(-g*(t-a)).*(g*sin(w*(t-a))/w+cos(w*(t-a)));
hold on
%Pulso
xx=[0 a a 0];
yy=[1 1 0 0];
fill(xx,yy,'y'); %rellena un área de color especificado
%respuesta
t1=t(t<a); x1=f0(t1)+f(t1,0);
t2=t(t>=a); x2=f0(t2)+f(t2,0)-f(t2,a);
x=[x1 x2];
plot(t,x,'r')

title('Pulso rectangular')
xlabel('\omega_0t')
ylabel('x(t)')
grid on
hold off

Para el caso de que las condiciones iniciales sean: posición inicial x₀=0 y velocidad inicial v₀=0 en el instante t=0.

${\displaystyle \begin{array}{l}x(t)=\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma t\right)\left(\cos \left(\omega t\right)+\frac{\gamma }{\omega }\sin \left(\omega t\right)\right)\right)u(t)\\ -\frac{F_0}{m{\omega }_0^2}\left(1-\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\right)u(t-a)\end{array}}$

Como en la sección anterior, representamos la función x(t) en función de ω₀t para un valor del coeficiente de rozamiento γ=ω₀·g, para ello escribimos la función x(t) de forma apropiada, poniendo

${\displaystyle \gamma =g{\omega }_0\omega =\sqrt{1-g^2}{\omega }_0}$

Nos queda por demostar que cuando a es muy pequeño y F₀ es grande se obtiene la misma expresión para x(t) que hemos obtenido para el pulso delta de Dirac

${\displaystyle x(t)=\frac{I_0}{m\omega }\exp (-\gamma t)\sin (\omega t)}$

donde el impulso I₀ es igual al producto de la fuerza F₀ por el tiempo que actúa a. I₀=F₀·a

Utilizamos MATLAB para calcular el límite de la expresión entre paréntesis de x(t)

${\displaystyle \begin{array}{l}x(t)=\frac{F_{0}a}{m{\omega }_0^2}\frac{f(a)}{a}=\frac{I_0}{m{\omega }_0^2}\frac{f(a)}{a}\\ f(a)=-\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\\ +\exp \left(-\gamma (t-a)\right)\left(\cos \left(\omega (t-a)\right)+\frac{\gamma }{\omega }\sin \left(\omega (t-a)\right)\right)\\ \underset{a\to 0}{\lim }\frac{f(a)}{a}=\underset{a\to 0}{\lim }f\text{'}(a)\end{array}}$

Este límite es del tipo 0/0 que se puede resolver aplicando La regla de L'Hôpital.

>> syms g t w a;
>> x=-exp(-g*t)*(cos(w*t)+g*sin(w*t)/w)
+exp(-g*(t-a))*(cos(w*(t-a))+g*sin(w*(t-a))/w);
>> limit(x/a,a,0)
ans =(sin(t*w)*(g^2 + w^2))/(w*exp(g*t))

El límite vale

${\displaystyle \frac{{\omega }^2+{\gamma }^2}{\omega }\sin (\omega t)\exp (-\gamma t)=\frac{{\omega }_0^2}{\omega }\sin (\omega t)\exp (-\gamma t)}$

Por lo que

${\displaystyle x(t)=\frac{I_0}{m\omega }\exp (-\gamma t)\sin (\omega t)}$

que es el mismo resultado que obtuvimos con la función delta de Dirac

Actividades

Se introduce

• la posición inicial x₀, en el control titulado Posición inicial
• la velocidad inicial del móvil v₀, en el control titulado Velocidad inicial.
• la constante de amortiguamiento γ, en el control titulado Amortiguamiento
• El tiempo de duración de la fuerza oscilante, en el control titulado Tiempo fuerza
• La frecuencia angular natural ω₀=1 del oscilador se ha fijado en 1 rad/s
• El cociente F₀/m=1 se ha fijado en el programa interactivo

Se pulsa en el botón Nuevo.

Probar con otras condiciones iniciales distintas de x₀=0 y v₀=0. Por ejemplo, x₀=1 y v₀=0, x₀=0 y v₀=-1.