Otros péndulos compuestos

En este apartado describimos péndulos compuestos interesantes

Varilla con masa puntual

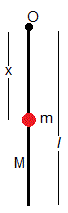
El péndulo compuesto está formado por una varilla delgada de masa M y longitud l y una bola de pequeño diámetro de masa m que puede sujetarse a la varilla a una distancia x de su extremo O. El péndulo oscila alrededor de un eje perpendicular a la pantalla y que pasa por O

Vamos a determinar el periodo de las oscilaciones de pequeña amplitud

${\displaystyle P=2\pi \sqrt{\frac{I_O}{(m+M)g{x}_{cm}}}}$

Donde I_O es el momento de inercia del péndulo y x_cm es la posición del centro de masa medida desde O

${\displaystyle \begin{array}{l}{I}_O=\left(\frac{1}{12}M{l}^2+M{\left(\frac{l}{2}\right)}^2\right)+m{x}^2=\frac{1}{3}M{l}^2+m{x}^2\\ x_{cm}=\frac{M\frac{l}{2}+mx}{M+m}\\ P^2=\frac{4{\pi }^2}{g}\frac{\frac{1}{3}M{l}^2+m{x}^2}{M\frac{l}{2}+mx}\end{array}}$

Calculamos el mínimo del periodo P o de P²

${\displaystyle \begin{array}{l}\frac{d{P}^2}{dx}=0\\ m{x}^2+Mlx-\frac{1}{3}M{l}^2=0\\ \frac{x}{l}=\frac{-M\pm \sqrt{M^2+\frac{4}{3}mM}}{2m}\end{array}}$

Solamente es posible la raíz positiva

${\displaystyle \frac{x_m}{l}=\frac{\sqrt{1+\frac{4}{3}\frac{m}{M}}-1}{2\frac{m}{M}}}$

Expresamos el periodo en términos de las magnitudes adimensionales x/l y m/M

${\displaystyle P=2\pi \sqrt{\frac{l}{g}}\sqrt{\frac{\frac{1}{3}+\frac{m}{M}{\left(\frac{x}{l}\right)}^2}{\frac{1}{2}+\frac{m}{M}\frac{x}{l}}}}$

El periodo del péndulo compuesto es proporcional al periodo de un péndulo simple P₀ de longitud l. Representamos la función P/P₀ para cuatro valores del cociente m/M=0.5, 1, 1.5, 2

hold on 
for mu=0.5:0.5:2 %cociente m/M
    f=@(x) sqrt((1/3+mu*x.^2)./(1/2+mu*x));
    fplot(f,[0,1])
    x_m=(-1+sqrt(1+4*mu/3))/(2*mu);
    plot(x_m,f(x_m),'ro','markersize',3,'markerfacecolor','r')
end
hold off
grid on
xlabel('x/l')
ylabel('P/P_0')
title('Periodo de un péndulo compuesto')

Un punto de color rojo, señala la posición del mínimo x_m del periodo

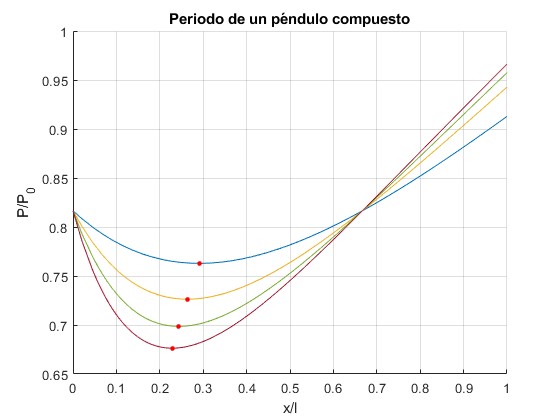
Observamos otra particularidad, el periodo del péndulo compuesto cuando x=0 (solamente la varilla)

${\displaystyle P=2\pi \sqrt{\frac{\frac{1}{3}M{l}^2}{g·M\frac{l}{2}}}=2\pi \sqrt{\frac{2}{3}\frac{l}{g}}}$

es igual al periodo del péndulo cuando la bola está situada a una distancia x/l=2/3 de O

${\displaystyle P=2\pi \sqrt{\frac{\frac{1}{3}M{l}^2+m{\left(\frac{2l}{3}\right)}^2}{g\left(M\frac{l}{2}+m\frac{2l}{3}\right)}}=2\pi \sqrt{\frac{2}{3}\frac{l}{g}}}$

Placa rectangular delgada

Consideremos una placa rectangular de masa M y lados a y b.

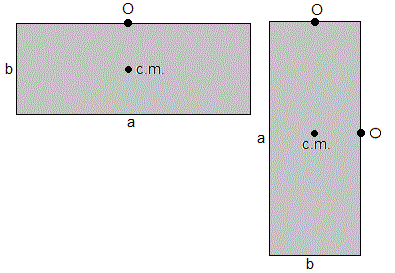
Hacemos oscilar a la placa alrededor de un eje perpendicular y que pasa por O. El periodo del péndulo compuesto para oscilaciones de pequeña amplitud es

${\displaystyle P=2\pi \sqrt{\frac{I_O}{Mg{x}_{cm}}}}$

• En la situación a la izquierda de la figura

${\displaystyle \begin{array}{l}{I}_O=\frac{1}{12}M\left(a^2+b^2\right)+M{\left(\frac{b}{2}\right)}^2=\frac{1}{12}M{a}^2+\frac{1}{3}M{b}^2\\ x_{cm}=\frac{b}{2}\\ P_1=2\pi \sqrt{\frac{\frac{1}{12}M{a}^2+\frac{1}{3}M{b}^2}{Mg\frac{b}{2}}}=2\pi \sqrt{\frac{a}{g}}\sqrt{\frac{1+4\frac{b^2}{a^2}}{6\frac{b}{a}}}=P_0\sqrt{\frac{1+4r^2}{6r}}\end{array}}$

• En la situación a la derecha de la figura

${\displaystyle \begin{array}{l}{I}_O=\frac{1}{12}M\left(a^2+b^2\right)+M{\left(\frac{a}{2}\right)}^2=\frac{1}{3}M{a}^2+\frac{1}{12}M{b}^2\\ x_{cm}=\frac{a}{2}\\ P_2=2\pi \sqrt{\frac{\frac{1}{3}M{a}^2+\frac{1}{12}M{b}^2}{Mg\frac{a}{2}}}=2\pi \sqrt{\frac{a}{g}}\sqrt{\frac{4+\frac{b^2}{a^2}}{6}}=P_0\sqrt{\frac{4+r^2}{6}}\end{array}}$

Los periodos son iguales cuando la placa es cuadrada b=a, pero hay otras posibilidades.

Representamos gráficamente P₁/P₀ y P₂/P₀ en función de r=b/a entre 0.1 y 3.

hold on
f=@(x) sqrt((1+4*x.^2)./(6*x));
fplot(f,[0.1,3])
f=@(x) sqrt((4+x.^2)./6);
fplot(f,[0.1,3])
x1=(3+sqrt(5))/2;
plot(x1,f(x1),'ro','markersize',3,'markerfacecolor','r')
x1=(3-sqrt(5))/2;
plot(x1,f(x1),'ro','markersize',3,'markerfacecolor','r')
plot(1,f(1),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('b/a')
legend('1','2','Location','best')
ylabel('P/P_0')
title('Placa rectangular')

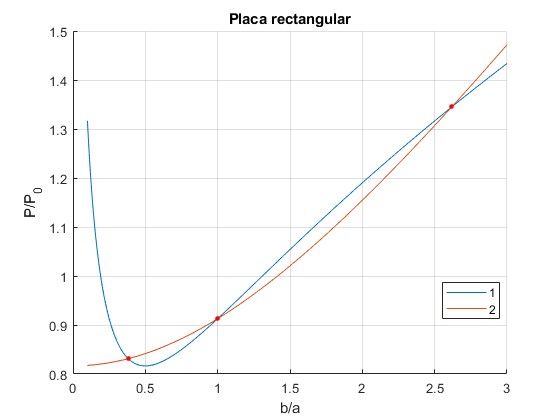
Observamos que el periodo P₁ tiene un mínimo en r=b/a=0.5, que se obtiene derivando P₁ o su cuadrado con respecto de r

${\displaystyle \begin{array}{l}\frac{d{P}_1^2}{dr}=0\\ 48r^2-6\left(4r^2+1\right)=0\\ r_m=\frac{1}{2}\end{array}}$

Los periodos son iguales, P₁=P₂

${\displaystyle \begin{array}{l}\frac{1+4r^2}{6r}=\frac{4+r^2}{6}\\ r^3-4r^2+4r-1=0\end{array}}$

Una de las raíces r=1 cuando b=a (placa cuadrada), pero hay otros dos valores

${\displaystyle \begin{array}{l}{r}^3-4r^2+4r-1=(r-1)\left(r^2-3r+1\right)=0\\ r=\frac{3\pm \sqrt{9-4}}{2}=\frac{3\pm \sqrt{5}}{2}\end{array}}$

Las tres raíces se señalan mediante puntos de color rojo en la figura

Péndulo compuesto no homogéneo

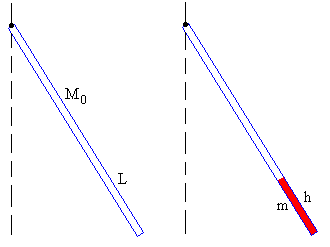
Consideremos un péndulo compuesto formado por un tubo hueco largo y de pequeño radio de masa M₀ y longitud L como se muestra en la figura. Se sujeta por un eje que pasa por uno de los extremos y se desplaza de la  posición de equilibrio comenzando a oscilar. El periodo es

${\displaystyle P_0=2\pi \sqrt{\frac{I_0}{M_{0}g{y}_0}}}$

Siendo I₀=M₀L²/3 el momento de inercia y y₀=L/2 la posición del centro de masa

${\displaystyle P_0=2\pi \sqrt{\frac{2L}{3g}}}$

Supongamos que el tubo hueco se rellena uniformemente hasta una altura h con una masa m de cierta sustancia (en color rojo). El periodo es

${\displaystyle P=2\pi \sqrt{\frac{I_0+I_m}{(M_0+m)gy}}}$

Donde I_m es el momento de inercia de la masa m alrededor del eje de oscilación e y es la distancia del centro de masa del sistema formado por el tubo y la masa m de relleno desde el centro de oscilación.

${\displaystyle \begin{array}{l}y=\frac{M_0(L/2)+m(L-h/2)}{M_0+m}\\ I_m=\frac{1}{12}m{h}^2+m{\left(L-\frac{h}{2}\right)}^2\end{array}}$

El periodo P vale

${\displaystyle P=2\pi \sqrt{\frac{M_0\frac{L^2}{3}+m{L}^2-mLh+m\frac{h^2}{3}}{g\left(M_0\frac{L}{2}+mL-m\frac{h}{2}\right)}}}$

Sea M la masa de la sustancia que rellena completamente el tubo, entonces cuando el tubo está parcialmente lleno hasta una altura h,  m=M·h/L. El periodo P se expresa

${\displaystyle P=2\pi \sqrt{\frac{2L}{3g}}\sqrt{\frac{1+3\frac{M}{M_0}\left(\frac{h}{L}\right)-3\frac{M}{M_0}{\left(\frac{h}{L}\right)}^2+\frac{M}{M_0}{\left(\frac{h}{L}\right)}^3}{1+2\frac{M}{M_0}\left(\frac{h}{L}\right)-\frac{M}{M_0}{\left(\frac{h}{L}\right)}^2}}}$

El periodo P es función de los cocientes R=M/M₀ y x=h/L

${\displaystyle P=2\pi \sqrt{\frac{2L}{3g}}\sqrt{\frac{1+3Rx-3R{x}^2+R{x}^3}{1+2Rx-R{x}^2}}}$

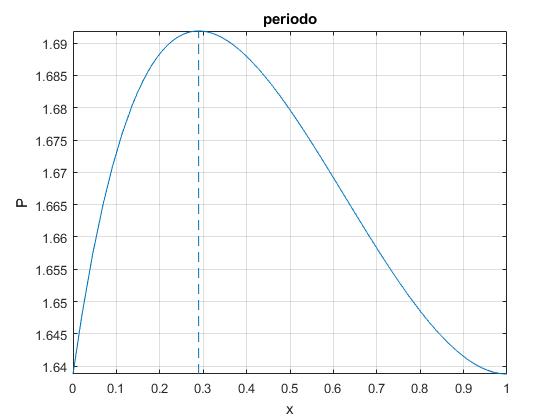
El periodo P presenta un máximo para cierto valor de x=h/L, que se calcula igualando la derivada primera de P respecto de x, a cero, dP/dx=0. Resultando la ecuación

R²x⁴-4R²x³+3R²x²-3Rx²+4Rx-R=0

Ejemplo

Sea un tubo vacío de longitud L=1 m y de masa M₀=0.1402 kg. El periodo de este péndulo es 1.64 s. Se rellena completamente el tubo con madera cuya masa M=0.0816 kg, de modo que R=M/M₀=0.582, el periodo es el mismo. El máximo periodo es 1.69 s, se obtiene cuando la longitud de la pieza de madera que rellena parcialmente el tubo es 0.289L

R=0.58; %cociente M/M0
L=1; %longitud
f=@(x) 2*pi*sqrt(2*L/(3*9.8))*sqrt((1+3*R*x-3*R*x.^2+R*x.^3)
./(1+2*R*x-R*x.^2));
fplot(f,[0,1])
r=roots([1,-4,3*(1-1/R), 4/R,-1/R]);
xMax=0;
for i=1:length(r)
    if r(i)>0 && r(i)<1-0.001
       xMax=r(i);
       break;
    end
end
line([xMax,xMax],[f(0),f(xMax)],'lineStyle','--')
grid on
xlabel('x')
ylabel('P')
title('periodo')

>> xMax
xMax =    0.2894
>> f(xMax)
ans =    1.6919

Péndulo simple, péndulo compuesto

En el laboratorio utilizamos una cuerda sujeta por un extremo y por el otro, unida a una esfera acero inoxidable de pequeño radio como modelo de péndulo simple para calcular la aceleración de la gravedad. En este apartado, se compara el periodo de un péndulo compuesto que consta de una varilla de longitud L unida a una esfera de radio R con el periodo de un péndulo simple de longitud L+R

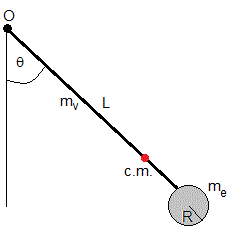
Sea el péndulo compuesto que consta de una varilla de longitud L que puede girar sin rozamiento por el extremo O y por el otro, está unida a una esfera de radio R

La densidad de la varilla es ρ_v, la sección es circular de radio r, su masa es m_v=ρ_v(πr²L)

La densidad de la esfera ρ, su masa m_e=ρ(4πr³/3)

El periodo de las oscilaciones de un péndulo compuesto en la aproximación de amplitud pequeña es

${\displaystyle P_c=2\pi \sqrt{\frac{I_O}{mgb}}}$

donde m=m_v+m_e. El periodo de un péndulo simple de la misma longitud l=L+R es

${\displaystyle P_s=2\pi \sqrt{\frac{L+R}{g}}}$

El momento de inercia vale

${\displaystyle \begin{array}{l}{I}_O=\frac{1}{3}{m}_v{L}^2+\left(\frac{2}{5}{R}^2+{\left(L+R\right)}^2\right)m_e\\ I_O=\frac{1}{3}\lambda L^3+\left(\frac{2}{5}{R}^2+{\left(L+R\right)}^2\right)\rho \frac{4}{3}\pi R^3,\lambda ={\rho }_v\pi r^2\end{array}}$

λ es la densidad lineal de la varilla

La distancia b del centro de masa al punto de suspensión O es

${\displaystyle b=\frac{m_v\frac{L}{2}+m_e\left(L+R\right)}{m_v+m_e}=\frac{\lambda \frac{L^2}{2}+\rho \frac{4}{3}\pi R^3\left(L+R\right)}{m_v+m_e}}$

El periodo del péndulo compuesto es

${\displaystyle P_c=\frac{2\pi }{\sqrt{g}}\sqrt{\frac{\frac{1}{3}\lambda L^3+\left(\frac{2}{5}{R}^2+{\left(L+R\right)}^2\right)\rho \frac{4}{3}\pi R^3}{\lambda \frac{L^2}{2}+\rho \frac{4}{3}\pi R^3\left(L+R\right)}}}$

Vamos a determinar la longitud de la varilla L, que hace que el periodo del péndulo simple de longitud L+R se igual al periodo de este péndulo compuesto, P_s=P_c

${\displaystyle \frac{4{\pi }^2}{g}\left(L+R\right)=\frac{4{\pi }^2}{g}\frac{\frac{1}{3}\lambda L^3+\left(\frac{2}{5}{R}^2+{\left(L+R\right)}^2\right)\rho \frac{4}{3}\pi R^3}{\lambda \frac{L^2}{2}+\rho \frac{4}{3}\pi R^3\left(L+R\right)}}$

Simplificamos y llegamos a una ecuación cúbica en L

${\displaystyle L^3-3R{L}^2-\frac{16\pi }{5}{R}^5\frac{\rho }{\lambda }=\mathrm{0,}\{\begin{array}{l}a=3R\\ b=0\\ c=-\frac{16\pi }{5}{R}^5\frac{\rho }{\lambda }\end{array}}$

La ecuación cúbica puede tener tres raíces reales o una real y dos complejas conjugadas, dependiendo de Q y K

${\displaystyle Q=\frac{a^2-3b}{9}=R^{2}K=\frac{2a^3-9ab+27c}{54}=R^3+\frac{c}{2}}$

La condición para que tenga una única raíz real es

${\displaystyle \begin{array}{l}{K}^2>Q^3\\ {\left(R^3+\frac{c}{2}\right)}^2>R^6\end{array}}$

Como c es un número negativo

${\displaystyle \begin{array}{l}{R}^3+\frac{c}{4}<0\\ R^3-\frac{4\pi }{5}{R}^5\frac{\rho }{\lambda }<0\\ \frac{4\pi }{5}{R}^2\frac{\rho }{\lambda }>1\\ \frac{4}{5}\left(\frac{R^2}{r^2}\right)>\frac{{\rho }_v}{\rho }\end{array}}$

Recordamos que R es el radio de la esfera y ρ su densidad. r es el radio de la sección de la varilla y ρ_v su densidad

Consideremos una experiencia de laboratorio de medida del periodo de las oscilaciones para pequeñas amplitudes

• Hilo de algodón, densidad ρ_v=1.54 g/cm³, sección circular de radio r=0.5 mm
• Esfera de acero inoxidable de densidad ρ=7.96 g/cm³ y radio R=1 cm

Este péndulo cumple sobradamente la condición

${\displaystyle \frac{4}{5}\left(\frac{R^2}{r^2}\right)>\frac{{\rho }_v}{\rho }}$

320>0.1935

El cociente

${\displaystyle \frac{P_c}{P_s}=\frac{\sqrt{\frac{\frac{1}{3}\lambda L^3+\left(\frac{2}{5}{R}^2+{\left(L+R\right)}^2\right)\rho \frac{4}{3}\pi R^3}{\lambda \frac{L^2}{2}+\rho \frac{4}{3}\pi R^3\left(L+R\right)}}}{\sqrt{L+R}}}$

Para L=0

${\displaystyle \frac{P_c}{P_s}=\sqrt{\frac{7}{5}}}$

Cuando la longitud del hilo se hace grande L→∞

${\displaystyle \begin{array}{l}\frac{P_c}{P_s}=\sqrt{\frac{\frac{1}{3}\lambda +\left(\frac{2}{5}\frac{R^2}{L^3}+\frac{{\left(L+R\right)}^2}{L^3}\right)\rho \frac{4}{3}\pi R^3}{\frac{L+R}{L}\left(\frac{1}{2}\lambda +\rho \frac{4}{3}\pi R^3\frac{L+R}{L^2}\right)}}\\ \underset{L\to \infty }{\lim }\frac{P_c}{P_s}=\sqrt{\frac{2}{3}}\end{array}}$

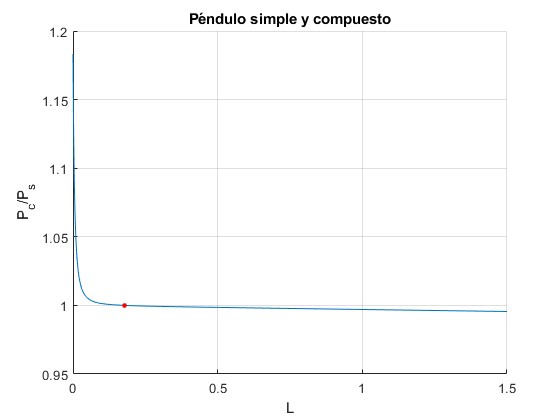
Representamos el cociente P_c/P_s en función de L, señalando el valor L que hace que ambos periodos sean iguales L=0.1782, la raíz real de la ecuación cúbica

function simple_compuesto
    rho=7960; %densidad de la esfera
    R=0.01; %radio de la esfera
    rho_v=1540; %densidad del algodón
    r=0.5e-3; %radio de la varilla
    lambda=pi*r^2*rho_v;
    c=-16*pi*R^5*rho/(5*lambda);
    raiz=raices_3([1,3*R,0,c]);
    disp(real(raiz(1)))
    P=@(x) sqrt((lambda*x.^3/3+(2*R^2/5+(x+R).^2)*rho*4*pi*R^3/3)./
(lambda*x.^2/2+rho*4*pi*R^3*(x+R)/3))./sqrt(x+R);
    hold on
    fplot(P,[0,1.5])
    plot(real(raiz(1)),1,'ro','markersize',3,'markerfacecolor','r')
    hold off
    grid on
    xlabel('L')
    ylabel('P_c/P_s')
    title('Péndulo simple y compuesto')
    
    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        K=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if K^2<Q^3
            tetha=acos(K/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(K)*nthroot(abs(K)+sqrt(K^2-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

   0.1782

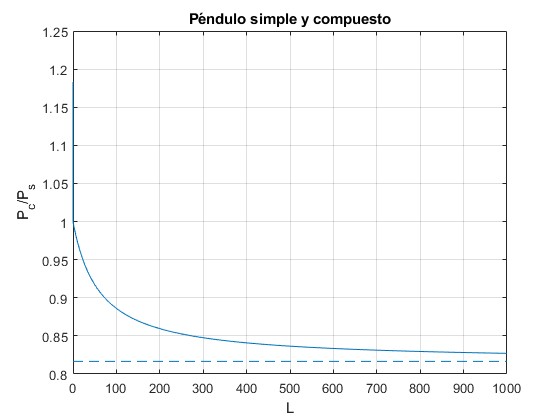
En esta otra gráfica, observamos el caso habitual, la longitud L de la varilla es mucho mayor que el radio de la esfera R, entonces $\frac{P_c}{P_s}\to \sqrt{\frac{2}{3}}$

    rho=7960; %densidad de la esfera
    R=0.01; %radio de la esfera
    rho_v=1540; %densidad del algodón
    r=0.5e-3; %radio de la varilla
    lambda=pi*r^2*rho_v;
    c=-16*pi*R^5*rho/(5*lambda);
    raiz=raices_3([1,3*R,0,c]);
    disp(real(raiz(1)))
    P=@(x) sqrt((lambda*x.^3/3+(2*R^2/5+(x+R).^2)*rho*4*pi*R^3/3)./
(lambda*x.^2/2+rho*4*pi*R^3*(x+R)/3))./sqrt(x+R);
    fplot(P,[0,1000])
    line([0,1000],[sqrt(2/3),sqrt(2/3)],'lineStyle','--')
    grid on
    ylim([0.8,1.25])
    xlabel('L')
    ylabel('P_c/P_s')
    title('Péndulo simple y compuesto')

Referencias

Kettler J. E. A variable mass physical pendulum, Am. J. Phys. 63 (11) November 1995, pp. 1049-1051

Tim H Richardson, Stuart A Brittle. Physical pendulum experiments to enhance the understanding of moments of inertia and simple harmonic motion. Physics Education, 47 (5) 2012, pp. 537-544

Ira M. Freeman. Rectangular plate pendulum Am. J. Phys. 22 (4) April 1954, pp. 157-158

E L Fulton, T J Gay. Does a physical pendulum ever act like a simple pendulum?. Eur. J. Phys. 45 (2024) 025001