El péndulo interrumpido

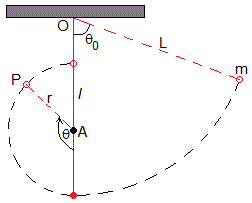
Consideremos un péndulo simple, que consiste en una masa puntual m conectada mediante un hilo inextensible de longitud L a un punto fijo O que consideramos el origen.

Debajo del origen a una distancia l<L hay una aguja A clavada perpendicular al plano del movimiento del péndulo, cuyo diámetro es muy pequeño.

Supongamos que el péndulo se desvía un ángulo θ₀ y se suelta. Describe un arco de circunferencia de radio L, cuando llega a la parte más baja de la trayectoria, el hilo choca con el obstáculo A, hace que esta trayectoria se interrumpa y la masa puntual describa un arco de circunferencia de radio r=L-l, tal como se muestra en la figura.

Aplicamos el principio de conservación de la energía entre la posición inicial, cuando el péndulo se ha desviado un ángulo θ₀, y la final, cuando la masa puntual se encuentra en P cuya posición angular es θ.

Tomamos el nivel cero de la energía potencial en el punto de suspensión O

$\begin{array}{l} \frac{1}{2} m v^{2} - m g (l - r \cos (π - θ)) = - m g L \cos θ_{0} \\ v^{2} = 2 g (l + r \cos θ - L \cos θ_{0}) \end{array}$

Fijamos la posición del obstáculo A

La partícula describe un arco de circunferencia vertical de radio r=L-l y centro en el obstáculo A

Oscilaciones, la posición final es θ₁<π/2

La velocidad final se anula para θ<π/2

$\begin{array}{l} l + r \cos θ_{1} - L \cos θ_{0} = 0 \\ \cos θ_{1} = \frac{L \cos θ_{0} - l}{L - l} \end{array}$

El péndulo vuelve hacia atrás y oscila con amplitudes θ₀ y θ₁

El valor límite de θ₀ para este caso, se obtiene poniendo θ₁=π/2. Para que el movimiento oscilatorio se produzca se tiene que cumplir que

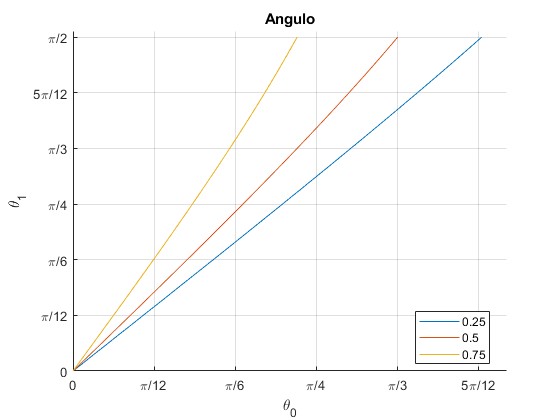
$\begin{array}{l} L \cos θ_{0} - l = 0, \\ θ_{0} \leq \arccos (\frac{l}{L}) \end{array}$

Representamos θ₁ en función de θ₀ para tres valores de la posición del obstáculo l/L=0.25, 0.5 y 0.75

hold on
for r=[0.25,0.5,0.75]
    th_lim=acos(r);
    fplot(@(x) acos((cos(x)-r)/(1-r)), [0,th_lim],'displayName',num2str(r))
end
hold off
grid on
legend('-DynamicLegend','location','best')
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_0')
ylabel('\theta_1')
title('Angulo')

El periodo es la suma de dos semiperiodos, de un péndulo de longitud L y amplitud θ₀ y de otro péndulo de longitud L-l y amplitud θ₁.

Cuando los ángulos θ₀ y θ₁ son pequeños

$P = \frac{1}{2} (P_{1} + P_{2}) = π (\sqrt{\frac{L}{g}} + \sqrt{\frac{L - l}{g}})$

Cuando la amplitud de las oscilaciones es grande el periodo es

$\begin{array}{l} P = 2 \sqrt{\frac{L}{g}} K (k_{1}) + 2 \sqrt{\frac{L - l}{g}} K (k_{2}), k_{1} = \sin \frac{θ_{0}}{2}, k_{2} = \sin \frac{θ_{1}}{2} \\ \cos θ_{1} = \frac{L \cos θ_{0} - l}{L - l} \end{array}$

Sea el ángulo inicial θ=π/3 (60°), la longitud del péndulo L=1 m, la posición del obstáculo l=0.4 m, lo que asegura que θ₁<π/2 (90°)

th_0=pi/3;
L=1; %longitud del péndulo
l=0.4; %posición del obstáculo
th_1=acos((L*cos(th_0)-l)/(L-l));
P=2*sqrt(L/9.8)*ellipke(sin(th_0/2)^2)+2*sqrt((L-l)/9.8)*ellipke(sin(th_1/2)^2);
disp(P)

1.9624
>> pi*sqrt(L/9.8)+pi*sqrt((L-l)/9.8)
ans =    1.7809

El periodo exacto, 1.9624 s, difiere del que se obtiene a partir de la aproximación de oscilaciones de pequeña amplitud, 1.7809 s.

Dado que θ₁>θ₀, la utilidad de la aproximación es más difícil de justificar

Representamos el periodo P en función de θ₀ para un péndulo de longitud L=1 m, para tres valores de la posición del obstáculo l=0.25, 0.5 y 0.75

hold on
for r=[0.25,0.5,0.75]
    th_lim=acos(r);
    th_1=@(x) acos((cos(x)-r)/(1-r));
    f=@(x) 2*sqrt(1/9.8)*ellipke(sin(x/2).^2)+2*sqrt((1-r)/9.8)*
ellipke(sin(th_1(x)/2).^2);  
    fplot(f, [0,th_lim])
    P=pi*(sqrt(1/9.8)+sqrt((1-r)/9.8));
    line([0,5*pi/12],[P,P],'lineStyle','--')%aproximación
end
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_0')
ylabel('P (s)')
title('Periodo')

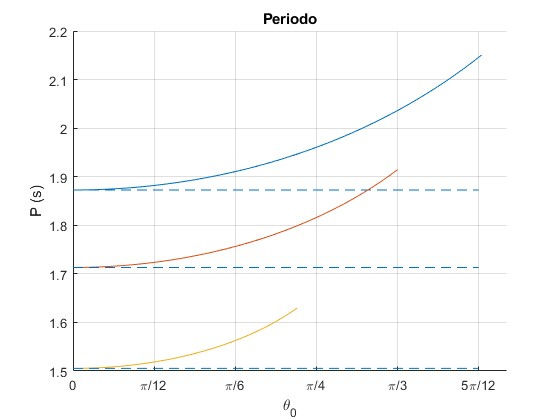
Las líneas a trazos es la aproximación para las oscilaciones de pequeña amplitud

Tensión del hilo nula, tiro parabólico

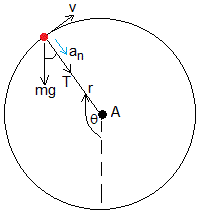
La partícula describe un arco de circunferencia vertical de ángulo θ₁ seguido de una trayectoria parabólica

Cuando θ₀>arccos(l/L), entonces θ₁>π/2

Calculamos la tensión del hilo cuando la partícula describe un arco de coircunferencia de centro A y radio r=L-l

Aplicamos la ecuación de la dinámica del movimiento circular uniforme

$T + m g \cos (π - θ) = m \frac{v^{2}}{r}$

La tensión del hilo T se anula para cuando

$\begin{array}{l} - m g \cos θ_{2} = m \frac{v_{2}^{2}}{r} \\ v_{2}^{2} = - r g \cos θ_{2}, θ_{2} > \frac{π}{2} \end{array}$

Aplicamos el principio de conservación de la energía para calcular v₂

$\begin{array}{l} - r g \cos θ_{2} = 2 g (l + r \cos θ_{2} - L \cos θ_{0}) \\ \cos θ_{2} = \frac{2}{3} \frac{L \cos θ_{0} - l}{L - l} \end{array}$

A partir de esta posición angular, la partícula describe una trayectoria parabólica

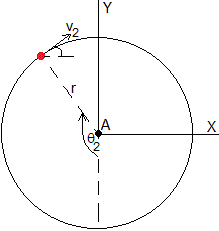
Situamos el origen en la posición del obstáculo A, y los ejes como se indica en la figura. La posición de partida de la partícula es

${\begin{cases} x_{0} = - r \sin (π - θ_{2}) \\ y_{0} = r \cos (π - θ_{2}) \end{cases}$

Las componentes v_x y v_y de la velocidad

${\begin{cases} v_{x} = v_{2} \cos (π - θ_{2}) \\ v_{y} = v_{2} \sin (π - θ_{2}) - g t \end{cases}$

La ecuación de la trayectoria es

$\begin{array}{l} {\begin{cases} x = - r \sin (π - θ_{2}) + v_{2} \cos (π - θ_{2}) \cdot t \\ y = r \cos (π - θ_{2}) + v_{2} \sin (π - θ_{2}) \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ {\begin{cases} x = - r \sin θ_{2} - v_{2} \cos θ_{2} \cdot t \\ y = - r \cos θ_{2} + v_{2} \sin θ_{2} \cdot t - \frac{1}{2} g t^{2} \end{cases} \end{array}$

Alcanza la altura máxima cuando v_y=0

$\begin{array}{l} t = \frac{v_{2} \sin θ_{2}}{g} \\ {\begin{cases} x_{m} = - r \sin θ_{2} - \frac{v_{2}^{2} \sin θ_{2} \cos θ_{2}}{g} = - (L - l) \sin^{3} θ_{2} \\ y_{m} = - r \cos θ_{2} + \frac{v_{2}^{2} \sin^{2} θ_{2}}{2 g} = - (L - l) \cos θ_{2} (1 + \frac{1}{2} \sin^{2} θ_{2}) \end{cases} \end{array}$

Se puede demostrar que la partícula atada al hilo pasa por el punto más alto de la trayectoria parabólica, es decir,

$\begin{array}{l} x_{m}^{2} + y_{m}^{2} < r^{2} \\ r^{2} {(1 - \cos^{2} θ_{2})}^{3} + \frac{r^{2}}{4} \cos^{2} θ_{2} {(3 - \cos^{2} θ_{2})}^{2} < r^{2} \\ 1 - \frac{3}{4} \cos^{6} θ_{2} + \frac{3}{2} \cos^{4} θ_{2} - \frac{3}{4} \cos^{2} θ_{2} < 1 \\ \cos^{2} θ_{2} (- \cos^{4} θ_{2} + 2 \cos^{2} θ_{2} - 1) < 0 \\ - {(1 - \cos^{2} θ_{2})}^{2} < 0 \\ - \sin^{4} θ_{2} < 0 \end{array}$

La trayectoria parabólica termina, cuando la distancia de la partícula al origen A es r, se cumple entonces que x²+y²=r²

Rotaciones

La partícula describe la circunferencia vertical de radio r completa una y otra vez, suponiendo que el diámetro del obstáculo es muy pequeño, en la práctica describe una espiral, véase la página titulada Movimiento de una partícula atada a una cuerda que se enrolla en un cilindro horizontal (I)

La partícula de masa m describirá una circunferencia vertical de radio r con centro en A, si la tensión T en el punto más alto θ=π, el mayor o igual a cero

La situación límite se produce cuando T=0, en el punto más alto, θ=π

$m g = m \frac{v^{2}}{r}$

Aplicamos el principio de conservación de la energía, para calcular la velocidad v

$\begin{array}{l} r g = 2 g (l - r - L \cos θ_{0}) \\ \cos θ_{0} = \frac{5}{2} \frac{l}{L} - \frac{3}{2} \end{array}$

La partícula describirá una circunferencia vertical de radio r alrededor de A si

$θ_{0} \geq \arccos (\frac{5}{2} \frac{l}{L} - \frac{3}{2})$

Fijamos la desviación inicial θ₀ del péndulo

Fijamos la desviación inicial del péndulo θ₀=π/2. Sujetamos la partícula y ponemos el pendulo de longitud L en horizontal y lo soltamos

Rotaciones

La partícula describe una circunferencia vertical si

$\frac{5}{2} \frac{l}{L} - \frac{3}{2} \geq 0, \frac{l}{L} \geq \frac{3}{5}$

Oscilaciones

No hay oscilaciones ya que la partícula no se detiene para θ<π/2. Aplicando el principio de conservación de la energía para θ₀=π/2

$\begin{array}{l} 0 = 2 g (l + r \cos θ) \\ θ_{1} = \arccos (- \frac{l}{L - l}) \end{array}$

El ángulo θ₁ no existe o es mayor que π/2

Tiro parabólico

Describe un tiro parabólico, para los otros casos, l/L<3/5. El tiro parabólico comienza en la psición angular θ₂ con velocidad v₂

$\begin{array}{l} \cos θ_{2} = - \frac{2}{3} \frac{l}{r} \\ v_{2}^{2} = - r g \cos θ_{2} = - r g (- \frac{2}{3} \frac{l}{r}) = \frac{2}{3} g l \end{array}$

El alcance horizontal del proyectil es x, cuando y=0

$\begin{array}{l} {\begin{cases} x = - r \sin θ_{2} - v_{2} \cos θ_{2} \cdot t \\ 0 = - r \cos θ_{2} + v_{2} \sin θ_{2} \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ t = \frac{v_{2} \sin θ_{2} + \sqrt{v_{2}^{2} \sin^{2} θ_{2} - 2 g r \cos θ_{2}}}{g} \end{array}$

Para que impacte en el obstáculo A, x=0

$\begin{array}{l} 0 = - r \sin θ_{2} - v_{2} \cos θ_{2} \cdot \frac{v_{2} \sin θ_{2} + \sqrt{v_{2}^{2} \sin^{2} θ_{2} - 2 g r \cos θ_{2}}}{g} \\ - r \sqrt{1 - \frac{4 l^{2}}{9 r^{2}}} + \sqrt{\frac{2 g l}{3}} \frac{2 l}{3 r} \frac{\sqrt{\frac{2 g l}{3}} \sqrt{1 - \frac{4 l^{2}}{9 r^{2}}} + \sqrt{\frac{2 g l}{3} (1 - \frac{4 l^{2}}{9 r^{2}}) - 2 g r \frac{2}{3} \frac{l}{r}}}{g} = 0 \\ - r \sqrt{1 - \frac{4 l^{2}}{9 r^{2}}} + \sqrt{\frac{2 l}{3}} \frac{2 l}{3 r} \sqrt{r} {\sqrt{\frac{2 l}{3 r}} \sqrt{1 - \frac{4 l^{2}}{9 r^{2}}} + \sqrt{\frac{2 l}{r} - \frac{8 l^{3}}{27 r^{3}}}} = 0 \end{array}$

Llamamos u=2l/(3r)

$\begin{array}{l} - \sqrt{1 - u^{2}} + u \sqrt{u} {\sqrt{u} \sqrt{1 - u^{2}} + \sqrt{3 u - u^{3}}} = 0 \\ - \sqrt{1 - u^{2}} + u^{2} {\sqrt{1 - u^{2}} + \sqrt{3 - u^{2}}} = 0 \end{array}$

Llamamos x=u².

$x {\sqrt{1 - x} + \sqrt{3 - x}} - \sqrt{1 - x} = 0$

Resolvemos la ecuación en x utilizando la función fzero de MATLAB

>> f=@(x) x*(sqrt(1-x)+sqrt(3-x))-sqrt(1-x);
>> x0=fzero(f,[0,1])
x0 =    0.3333
>> sqrt(x0)
ans =    0.5774

Alternativamente, aislando y eliminando las raíces cuadradas, llegamos a una ecuación cúbica

$\begin{array}{l} x {\sqrt{1 - x} + \sqrt{3 - x}} = \sqrt{1 - x} \\ x^{2} (4 - 2 x + 2 \sqrt{1 - x} \sqrt{3 - x}) = 1 - x \\ 2 x^{2} \sqrt{1 - x} \sqrt{3 - x} = 1 - x - 4 x^{2} + 2 x^{3} \\ 4 x^{2} (3 - 4 x + x^{2}) = {(1 - x - 4 x^{2} + 2 x^{3})}^{2} \\ 12 x^{3} - 7 x^{2} - 2 x + 1 = 0 \end{array}$

Confirmamos por sustitución que x=1/3, es una raíz de la ecuación cúbica. Asimismo, empleando la función solve de Math Symbolic de MATLAB

>> syms x;
>> solve(12*x^3-7*x^2-2*x+1)
ans =
             1/3
1/8 - 17^(1/2)/8
17^(1/2)/8 + 1/8

De las tres raíces, la segunda es negativa y la tercera, comprobamos por sustitución que no es raíz de la ecuación

$x {\sqrt{1 - x} + \sqrt{3 - x}} = \sqrt{1 - x}$

Solamente es válida la primera raíz, x=u²=1/3. Despejamos l/L

$\begin{array}{l} u = \frac{2 l}{3 r} = \frac{2 l}{3 (L - l)} = \frac{\sqrt{3}}{3} \\ \frac{l}{L} = \frac{\sqrt{3}}{2 + \sqrt{3}} \end{array}$

El tiro parabólico comienza en la posición angular θ₂ con velocidad v₂

$\begin{array}{l} \cos θ_{2} = - 0.4641, θ_{2} = 125.1 º \\ v_{2} = \sqrt{\frac{2}{3} g l} = 1.7413 m/s \end{array}$

Actividades

El programa interactivo resuelve la ecuación del movimiento en la dirección tangencial por procedimientos numéricos

$\frac{d^{2} θ}{d t^{2}} + \frac{g}{r} \sin θ = 0$

donde r=L para el péndulo y r=L-l para el péndulo interrumpido

Las condiciones iniciales son las siguientes

Para el péndulo de longitud L

El péndulo se desvía θ₀ y se suelta

$t = 0, θ = θ_{0}, \frac{d θ}{d t} = 0$

Tarda un tiempo P₁/4 en alcanzar la parte más baja de la trayectoria circular de radio L centrada en O. En este instante, el hilo choca con el obtáculo A y se interrumpe su trayectoria circular de radio L centrada en O

Para el péndulo de longitud L-l

El péndulo parte en el instante P₁/4 de la posición θ=0 con velocidad angular

$\begin{array}{l} \frac{1}{2} m v^{2} = m g (L - L \cos θ_{0}) \\ v = 2 \sqrt{g L} \sin (\frac{θ_{0}}{2}) \\ \frac{d θ}{d t} = \frac{v}{L - l} \end{array}$

donde P₁ es el periodo del péndulo de longitud L

A partir de ese instante P₁/4, pueden ocurrir los distintos casos que ya se han descrito

Oscilaciones

El péndulo de longitud L-l describe media oscilación de amplitud θ₁ empleando un tiempo P₂/2. Como la energía se conserva, la velocidad es v en la parte más baja de la trayectoria θ=0. La velocidad angular es dθ/dt=-v/L, esta es la velocidad inicial para el péndulo de longitud L, que describe un cuarto de oscilación durante un tiempo P₁/4 y así, sucesivamente, hasta que el usuario detiene la animación

Tiro parabólico

Cuando la tensión del hilo se anula, T=0, en la posición θ₂, la partícua de masa m describe una trayectoria parabólica, hasta que su distancia al centro A se hace igual a r=L-l. En este instante, la animación se detiene

Rotaciones

El péndulo de longitud L-l describe trayectorias circulares del mismo radio cuyo centro es el obstáculo A, hasta que el usuario detiene la animación

Se introduce

La posición l del obstáculo A por debajo del centro de oscilación O
La desviación inicial θ₀ del péndulo
Se ha fijado la longitud del péndulo en L= 1 m

Se pulsa el botón titulado Nuevo

Observamos las distintas etapas del movimiento del péndulo interrumpido

Ejemplos

Sea l=0.7 m

Oscilaciones

Desviamos el péndulo θ₀=40° menor que arccos(l/L)=45.6° y lo soltamos

El péndulo oscila, entre los ángulos θ₀=40° y θ₁

$θ_{1} = \arccos (\frac{L \cos θ_{0} - l}{L - l}) = 77.3 º$

Con un periodo

$P = 2 \sqrt{\frac{L}{g}} K (k_{1}) + 2 \sqrt{\frac{L - l}{g}} K (k_{2}), k_{1} = \sin \frac{θ_{0}}{2}, k_{2} = \sin \frac{θ_{1}}{2}$

Con un periodo P=(P₁+P₂)/2=1.65 s

th_0=40*pi/180;
L=1; %longitud del péndulo
l=0.7; %posición obstáculo
th_1=acos((L*cos(th_0)-l)/(L-l));
P=2*sqrt(L/9.8)*ellipke(sin(th_0/2)^2)+2*sqrt((L-l)/9.8)*
ellipke(sin(th_1/2)^2);
disp(P)

1.6546

Tiro parabólico

Desviamos el péndulo θ₀=60° mayor que arccos(l/L)=45.6° y menor que arccos(5l/(2L)-3/2)=75.5° y lo soltamos

El péndulo de longitud L-l=0.3 m describe un arco de circunferencia vertical cuyo centro es el obstáculo A, hasta la posición angular θ₂

$θ_{2} = \arccos (\frac{2}{3} \frac{L \cos θ_{0} - l}{L - l}) = 116.4 º$

En esta posición comienza la trayectoria parabólica de ángulo de tiro π-θ₂

Rotaciones

Desviamos el péndulo θ₀=80° mayor que arccos(5l/(2L)-3/2)=75.5° y lo soltamos

El péndulo describe circunferencias verticales de radio r=L-l centradadas en el obstáculo A. Supondremos que el obstáculo tiene un diámetro muy pequeño. En la práctica, al enrollarse el hilo en el obstáculo, la partícula describe una espiral

Fijamos la desviación inicial del péndulo θ₀=90°

Oscilaciones

El ángulo θ₁ no existe o es mayor que 90°. No hay oscilaciones para este ejemplo

Rotaciones

Si l/L>0.6 (3/5), hay rotaciones

Tiro parabólico

Si l/L≤0.6 (3/5), por ejemplo l=0.55 m, la tensión se anula para el ángulo

$θ_{2} = \arccos (- \frac{2}{3} \frac{l}{L - l}) = 144.6 º$

A partir de esta posición, la partícula describe una trayectoria parabólica, hasta que su distancia al centro sea r=L-l

Comprobamos que la partícula impacta en el obstáculo A cuando l=0.4641 m

Posición (m): Angulo:

Referencias

Physics Challenge for Teachers and Students. For want of a nail...Solution to the December 2022 Challenge, The Physics Teacher, Vol. 60, December 2022, pp. 797

Physics Challenge for Teachers and Students. The pin and the pendulum. Solution to November 2012 Challenge, The Physics Teacher, Vol. 50, 2012.

Francisco Jose Torcal-Milla. Oscillation period of the truncated simple pendulum. Phys. Educ. 58 (2023) 025014

Fijamos la posición del obstáculo A

Oscilaciones, la posición final es θ1<π/2

Tensión del hilo nula, tiro parabólico

Rotaciones

Fijamos la desviación inicial θ0 del péndulo

Rotaciones

Oscilaciones

Tiro parabólico

Actividades

Ejemplos

Referencias

Oscilaciones, la posición final es θ₁<π/2

Fijamos la desviación inicial θ₀ del péndulo