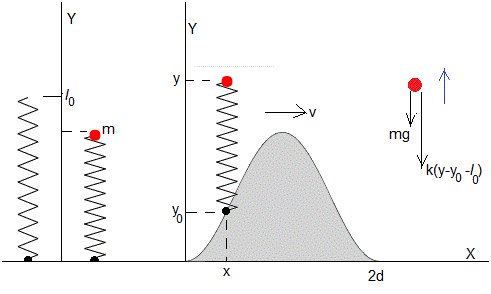
En la figura, observamos un muelle elástico de constante k en posición vertical. Su altura sin deformar es l₀. Cuando colocamos encima del muelle una partícula de masa m, su peso mg se equilibra con la fuerza que ejerce el muelle deformado kΔy. El muelle se deforma Δy=mg/k. La altura inicial de la partícula es l₀-mg/k, tal como vemos a la izquerda de la figura

Un automóvil viaja con velocidad horizontal constante v. Se encuentra con un obstáculo dispuesto a lo ancho de la calle cuya forma está descrita por la función

• y₀=A(1-cos(πx/d)) para 0<x<2d
• y₀=0 para x≥2d

tal como se aprecia en la parte derecha de la figura. Un muelle de constante elástica k describe el efecto sobre la suspensión del vehículo cuyo centro de masa (en color rojo) se representa por una partícula de masa m. Las ruedas pasan por encima del obstáculo y su centro, representado por un punto de color negro en el extremo inferior del muelle, describe una trayectoria de la misma forma que el obstáculo.

Vamos a considerar dos casos:

• Oscilaciones libres, no tenemos en cuenta el amortiguamiento de la suspensión del vehículo
• Oscilaciones amortiguadas, supondremos que dicho amortiguamiento se describe mediante una fuerza proporcional a la velocidad vertical dy/dt

Oscilaciones libres

En un instante t, la posición de la masa puntual es (x,y), con x=vt. Las fuerzas sobre la partícula (parte derecha de la figura) son:

• El peso, mg
• La fuerza que ejerce el muelle deformado y-y₀-l₀. y₀ es la posición de la parte inferior del muelle, l₀ es la longitud del muelle sin deformar

La ecuación del movimiento de la partícula en la dirección vertical es

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=-k\left(y-y_0-l_0\right)-mg\\ m\frac{d^{2}y}{d{t}^2}=-k\left(y-A-l_0+\frac{mg}{k}\right)-kA\cos \left(\frac{\pi vt}{d}\right)\end{array}}$

Llamando z=y-A-l₀+mg/k, ${\omega }_0^2=k/m$, ω_f=πv/d

${\displaystyle \frac{d^{2}z}{d{t}^2}+{\omega }_0^{2}z=-{\omega }_0^{2}A\cos \left({\omega }_{f}t\right)}$

La solución particular es y=Bcos(ω_ft).

${\displaystyle \begin{array}{l}-{\omega }_f^{2}B+{\omega }_0^{2}B=-{\omega }_0^{2}A\\ B=A\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\end{array}}$

La solución completa de la ecuación del movimiento es

${\displaystyle \begin{array}{l}z=C_1\cos \left({\omega }_{0}t\right)+C_2\sin \left({\omega }_{0}t\right)+A\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\cos \left({\omega }_{f}t\right)\\ y=C_1\cos \left({\omega }_{0}t\right)+C_2\sin \left({\omega }_{0}t\right)+A\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\cos \left({\omega }_{f}t\right)+A+l_0-\frac{g}{{\omega }_0^2}\end{array}}$

La velocidad vertical de la partícula es

${\displaystyle \frac{dy}{dt}=-{\omega }_0{C}_1\sin \left({\omega }_{0}t\right)+{\omega }_0{C}_2\cos \left({\omega }_{0}t\right)-A{\omega }_f\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\sin \left({\omega }_{f}t\right)}$

C₁ y C₂ se calculan a partir de las condiciones iniciales: en el instante t=0, y(0)=l₀-mg/k, dy/dt=0

${\displaystyle C_1=-A\frac{{\omega }_f^2}{{\omega }_f^2-{\omega }_0^2}{C}_2=0}$

La posición vertical y de la partícula en función del tiempo t es

${\displaystyle y=A-\frac{A}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2\cos \left({\omega }_{f}t\right)-{\omega }_f^2\cos \left({\omega }_{0}t\right)\right\}+l_0-\frac{g}{{\omega }_0^2}}$

La velocidad vertical de la partícula es

${\displaystyle \frac{dy}{dt}=A\frac{{\omega }_f{\omega }_0}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0\sin \left({\omega }_{f}t\right)-{\omega }_f\sin \left({\omega }_{0}t\right)\right\}}$

Movimiento final pasado el obstáculo

Cuando x≥2d, la posición del extremo inferior del muelle, y₀=0. La posición y velocidad de la partícula en el instante t₁=2d/v o cuando ω_ft₁=2π son:

${\displaystyle \begin{array}{l}{y}_1=A-\frac{A}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2-{\omega }_f^2\cos \left({\omega }_0{t}_1\right)\right\}+l_0-\frac{g}{{\omega }_0^2}\\ {\left(\frac{dy}{dt}\right)}_1=-A\frac{{\omega }_f^2{\omega }_0}{{\omega }_0^2-{\omega }_f^2}\cos \left({\omega }_0{t}_1\right)\end{array}}$

La ecuación del movimiento pasado el obstáculo, con y₀=0, es

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=-k\left(y-l_0\right)-mg\\ m\frac{d^{2}y}{d{t}^2}=-k\left(y-l_0+\frac{mg}{k}\right)\\ \frac{d^{2}z}{d{t}^2}+{\omega }_0^{2}z=0\end{array}}$

con z=y-l₀+mg/k

La solución de la ecuación diferencial que describe la oscilación libre es z=C₃cos(ω₀(t-t₁))+C₄sin(ω₀(t-t₁)), o bien

${\displaystyle \begin{array}{l}y=C_3\cos \left({\omega }_0(t-t_1)\right)+C_4\sin \left({\omega }_0(t-t_1)\right)+l_0-\frac{g}{{\omega }_0^2}\\ \frac{dy}{dt}=-{\omega }_0{C}_3\sin \left({\omega }_0(t-t_1)\right)+{\omega }_0{C}_4\cos \left({\omega }_0(t-t_1)\right)\end{array}}$

C₃ y C₄ se calculan a partir de las condiciones iniciales en el instante t₁, la altura de la partícula es y₁ y su velocidad es (dy/dt)₁

${\displaystyle C_4=\frac{1}{{\omega }_0}{\left(\frac{dy}{dt}\right)}_1{C}_3=y_1-l_0+\frac{g}{{\omega }_0^2}}$

Oscilaciones amortiguadas

Para describir el efecto del amortiguamiento, supondremos que además del peso y de la fuerza que ejerce el muelle, actúa sobre la partícula una fuerza proporcional a la velocidad vertical dy/dt y de sentido contrario a ésta. Añadimos a la ecuación diferencial el término 2γdz/dt como se ha descrito en las oscilaciones amortiguadas

${\displaystyle \frac{d^{2}z}{d{t}^2}+2\gamma \frac{dz}{dt}+{\omega }_0^{2}z=-{\omega }_0^{2}A\cos \left({\omega }_{f}t\right)}$

La posición vertical y de la partícula es

${\displaystyle \begin{array}{l}y=e^{-\gamma t}\left(C_1\cos \left(\omega t\right)+C_2\sin \left(\omega t\right)\right)+A\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\cos \left({\omega }_{f}t\right)+A+l_0-\frac{g}{{\omega }_0^2}\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\end{array}}$

ω es la frecuencia de las oscilaciones amortiguadas. La velocidad vertical de la partícula es

${\displaystyle \frac{dy}{dt}=e^{-\gamma t}\left\{\left(-\gamma C_1+\omega C_2\right)\cos \left(\omega t\right)-\left(\gamma C_2+\omega C_1\right)\sin \left(\omega t\right)\right\}-A{\omega }_f\frac{{\omega }_0^2}{{\omega }_f^2-{\omega }_0^2}\sin \left({\omega }_{f}t\right)}$

C₁ y C₂ se calculan a partir de las condiciones iniciales: en el instante t=0, y(0)=l₀-mg/k, dy/dt=0

${\displaystyle C_1=-A\frac{{\omega }_f^2}{{\omega }_f^2-{\omega }_0^2}{C}_2=\frac{\gamma }{\omega }{C}_1}$

La posición y de la partícula en función del tiempo t es

${\displaystyle y=A-\frac{A}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2\cos \left({\omega }_{f}t\right)-{\omega }_f^2{e}^{-\gamma t}\left(\cos \left(\omega t\right)+\frac{\gamma }{\omega }\sin \left(\omega t\right)\right)\right\}+l_0-\frac{g}{{\omega }_0^2}}$

La velocidad vertical de la partícula es

${\displaystyle \frac{dy}{dt}=A\frac{{\omega }_f}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2\sin \left({\omega }_{f}t\right)-{\omega }_f{e}^{-\gamma t}\left(\frac{{\gamma }^2}{\omega }+\omega \right)\sin \left(\omega t\right)\right\}}$

Movimiento final pasado el obstáculo

Cuando x≥2d, la posición del extremo inferior del muelle, y₀=0. La posición y velocidad de la partícula en el instante t₁=2d/v o cuando ω_ft₁=2π son:

${\displaystyle \begin{array}{l}{y}_1=A-\frac{A}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2\cos \left({\omega }_f{t}_1\right)-{\omega }_f^2{e}^{-\gamma t_1}\left(\cos \left(\omega t_1\right)+\frac{\gamma }{\omega }\sin \left(\omega t_1\right)\right)\right\}+l_0-\frac{g}{{\omega }_0^2}\\ {\left(\frac{dy}{dt}\right)}_1=A\frac{{\omega }_f}{{\omega }_0^2-{\omega }_f^2}\left\{{\omega }_0^2\sin \left({\omega }_f{t}_1\right)-{\omega }_f{e}^{-\gamma t_1}\left(\frac{{\gamma }^2}{\omega }+\omega \right)\sin \left(\omega t_1\right)\right\}\end{array}}$

La ecuación del movimiento pasado el obstáculo, con y₀=0, es

${\displaystyle \frac{d^{2}z}{d{t}^2}+2\gamma \frac{dz}{dt}+{\omega }_0^{2}z=0}$

con z=y-l₀+mg/k

La solución de la ecuación diferencial que describe la oscilación amortiguada es z=exp(t-t₁)·(C₃cos(ω₀(t-t₁))+C₄sin(ω₀(t-t₁))), o bien

${\displaystyle \begin{array}{l}y=e^{-\gamma (t-t_1)}\left\{C_3\cos \left(\omega (t-t_1)\right)+C_4\sin \left(\omega (t-t_1)\right)\right\}+l_0-\frac{g}{{\omega }_0^2}\\ \frac{dy}{dt}=e^{-\gamma (t-t_1)}\left\{\left(-\gamma C_3+\omega C_4\right)\cos \left(\omega (t-t_1)\right)-\left(\gamma C_4+\omega C_3\right)\sin \left(\omega (t-t_1)\right)\right\}\end{array}}$

C₁ y C₂ se calculan a partir de las condiciones iniciales: en el instante t=0, y(0)=l₀-mg/k, dy/dt=0

${\displaystyle C_4=\frac{1}{\omega }\left\{{\left(\frac{dy}{dt}\right)}_1+\gamma C_3\right\}{C}_3=y_1-l_0+\frac{g}{{\omega }_0^2}}$

Actividades

Se introduce

• La anchura 2d del obstáculo en el control titulado Anchura
• La altura A del obstáculo, en el control titulado Altura
• La velocidad v horizontal constante del vehículo en el control titulado Velocidad
• La constante de amortiguamiento γ en el control titulado Amortiguamiento

• Se ha fijado la frecuencia angular natural ${\omega }_0=\sqrt{g}$, ω₀= 3.13 rad/s. La frecuencia ω_f=πv/d, se puede modificar, cambiando la velocidad horizontal constante v o la anchura 2d del obstáculo

• Se ha fijado la altura inicial de la partícula antes de pasar el obstáculo $l_0-\frac{g}{{\omega }_0^2}=2.5$

Se pulsa el botón titulado Nuevo

Observamos el el efecto del obstáculo sobre el movimiento de la partícula (de color rojo). Se recomienda al lector estudiar los casos en los que la anchura del obstáculo es pequeña y la altura grande, para distintas velocidades del vehículo

En la parte superior derecha, se proporcionan los datos de:

• El tiempo t que trascurre desde el origen
• La posición horizontal x de la partícula
• La posición vertical y de la partícula
• La velocidad vertical dy/dt de la partícula
• La frecuencia ω_f=πv/d que se puede comparar con la frecuencia natural ω₀=3.13 rad/s fijada en el programa

Cuando el muelle se deforma de modo que la altura de la partícula y es inferior a la altura y₀, el programa se interrumpe, invitando al lector a cambiar los parámetros de entrada

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1083, pp. 131-132