En esta página, el modelo de calle irregular viene descrita por la función y₀=Asin(2πx/λ)

En la figura, observamos un muelle elástico de constante k en posición vertical. Su altura sin deformar es l₀. Cuando colocamos encima del muelle una partícula de masa m, su peso mg se equilibra con la fuerza que ejerce el muelle deformado kΔy. El muelle se deforma Δy=mg/k. La altura inicial de la partícula es l₀-mg/k, tal como vemos a la izquerda de la figura

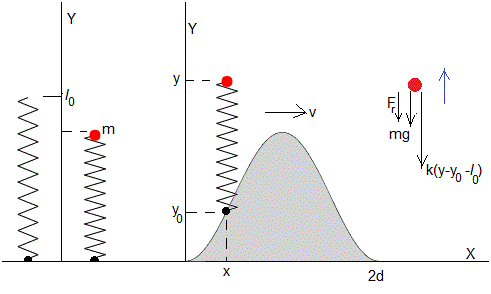
Un automóvil viaja con velocidad horizontal constante v. Se encuentra con un obstáculo dispuesto a lo ancho de la calle cuya forma está descrita por una función f(x) .

En un instante t, la posición de la masa puntual es (x,y), con x=vt. Las fuerzas sobre la partícula (parte derecha de la figura) son:

• El peso, mg

• La fuerza que ejerce el muelle deformado y-y₀-l₀.

y₀=f(x) es la posición de la parte inferior del muelle

• Supondremos que actúa una fuerza de rozamiento proporcional a la velocidad relativa

${\displaystyle F_r=-2\gamma m\frac{d(y-y_0)}{dt}}$

La ecuación del movimiento de la partícula en la dirección vertical es

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=-k\left(y-y_0-l_0\right)-mg-2\gamma m\frac{d(y-y_0)}{dt}\\ \frac{d^{2}y}{d{t}^2}+2\gamma \frac{dy}{dt}=-\frac{k}{m}\left(y-l_0+\frac{mg}{k}\right)+\frac{k}{m}{y}_0+2\gamma \frac{d{y}_0}{dt}\end{array}}$

Llamando

${\displaystyle {\omega }_0^2=\frac{k}{m},z=y-l_0+\frac{mg}{k}}$

La ecuación diferencial se expresa

${\displaystyle \frac{d^{2}z}{d{t}^2}+2\gamma \frac{dz}{dt}+{\omega }_0^{2}z={\omega }_0^{2}A\sin \left(\frac{2\pi vt}{\lambda }\right)+\frac{4\pi v}{\lambda }\gamma A\cos \left(\frac{2\pi vt}{\lambda }\right)}$

El segundo miembro es la fuerza oscilante por unidad de masa

${\displaystyle f(t)={\omega }_0^{2}A\sin \left({\omega }_{f}t\right)+2A\gamma {\omega }_f\cos \left({\omega }_{f}t\right),{\omega }_f=\frac{2\pi v}{\lambda }}$

La solución de la homogénea para γ<ω₀ (oscilaciones amortiguadas) es,

${\displaystyle z_h=\exp \left(-\gamma t\right)\left\{B_1\sin \left(\omega t\right)+B_2\cos \left(\omega t\right)\right\},\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

Los coeficientes B₁ y B₂ se determinan a partir de las condiciones iniciales

La solución particular es

${\displaystyle z_p=C\sin \left({\omega }_{f}t\right)+D\cos \left({\omega }_{f}t\right)}$

Introducimos la solución particular en la ecuación diferencial, para obtener los coeficientes C y D

${\displaystyle \begin{array}{l}-{\omega }_f^2\left(C\sin \left({\omega }_{f}t\right)+D\cos \left({\omega }_{f}t\right)\right)+2\gamma {\omega }_f\left(C\cos \left({\omega }_{f}t\right)-D\sin \left({\omega }_{f}t\right)\right)+{\omega }_0^2\left(C\sin \left({\omega }_{f}t\right)+D\cos \left({\omega }_{f}t\right)\right)\\ ={\omega }_0^{2}A\sin \left({\omega }_{f}t\right)+2\gamma {\omega }_{f}A\cos \left({\omega }_{f}t\right)\\ \{\begin{array}{l}-{\omega }_f^{2}C-2\gamma {\omega }_{f}D+{\omega }_0^{2}C={\omega }_0^{2}A\\ -{\omega }_f^{2}D+2\gamma {\omega }_{f}C+{\omega }_0^{2}D=2\gamma {\omega }_{f}A\end{array}\\ C=\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A,D=-\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\end{array}}$

La solución completa z=z_h+z_p es

${\displaystyle z=\exp \left(-\gamma t\right)\left\{B_1\sin \left(\omega t\right)+B_2\cos \left(\omega t\right)\right\}+\frac{\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}\sin \left({\omega }_{f}t\right)-2\gamma {\omega }_f^3\cos \left({\omega }_{f}t\right)}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A}$

La derivada dz/dt respecto del tiempo es

${\displaystyle \frac{dz}{dt}=-\gamma \exp \left(-\gamma t\right)\left\{B_1\sin \left(\omega t\right)+B_2\cos \left(\omega t\right)\right\}+\exp \left(-\gamma t\right)\omega \left\{B_1\cos \left(\omega t\right)-B_2\sin \left(\omega t\right)\right\}+\frac{\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}\cos \left({\omega }_{f}t\right)+2\gamma {\omega }_f^3\sin \left({\omega }_{f}t\right)}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{\omega }_{f}A}$

Las condiciones iniciales son

${\displaystyle t=0\{\begin{array}{l}z=0\\ \frac{dz}{dt}=0\end{array}}$

El móvil parte del origen en reposo. Los coeficientes B₁ y B₂ son

${\displaystyle \begin{array}{l}0=B_2-\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\\ 0=-\gamma B_2+\omega B_1+\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A{\omega }_f\\ \{\begin{array}{l}{B}_2=\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\\ B_1=-\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+2{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\frac{{\omega }_f}{\omega }A\end{array}\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}z=A\exp \left(-\gamma t\right)\left\{-\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+2{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\frac{{\omega }_f}{\omega }\sin \left(\omega t\right)+\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\cos \left(\omega t\right)\right\}+\frac{\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}\sin \left({\omega }_{f}t\right)-2\gamma {\omega }_f^3\cos \left({\omega }_{f}t\right)}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\\ z=\frac{A}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\left\{2\gamma {\omega }_f^3\left[\exp \left(-\gamma t\right)\cos \left(\omega t\right)-\cos \left({\omega }_{f}t\right)\right]+\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}\sin \left({\omega }_{f}t\right)-\frac{{\omega }_f}{\omega }\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+2{\gamma }^2{\omega }_f^2\right\}\exp \left(-\gamma t\right)\sin \left(\omega t\right)\right\}\end{array}}$

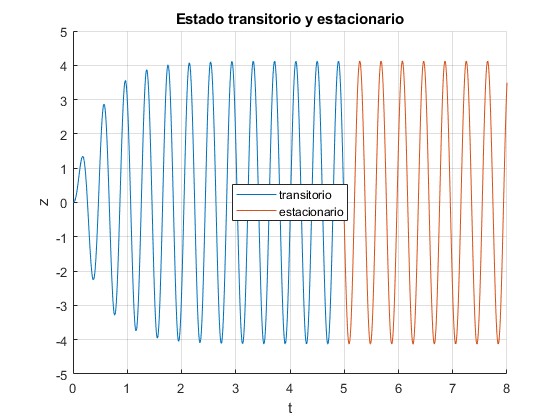
El estado estacionario

En el estado estacionario, t→∞, se termina el estado transsitorio descrito por la solución homogénea y se establece la solución particular de la ecuación diferencial

${\displaystyle z_{\infty }=\frac{\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}\sin \left({\omega }_{f}t\right)-2\gamma {\omega }_f^3\cos \left({\omega }_{f}t\right)}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A}$

Representamos z(t) con los siguientes datos

• Frecuencia propia ω₀=16
• Frecuencia de la fuerza oscilante ω_f=16
• Constante de amortiguamiento γ=2

g=2; %gamma
w0=16; %frecuencia propia
wf=16; %frecuencia de la fuerza oscilante
w=sqrt(w0^2-g^2);
zs=@(t) (((w0^2-wf^2)*w0^2+4*g^2*wf^2)*sin(wf*t)-2*g*wf^3*cos(wf*t))
/((w0^2-wf^2)^2+4*g^2*wf^2);
z=@(t) (2*g*wf^3*(exp(-g*t).*cos(w*t)-cos(wf*t))+
((w0^2-wf^2)*w0^2+4*g^2*wf^2)*sin(wf*t)-wf*((w0^2-wf^2)*w0^2
+2*g^2*wf^2)*exp(-g*t).*sin(w*t)/w)/((w0^2-wf^2)^2+4*g^2*wf^2);
hold on
fplot(z,[0,8])
fplot(zs,[5,8])
hold off
grid on
legend('transitorio','estacionario','Location','best')
xlabel('t')
ylabel('z')
title('Estado transitorio y estacionario')

Expresamos la solución particular de la ecuación diferencial que describe el oscilador forzado, de la forma equivalente

${\displaystyle \begin{array}{l}x=A_0\sin ({\omega }_{f}t-\delta )\hfill \\ x=A_0\cos \delta \sin ({\omega }_{f}t)-A_0\sin \delta \cos ({\omega }_{f}t)\hfill \end{array}}$

Calculamos la amplitud A₀ y la fase δ

${\displaystyle \begin{array}{l}{A}_0\cos \delta =\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\\ A_0\sin \delta =\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\\ A_0^2=\frac{{\left\{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2\right\}}^2+4{\gamma }^2{\omega }_f^6}{{\left\{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right\}}^2}{A}^2=\frac{{\omega }_0^4+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{A}^2\\ \tan \delta =\frac{2\gamma {\omega }_f^3}{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}\end{array}}$

Representamos la amplitud A₀ en función de la frecuencia ω_f de la fuerza oscilante.

• Frecuencia propia ω₀=16
• Constante de amortiguamiento γ=1

g=1; %gamma
w0=16; %frecuencia propia
A0=@(wf) sqrt(w0^4+4*g^2*wf.^2)./sqrt((w0^2-wf.^2).^2+4*g^2*wf.^2);
fplot(A0,[0,20])
grid on
xlabel('\omega_f')
ylabel('A_0')
title('Amplitud')

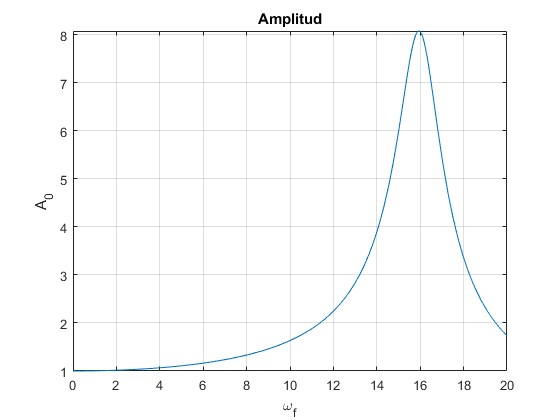
La amplitud tiene un valor máximo próximo a ω₀ si γ es pequeño.

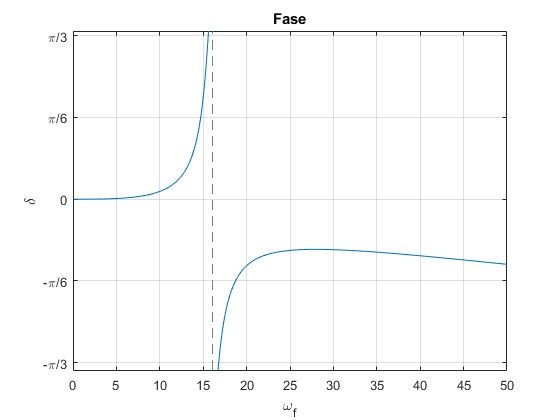
Representamos la fase δ en función de la frecuencia ω_f de la fuerza oscilante.

g=1; %gamma
w0=16; %frecuencia propia
delta=@(wf) atan((2*g*wf.^3)./((w0^2-wf.^2)*w0^2+4*g^2*wf.^2));
fplot(delta,[0,50])
set(gca,'YTick',-pi/2:pi/6:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/3', '-\pi/6','0','\pi/6','\pi/3','pi/2'})
grid on
xlabel('\omega_f')
ylabel('\delta')
title('Fase')

Energías

La energía almacenada en el muelle elástico

${\displaystyle E_1=\frac{1}{2}k{z}_{\infty }^2=\frac{1}{2}k{\left(A_1\sin \left({\omega }_{f}t\right)+A_2\cos \left({\omega }_{f}t\right)\right)}^2}$

Teniendo en cuenta los valores medios de una función periódica. <sin²(ω_ft)>=1/2, <cos²(ω_ft)>=1/2, <sin(ω_ft)cos(ω_ft)>=0

${\displaystyle \begin{array}{l}<E_1>=\frac{1}{2}k\left\{A_1^2<{\sin }^2\left({\omega }_{f}t\right)>+A_2^2<{\cos }^2\left({\omega }_{f}t\right)>+2A_1{A}_2<\cos \left({\omega }_{f}t\right)\sin \left({\omega }_{f}t\right)>\right\}\\ <E_1>=\frac{1}{4}k\left(A_1^2+A_2^2\right)=\frac{1}{4}k{A}_0^2\end{array}}$

• Energía por unidad de tiempo (potencia) disipada por la fuerza de rozamiento (por unidad de masa)

${\displaystyle \begin{array}{l}{P}_1=2\gamma \frac{dz}{dt}·\frac{dz}{dt}=2\gamma {\left(\frac{dz}{dt}\right)}^2=2\gamma {\omega }_f^2{\left(A_1\cos \left({\omega }_{f}t\right)-A_2\sin \left({\omega }_{f}t\right)\right)}^2\\ <P_1>=\gamma {\omega }_f^2\left(A_1^2+A_2^2\right)=\gamma {\omega }_f^2{A}_0^2\end{array}}$

• Energía por unidad de tiempo (potencia) suministrada por la fuerza oscilante (por unidad de masa)

${\displaystyle \begin{array}{l}{P}_2=f(t)·\frac{dz}{dt}=A\left({\omega }_0^2\sin \left({\omega }_{f}t\right)+2\gamma {\omega }_f\cos \left({\omega }_{f}t\right)\right){\omega }_f\left(A_1\cos \left({\omega }_{f}t\right)-A_2\sin \left({\omega }_{f}t\right)\right)=\\ A{\omega }_f\left\{\left({\omega }_0^2{A}_1-2\gamma {\omega }_f{A}_2\right)\sin \left({\omega }_{f}t\right)\cos \left({\omega }_{f}t\right)-{\omega }_0^2{A}_2{\sin }^2\left({\omega }_{f}t\right)+2\gamma {\omega }_f{A}_1{\cos }^2\left({\omega }_{f}t\right)\right\}\\ <P_2>=A{\omega }_f\left(\gamma {\omega }_f{A}_1-\frac{1}{2}{\omega }_0^2{A}_2\right)\\ <P_2>=A{\omega }_f\left(\gamma {\omega }_f\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A+\frac{1}{2}{\omega }_0^2\frac{2\gamma {\omega }_f^3}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}A\right)=\\ A^2{\omega }_f^2\gamma \left(\frac{\left({\omega }_0^2-{\omega }_f^2\right){\omega }_0^2+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}+\frac{{\omega }_0^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\right)=A^2{\omega }_f^2\gamma \frac{{\omega }_0^4+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}={\omega }_f^2\gamma A_0^2\end{array}}$

Comprobamos que en el estado estacionario, <P₁>=<P₂>

${\displaystyle <P>=A^2{\omega }_f^2\gamma \frac{{\omega }_0^4+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}}$

Calculamos el máximo de <P> utilizando Math Symbolic de MATLAB

>> syms x g w0;
>> y=x^2*(w0^4+4*g^2*x^2)/((w0^2-x^2)^2+4*g^2*x^2);
>> dy=diff(y,x);
>> solve(dy,x)

ans =    0
-((w0^5*(8*g^2 + w0^2)^(1/2) + 4*g^2*w0^4)/(- 16*g^4 + 8*g^2*w0^2 + w0^4))^(1/2)
-(-(w0^5*(8*g^2 + w0^2)^(1/2) - 4*g^2*w0^4)/(- 16*g^4 + 8*g^2*w0^2 + w0^4))^(1/2)
  ((w0^5*(8*g^2 + w0^2)^(1/2) + 4*g^2*w0^4)/(- 16*g^4 + 8*g^2*w0^2 + w0^4))^(1/2)
 (-(w0^5*(8*g^2 + w0^2)^(1/2) - 4*g^2*w0^4)/(- 16*g^4 + 8*g^2*w0^2 + w0^4))^(1/2)

La raíz válida es

${\displaystyle {\omega }_m=\sqrt{\frac{{\omega }_0^5\sqrt{8{\gamma }^2+{\omega }_0^2}+4{\gamma }^2{\omega }_0^4}{-16{\gamma }^4+8{\gamma }^2{\omega }_0^2+{\omega }_0^4}}}$

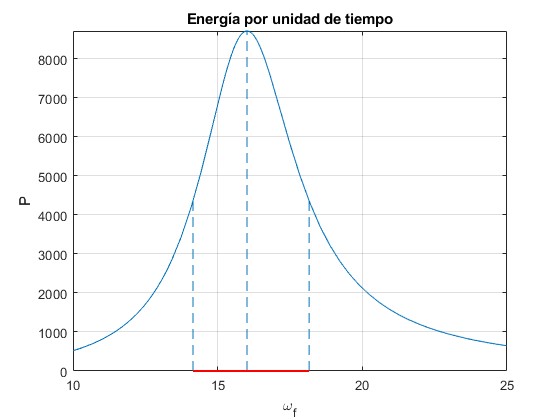
Representamos la energía por unidad de tiempo <P> en función de la frecuencia ω_f de la fuerza oscilante para

• Frecuencia propia ω₀=16
• Constante de amortiguamiento γ=2

Calculamos el intervalo de frecuencias para las cuales la potencia es superior a la mitad de la máxima <P_m>. Las dos raíces positivas de la ecuación bicuadrada

${\displaystyle \begin{array}{l}\frac{<P_m>}{2}=A^2{\omega }_f^2\gamma \frac{{\omega }_0^4+4{\gamma }^2{\omega }_f^2}{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}\\ \left(\frac{<P_m>}{2}-4{\gamma }^3\right){\omega }_f^4-\left({\omega }_0^4\gamma +<P_m>\left({\omega }_0^2-2{\gamma }^2\right)\right){\omega }_f^2+\frac{<P_m>}{2}{\omega }_0^4=0\end{array}}$

g=2; %gamma
w0=16; %frecuencia propia
P=@(wf) (g*wf.^2).*(w0^4+4*g^2*wf.^2)./((w0^2-wf.^2).^2+4*g^2*wf.^2);
wf_m=sqrt((w0^5*sqrt(8*g^2+w0^2)+4*g^2*w0^4)/(-16*g^4+8*g^2*w0^2+w0^4));
P_m=P(wf_m); %máximo
fplot(P,[10,25])
line([wf_m,wf_m],[0,P_m],'lineStyle','--')
a=P_m/(2*g)-4*g^2;
b=-(w0^4+P_m*(w0^2-2*g^2)/g);
c=P_m*w0^4/(2*g);
r1=(-b+sqrt(b^2-4*a*c))/(2*a);
r2=(-b-sqrt(b^2-4*a*c))/(2*a);
line([sqrt(r1),sqrt(r1)],[0,P_m/2],'lineStyle','--')
line([sqrt(r2),sqrt(r2)],[0,P_m/2],'lineStyle','--')
line([sqrt(r1),sqrt(r2)],[0,0],'lineWidth',1.5,'color','r')
grid on
xlabel('\omega_f')
ylabel('P')
title('Energía por unidad de tiempo')

Referencias

Kirk T. McDonald. Accelerating Through a Resonance on a “Washboard” Road. December, 2009