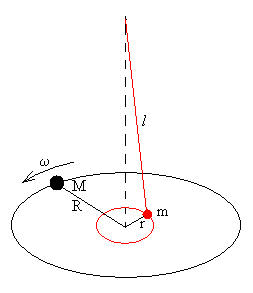
Una partícula de masa M describe un movimiento circular de radio R con velocidad angular constante ω. Un péndulo está hecho con un largo hilo inextensible de longitud l del que cuelga una partícula de masa m, está inicialmente en su posición de equilibrio. La fuerza de atracción entre las dos partículas hace que la partícula de masa m se mueva describiendo una trayectoria en forma de espiral cuando se cumple una determinada condición.

Las fuerzas que actúan sobre la partícula de masa m son:

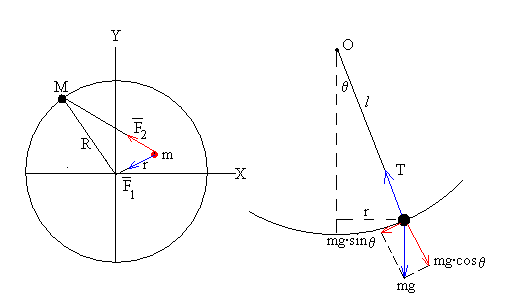
• La fuerza F₁ restauradora, que se produce cuando el péndulo está desviado un pequeño ángulo θ con respecto de la posición de equilibrio.

La componente tangencial del peso vale mg·sinθ, tal como se indica en la parte derecha de la figura. Si el ángulo θ es pequeño, podemos escribir

F₁≈ mg·sinθ=mgr/l

Las componentes de esta fuerza son (véase la figura más abajo)

${\displaystyle \begin{array}{l}{F}_{1x}=-F_1\frac{x}{r}=-mg\frac{x}{l}\\ F_{1y}=-F_1\frac{y}{r}=-mg\frac{y}{l}\end{array}}$



• La fuerza F₂ de atracción entre la partícula de masa m y la partícula de masa M, tiene por módulo

${\displaystyle F_2=G\frac{Mm}{{(R\cos \omega t-x)}^2+{(R\text{sin}\omega t-y)}^2}}$

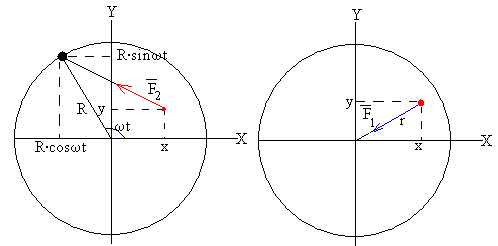
Las componentes de esta fuerza son

${\displaystyle \begin{array}{l}{F}_{2x}=G\frac{Mm(R\cos \omega t-x)}{{\left({(R\cos \omega t-x)}^2+{(R\text{sin}\omega t-y)}^2\right)}^{3/2}}\\ F_{2y}=G\frac{Mm(R\sin \omega t-y)}{{\left({(R\cos \omega t-x)}^2+{(R\text{sin}\omega t-y)}^2\right)}^{3/2}}\end{array}}$

La ecuación del movimiento de la partícula de masa m es

ma_x=F_1x+F_2x
ma_y=F_1y+F_2y

Si consideramos que el desplazamiento r del péndulo respecto de la posición de equilibrio es pequeño frente al radio R de la partícula de masa M, las componentes F_2x y F_2y se expresarán

${\displaystyle \begin{array}{l}{F}_{2x}\approx G\frac{Mm(R\cos \omega t-x)}{R^3}\\ F_{2y}\approx G\frac{Mm(R\sin \omega t-y)}{R^3}\end{array}}$

Las ecuaciones del movimiento se escriben en forma de ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+\left(\frac{g}{l}+\frac{GM}{R^3}\right)x=\frac{GM}{R^2}\cos \omega t\\ \frac{d^{2}y}{d{t}^2}+\left(\frac{g}{l}+\frac{GM}{R^3}\right)y=\frac{GM}{R^2}\text{sin}\omega t\end{array}}$

o bien

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+{\omega }_0^{2}x=\frac{GM}{R^2}\cos \omega t\\ \frac{d^{2}y}{d{t}^2}+{\omega }_0^{2}y=\frac{GM}{R^2}\text{sin}\omega t\end{array}}$

Se resuelve el sistema de dos ecuaciones diferenciales de segundo orden con las condiciones iniciales t=0, x=0, y=0, dx/dt=0, dy/dt=0, es decir, la partícula de masa m parte del origen con velocidad nula.

• Solución de la primera ecuación diferencial

La solución particular de la primera ecuación diferencial es x₁=K·cosωt

Introduciendo esta solución en la ecuación diferencial determinamos el valor de la constante K.

${\displaystyle x_1=\frac{GM}{R^2({\omega }_0^2-{\omega }^2)}\cos \omega t}$

La solución completa de la ecuación diferencial es

x=x₁+A·sinω₀t+B·cosω₀t

Las condiciones iniciales t=0, x=0, dx/dt=0 determinan los valores de las constantes A y B.

${\displaystyle x=\frac{GM}{R^2({\omega }_0^2-{\omega }^2)}\left(\cos (\omega t)-\cos ({\omega }_{0}t)\right)}$

• Solución de la segunda ecuación diferencial

La solución particular de la segunda ecuación diferencial es y₁=K·sinωt

Introduciendo esta solución en la ecuación diferencial determinamos el valor de la constante K.

${\displaystyle y_1=\frac{GM}{R^2({\omega }_0^2-{\omega }^2)}\text{sin}\omega t}$

La solución completa de la ecuación diferencial es

y=y₁+A·sinω₀t+ B·cosω₀t

Las condiciones iniciales t=0, y=0, dy/dt=0 determinan los valores de las constantes A y B.

${\displaystyle y=\frac{GM}{R^2({\omega }_0^2-{\omega }^2)}\left(\sin (\omega t)-\frac{\omega }{{\omega }_0}\sin ({\omega }_{0}t)\right)}$

Caso particular

Cuando ω≈ω₀ tenemos para la solución de la primera ecuación diferencial

${\displaystyle \underset{\omega \to {\omega }_0}{\lim }\frac{\cos \omega t-\cos {\omega }_{0}t}{{\omega }_0^2-{\omega }^2}=\underset{\omega \to {\omega }_0}{\lim }\frac{-2\text{sin}\left(\frac{\omega +{\omega }_0}{2}t\right)}{({\omega }_0+\omega )}·\frac{\text{sin}\left(\frac{\omega -{\omega }_0}{2}t\right)}{({\omega }_0-\omega )}=\frac{\sin \omega t}{\omega }·\frac{t}{2}}$

La solución de la primera ecuación diferencial se convierte en

${\displaystyle x=\frac{GM}{R^2}\frac{t}{2\omega }\sin \omega t}$

Para la solución de la segunda ecuación diferencial

${\displaystyle \underset{\omega \to {\omega }_0}{\lim }\frac{{\omega }_0\sin \omega t-\omega \sin {\omega }_{0}t}{{\omega }_0({\omega }_0^2-{\omega }^2)}=\underset{\omega \to {\omega }_0}{\lim }\frac{2\text{cos}\left(\frac{\omega +{\omega }_0}{2}t\right)}{({\omega }_0+\omega )}·\frac{\sin \left(\frac{\omega -{\omega }_0}{2}t\right)}{({\omega }_0-\omega )}=-\frac{\text{cos}\omega t}{\omega }·\frac{t}{2}}$

La solución de la segunda ecuación diferencial se convierte en

${\displaystyle y=-\frac{GM}{R^2}\frac{t}{2\omega }\text{cos}\omega t}$

La distancia r de la partícula de masa m al origen es

${\displaystyle r=\sqrt{x^2+y^2}=\frac{GM}{R^2}\frac{t}{2\omega }}$

La distancia r se incrementa proporcionalmente al tiempo t, la partícula describe una espiral que parte del origen.

Tenemos que diseñar nuestro experimento simulado de modo que la frecuencia

${\displaystyle {\omega }_0=\sqrt{\frac{g}{l}+\frac{GM}{R^3}}}$

coincida con gran aproximación con la velocidad angular ω de rotación de la partícula de masa M.

Ejemplo

• Sea la masa M=50 kg de la partícula que describe el movimiento circular de radio R=8 cm=0.08 m
• La longitud del péndulo es l=1.2 m
• La aceleración de la gravedad g=9.8 m/s²
• La constante de la gravitación universal es G=6.67·10^-11 Nm²/kg²

La frecuencia

${\displaystyle {\omega }_0=\sqrt{\frac{9.8}{1.2}+\frac{6.67·{10}^{-11}·50}{{0.08}^3}}=2.857739\text{rad/s}}$

se diferencia muy poco de la frecuencia angular de oscilación del péndulo, debido a que el segundo término que contiene la constante G es muy pequeño.

Supongamos que la velocidad angular de rotación ω=3 rad/s. Calculamos x e y en el instante t=1hora=3600 s

${\displaystyle x=\frac{6.67·{10}^{-11}50}{{0.08}^2({2.857739}^2-3^2)}\left(\cos 10800-\cos 10287.86\right)=-8.48·{10}^{-7}\text{m}}$

Lo mismo ocurre para y. El péndulo no se desvía apenas del origen, incluso después de un tiempo muy grande.

G=6.67e-11; %costante G
M=50; %masa que gira
R=0.08; %radio 
w=3; %velocidad angular de rotación
longitud=1.2; %péndulo

w0=sqrt(9.8/1.2+G*M/R^3);
x=@(t) G*M*(cos(w*t)-cos(w0*t))/(R^2*(w0^2-w^2));
y=@(t) G*M*(sin(w*t)-w*cos(w0*t)/w0)/(R^2*(w0^2-w^2));
r=@(t) sqrt(x(t).^2+y(t).^2);
disp(r(3600))

  8.4819e-07

La desviación se incrementa apreciablemente cuando ω≈ω₀=2.857739, al cabo de una hora la desviación del péndulo es

${\displaystyle r=\frac{GM}{R^2}\frac{t}{2\omega }=\frac{6.67·{10}^{-11}·50}{{0.08}^2}\frac{1·3600}{2·2.857739}=0.328·{10}^{-3}\text{m}=\text{0}\text{.328}\text{mm}}$

G=6.67e-11; %costante G
M=50; %masa que gira
R=0.08; %radio 
longitud=1.2; %péndulo

w0=sqrt(9.8/1.2+G*M/R^3);
r=@(t) G*M*t/(2*R^2*w0);
disp(r(3600))

   3.2822e-04

Comprobaremos que cuando ω≈ω₀ la desviación r

• Es proporcional a la masa M
• Es inversamente proporcional al cuadrado del radio R de la partícula de masa M que describe la trayectoria circular.
• Es proporcional al tiempo t.

Para cada valor del tiempo t, medimos el valor del radio r de la circunferencia que describe.

• en el eje vertical, se representa la desviación del péndulo r en mm,
• en el eje horizontal, el tiempo transcurrido t en horas.

t=0.5:0.5:5;
r=[0.164,0.328,0.492,0.657,0.821,0.985,1.149,1.313,1.477,1.641];
plot(t,r,'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('t(s)')
ylabel('r(mm)')
title('Medida de la constante G')

En el menú de la ventana gráfica, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

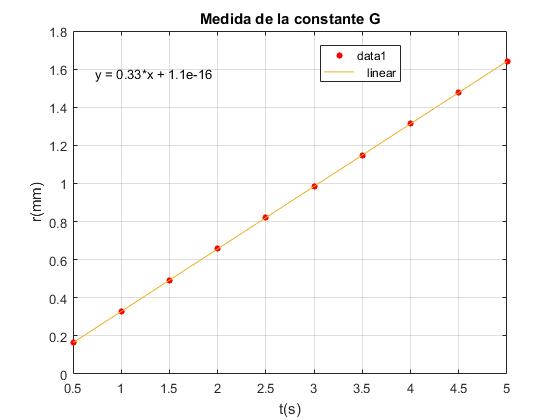
Como hemos deducido en el apartado anterior

${\displaystyle r=\frac{GM}{2R^2\omega }t}$

Se obtendrá el valor de G a partir de la medida de pendiente p1=0.32825 de la recta que mejor ajusta a los datos experimentales

${\displaystyle \frac{0.32825}{1000·3600}=\frac{G·50}{2·{0.08}^2·2.8577}G=6.665·{10}^{-11}\frac{\text{N}{\text{m}}^{\text{2}}}{{\text{kg}}^{\text{2}}}}$

Actividades

Se introduce

• La masa M de la partícula en kg, que describe el movimiento circular, en el control titulado Masa
• El radio R de la circunferencia que describe en cm, en el control titulado Radio, el valor introducido deberá estar comprendido entre 6 y 10 cm.
• La velocidad angular de rotación ω, en rad/s, en el control titulado V. angular
• La longitud del péndulo se ha fijado en el valor l=1.2 m

Se pulsa el botón titulado Nuevo y a continuación, de pulsa en el botón titulado ►.

Observamos el movimiento circular de la partícula de masa M, el péndulo estará prácticamente inmóvil en el origen. En la parte superior izquierda, se indica el instante t en segundos y la desviación del péndulo (distancia al origen) r en mm.

Introducimos el tiempo t, medido en horas, en el control titulado Tiempo y pulsamos el botón titulado Nuevo. Se observa el movimiento del péndulo en dicho instante y posteriores. Anotamos la distancia al origen r.

Volvemos a introducir otro tiempo medido en horas en el control titulado Tiempo y pulsamos el botón titulado Nuevo, anotamos la distancia r y así, sucesivamente. De este modo, cremos una tabla de datos 'experimentales' t (en horas), r (radio en mm). La pendiente de la recta que mejor ajusta permite deducir el valor de la constante G

Podemos cambiar la escala de observación, activando alguno de los botones de radio titulados dm, cm y mm. En la primera escala dm observamos el movimiento circular de la partícula de masa M, en las otras escalas está muy alejada del origen y desaparece de la ventana gráfica.

El péndulo no se desviará apenas de su posición de equilibrio si ω es distinto de ω₀, tal como podemos comprobar y calcular a partir de las ecuaciones del movimiento y observamos activando el botón de radio titulado mm.

Se debe procurar introducir un tiempo t que no sea lo suficientemente grande como para que deje de cumplirse la condición de que r<<R, en la que nos hemos basado para obtener una expresión simple que describa aproximadamente el movimiento del péndulo.

Referencias

Sheppard D. Using one pendulum and a rotating mass to measure the Universal Gravitational Constant. Am. J. Phys. 38 (1970), pp. 380