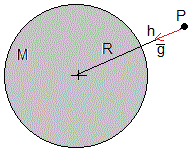
Sea una esfera homogénea de masa M y radio R, en reposo, la aceleración de la gravedad disminuye con la altura h.

${\displaystyle g=G\frac{M}{{\left(R+h\right)}^2}=G\frac{M}{R^2}{\left(1+\frac{h}{R}\right)}^{-2}\approx g_0\left(1-2\frac{h}{R}\right)}$

>> syms x;
>> taylor((1+x)^-2,x)
ans =- 6*x^5 + 5*x^4 - 4*x^3 + 3*x^2 - 2*x + 1 

Geometrías planas

Vamos a determinar el incremento de la aceleración de la gravedad en el pico de una montaña para geometrías simples, debido a la masa de la misma

Como en el campo eléctrico comenzaremos con el anillo y el disco que servirán de base para otras configuraciones, cilindro, tronco de cono, etc.

Anillo

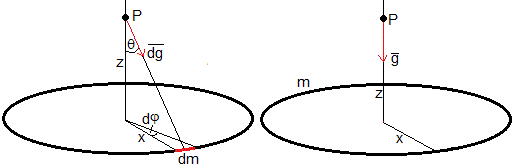
Calculamosla aceleración de la gravedad debida a un elemento diferencial de masa dm en un punto P del eje Z, situado a una altura z

${\displaystyle G\frac{dm}{x^2+z^2}=G\frac{\lambda \left(x·d\phi \right)}{x^2+z^2}=G\frac{m}{2\pi x}\frac{x·d\phi }{x^2+z^2}=G\frac{m}{2\pi }\frac{d\phi }{x^2+z^2}}$

λ es la densidad lineal de masa m/(2πx)

Las componentes horizontales de la aceleración de la gravedad producida por los distintos elementos dm se anulan por simetría, quedando solamente las componentes a lo largo del eje Z que se suman

${\displaystyle G\frac{m}{2\pi }\frac{d\phi }{x^2+z^2}\cos \theta =G\frac{m}{2\pi }\frac{d\phi }{x^2+z^2}\frac{z}{\sqrt{x^2+z^2}}=G\frac{m}{2\pi }\frac{z}{{\left(x^2+z^2\right)}^{3/2}}d\phi }$

Integramos respecto del ángulo φ entre 0 y 2π

${\displaystyle \begin{array}{l}g=G\frac{m}{2\pi }\frac{z}{{\left(x^2+z^2\right)}^{3/2}}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\phi }=Gm\frac{z}{{\left(x^2+z^2\right)}^{3/2}}\\ \overrightarrow{g}=-Gm\frac{z}{{\left(x^2+z^2\right)}^{3/2}}\widehat{k}\end{array}}$

Disco

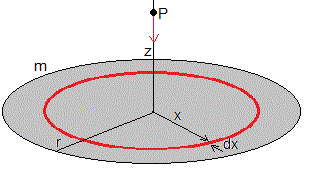
Sea un disco de masa m y radio r, calculamos la aceleración de la gravedad en un punto P del eje, distante z

Dividimos el disco en anillos de radio x y anchura dx, la masa contenida en cada anillo es dm=σ(2πx·dx). La aceleración de la gravedad de esta porción del disco es

${\displaystyle G\frac{z}{{\left(x^2+z^2\right)}^{3/2}}dm=G\frac{z}{{\left(x^2+z^2\right)}^{3/2}}\sigma \left(2\pi x·dx\right)=2G\frac{m}{r^2}z\frac{x}{{\left(x^2+z^2\right)}^{3/2}}dx}$

σ es la densidad del disco de σ=m/(πr²)

La aceleración de la gravedad debida al disco en el punto P es la suma de la producida por todos los anillos

${\displaystyle g=2G\frac{m}{r^2}z{\displaystyle \underset{0}{\overset{r}{\int }}\frac{x}{{\left(x^2+z^2\right)}^{3/2}}dx}=2G\frac{m}{r^2}z{\frac{1}{2}\frac{{\left(x^2+z^2\right)}^{-1/2}}{-\frac{1}{2}}|}_0^r=2G\frac{m}{r^2}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)}$

Cilindro

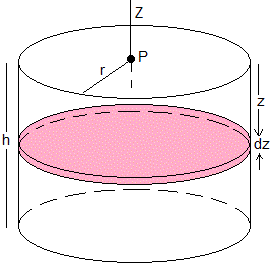
Vamos a calcular la aceleración de la gravedad en P producida por un cilindro de densidad ρ, radio r y altura h.

Dividimos el cilindro en discos de radio r y espesor dz. La aceleración de la gravedad en P debida al disco que dista z de su centro es

${\displaystyle \begin{array}{l}2G\frac{dm}{r^2}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)=2G\frac{\rho \pi r^2·dz}{r^2}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)\\ =2\pi G\rho \left(1-\frac{z}{\sqrt{r^2+z^2}}\right)dz\end{array}}$

La aceleración de la gravedad en P debida por todos los discos es

${\displaystyle \Delta g=2\pi G\rho {\displaystyle \underset{0}{\overset{h}{\int }}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)dz}=2\pi G\rho \left(h-\sqrt{r^2+h^2}+r\right)}$

Denominamos al parámetro k=r/h

${\displaystyle \Delta g=2\pi G\rho h\left(1-\sqrt{k^2+1}+k\right)}$

Tronco de cono

Sea un tronco de cono de altura h y radio de la base kh

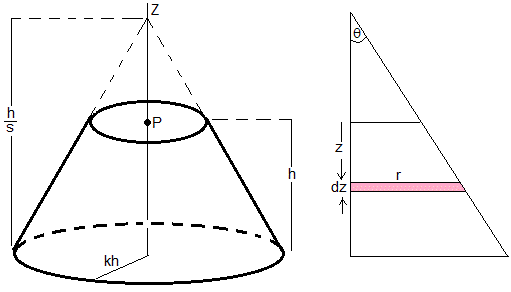
Dividimos el tronco de cono en discos de radio r y espesor dz, la aceleración de la gravedad debida a una de estos discos en el punto P distante z del centro del disco es

${\displaystyle 2G\frac{dm}{r^2}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)=2G\frac{\rho \pi r^2·dz}{r^2}\left(1-\frac{z}{\sqrt{r^2+z^2}}\right)=2\pi G\rho \left(1-\frac{z}{\sqrt{r^2+z^2}}\right)dz}$

Los discos no tienen el mismo radio, la relación entre r y z es

${\displaystyle \tan \theta =\frac{kh}{\frac{h}{s}}=\frac{r}{\frac{h}{s}-h+z},r=ks\left(z+\frac{h}{s}-h\right)=k\left(zs+\left(1-s\right)h\right)}$

La aceleración de la gravedad en P debida a todos los discos que forman el tronco de cono es

${\displaystyle \begin{array}{l}\Delta g=2\pi G\rho {\displaystyle \underset{0}{\overset{h}{\int }}\left(1-\frac{z}{\sqrt{k^2{\left(zs+\left(1-s\right)h\right)}^2+z^2}}\right)dz}=\\ 2\pi G\rho \left\{h-{\displaystyle \underset{0}{\overset{h}{\int }}\frac{z}{\sqrt{\left(1+k^2{s}^2\right)z^2+2s\left(1-s\right)k^{2}hz+{\left(1-s\right)}^2{k}^2{h}^2}}dz}\right\}\end{array}}$

Para resolver la integral, llamamos u al radicando

${\displaystyle \begin{array}{l}u=\left(1+k^2{s}^2\right)z^2+2s\left(1-s\right)k^{2}hz+{\left(1-s\right)}^2{k}^2{h}^2\\ du=\left(2\left(1+k^2{s}^2\right)z+2s\left(1-s\right)k^{2}h\right)dz\\ zdz=\frac{du-2s\left(1-s\right)k^{2}h·dz}{2\left(1+k^2{s}^2\right)}\end{array}}$

La integral se convierte en la suma de dos integrales

${\displaystyle \frac{1}{2\left(1+k^2{s}^2\right)}{\displaystyle \int \frac{du}{\sqrt{u}}-\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}{\displaystyle \int \frac{dz}{\sqrt{\left(1+k^2{s}^2\right)z^2+2s\left(1-s\right)k^{2}hz+{\left(1-s\right)}^2{k}^2{h}^2}}}}}$

La primera integral es inmediata, la segunda es del tipo

${\displaystyle \frac{1}{1+k^2{s}^2}\sqrt{k^2{\left(zs+\left(1-s\right)h\right)}^2+z^2}-\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}{\displaystyle \int \frac{dz}{\sqrt{a{z}^2+bz+c}},}\{\begin{array}{l}a=1+k^2{s}^2\\ b=2s\left(1-s\right)k^{2}h\\ c={\left(1-s\right)}^2{k}^2{h}^2\end{array}}$

Completamos cuadrados en el radicando

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dz}{\sqrt{a{z}^2+bz+c}}}={\displaystyle \int \frac{dz}{\sqrt{a\left\{\frac{c}{a}-\frac{b^2}{4a^2}+{\left(z+\frac{b}{2a}\right)}^2\right\}}}=}\frac{1}{\sqrt{a}}\ln \left(z+\frac{b}{2a}+\sqrt{\frac{c}{a}-\frac{b^2}{4a^2}+{\left(z+\frac{b}{2a}\right)}^2}\right)=\\ \frac{1}{\sqrt{a}}\ln \left(z+\frac{b}{2a}+\sqrt{z^2+\frac{b}{a}z+\frac{c}{a}}\right)=\frac{1}{\sqrt{1+k^2{s}^2}}\ln \left(z+\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}+\sqrt{z^2+\frac{2s\left(1-s\right)k^{2}h}{1+k^2{s}^2}z+\frac{{\left(1-s\right)}^2{k}^2{h}^2}{1+k^2{s}^2}}\right)\end{array}}$

Una vez que se han resuelto las integrales, la aceleración de la gravedad vale

${\displaystyle \begin{array}{l}\Delta g=2\pi G\rho \left\{h-{\frac{1}{1+k^2{s}^2}\sqrt{k^2{\left(zs+\left(1-s\right)h\right)}^2+z^2}+\frac{s\left(1-s\right)k^{2}h}{{\left(1+k^2{s}^2\right)}^{3/2}}\ln \left(z+\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}+\sqrt{z^2+\frac{2s\left(1-s\right)k^{2}h}{1+k^2{s}^2}z+\frac{{\left(1-s\right)}^2{k}^2{h}^2}{1+k^2{s}^2}}\right)|}_0^h\right\}=\\ 2\pi G\rho h\left\{1-\frac{\sqrt{k^2+1}-k\left(1-s\right)}{1+k^2{s}^2}+\frac{s\left(1-s\right)k^2}{{\left(1+k^2{s}^2\right)}^{3/2}}\ln \left(h+\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}+\frac{h\sqrt{1+k^2}}{\sqrt{1+k^2{s}^2}}\right)-\frac{s\left(1-s\right)k^{2}h}{{\left(1+k^2{s}^2\right)}^{3/2}}\ln \left(\frac{s\left(1-s\right)k^{2}h}{1+k^2{s}^2}+\frac{\left(1-s\right)kh}{\sqrt{1+k^2{s}^2}}\right)\right\}\end{array}}$

Agrupando términos

${\displaystyle \Delta g=2\pi G\rho h\left\{1-\frac{\sqrt{k^2+1}-k\left(1-s\right)}{1+k^2{s}^2}+\frac{s\left(1-s\right)k^2}{{\left(1+k^2{s}^2\right)}^{3/2}}\ln \left(\frac{1+k^2{s}^2+\sqrt{1+k^2}\sqrt{1+k^2{s}^2}}{k(1-s)\left(ks+\sqrt{1+k^2{s}^2}\right)}\right)\right\}}$

Cono

Cuando s=1, tenemos un cono

${\displaystyle \Delta g=2\pi G\rho h\left\{1-\frac{\sqrt{k^2+1}}{1+k^2}\right\}=2\pi G\rho h\left(1-\frac{1}{\sqrt{k^2+1}}\right)}$

Ejemplo

Representamos gráficamente

${\displaystyle \frac{\Delta g}{2\pi G\rho h}=f(k)}$

la función f(k) para un

• cilindro
• tronco de cono con s=1/2
• tronco de cono con s=3/2
• cono

f=@(k) 1-sqrt(k.^2+1)+k; %cilindro
hold on
fplot(f,[3,50])
s=1/2; %tronco de cono
f=@(k) 1-(sqrt(k.^2+1)-k*(1-s))./(1+k.^2*s^2)+(s*(1-s)*k.^2).*log((1+k.^2*s^2+
sqrt(1+k.^2).*sqrt(1+k.^2*s^2))./(k*(1-s).*(k*s+sqrt(1+k.^2*s^2)))).
/(1+k.^2*s^2).^(3/2);
fplot(f,[3,50])
s=2/3; %tronco de cono
f=@(k) 1-(sqrt(k.^2+1)-k*(1-s))./(1+k.^2*s^2)+(s*(1-s)*k.^2).*log((1+k.^2*s^2+
sqrt(1+k.^2).*sqrt(1+k.^2*s^2))./(k*(1-s).*(k*s+sqrt(1+k.^2*s^2)))).
/(1+k.^2*s^2).^(3/2);
fplot(f,[3,50])
f=@(k) 1-1./sqrt(k.^2+1); %cono
fplot(f,[3,50])
hold off
grid on
xlabel('k')
legend('cilindro','t. cono, 1/2','t. cono,2/3','cono','location','best')
ylabel('\Deltag')
title('Gravedad debida a una montaña')

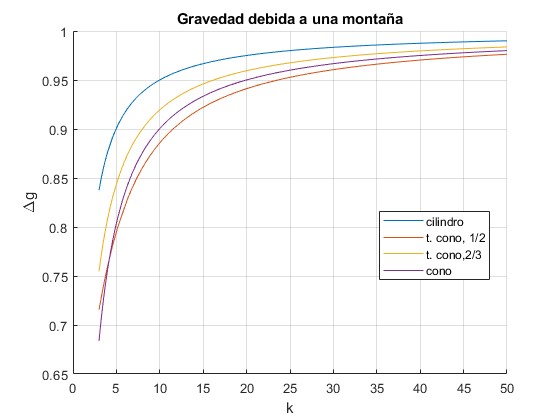
Nota: los resultados para el tronco de cono difieren de la tabla 1 del artículo citado en las referencias

Capa esférica

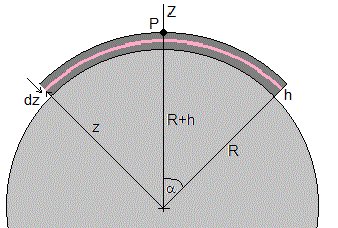
Las grandes planicies sobre la superficie de la Tierra miden cientos de km por lo que hay que tener en cuenta la esfericidad de la Tierra. Simulamos una planicie mediante una capa esférica de longitud 2αR y de altura h.

Primero, calculamos la aceleración de la gravedad debida a la capa esférica de longitud 2zα y de espesor dz comprendida entre z y z+dz

Dividimos esta capa esférica en anillos de radio x=zsinθ (en color rosa en la figura más abajo), la sección de cada anillo es dz(z·dθ) y la longitud del anillo es 2πx.

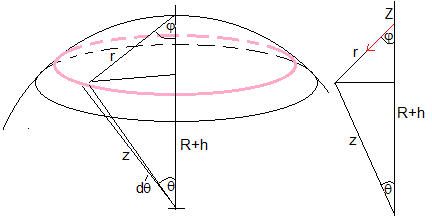
La masa del anillo es

${\displaystyle dm=\rho \left(2\pi z\sin \theta \right)\left(z·d\theta ·dz\right)=2\pi \rho z^2\sin \theta ·d\theta ·dz}$

La distancia r del anillo al punto P es

${\displaystyle r^2=u^2+z^2-2uz\cos \theta }$

Para abreviar la notación llamamos, u=R+h

La aceleración de la gravedad en el punto P es

${\displaystyle G\frac{dm}{r^2}}$

Las componentes horizontales se anulan por simetría, quedando solamente las componentes a lo largo del eje Z

${\displaystyle G\frac{dm}{r^2}\cos \phi =G\frac{dm}{r^2}\frac{u-z\cos \theta }{r}=2\pi \rho G\frac{z^2\sin \theta ·\left(u-z\cos \theta \right)}{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta ·dz}$

Integramos respecto de θ entre 0 y α

${\displaystyle 2\pi \rho G{z}^2\left({\displaystyle \underset{0}{\overset{\alpha }{\int }}\frac{\sin \theta ·\left(u-z\cos \theta \right)}{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta }\right)dz}$

La integral es la suma de dos integrales

${\displaystyle \frac{\sin \theta ·\left(u-z\cos \theta \right)}{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta =u{\displaystyle \int \frac{\sin \theta }{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta -z{\displaystyle \int \frac{\sin \theta ·\cos \theta }{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta }}}$

La primera integral es inmediata

${\displaystyle {\displaystyle \int \frac{\sin \theta }{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta }=\frac{1}{uz}\frac{-1}{\sqrt{u^2+z^2-2uz\cos \theta }}}$

La segunda integral se resuelve por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{\sin \theta ·\cos \theta }{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta },\{\begin{array}{l}U=\cos \theta ,dU=-\sin \theta ·d\theta \\ dV=\frac{\sin \theta }{{\left(u^2+z^2-2uz\cos \theta \right)}^{3/2}}d\theta ,V=\frac{1}{uz}\frac{-1}{\sqrt{u^2+z^2-2uz\cos \theta }}\end{array}\\ =\frac{1}{uz}\frac{-\cos \theta }{\sqrt{u^2+z^2-2uz\cos \theta }}-\frac{1}{uz}{\displaystyle \int \frac{\sin \theta ·d\theta }{\sqrt{u^2+z^2-2uz\cos \theta }}}=-\frac{1}{uz}\frac{\cos \theta }{\sqrt{u^2+z^2-2uz\cos \theta }}-\frac{1}{u^2{z}^2}\sqrt{u^2+z^2-2uz\cos \theta }\end{array}}$

Agrupamos términos y evaluamos entre los límites 0 y α

${\displaystyle \begin{array}{l}2\pi \rho G{z}^2\left({\frac{1}{z}\frac{-1}{\sqrt{u^2+z^2-2uz\cos \theta }}+\frac{1}{u}\frac{\cos \theta }{\sqrt{u^2+z^2-2uz\cos \theta }}+\frac{1}{u^{2}z}\sqrt{u^2+z^2-2uz\cos \theta }|}_0^{\alpha }\right)dz=\\ 2\pi \rho G{z}^2\left({\frac{-u+z\cos \theta }{uz\sqrt{u^2+z^2-2uz\cos \theta }}+\frac{1}{u^{2}z}\sqrt{u^2+z^2-2uz\cos \theta }|}_0^{\alpha }\right)dz=\\ \frac{2\pi \rho G{z}^2}{uz}\left({\frac{-u+z\cos \theta }{\sqrt{u^2+z^2-2uz\cos \theta }}+\frac{1}{u}\sqrt{u^2+z^2-2uz\cos \theta }|}_0^{\alpha }\right)dz=\\ \frac{2\pi \rho G{z}^2}{uz}\left({\frac{-u^2+uz\cos \theta +u^2+z^2-2uz\cos \theta }{u\sqrt{u^2+z^2-2uz\cos \theta }}|}_0^{\alpha }\right)dz=\\ 2\pi \rho G\frac{z^2}{u^2}\left(\frac{z-u\cos \alpha }{\sqrt{u^2+z^2-2uz\cos \alpha }}+1\right)dz\end{array}}$

Finalmente, integramos respecto de z entre R y R+h

${\displaystyle \Delta g=\frac{2\pi \rho G}{u^2}{\displaystyle \underset{R}{\overset{R+h}{\int }}{z}^2\left(\frac{z-u\cos \alpha }{\sqrt{u^2+z^2-2uz\cos \alpha }}+1\right)dz}}$

Llamando x=z/u=z/(R+h)

${\displaystyle \Delta g=2\pi \rho G\left(R+h\right){\displaystyle \underset{R/(R+h)}{\overset{1}{\int }}{x}^2\left(\frac{x-\cos \alpha }{\sqrt{1+x^2-2x\cos \alpha }}+1\right)dx}}$

Llamando k=αR/h

${\displaystyle \Delta g=2\pi \rho Gh\left(1+\frac{k}{\alpha }\right){\displaystyle \underset{k/(k+\alpha )}{\overset{1}{\int }}{x}^2\left(\frac{x-\cos \alpha }{\sqrt{1+x^2-2x\cos \alpha }}+1\right)dx}}$

Esta integral se resuelve numéricamente utilizando la función integral de MATLAB

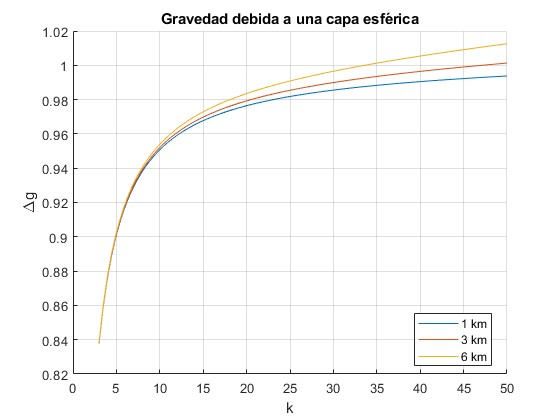
Representamos gráficamente

${\displaystyle \frac{\Delta g}{2\pi G\rho h}=f(k)}$

para las alturas de la planicie, h=1 km, 3 km y 6 km

R=6378; %radio de la Tierra e km
hold on
kk=linspace(3,50,100);
g=zeros(1,length(kk));
for h=[1,3,6] %altura en km
    i=1;
    for k=kk
        a=h*k/R;
        f=@(x) (x.^2).*(1+(x-cos(a))./sqrt(1+x.^2-2*x*cos(a)));
        g(i)=(1+k/a)*integral(f,k/(k+a),1);
        i=i+1;
    end
    plot(kk,g)
end
hold off
grid on
xlabel('k')
legend('1 km','3 km','6 km','location','best')
ylabel('\Deltag')
title('Gravedad debida a una capa esférica')

Aceleración de la gravedad en lo alto de una montaña

Cuando subimos a una montaña nos alejamos del centro de la Tierra, la aceleración de la gravedad disminuye. Por otra parte, la masa bajo nuestro pies se incrementa, aumentado la fuerza de atracción sobre la unidad de masa, la aceleración de la gravedad es mayor

${\displaystyle g=g_0\left(1-2\frac{h}{R}\right)+2\pi G\rho h·f(k)}$

Donde f(k) es el factor de forma de la montaña, que hemos representado gráficamente para modelos simples

${\displaystyle \frac{g-g_0}{g_0}=\left(-\frac{2}{R}+\frac{2\pi G\rho f(k)}{g_0}\right)h}$

Datos:

• Masa de la Tierra, M=5.98·10²⁴ kg
• Radio de la Tierra (ecuatorial), R=6 378 km
• Constante G= 6.67·10^-11 Nm²/kg²

La aceleración de la gravedad en la superficie de la Tierra en reposo (sin movimiento de rotación), supuesta una esfera homogénea

${\displaystyle g_0=\frac{GM}{R^2}=\text{9}\text{.8052}{\text{m/s}}^{\text{2}}}$

La densidad media de la Tierra es

${\displaystyle \rho =\frac{M}{\frac{4}{3}\pi R^2}=\text{ 5}\text{025}{\text{kg/m}}^{\text{3}}}$

Esta densidad es mayor que la de la corteza terrestre, ρ=2700 kg/m³

Teniendo en cuenta que el factor de forma f(k)≈1, es un número próximo a la unidad

${\displaystyle \frac{g-g_0}{g_0}=-\text{1}{\text{.9818·10}}^{-7}h}$

Para que este número sea positivo, la densidad de la montaña tiene que ser mayor

${\displaystyle \begin{array}{l}\frac{2\pi G\rho f(k)}{g_0}\ge \frac{2}{R}\\ \rho \ge \frac{g_0}{\pi GRf(k)}=\text{7}\text{336}\text{.6}{\text{kg/m}}^{\text{3}}=7.3{\text{g/cm}}^{\text{3}}\end{array}}$

Esta densidad es superada por el cobre (8.93), hierro (7.88), oro (19.31), plata (10.5), platino (21.46), etc. Pero es mayor que la del titanio (4.5), aluminio (2.7), silicio (2.3 g/cm³), etc.

Referencias

Ugo Besson. How does weight depend on montain altitude?. Eur. J. Phys. 27 (2006), pp. 743-753