Una superficie equipotencial

Un objeto situado sobre la superficie de la Tierra a una latitud λ, describe un movimiento circular de radio x=r·cosλ tal como se muestra en la figura.

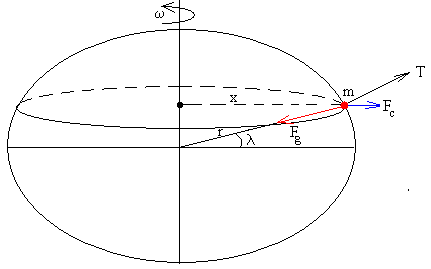
Las fuerzas que actúan sobre dicho objeto desde el punto de vista de un observador no inercial que se mueve con la Tierra son:

• La fuerza de atracción gravitatoria, F_g que tiene dirección radial, y sentido hacia el centro de la Tierra y vale

${\displaystyle F_g=G\frac{Mm}{r^2}}$

siendo r la distancia entre el objeto y el centro de la Tierra, M la masa de la Tierra y G la constante de la gravitación..

• La fuerza centrífuga, F_c cuya dirección es a lo largo del radio de la circunferencia que describe y hacia afuera.

F_c=mω²x

siendo ω la velocidad angular constante de rotación de la Tierra.

La resultante de ambas fuerzas es la tensión T de la cuerda que sujeta la partícula de masa m.

Fuerzas conservativas. Energías potenciales

La fuerza de atracción F_g es conservativa y su energía potencial es

${\displaystyle E_g=-G\frac{Mm}{r}}$

De nuevo, se supone que la Tierra es aproximadamente esférica, y no se tiene en cuenta el abultamiento producido en el ecuador como consecuencia del movimiento de rotación de la Tierra.

La fuerza centrífuga depende únicamente de la distancia x al eje de rotación es por tanto, una fuerza conservativa, cuya energía potencial es

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}m{\omega }^{2}x}·dx=E_c(0)-E_c(x)}$

Tomando el nivel cero de la energía potencial en el eje de rotación x=0.

${\displaystyle E_c(x)=-\frac{1}{2}m{\omega }^2{x}^2=-\frac{1}{2}m{\omega }^2{r}^2{\cos }^2\lambda }$

La energía potencial total es la suma de ambas contribuciones

${\displaystyle E_p(r)=-\frac{1}{2}m{\omega }^2{r}^2{\cos }^2\lambda -G\frac{Mm}{r}}$

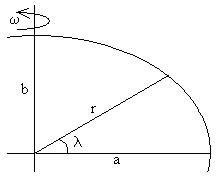
La forma de la Tierra es la de una superficie equipotencial, ya que la dirección vertical o la dirección de la intensidad de la gravedad efectiva $\overrightarrow{g}$ es perpendicular a la superficie equipotencial en cada punto de dicha superficie.

Sea r=b, cuando λ=π/2, la energía potencial vale E_p=-GMm/b. Así que el valor de b determina la superficie equipotencial que describe la forma de la superficie de la Tierra.

${\displaystyle r^3{\cos }^2\lambda -\frac{2GM}{{\omega }^{2}b}r+\frac{2GM}{{\omega }^2}=0}$.

Sea r=a, cuando λ=0. La raíz de la ecuación cúbica determina a en función de b, G, M y ω.

${\displaystyle a^3-\frac{2GM}{{\omega }^{2}b}a+\frac{2GM}{{\omega }^2}=0}$

Conocido b calculamos a resolviendo la ecuación cúbica.

En la siguiente tabla, se proporcionan los datos relativos a la masa en kg, periodo de rotación en horas, y los valores de los radios a (ecuatorial) y b (polar) de algunos planetas del Sistema Solar.

Con el dato de G=6.67·10^-11 Nm²/kg², la velocidad angular de rotación de la Tierra es

${\displaystyle \omega =\frac{2\pi }{23.93·3600}=7.293·{10}^{-5}\text{rad/s}}$

Para facilitar el cálculo en el ordenador, expresamos la distancia en unidades de 10⁶ m. La ecuación que nos permite calcular a a partir del valor observado de b=6.356 es

a³-23594.12a+149964.23=0

Para calcular las raíces de esta ecuación cúbica sugerimos dos procedimientos:

Raíces de una ecuación cúbica

function esferoide_3
    M=0.598e25; %masa de la Tierra
    G=6.67e-11; %constante G
    w=2*pi/(23.93*3600); %velocidad angular de rotación
    b=6.356; %semieje b en 10^6 m
    p1=2*G*M*1e-18/(w^2*b);
    p0=2*G*M*1e-18/w^2;
    raiz=raices_3([1,0,-p1,p0]);
    disp(raiz)

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

 -156.6882
  150.3213
    6.3669

La raíz buscada es a=6.3669·10⁶ m

Alternativamente, se puede utilizar la función roots de MATLAB en vez de la función raices_3

Procedimiento iterativo

Esta ecuación se puede transformar en esta otra equivalente

${\displaystyle a=\frac{a^3+149964.23}{23594.12}}$

para hallar la raíz por el método de iteración partiendo de un valor inicial próximo a 6, obteniendo el valor a=6.367.

x0=6;
while(1)
    x1=(x0*x0*x0+149964.23)/23594.12;
    if abs(x1-x0)<0.001    
        break;
    end
    x0=x1;
end
disp(x0)

    6.3669

Forma del planeta

En la segunda ecuación despejamos 2GM/ω²

${\displaystyle \begin{array}{l}{a}^3-\frac{2GM}{{\omega }^{2}b}a+\frac{2GM}{{\omega }^2}=0\\ \frac{2GM}{{\omega }^2}=\frac{a^{3}b}{a-b}\end{array}}$

Sustituimos en la primera

${\displaystyle r^3{\cos }^2\lambda -\frac{1}{b}\left(\frac{a^{3}b}{a-b}\right)r+\frac{a^{3}b}{a-b}=0}$

Conocidos los semiejes a y b, dado el ángulo 0≤λ<π/2 calculamos la raíz real de la ecuación cúbica en r

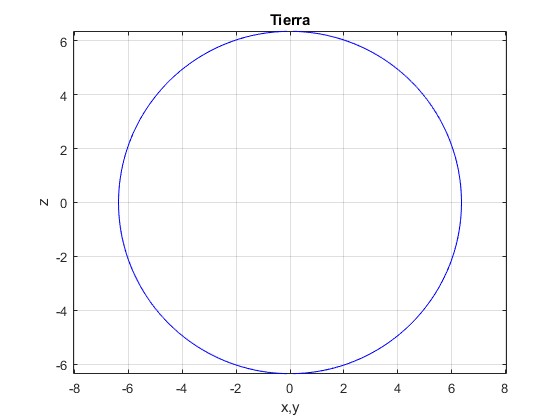
Representamos la forma del planeta calculado la abscisa x=r·cosλ y la ordenada y=r·sinλ de cada punto (color rojo)

Comparamos con la ecuacion de la elipse (color azul)

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

Vemos que coinciden. Calculando el primer cuadrante, extendemos la representación gráfica a los tres restantes

function esferoide_2
    M=0.598e25; %masa de la Tierra
    G=6.67e-11; %constante G
    w=2*pi/(23.93*3600); %velocidad angular de rotación
    b=6.356; %semieje b en 10^6 m
    p1=2*G*M*1e-18/(w^2*b);
    p0=2*G*M*1e-18/w^2;
    raiz=roots([1,0,-p1,p0]);
    a=raiz(3);
    z=@(x) b*sqrt(1-x.^2/a^2);
    fp=fplot(z,[0,a]);
    plot(fp.XData, fp.YData, 'r', fp.XData, -fp.YData,'r', -fp.XData,
 fp.YData,'r', -fp.XData, -fp.YData, 'r')
    Th=(0:89)*pi/180;
    xx=zeros(1,length(Th));
    yy=zeros(1,length(Th));
    k=1;
    for th=Th
        p1=-a^3/((a-b)*cos(th)^2);
        p0=a^3*b/((a-b)*cos(th)^2);
        raiz=roots([1,0,p1,p0]);
        xx(k)=raiz(3)*cos(th);
        yy(k)=raiz(3)*sin(th);
        k=k+1;
    end
    plot(xx,yy,'b',-xx,yy,'b', xx,-yy,'b',-xx,-yy,'b')
    hold off
    grid on
    axis equal
    xlabel('x,y')
    ylabel('z')
    title('Tierra')
end

Otra ecuación que describe la forma de la Tierra

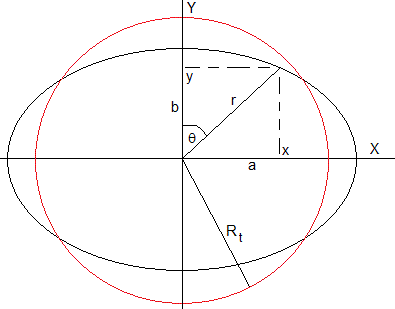
La ecuación de la elipse es

${\displaystyle \begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ \frac{r^2{\sin }^2\theta }{a^2}+\frac{r^2{\cos }^2\theta }{b^2}=1\end{array}}$

Se define el coeficiente de achatamiento f

${\displaystyle f=\frac{a-b}{a}}$

Para la Tierra a=6 378 137 m y b=6 356 752 m, lo que da un coeficiente f=3.35·10^-3

La ecuación de la elipse se convierte en

${\displaystyle \begin{array}{l}{r}^2=\frac{a^2{\left(1-f\right)}^2}{{\cos }^2\theta +{\left(1-f\right)}^2{\sin }^2\theta }=\frac{a^2{\left(1-f\right)}^2}{{\left(1-f{\sin }^2\theta \right)}^2+f^2{\sin }^2\theta {\cos }^2\theta }\\ \frac{r}{a}=\frac{1-f}{1-f{\sin }^2\theta }\frac{1}{\sqrt{1+\frac{f^2{\sin }^2\theta {\cos }^2\theta }{{\left(1-f{\sin }^2\theta \right)}^2}}}\end{array}}$

Teniendo en cuenta que para la Tierra f es muy pequeño

${\displaystyle \begin{array}{l}\frac{r}{a}\approx \frac{1-f}{1-f{\sin }^2\theta }\left(1-\frac{1}{2}\frac{f^2{\sin }^2\theta {\cos }^2\theta }{{\left(1-f{\sin }^2\theta \right)}^2}\right)\\ \frac{r}{a}\approx \frac{1-f}{1-f{\sin }^2\theta }\approx \left(1-f\right)\left(1+f{\sin }^2\theta +\mathrm{...}\right)\approx 1-f\left(1-{\sin }^2\theta \right)=1-f{\cos }^2\theta \end{array}}$

>> syms x;
>> taylor(1/sqrt(1+x^2),x)
ans =(3*x^4)/8 - x^2/2 + 1
>> taylor(1/(1-x),x)
ans =x^5 + x^4 + x^3 + x^2 + x + 1

La definción del polinomio P₂(x) de Legendre

${\displaystyle \begin{array}{l}{P}_2\left(\cos \theta \right)=\frac{1}{2}\left(3{\cos }^2\theta -1\right)\\ \frac{r}{a}\approx 1-\frac{f}{3}-\frac{2}{3}f{P}_2\left(\cos \theta \right)\end{array}}$

El radio medio de la esfera equivalente, se obtiene igualando el volumen del elipsoide de revolución de semiejes a y b con el volumen de una esfera de radio R_t

${\displaystyle \begin{array}{l}\frac{4}{3}\pi R_t^3=\frac{4}{3}\pi a^{2}b\\ R_t^3=a^3\left(1-f\right)\\ R_t=a{\left(1-f\right)}^{1/3}\approx a\left(1-\frac{f}{3}\right)\end{array}}$

La ecuación de la forma del planeta se escribe

${\displaystyle \begin{array}{l}r\approx a\left(1-\frac{f}{3}\right)-\frac{2}{3}af{P}_2\left(\cos \theta \right)\\ r\approx R_t\left(1-\frac{2}{3}f{P}_2\left(\cos \theta \right)\right)\\ r\approx R_t\left(1+\frac{1}{3}f-f{\cos }^2\theta \right)\end{array}}$

Esta es la primera aproximación a la forma de la Tierra. La segunda ecuación, expresada en términos del polinomio de Legendre, nos será útil para calcular la energía potencial producida por un esferoide homogéneo

El semieje mayor a, se obtiene para θ=π/2 y el b, para θ=0

${\displaystyle \begin{array}{l}b\approx R_t\left(1+\frac{1}{3}f-f\right)=R_t\left(1-\frac{2}{3}f\right)\\ a\approx R_t\left(1+\frac{1}{3}f\right)\end{array}}$

Comparamos la ecuación de la elipse con la expresión polar aproximada, para f=0.1 y 0.3, tomando R_t=1

${\displaystyle \begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ r\approx R_t\left(1+\frac{1}{3}f-f{\cos }^2\theta \right),\{\begin{array}{l}x=r\sin \theta \\ y=r\cos \theta \end{array}\\ f=\frac{a-b}{a},R_t={\left(a^{2}b\right)}^{1/3}\end{array}}$

Rt=1;
f=0.1;
r=@(th) Rt*(1-f*cos(th).^2+f/3);
hold on
fplot(@(th) r(th).*sin(th), @(th) r(th).*cos(th),[0,2*pi] )
a=Rt*(1+f/3);
b=Rt*(1-2*f/3);
z=@(x) b*sqrt(1-x.^2/a^2);
fp=fplot(z,[0,a]);
plot(fp.XData, fp.YData, 'r', fp.XData, -fp.YData, 'r', -fp.XData,
 fp.YData, 'r', -fp.XData, -fp.YData, 'r')
hold off
grid on
axis equal
xlabel('x,y')
ylabel('z')
title('esferoide')

Para f=0.3, hay diferencia

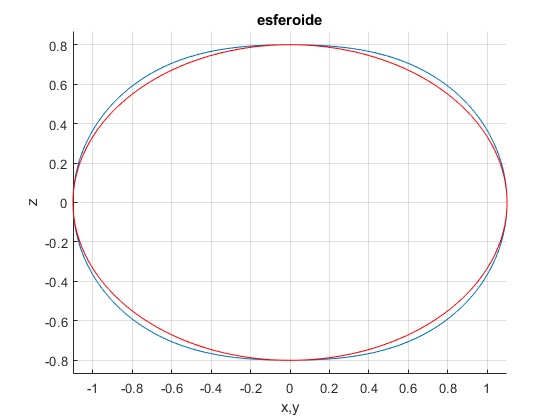
Para f=0.1, casi coinciden

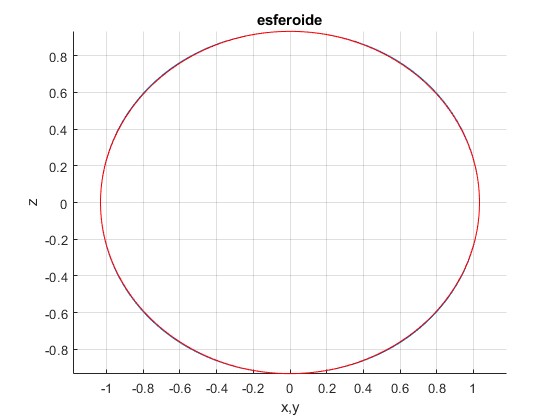
En el caso de la Tierra a=6 378 137 m y b=6 356 752 m

a=6378137/1e6;
b=6356752/1e6; %en unidades 10^6 m
Rt=(a^2*b)^(1/3); %radio medio de la esfera equivalente
f=(a-b)/a; %achatamiento
r=@(th) Rt*(1-f*cos(th).^2+f/3);
hold on
fplot(@(th) r(th).*sin(th), @(th) r(th).*cos(th),[0,2*pi] ) %aproximada
%circunfeencia de radio Rt
fplot(@(th) Rt*sin(th), @(th) Rt*cos(th),[0,2*pi],'lineStyle','--' )
%circunfeencia de radio Rt
a=Rt*(1+f/3);
b=Rt*(1-2*f/3);
z=@(x) b*sqrt(1-x.^2/a^2);
fp=fplot(z,[0,a]);
plot(fp.XData, fp.YData, 'r', fp.XData, -fp.YData, 'r', -fp.XData, 
fp.YData, 'r', -fp.XData, -fp.YData, 'r') %elipse
hold off
grid on
axis equal
xlabel('x,y, 10^6 m')
ylabel('z, 10^6 m')
title('Tierra')

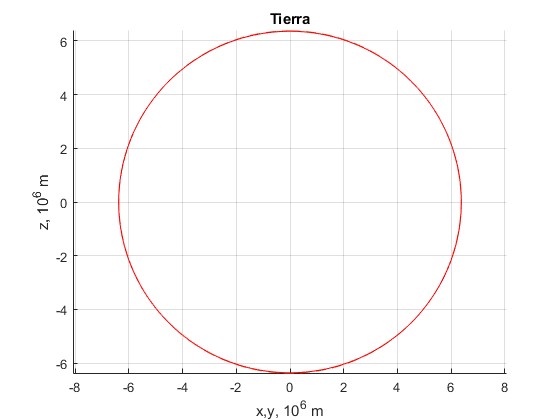
La Tierra se desvía muy poco de la forma esférica. Utilizando varias veces la herramienta Zoom podremos ver la diferencia entre la circunferencia de radio R_t y la elipse de semiejes a y b

Referencias

Bolemon. Shape of the rotating planets and the Sun: A calculation for elementary mechanics. Am. J. Phys. 44 (11) November 1976, pp. 1125-1128.

William Lowrie. A Student’s Guide to Geophysical Equations. Cambridge University Press, (2011), pp. 86-90