La Tierra considerada como una esfera de radio R.

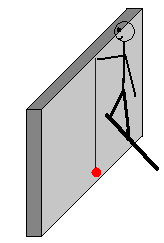
Debido a la rotación de la Tierra, la dirección radial no coincide con la dirección vertical, o con la dirección de la plomada, que es una cuerda de la que pende un trozo de plomo que utilizan los albañiles para comprobar la verticalidad de las paredes que construyen.

Supongamos una masa puntual m que cuelga de una cuerda, situada en un lugar del hemisferio norte cuya latitud es λ. La Tierra gira sobre su eje con velocidad angular constante ω. La partícula describe una circunferencia de radio R·cos λ, siendo R el radio de la Tierra para un observador inercial

La resultante de las fuerzas que actúan sobre la partícula deberá se igual al producto de la masa por la aceleración normal a_n=ω²R·cos λ, y estará dirigida hacia el centro de la circunferencia que describe la partícula.

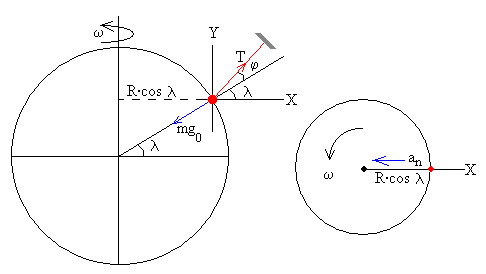
Las fuerzas que actúan sobre la partícula son:

• La fuerza de atracción de la Tierra, que tiene dirección radial y está dirigida hacia su centro, y cuyo módulo es

${\displaystyle F_g=G\frac{mM}{R^2}=m{g}_0}$

• La tensión T de la cuerda que sujeta a la partícula, y que forma un ángulo φ con la dirección radial, tal como se aprecia en la figura.

La partícula está en equilibrio a lo largo del eje Y.

T·sin(λ+φ)-mg₀·sinλ=0

La partícula tiene una aceleración a_n a lo largo del eje X.

Tcos(λ+φ)- mg₀·cosλ=-mω²R·cos λ

Eliminando T en el sistema de dos ecuaciones, obtenemos

${\displaystyle \tan (\lambda +\phi )=\frac{\tan \lambda }{1-\alpha }\alpha =\frac{R{\omega }^2}{g_0}=3.45·{10}^{-3}}$        (1)

donde hemos tomado R=6.37·10⁶ m, ω=2π/(23.93·60·60) rad/s, y g₀=9.81 m/s²

Después de algunas operaciones trigonométricas, despejamos el ángulo φ que forma la plomada con la dirección radial

${\displaystyle \tan \phi =\frac{\alpha \tan \lambda }{1-\alpha +{\tan }^2\lambda }}$

Como α es pequeño frente a la unidad, el ángulo φ es pequeño

${\displaystyle \phi \approx \tan \phi \approx \frac{\alpha }{2}\sin (2\lambda )}$

A la latitud correspondiente al norte de España, algo más de λ=43º, tenemos que φ=0.099º. Este resultado hay que corregirlo si la Tierra se condera un elipsoide de revolución de semiejes a=6 378 137 m (radio ecuatorial) y b=6 356 752 m

Energía potencial de un esferoide

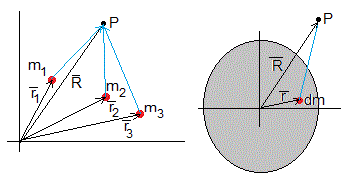
La energía potencial producida en el punto P, situado en la posición $\overrightarrow{R}$, por las masas puntales m₁ situada en la posición $\overrightarrow{r_1}$, m₂ situada en la posición $\overrightarrow{r_2}$, m₃ situada en la posición $\overrightarrow{r_3}$, es

${\displaystyle E_p\left(\overrightarrow{R}\right)=-G\frac{m_1}{\left|\overrightarrow{R}-\overrightarrow{r_1}\right|}-G\frac{m_2}{\left|\overrightarrow{R}-\overrightarrow{r_2}\right|}-G\frac{m_3}{\left|\overrightarrow{R}-\overrightarrow{r_3}\right|}=-G{\displaystyle \sum _{k=1}^N\frac{m_k}{\left|\overrightarrow{R}-\overrightarrow{r_k}\right|}}}$

Para una distribución continua de masa

${\displaystyle E_p\left(\overrightarrow{R}\right)=-G{\displaystyle \underset{V}{\int }\frac{dm}{\left|\overrightarrow{R}-\overrightarrow{r}\right|}}=-G{\displaystyle \underset{V}{\int }\frac{\rho \left(\overrightarrow{r}\right)}{\left|\overrightarrow{R}-\overrightarrow{r}\right|}}dV}$

Donde ρ es la densidad en la posición $\overrightarrow{r}$ de la distribución de masas y dV es un elemento diferencial de volumen alrededor de dicho punto

En coordenadas esféricas

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=r\sin \theta ·\cos \phi \\ y=r\sin \theta ·\sin \phi \\ z=r\cos \theta \end{array}\\ dV=dx·dy·dz=r^2\sin \theta ·dr·d\theta ·d\phi \end{array}}$

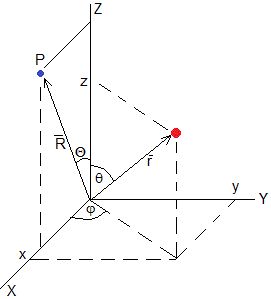
Vamos a suponer que la densidad no depende del ángulo φ, solamente ρ(r,θ). Por lo que podemos situar el punto P cuya posición es $\overrightarrow{R}$ en el plano XY

La energía potencial producida por la distribución de masa en P es

${\displaystyle \begin{array}{l}{E}_p\left(\overrightarrow{R}\right)=-G{\displaystyle \underset{V}{\iint }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\rho \left(r,\theta \right)}{\left|\overrightarrow{R}-\overrightarrow{r}\right|}{r}^2\sin \theta ·dr·d\theta ·d\phi }}\\ \overrightarrow{R}=R\sin \Theta \widehat{i}+R\cos \Theta \widehat{k}\\ \overrightarrow{r}=r\sin \theta \cos \phi \widehat{i}+r\sin \theta \sin \phi \widehat{j}+r\cos \theta \widehat{k}\end{array}}$

En la figura, se muestra el elemento diferencial de volumen dV alrededor del punto de coordenadas (r, θ, φ)

${\displaystyle \begin{array}{l}\left|\overrightarrow{R}-\overrightarrow{r}\right|=\sqrt{{\left(R\sin \Theta -r\sin \theta \cos \phi \right)}^2+{\left(-r\sin \theta \sin \phi \right)}^2+{\left(R\cos \Theta -r\cos \theta \right)}^2}=\\ \sqrt{R^2+r^2-2rR\left(\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \right)}\\ E_p\left(R,\Theta \right)=-G{\displaystyle \underset{V}{\iint }{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\rho \left(r,\theta \right)r^2\sin \theta ·dr·d\theta {\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{R\sqrt{1+\frac{r^2}{R^2}-2\frac{r}{R}\left(\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \right)}}}}}\end{array}}$

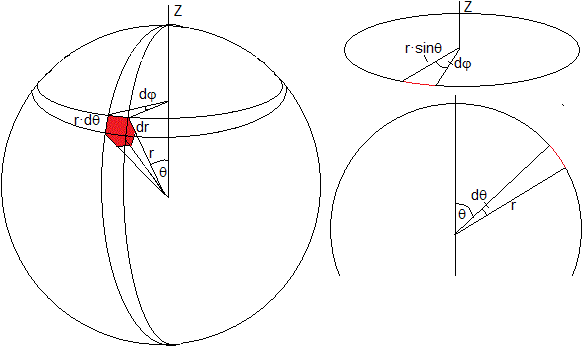
Desarrollamos en serie el término bajo la raíz cuadrada

>> syms t x;
>> taylor(1/sqrt(1+t^2-2*t*x),t,'Order',4)
ans =((5*x^3)/2 - (3*x)/2)*t^3 + ((3*x^2)/2 - 1/2)*t^2 + x*t + 1

Donde hemos designado x a F y t al cociente r/R

${\displaystyle \begin{array}{l}F=\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \\ E_p\left(R,\Theta \right)=-G{\displaystyle \underset{V}{\iint }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\rho \left(r,\theta \right)r^2\sin \theta ·dr·d\theta \frac{1}{R}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(1+\frac{r}{R}F+\frac{1}{2}\left(3F^2-1\right)\frac{r^2}{R^2}+\frac{1}{2}\left(5F^3-3F\right)\frac{r^3}{R^3}+\mathrm{...}\right)d\phi }}}\end{array}}$

Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos \phi d\phi }=0\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}{\cos }^2\phi d\phi }=\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}{\cos }^3\phi d\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(1-{\sin }^2\phi \right)\cos \phi d\phi ={\sin \phi -\frac{1}{3}{\sin }^3\phi |}_0^{2\pi }}=0\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}Fd\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \right)}d\phi =2\pi \cos \Theta \cos \theta \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}{F}^{2}d\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left(\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \right)}^2}d\phi =\pi {\sin }^2\Theta {\sin }^2\theta +2\pi {\cos }^2\Theta {\cos }^2\theta =\\ 2\pi \left\{\frac{1}{3}+\frac{2}{3}\left(\frac{3}{2}{\cos }^2\Theta -\frac{1}{2}\right)\left(\frac{3}{2}{\cos }^2\theta -\frac{1}{2}\right)\right\}\\ \frac{1}{2}\left({\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(3F^2-1\right)d\phi }\right)=2\pi \left\{1+2\left(\frac{3}{2}{\cos }^2\Theta -\frac{1}{2}\right)\left(\frac{3}{2}{\cos }^2\theta -\frac{1}{2}\right)-1\right\}=\\ \frac{1}{2}\left(3{\cos }^2\Theta -1\right)\frac{1}{2}\left(3{\cos }^2\theta -1\right)\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}{F}^{3}d\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left(\sin \Theta \sin \theta \cos \phi +\cos \Theta \cos \theta \right)}^3}d\phi =2\pi {\cos }^3\Theta {\cos }^3\theta +3\pi {\sin }^2\Theta {\sin }^2\theta \cos \Theta \cos \theta \\ \frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(5F^3-3F\right)d\phi }=\frac{2\pi }{2}\left\{5\left({\cos }^3\Theta {\cos }^3\theta +\frac{3}{2}\left(1-{\cos }^2\Theta \right)\left(1-{\cos }^2\theta \right)\cos \Theta \cos \theta \right)-3\cos \Theta \cos \theta \right\}=\\ 2\pi \frac{1}{2}\left(5{\cos }^3\Theta -3\cos \Theta \right)\frac{1}{2}\left(5{\cos }^3\theta -3\cos \theta \right)\end{array}}$

La energía potencial en el punt P se expresa

${\displaystyle \begin{array}{l}{E}_p\left(R,\Theta \right)=-G{\displaystyle \underset{V}{\iint }\rho \left(r,\theta \right)r^2\sin \theta ·dr·d\theta \frac{2\pi }{R}\left\{1+\cos \Theta \cos \theta \frac{r}{R}+\frac{1}{2}\left(3{\cos }^2\Theta -1\right)\frac{1}{2}\left(3{\cos }^2\theta -1\right)\frac{r^2}{R^2}+\frac{1}{2}\left(5{\cos }^3\Theta -3\cos \Theta \right)\frac{1}{2}\left(5{\cos }^3\theta -3\cos \theta \right)\frac{r^3}{R^3}+\mathrm{...}\right\}}\\ E_p\left(R,\Theta \right)=-G\frac{2\pi }{R}{\displaystyle \underset{V}{\iint }\rho \left(r,\theta \right)\left\{1+P_1\left(\cos \Theta \right)P_1\left(\cos \theta \right)\frac{r}{R}+P_2\left(\cos \Theta \right)P_2\left(\cos \theta \right)\frac{r^2}{R^2}+P_3\left(\cos \Theta \right)P_3\left(\cos \theta \right)\frac{r^3}{R^3}+\mathrm{...}\right\}{r}^2\sin \theta ·dr·d\theta }\end{array}}$

De otra forma

${\displaystyle \begin{array}{l}{E}_p\left(R,\Theta \right)=-G\frac{2\pi }{R}{\displaystyle \sum _{n=0}^{\infty }{\Phi }_n(R)P_n}\left(\cos \Theta \right)\\ {\Phi }_n(R)=\frac{1}{R^n}{\displaystyle \underset{V}{\iint }{r}^{n+2}\rho \left(r,\theta \right)P_n\left(\cos \theta \right)\sin \theta ·dr·d\theta }\end{array}}$

Esfera de densidad uniforme

El caso más sencillo, es una esfera uniforme (densidad constante) de radio R_t.

Teniendo en cuenta que que el área bajo el polinomio de Legendre, P_n(x) entre -1 y +1 es nula salvo la de P₀(x)=1

${\displaystyle \begin{array}{l}{\Phi }_n(R)=\frac{\rho }{R^n}{\displaystyle \underset{0}{\overset{R}{\int }}{r}^{n+2}dr{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)\sin \theta ·d\theta =}}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)\sin \theta ·d\theta =-}{\displaystyle \underset{1}{\overset{-1}{\int }}{P}_n(x)dx={\displaystyle \underset{-1}{\overset{1}{\int }}{P}_n(x)dx}=\{\begin{array}{l}\mathrm{2,}n=0\\ \mathrm{0,}n\ge 1\end{array}}\\ {\Phi }_0(R)=2\rho {\displaystyle \underset{0}{\overset{R_t}{\int }}{r}^{2}dr=\frac{2}{3}}\rho R_t^3\end{array}}$

El resultado es el esperado

${\displaystyle \begin{array}{l}{E}_p\left(R,\Theta \right)=-G\frac{2\pi }{R}{\displaystyle \sum _{n=0}^{\infty }{\Phi }_n(R)P_n}\left(\cos \Theta \right)=-G\frac{2\pi }{R}{\Phi }_0(R)P_0\left(\cos \Theta \right)=-G\frac{2\pi }{R}\left(\frac{2}{3}\frac{M}{\frac{4}{3}\pi R_t^3}{R}_t^3\right)\\ E_p\left(R,\Theta \right)=-\frac{GM}{R}\end{array}}$

Elipsoide de revolución

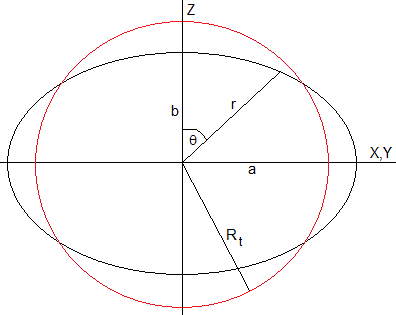
Se obtiene el elipsoide de revolución girando la elipse de la figura alrededor del eje Z

En la página titulada La forma de la Tierra, obtuvimos la ecuación en coordenadas polares de una elipse de semiejes a y b muy próxima a una circunferencia de radio R_t que es el caso de la Tierra

${\displaystyle \begin{array}{l}r=R_t\left(1-\frac{2}{3}\epsilon P_2\left(\cos \theta \right)\right)=R_t\left(1-\frac{1}{3}\epsilon \left(3{\cos }^2\theta -1\right)\right)\\ b=R_t\left(1-\frac{2}{3}\epsilon \right),\theta =0\\ a=R_t\left(1+\frac{1}{3}\epsilon \right),\theta =\frac{\pi }{2}\\ f=\frac{a-b}{R_t}\end{array}}$

donde f mide el achatamiento

Teniendo en cuenta la relación de ortogonalidad de los polinomios de Legendre

${\displaystyle {\displaystyle \underset{-1}{\overset{1}{\int }}{P}_n(x)P_m(x)dx=-{\displaystyle \underset{\pi }{\overset{0}{\int }}{P}_n\left(\cos \theta \right)P_m\left(\cos \theta \right)\sin \theta ·d\theta }}={\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)P_m\left(\cos \theta \right)\sin \theta ·d\theta }\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{2}{2n+1},m=n\end{array}}$

Calculamos primero Φ_n(R)

${\displaystyle \begin{array}{l}{\Phi }_n(R)=\frac{\rho }{R^n}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)\sin \theta ·d\theta {\displaystyle \underset{0}{\overset{R_t\left(1-\frac{2}{3}f{P}_2\left(\cos \theta \right)\right)}{\int }}{r}^{n+2}dr}}\\ {\Phi }_n(R)=\frac{\rho }{R^n}\frac{R_t^{n+3}}{n+3}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right){\left(1-\frac{2}{3}f{P}_2\left(\cos \theta \right)\right)}^{n+3}\sin \theta ·d\theta }\\ {\Phi }_n(R)\approx \frac{\rho }{R^n}\frac{R_t^{n+3}}{n+3}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)\left(1-\frac{2}{3}\left(n+3\right)f{P}_2\left(\cos \theta \right)\right)\sin \theta ·d\theta }\\ {\Phi }_n(R)\approx \frac{\rho }{R^n}\frac{R_t^{n+3}}{n+3}\left\{{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)P_0\left(\cos \theta \right)\sin \theta ·d\theta -\frac{2}{3}\left(n+3\right)f{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n\left(\cos \theta \right)P_2\left(\cos \theta \right)}\sin \theta ·d\theta }\right\}\\ {\Phi }_0(R)\approx \frac{\rho }{R^0}\frac{R_t^3}{0+3}\left\{2\right\}=\frac{2}{3}\rho R_t^3=\frac{M}{2\pi }\\ {\Phi }_1(R)\approx 0\\ {\Phi }_2(R)\approx \frac{\rho }{R^2}\frac{R_t^{2+3}}{2+3}\left\{-\frac{2}{3}\left(2+3\right)f\frac{2}{5}\right\}=-\frac{4}{15}\rho f\frac{R_t^5}{R^2}=-\frac{M}{5\pi }\frac{R_t^2}{R^2}f\\ {\Phi }_n(R)\approx \mathrm{0,}n\ge 3\end{array}}$

La energía potencial en el punto P producida por el elipsoide homogéneo vale

${\displaystyle \begin{array}{l}{E}_p\left(R,\Theta \right)=-G\frac{2\pi }{R}{\displaystyle \sum _{n=0}^{\infty }{\Phi }_n(R)P_n}\left(\cos \Theta \right)\\ E_p\left(R,\Theta \right)\approx -G\frac{2\pi }{R}\left\{{\Phi }_0(R)P_0\left(\cos \Theta \right)+{\Phi }_2(R)P_2\left(\cos \Theta \right)\right\}=\\ -G\frac{2\pi }{R}\left\{\frac{M}{2\pi }{P}_0\left(\cos \Theta \right)-\frac{M}{5\pi }f\frac{R_t^2}{R^2}{P}_2\left(\cos \Theta \right)\right\}\\ E_p\left(R,\Theta \right)\approx -G\frac{M}{R}\left(1-\frac{2}{5}f\frac{R_t^2}{R^2}{P}_2\left(\cos \Theta \right)\right)\\ E_p\left(R,\Theta \right)\approx -G\frac{M}{R_t}\left(\frac{R_t}{R}-\frac{a_2}{2}\frac{R_t^3}{R^3}\left(3{\cos }^2\Theta -1\right)\right)\end{array}}$

El coeficiente a₂=1.082 635·10^-3 se ha medido con mucha precisión por medio de satélites en órbita

La aceleración de la gravedad

La aceleración de la gravedad es

${\displaystyle \begin{array}{l}\overrightarrow{g_0}=-\frac{\partial E_p}{\partial R}\widehat{r}-\frac{1}{R}\frac{\partial E_p}{\partial \Theta }\widehat{\theta }=\\ -G\frac{M}{R_t^2}\left(\frac{R_t^2}{R^2}-\frac{3a_2}{2}\frac{R_t^4}{R^4}\left(3{\cos }^2\Theta -1\right)\right)\widehat{r}+G\frac{M}{R_t^2}\left(\frac{3a_2}{2}\frac{R_t^4}{R^4}\sin \left(2\Theta \right)\right)\widehat{\theta }\end{array}}$

En la componente radial, el segundo término es pequeño frente al primero

El ángulo entre $\overrightarrow{g_0}$ y la dirección radial, es

${\displaystyle \begin{array}{l}\tan {\epsilon }_g=\left|\frac{G\frac{M}{R_t^2}\left(\frac{3a_2}{2}\frac{R_t^4}{R^4}\sin \left(2\Theta \right)\right)}{-G\frac{M}{R_t^2}\left(\frac{R_t^2}{R^2}-\frac{3a_2}{2}\frac{R_t^4}{R^4}\left(3{\cos }^2\Theta -1\right)\right)}\right|\approx \frac{\frac{3a_2}{2}\frac{R_t^4}{R^4}\sin \left(2\Theta \right)}{\frac{R_t^2}{R^2}}\approx \frac{3a_2}{2}\sin \left(2\Theta \right)\\ {\epsilon }_g\approx \tan {\epsilon }_g=\frac{3a_2}{2}\sin \left(2\lambda \right)\end{array}}$

Se ha tenido en cuenta que en la superficie de la Tierra R≈R_t

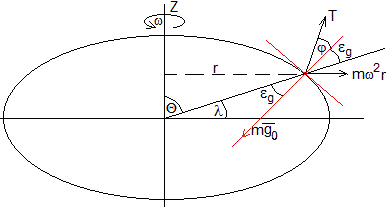
El ángulo que forma la dirección de la plomada con la dirección radial es la suma de dos ángulos. Hemos calculado el ángulo φ al principio de esta página

${\displaystyle \begin{array}{l}{\epsilon }_g+\phi =\frac{3a_2}{2}\sin \left(2\lambda \right)+\frac{\alpha }{2}\sin \left(2\lambda \right)=\frac{1}{2}\left(3a_2+\alpha \right)\sin \left(2\lambda \right),\alpha =\frac{R_t{\omega }^2}{g_0}\\ \frac{1}{2}\left(3a_2+\alpha \right)=\frac{1}{2}\left(3·1.082635·{10}^{-3}+3.45·{10}^{-3}\right)=3.3490·{10}^{-3}\end{array}}$

La suma de los dos términos es similar al coeficiente f de achatamiento

Deducción alternativa

Obtenemos esta expresión sumando la energía potencial gravitatoria y la energía potencial centrífuga

${\displaystyle \begin{array}{l}U\left(R,\Theta \right)=-G\frac{M}{R_t}\left(\frac{R_t}{R}-\frac{a_2}{2}\frac{R_t^3}{R^3}\left(3{\cos }^2\Theta -1\right)\right)-\frac{1}{2}{\omega }^2{R}^2{\cos }^2\left(\frac{\pi }{2}-\Theta \right)=\\ -G\frac{M}{R_t}\left(\frac{R_t}{R}-\frac{a_2}{2}\frac{R_t^3}{R^3}\left(3{\cos }^2\Theta -1\right)\right)-\frac{1}{2}\frac{GM}{R_t^3}\alpha R^2{\sin }^2\Theta \\ U\left(R,\Theta \right)=-G\frac{M}{R_t}\left(\frac{R_t}{R}-\frac{a_2}{2}\frac{R_t^3}{R^3}\left(3{\cos }^2\Theta -1\right)+\frac{\alpha }{2}\frac{R^2}{R_t^2}{\sin }^2\Theta \right)\end{array}}$

La aceleración de la gravedad es

${\displaystyle \begin{array}{l}\overrightarrow{g}=-\frac{\partial U}{\partial R}\widehat{r}-\frac{1}{R}\frac{\partial U}{\partial \Theta }\widehat{\theta }=\\ -G\frac{M}{R_t^2}\left(\frac{R_t^2}{R^2}-\frac{3a_2}{2}\frac{R_t^4}{R^4}\left(3{\cos }^2\Theta -1\right)-\alpha \frac{R}{R_t}{\sin }^2\Theta \right)\widehat{r}+G\frac{M}{R_t^2}\left(\frac{3a_2}{2}\frac{R_t^4}{R^4}\sin \left(2\Theta \right)+\frac{\alpha }{2}\frac{R}{R_t}\sin \left(2\Theta \right)\right)\widehat{\theta }\end{array}}$

Despreciando el segundo y tercer término de la componente radial y haciendo la aproximación R≈R_t

${\displaystyle \begin{array}{l}\epsilon \approx \tan \epsilon =\left|\frac{g_{\theta }}{g_r}\right|=\frac{G\frac{M}{R_t^2}\left(\frac{3a_2}{2}\frac{R_t^4}{R^4}+\frac{\alpha }{2}\frac{R}{R_t}\right)\sin \left(2\Theta \right)}{G\frac{M}{R_t^2}\frac{R_t^2}{R^2}}=\left(\frac{3a_2}{2}\frac{R_t^2}{R^2}+\frac{\alpha }{2}\frac{R^3}{R_t^3}\right)\sin \left(2\Theta \right)\\ \epsilon \approx \frac{1}{2}\left(3a_2+\alpha \right)\sin \left(2\Theta \right)\end{array}}$

Fórmula internacional de la aceleración de la gravedad (1967)

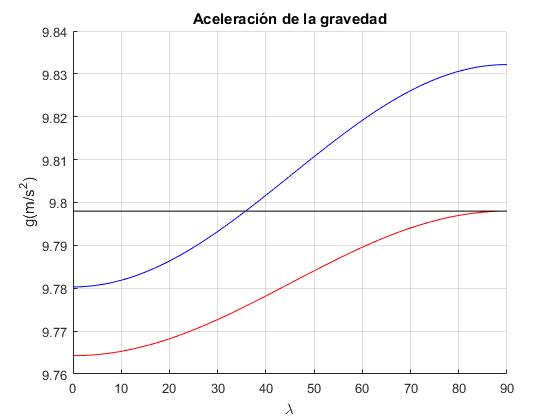
En la figura, se comparan tres expresiones de la aceleración de la gravedad (Véase Gröber 2007):

• En negro, g₀= 9.798 m/s² producido por una esfera homegénea de radio R=6378.137 km (radio ecuatorial) que no gira sobre sí misma.
• En rojo, la misma esfera que gira con velcidad angular ω=7.292 115·10^-5/rad/s

g=g₀-ω²·R·cos²λ

• En azul, la fórmula que tiene en cuenta la rotación de la Tierra y que la Tierra no es una esfera perfecta

g=9.780 3126 772 ·(1+0.005 302 33 ·sin²λ-0.000 005 89· sin²2λ) m/s²

x=linspace(0,pi/2,100);
g=9.7803126772*(1+0.00530233*(sin(x)).^2-0.00000589*(sin(2*x)).^2);
hold on
plot(x*180/pi,g,'b')
gg=9.798-(2*pi/(24*3600))^2*6378137*(cos(x)).^2;
plot(x*180/pi,gg,'r')
line([0,90],[9.798,9.798],'color','k')
hold off
grid on
xlabel('\lambda')
ylabel('g(m/s^2)')
title('Aceleración de la gravedad')

En este script se calcula la aceleración de la gravedad g utilizando esta última expresión, cuando se introduce la latitud λ en grados.

Cuando nos elevamos una altura h sobre el nivel del mar hay que introducir una corrección, que disminuye el valor de g a nivel del mar.

${\displaystyle \Delta g=\frac{2g_{0}h}{R}}$

donde g₀=9.832 m/s² es la aceleración de la gravedad a nivel del mar en los polos, R=6371 km es el radio medio de la Tierra.

Δg= 3.086·10^-6 ·h m/s²

Hay otros términos correctores que tienen en cuenta si el terreno que rodea a la localidad de observación es montañoso o plano. Véase la página 831 del artículo (Nelson, 1981)

La web WolframAlfa computational knowledge engine, nos proporciona los datos de la aceleración de la gravedad y de sus componentes, en base al modelo EGM2008 12th (33 metros por encima del mar). En la imagen los datos de la aceleración de la gravedad en Bilbao

Referencias

Mohazzabi P, James M. Plumb line and the shape of the earth. Am. J. Phys. 68 (11) November 2000, pp. 1038-1041

Iona M. Why is g larger at the poles?. Am. J. Phys. 46 (8) August 1978, pp. 790-791.

Nelson R. A. Determination of the acceleration due to gravity with the Cenco-Behr free-fall apparatus. Am. J. Phys. 49 (9) September 1981, pp. 829-833.

Gröber S., Vetter M., Eckert B, Jodl H-J, World pendulum-a distributed remotely controlled laboratory (RCL) to measure the Earth's gravitational acceleration depending on geometrical latitude. Eur. J. Phys. 28 (2007) 603-613