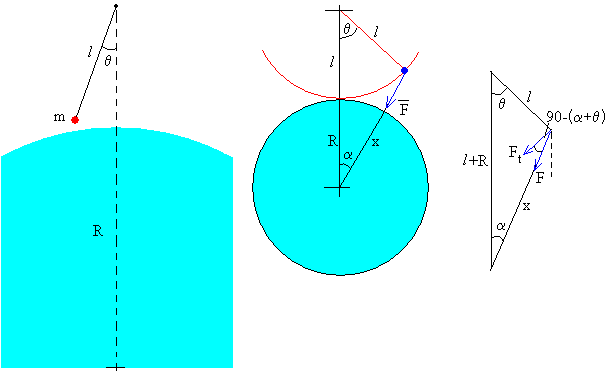
Sea un péndulo simple de longitud l, de cuyo extremo cuelga una masa puntual m. Supondremos que se mueve en el vacío y que está suspendido de un soporte rígido por una cuerda inextensible y de peso despreciable.

Cuando el péndulo forma un ángulo θ con la dirección radial, la fuerza de atracción entre la Tierra y la masa puntual m es

${\displaystyle F=G\frac{Mm}{x^2}=G\frac{Mm}{{(R+l)}^2+l^2-2l(R+l)\cos \theta }}$

La componente F_t de dicha fuerza F a lo largo de la dirección tangencial es

${\displaystyle F_t=F·\text{sin}(\theta +\alpha )=G\frac{Mm}{{(R+l)}^2+l^2-2l(R+l)\cos \theta }\text{sin}(\theta +\alpha )}$

Aplicamos el teorema del seno al triángulo de la figura

${\displaystyle \frac{\text{sin}(180-(\alpha +\theta ))}{l+R}=\frac{\text{sin}\theta }{x}}$

para expresar la componente F_t en función del ángulo θ

${\displaystyle F_t=G\frac{Mm(l+R)}{{\left({(R+l)}^2+l^2-2l(R+l)\cos \theta \right)}^{3/2}}\text{sin}\theta }$

La segunda ley de Newton, afirma que la componente tangencial de la fuerza es igual a la masa por la aceleración tangencial, a_t=l·d²θ/dt².

${\displaystyle \begin{array}{l}l\frac{d^2\theta }{d{t}^2}=-G\frac{M(l+R)}{{\left({(R+l)}^2+l^2-2l(R+l)\cos \theta \right)}^{3/2}}\text{sin}\theta \\ \frac{d^2\theta }{d{t}^2}=-\frac{g(\beta +1)}{l}\frac{\text{sin}\theta }{{\left(1+4\beta (1+\beta ){\text{sin}}^2(\frac{\theta }{2})\right)}^{3/2}}\end{array}}$

con β=l/R y g=GM/R², aceleración de la gravedad en la superficie de la Tierra

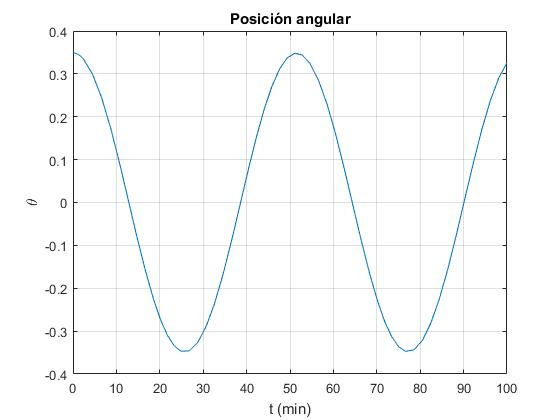
Se resuelve esta ecuación diferencial de segundo orden por procedimiento numéricos con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0.

x0=[20*pi/180,0];
beta=0.5;
f=@(t,x) [x(2);-9.8299*(beta+1.0)*sin(x(1))/
(beta*6.37e6*(1+4*beta*(1+beta)*sin(x(1)/2)^2)^(3/2))]; 
tspan=[0,100*60];
[t,x]=ode45(f,tspan,x0);

plot(t/60,x(:,1))
grid on
xlabel('t (min)')
ylabel('\theta');
title('Posición angular')

Periodo del péndulo

La fuerza de atracción entre la Tierra y la masa puntual m es conservativa. la energía total permanece constante

Igualamos la energía en el instante t=0, cuando el péndulo se desvía de la posición de equilibrio estable un ángulo θ₀, a la energía en el instante t, cuando la posición angular del péndulo es θ, y su velocidad angular dθ/dt.

$$\begin{gathered} {\displaystyle E=\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2-G\frac{Mm}{{\left({(R+l)}^2+l^2-2l(R+l)\cos \theta \right)}^{1/2}}= \\ -G\frac{Mm}{{\left({(R+l)}^2+l^2-2l(R+l)\cos {\theta }_0\right)}^{1/2}}} \end{gathered}$$

Despejamos la velocidad angular dθ/dt.

${\displaystyle \begin{array}{l}\frac{1}{2}{l}^2{\left(\frac{d\theta }{dt}\right)}^2-\frac{gR}{{\left(1+2\beta (1+\beta )(1-\cos \theta )\right)}^{1/2}}=-\frac{gR}{{\left(1+2\beta (1+\beta )(1-\cos {\theta }_0)\right)}^{1/2}}\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{2g}{\beta l}\left\{\frac{1}{{\left(1+4\beta (1+\beta ){\text{sin}}^2(\theta /2)\right)}^{1/2}}-\frac{1}{{\left(1+4\beta (1+\beta ){\text{sin}}^2({\theta }_0/2)\right)}^{1/2}}\right\}\end{array}}$

Cuando el péndulo alcanza la desviación máxima θ =θ₀ partiendo de la posición de equilibrio θ =0, ha empleado un tiempo igual a un cuarto de periodo. El periodo es

${\displaystyle P=4\sqrt{\frac{\beta l}{2g}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{\sqrt{\frac{1}{\sqrt{1+\gamma {\text{sin}}^{\text{2}}(\theta /2)}}-\frac{1}{\sqrt{1+\gamma {\text{sin}}^{\text{2}}({\theta }_0/2)}}}}}}$

donde γ=4β(1+β)

Si θ₀/2 es pequeño, se puede hacer la siguiente aproximación (1+x)^-1/2≈1-x/2

${\displaystyle \frac{1}{\sqrt{1+\gamma {\text{sin}}^2(\theta /2)}}-\frac{1}{\sqrt{1+\gamma {\text{sin}}^2({\theta }_0/2)}}\approx \frac{\gamma }{2}\left({\text{sin}}^2({\theta }_0/2)-{\text{sin}}^2(\theta /2)\right)}$

El periodo P es aproximadamente

${\displaystyle P=4\sqrt{\frac{l}{g}}\sqrt{\frac{1}{(1+\beta )}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d(\theta /2)}{\sqrt{{\text{sin}}^{\text{2}}({\theta }_0/2)-{\text{sin}}^{\text{2}}(\theta /2)}}}}$

Esta integral elíptica ha aparecido al calcular el periodo de un péndulo. Sustituyendo

${\displaystyle \text{sin}\phi =\frac{\text{sin}\frac{\theta }{2}}{\text{sin}\frac{{\theta }_0}{2}}k=\text{sin}\frac{{\theta }_0}{2}}$

Cuando el péndulo alcanza la desviación máxima θ=θ₀, la variable φ=π/2

${\displaystyle P=4\sqrt{\frac{l}{g}}\sqrt{\frac{1}{(1+\beta )}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}=\frac{2P_0}{\pi }\sqrt{\frac{1}{(1+\beta )}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}}$

donde P₀ es el periodo de un péndulo simple de longitud l.

Las integrales elípticas están tabuladas, véase Puig Adam, Calculo Integral. Editorial Biblioteca Matemática 1972,  pág 97.

Si comparamos esta fórmula con la del periodo de un péndulo para cualquier amplitud, observamos que el efecto de la esfericidad de la Tierra es la de reducir el periodo proporcionalmente al factor raíz cuadrada de 1/(1+β).

Ejemplo: Sea β=l/R=0.5, la desviación inicial del péndulo θ₀=10º

• La longitud el péndulo es l=3.185·10⁶ m

• La aceleración de la gravedad en la superficie de la Tierra es g=9.83m/s²

• El periodo del péndulo simple, suponiendo que la aceleración de la gravedad es constante en módulo y dirección

${\displaystyle P_0=2\pi \sqrt{\frac{l}{g}}=2\pi \sqrt{\frac{3.185·{10}^6}{9.83}}=3576.5\text{s}}$

Este script calcula la integral elíptica

${\displaystyle \frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}k=\sin \frac{{\theta }_0}{2}}$

>> angulo=10;
>> ellipke(sin(angulo*pi/(2*180))^2)*2/pi
ans =    1.0019

Como el efecto de la esfericidad de la Tierra es la de reducir el  periodo de este péndulo proporcionalmente al factor raíz cuadrada de 1/(1+β). El periodo del péndulo es

La resolución de la ecuación diferencial por procedimientos numéricos nos proporciona el valor P=49.33 min

Actividades

Se introduce

• El parámetro β=l/R, cociente entre la longitud del péndulo y el radio de la Tierra R=6.37·10⁶ m, actuando en el control titulado Longitud/r. Tierra

• El ángulo θ₀, desviación inicial del péndulo respecto de la línea que une el centro de la Tierra y el punto de suspensión del péndulo, en el control titulado Ángulo

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del péndulo. Una flecha indica la magnitud y dirección de la componente tangencial de la fuerza de atracción entre la Tierra y la masa puntual.

En la parte superior, se proporcionan los datos:

• El tiempo t en minutos.
• El ángulo θ que forma el péndulo con la línea que une el centro de la Tierra y el punto de suspensión del péndulo.
• La velocidad de la masa puntual l·dθ/dt.

Referencias

Burko L. M. Effect of the spherical Earth on a simple pendulum. Eur. J. Phys. 24 (2003), pp. 125-130