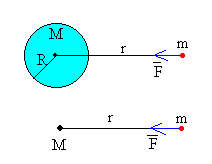
La masa de la Tierra se puede determinar una vez que se conoce el valor de la constante G.

En primer lugar, la fuerza de atracción de una distribución esférica de masa de radio R y masa M sobre una partícula de masa m situada fuera de la esfera, es equivalente al de una partícula cuya masa sea la de la esfera situada en su centro.

Aplicamos la segunda ley de Newton a un cuerpo de masa m que cae libremente, sabiendo que su aceleración de caída, en las proximidades de la superficie de la Tierra es g.

${\displaystyle G\frac{Mm}{R^2}=mgM=\frac{R^{2}g}{G}}$

Como el radio R de la Tierra es conocido y g también puede ser medido mediante varias experiencias, una de las más simples es la medida del tiempo t que tarda en caer un cuerpo una determinada altura h, h=gt²/2.

Si la aceleración de la gravedad medida es g=9.8 m/s² y el radio de la Tierra, supuesta esférica es R =6.37·10⁶ m tenemos que la masa de la Tierra es

${\displaystyle M=\frac{9.8·{(6.37·{10}^6)}^2}{6.67·{10}^{-11}}=5.96·{10}^{24}\text{kg}}$

Calculamos la densidad media de la Tierra dividiendo la masa M entre el volumen de una esfera de radio R, resultando ρ=5506.5 kg/m³=5.5 g/cm³.

Medida de la constante G

El objetivo de la experiencia de Cavendish no era la medida de la constante G, sino la medida de la densidad media de la Tierra. En este apartado, se simula una experiencia de laboratorio para la medida de la constante G

La balanza de gravitación es un instrumento muy sensible que permite demostrar la atracción entre dos masas y determinar el valor de la constante G.

A la izquierda, fotografía de la balanza del laboratorio de la Escuela de Ingeniería de Eibar

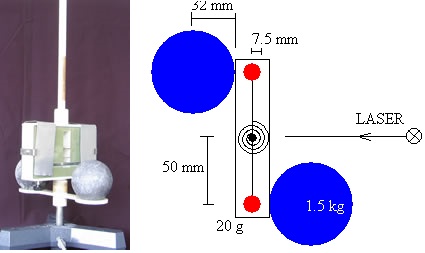
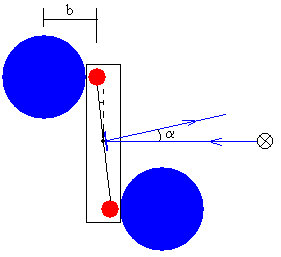
El péndulo de torsión consta de un hilo de torsión cuya constante K es del orden 10^-8 N·m. Por su extremo inferior sujeta a una varilla horizontal de masa despreciable que tiene dos pequeñas esferas de m=20 g de masa cada una y de 7.5 mm de radio. La distancia del hilo de torsión al centro de cada una de las esferas es d=50 mm.

El péndulo oscila con un periodo de aproximadamente, 10 minutos.

Estas pequeñas esferas son atraídas por dos esferas fijas de M=1.5 kg de masa y de 32 mm de radio.

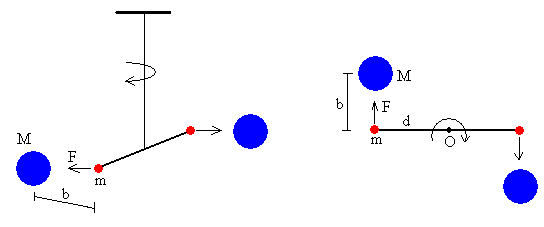
Para determinar la constante G, mediante la balanza de gravitación es necesario medir la posición inicial y la final de equilibrio y el movimiento oscilatorio amortiguado entre estas dos posiciones. El ángulo entre estas posiciones de equilibrio es una medida de la fuerza de atracción. Para medir el ángulo, se dispone de un haz LASER que incide sobre un espejo cóncavo. La oscilación del péndulo, se observa indirectamente mediante el movimiento de la marca luminosa producida por el rayo reflejado en una regla graduada situada a L=4.425 m de distancia.

Posición inicial de equilibrio

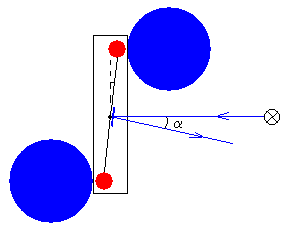
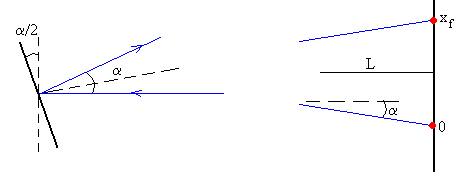
En la posición inicial de equilibrio, debido a la fuerza de atracción de las dos esferas grandes sobre las pequeñas, el péndulo gira un ángulo –α/2. El ángulo que forma el rayo incidente y reflejado es α. La regla marca la posición x₀=0.

Oscilaciones del péndulo

Una vez que el péndulo se mantiene estable en la posición inicial de equilibrio, las esferas grandes se mueven rápidamente a la posición diametralmente opuesta. El péndulo empieza a oscilar con un periodo

${\displaystyle P=2\pi \sqrt{\frac{2m{d}^2}{K}}K=\frac{8{\pi }^{2}m{d}^2}{P^2}}$

donde 2md² es el momento de inercia de la varilla de masas despreciable y de las dos esferas consideradas como masas puntuales, y K es la constante de torsión del hilo.

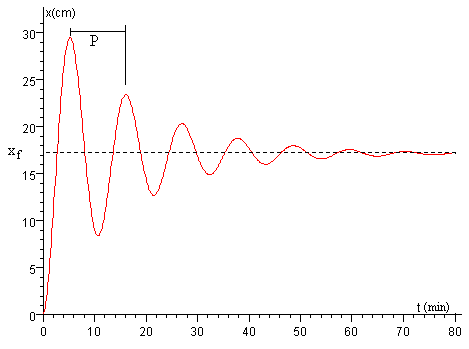
Se mide el periodo P de las oscilaciones tal como se muestra en la figura, el tiempo que trascurre entre dos máximos de la amplitud.

La constante de amortiguamiento es pequeña, de modo que el péndulo oscila durante bastante tiempo antes de alcanzar la posición final de equilibrio

Posición final de equilibrio

La fuerza de atracción entre la esfera grande y la pequeña es

${\displaystyle F=G\frac{Mm}{b^2}}$

El momento del par de fuerzas debido a la atracción entre las esferas, respecto del eje de oscilación, hace que el péndulo gire un ángulo α/2. El ángulo que forma el rayo incidente y reflejado es α. La regla marca la posición x_f.

${\displaystyle 2Fd=K\frac{\alpha }{2}}$

La posición x_f de la marca luminosa sobre la regla distante L del espejo cóncavo es

${\displaystyle \tan \alpha \approx \alpha =\frac{x_f}{2L}}$

ya que α es un ángulo pequeño

${\displaystyle G\frac{Mm}{b^2}=\frac{K\alpha }{4d}=\frac{1}{4d}\frac{8{\pi }^{2}m{d}^2}{P^2}\frac{x_f}{2L}}$

Despejamos la constante G

${\displaystyle G=\frac{{\pi }^2{b}^{2}d}{M{P}^{2}L}{x}_f}$

Ejemplo:

• El periodo del péndulo es el intervalo de tiempo entre dos máximos, en la gráfica x-t de la oscilación, P=10.8 min=648 s

• Posición final de equilibrio en la regla, x_f=17.3 cm

• Distancia del espejo de la balanza de torsión a la regla, L=4.425 m

• Masa de la esfera grande, M=1.5 kg

• Distancia entre los centros de la esfera grande y de la esfera peqeña en la posición de equilibrio es b=0.047 m

• Distancia de la pequeña esfera al eje de oscilación d=0.05 m

${\displaystyle G=\frac{{\pi }^2{0.047}^2·0.05}{1.5·{648}^2·4.425}0.173=6.77·{10}^{-11}{\text{Nm}}^{\text{2}}{\text{/kg}}^{\text{2}}}$

Actividades

El programa interactivo, genera aleatoriamente, un valor de la constante K de torsión dentro de ciertos límites.

Se pulsa el botón titulado Nuevo

El péndulo de torsión se sitúa en la posición inicial de equilibrio

Se pulsa el botón   ►  .

Las esferas grandes se sitúan en posición diametralmente opuesta. El péndulo de torsión comienza a oscilar, hasta que al cabo de un cierto tiempo medido en minutos, se para en la posición final de equilibrio.

Se mide el periodo P de la oscilación, utilizando el botón >| y la posición x_f final de equilibrio. Se calcula la constante G de la ley de la Gravitación Universal.

Referencias

Instrucciones de servicio. Balanza de gravitación, 332 101, Leybold Didactic GMBH