Preparación de los datos

Visitamos la página web, titulada 'Data Services Products: EMC-PREM Preliminary Reference Earth Model'. Descargamos el fichero PREM500_IDV.csv, o alternativamente, en este enlace

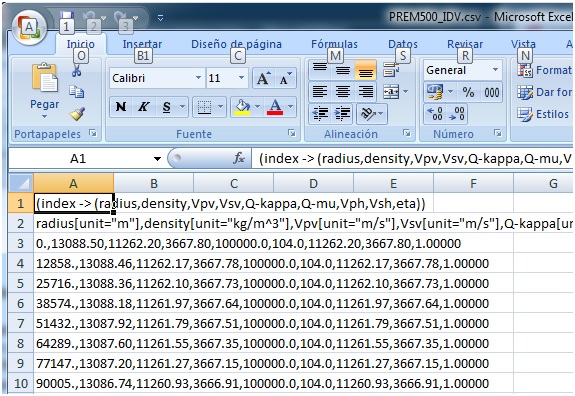
que como apreciamos en la cabecera (primera y segunda fila) contiene los datos del radio en metros (primera columna) y de la densidad en kg/m³ (segunda columna). Las otras columnas de datos no tienen interés. En total 504 filas de pares de datos (radio, densidad). La densidad de la Tierra es esféricamente simétrica, depende solamente de la distancia (radio) del punto considerado al centro de la Tierra

Situamos el fichero, en la carpeta accesible por MATLAB por defecto, e importamos, utilizando en el menú Import data from file, las dos primeras columnas, poniendo en el control titulado Range A3:B506. Pulsamos el botón titulado Import Selection, eligiendo la opción Import Data.

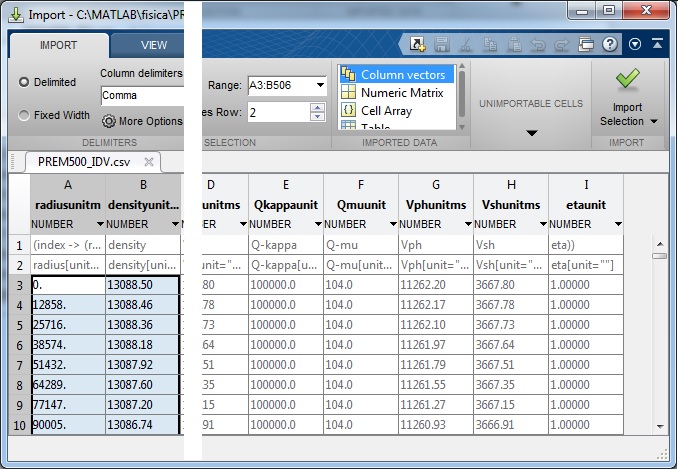
MATLAB genera dos vectores con nombres por defecto que aparecen en la ventana Wokspace.

Si hemos importado todas las columnas, podemos borrar las no deseadas utilizando el botón derecho del ratón y seleccionado en el menú flotante Delete (Suprimir). En esta ocasión, preferimos operar con números más pequeños, creamos dos nuevos vectores densidad y radio

>> densidad=density/1000;
>> radio=indexradius/1e6;

y borramos de Workspace los vectores density e indexradius

Tenemos dos vectores de 504 elementos de longitud cada uno. El primer elemento del vector radio(1) es cero y el último es el radio de la Tierra, radio(end)*1000, en km

>> length(radio)
ans =   504
>> radio(1)
ans =     0
>> radio(end)*1000
ans =        6371

Aceleración de la gravedad

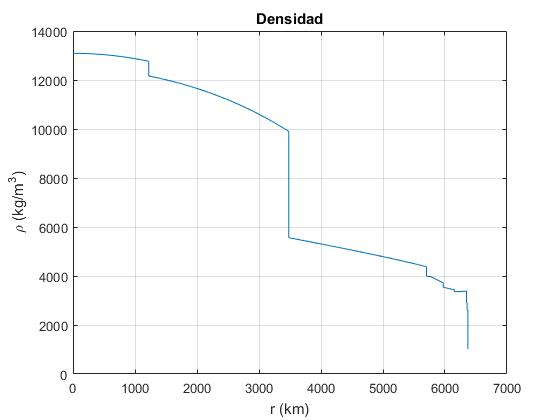
Representamos la densidad en kg/m³ en el eje vertical en función del radio en km en el eje horizontal

plot(radio*1000,densidad*1000)
grid on
xlabel('r (km)')
ylabel('\rho (kg/m^3)')
title('Densidad')

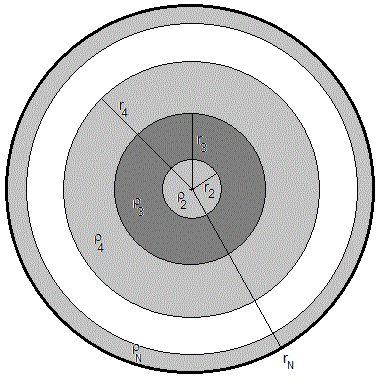
Se ha dividido la Tierra en 503 capas: la primera es una esfera de radio r₂ de densidad ρ₂, la segunda capa esférica de radio interior r₂ y radio exterior r₃ de densidad ρ₃, la tercera capa esférica de radio interior r₃ y radio exterior r₄ de densidad ρ₄...la última capa esférica de radio interior r₅₀₃ y radio exterior r₅₀₄ (radio de la Tierra) de densidad ρ₅₀₄

La masa de la Tierra es

${\displaystyle M=\frac{4}{3}\pi {\displaystyle \sum _{j=2}^N{\rho }_j\left(r_j^3-r_{j-1}^3\right)}}$

Como el radio se ha dividido entre 10⁶ y la densidad entre 10³, el factor de conversión de unidades es 10³(10⁶)³=10²¹, para obtener la masa de la Tierra en kg

masa=0;
for i=2:length(radio)
  masa=masa+densidad(i)*4*pi*(radio(i)^3-radio(i-1)^3)/3;  
end
display(masa*1e21)

   5.9687e+24

La masa M_i contenida en la esfera de radio r_i es

${\displaystyle M(r_i)=\frac{4}{3}\pi {\displaystyle \sum _{j=2}^i{\rho }_j\left(r_j^3-r_{j-1}^3\right)}}$

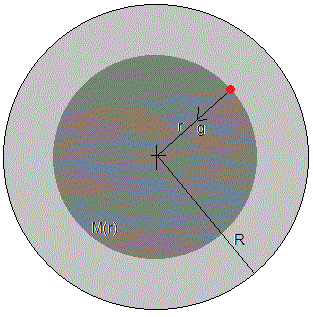
La aceleración de la gravedad en el interior de una distribución esférica de masa de radio R, es la fuerza con la que la masa M(r) contenida en la esfera de radio r<R, atrae a la unidad de masa situada a una distancia r del centro, tal como se muestra en la figura. La aceleración de la gravedad tiene dirección radial y apunta hacia el centro (no tendremos en cuenta el movimiento de rotación de la Tierra)

${\displaystyle g(r)=G\frac{M(r)}{r^2}}$

Creamos una nueva tabla de datos (radio r_i, aceleración de la gravedad g_i). Representamos esta tabla del misma forma que se ha hecho con la densidad.

${\displaystyle g(r_i)=G\frac{M(r_i)}{r_i^2}}$

La aceleración de la gravedad en el exterior de la Tierra, disminuye con el cuadrado de la distancia al centro, siendo M(R) la masa de la Tierra

${\displaystyle g(r)=G\frac{M(R)}{r^2},r>R}$

El factor de conversión de unidades es 6.67·10^-11·10²¹/(10⁶)²=6.67·10^-2

%aceleración de la gravedad en el interior
masa=0;
g=zeros(1,length(radio));
for i=2:length(radio)
  masa=masa+densidad(i)*4*pi*(radio(i)^3-radio(i-1)^3)/3;  
  g(i)=masa*6.67e-2/radio(i)^2;
end
hold on
plot(radio*1000,g)
line([0,radio(end)*1000],[g(end), g(end)],'lineStyle','--','color','k')

%aceleración de la gravedad en el exterior de la Tierra
f=@(x) 6.67e4*masa./(x.^2);  %x en km, 10^-11*10^21/(10^3)^2=10^4
fplot(f,[radio(end)*1000,9000])
line([radio(end)*1000,radio(end)*1000],[0,f(radio(end)*1000)],
'lineStyle','--','color','k')
hold off

grid on
xlabel('r (km)')
ylabel('g (m/s^2)')
title('Aceleración de la gravedad')

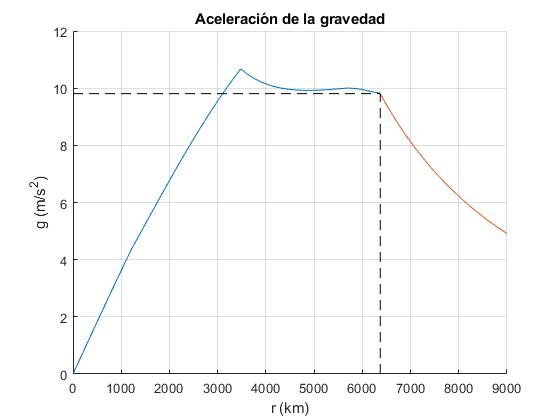
La aceleración de la gravedad en la superficie de la Tierra es

>> g(end)
ans =    9.8083

Siguiendo el modelo de capas, dado el radio r<R, calculamos la masa M(r) contenida en dicha esfera. Supongamos que r_i<r<r_i+1

${\displaystyle M(r)=\frac{4}{3}\pi {\displaystyle \sum _{j=2}^i{\rho }_j\left(r_j^3-r_{j-1}^3\right)}+\frac{4}{3}\pi {\rho }_{i+1}\left(r^3-r_i^3\right)}$

Definimos una función que devuelve la aceleración de la gravedad g(r) para cualquier valor de r<R

function g = gravedad_interior(r, radio,densidad)
    masa=0;    
    if r>radio(2)
        indice=find(radio<r);
        i=indice(end);
        for j=2:i
            masa=masa+densidad(j)*4*pi*(radio(j)^3-radio(j-1)^3)/3;  
        end
        masa=masa+densidad(i+1)*4*pi*(r^3-radio(i)^3)/3;
    end
    g=6.67e-2*masa/r^2;
end

Utilizamos esta función para representar, alternativamente, la aceleración de la gravedad en el interior de la Tierra

r=linspace(0,radio(length(radio)),300);
g=zeros(1,length(r));
for j=1:length(r)
    g(j)=gravedad_interior(r(j), radio,densidad);
end
plot(r*1000,g)
grid on
xlabel('r (km)')
ylabel('g (m/s^2)')
title('Aceleración de la gravedad')

Túnel a través de un diámetro

La fuerza que ejerce el campo gravitatorio producido por la Tierra sobre una partícula de masa m es el producto de su masa por la aceleración de la gravedad g(r). La aceleración de la gravedad en el interior de la Tierra es M(r)/r² y en el exterior es M/r², siendo M la masa de la Tierra.

El nivel cero de energía potencial se encuentra en el infinito, de modo que la energía potencial de una partícula de masa m situada a una distancia r del centro de la Tierra es

${\displaystyle E_p(r)={\displaystyle \underset{r}{\overset{R}{\int }}-G\frac{M(r)m}{r^2}dr}+{\displaystyle \underset{R}{\overset{\infty }{\int }}-G\frac{M·m}{r^2}dr}=-{\displaystyle \underset{r}{\overset{R}{\int }}G\frac{M(r)m}{r^2}dr}-G\frac{Mm}{R}}$

Velocidad

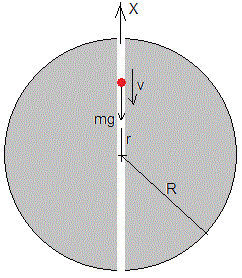
Supongamos que excavamos un túnel a través de un diámetro de la Tierra. Soltamos la partícula en el extremo del túnel, en la superficie de la Tierra, su velocidad cuando está a una distancia r del centro se calcula aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+E_p(r)=E_p(R)\\ v^2=2{\displaystyle \underset{r}{\overset{R}{\int }}G\frac{M(r)}{r^2}dr}=2{\displaystyle \underset{r}{\overset{R}{\int }}g(r)dr}\end{array}}$

Calculamos la velocidad v en función en función de la distancia de la partícula al centro de la Tierra r. Utilizamos la función gravedad_interior y el procedimiento de Simpson, para calcular la integral definida entre r y R

function suma=simpson(f,x0,xf,n)
%n número par de intervalos, n+1 número de puntos en el vector    
    x=linspace(x0,xf,n+1);   
    h=x(2)-x(1);
    suma=f(x(1))+f(x(n+1));
    for i=2:2:n
        suma=suma+4*f(x(i));
    end
    for i=3:2:n-1
        suma=suma+2*f(x(i));
    end
    suma=suma*h/3;
end

Como el radio r está dividido entre 10⁶, hay que multiplicar el resultado de la integral por 10⁶, es decir, la velocidad por 1000

r=linspace(0,radio(end),300);
f=@(r) gravedad_interior(r,radio, densidad); 
v=zeros(1,length(r));
for i=2:length(r)
    v(i)=sqrt(2*simpson(f,r(i),radio(end),100));
end
plot(r(2:end)*1000,v(2:end)*1000)
grid on
xlabel('r (km)')
ylabel('v (m/s)')
title('Velocidad')

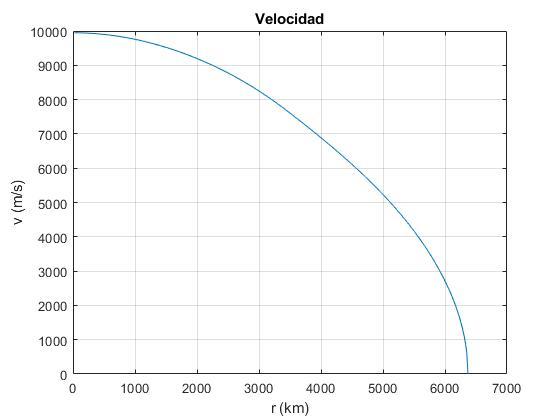
La velocidad cuando llega al centro de la Tierra es

>> v(2)*1000
ans =   9.9127e+03

Ecuación del movimiento

Situamos el origen en el centro de la Tierra y el eje X tal como se muestra en la figura. Cuando la partícula se encuentra a una distancia x del centro, la fuerza que actúa sobre la partícula es mg(x). La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-mg(x)}$

Se resuelve la ecuación diferencial por el procedimiento ode45 de MATLAB con las condiciones iniciales siguientes: en el instante t=0, x=R y dx/dt=0, parte del reposo desde el extremo del túnel en la superficie de la Tierra.

Primero, definimos la función a integrar, que calcule la aceleración de la gravedad para una distancia r al centro de la Tierra, tarea que hemos realizado en la función gravedad_interior

function fg=gravedad_variable(~,x, radio,densidad)    
    masa=0; 
    r=x(1);
    if r>radio(2)
        indice=find(radio<r);
        i=indice(end);
        for j=2:i
            masa=masa+densidad(j)*4*pi*(radio(j)^3-radio(j-1)^3)/3;  
        end
        masa=masa+densidad(i+1)*4*pi*(r^3-radio(i)^3)/3;
    end
    fg=[x(2);-6.67e-2*masa/x(1)^2];
end

En segundo lugar, definimos una función para que el procedimiento ode45 se detenga cuando la partícula llegue al centro de la Tierra x=0

function [value,isterminal,direction]=stop_gravedad(t,x)
    value=x(1); 
   isterminal=1;
    direction=-1; 
end

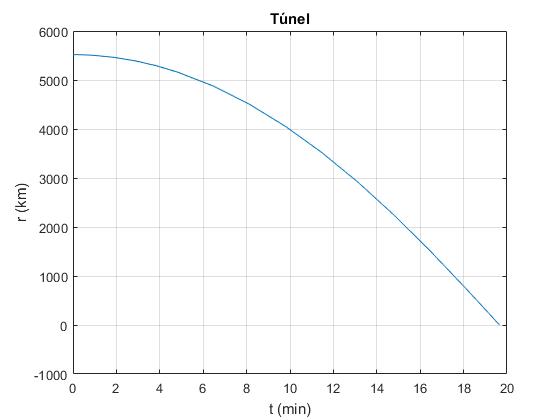
Creamos el script para calcular y representar la posición x de la partícula en el túnel en función del tiempo t

ffg=@(t,x) gravedad_variable(t,x,radio, densidad); 
opts=odeset('events',@stop_gravedad);
[t,x, te]=ode45(fg,[0,4],[radio(end),0], opts);
plot(t*1000/60,x(:,1)*1000)
grid on
xlabel('t (min)')
ylabel('r (km)');
title('Túnel')

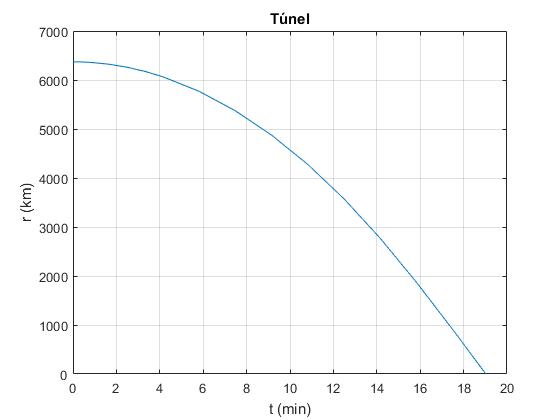
El tiempo que tarda en llegar al centro de la Tierra en minutos y su velocidad son, respectivamente

>> te*1000/60
ans =   19.0930
>> x(end,2)*1000
ans =  -9.9515e+03

El perido de una oscilación es cuatro veces este tiempo, 76.4 min

Túnel a través de una cuerda

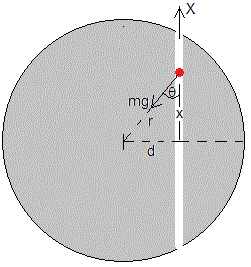
Cuando la partícula se mueve por un túnel excavado a lo largo de una cuerda distante d del centro, la componente de la fuerza sobre la partícula a lo largo del eje X es

${\displaystyle mg(r)\cos \theta =mg(r)\frac{x}{r}}$

La ecuación del movimiento se escribe

${\displaystyle \frac{d^{2}x}{d{t}^2}=-g(r)\frac{x}{r}}$

Se resuelve la ecuación diferencial por el procedimiento ode45 de MATLAB con las condiciones iniciales siguientes: en el instante t=0, $x_0=\sqrt{R^2-d^2}$ y dx/dt=0, parte del reposo desde el extremo del túnel en la superficie de la Tierra

Primero, definimos la función a integrar, que calcule la aceleración de la gravedad para una distancia r al centro de la Tierra, tarea que hemos realizado al definir las funciones gravedad_interior y gravedad_variable

function fg=gravedad_variable_1(~,x, radio,densidad, d)    
    r=sqrt(x(1)^2+d^2);
    masa=0;  
    if r>radio(end)
       r=radio(end);
    end
    if r>radio(2)
        indice=find(radio<r);
        i=indice(end);
        for j=2:i
            masa=masa+densidad(j)*4*pi*(radio(j)^3-radio(j-1)^3)/3;  
        end
        masa=masa+densidad(i+1)*4*pi*(r^3-radio(i)^3)/3;
    end
    fg=[x(2);-6.67e-2*masa*x(1)/r^3];
end

En segundo lugar, utilizamos la función stop_gravedad definida en el apartado anterior, para que el procedimiento ode45 se detenga cuando la partícula llegue al centro del túnel x=0

Creamos el script para calcular y representar la posición x de la partícula en el túnel en función del tiempo t. El túnel dista R/2 del centro de la Tierra

d=0.5*radio(end);
fg=@(t,x) gravedad_variable_1(t,x,radio, densidad, d); 
opts=odeset('events',@stop_gravedad);
[t,x, te]=ode45(fg,[0,4],[sqrt(radio(end)^2-d^2),0], opts);
plot(t*1000/60,x(:,1)*1000)
grid on
xlabel('t (min)')
ylabel('r (km)');
title('Túnel')

El tiempo que tarda en llegar al centro del túnel en minutos y su velocidad son, respectivamente

>> te*1000/60, x(end,2)*1000
ans =   19.7047
ans =  -8.0039e+03

Modificamos el script para calcular el tiempo de llegada de la partícula al centro del túnel para distintas distancias d del túnel al centro de la Tierra

opts=odeset('events',@stop_gravedad);
j=1;
distancias=0:0.05:0.95;
T=zeros(1,length(distancias));
for d=distancias*radio(end)
    fg=@(t,x) gravedad_variable_1(t,x,radio, densidad, d); 
    [t,x, te]=ode45(fg,[0,4],[sqrt(radio(end)^2-d^2),0], opts);
    T(j)=te;
    j=j+1;
end
plot(distancias*radio(end)*1000,T*1000/60,'-o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
grid on
xlabel('r (km)')
ylabel('T (min)');
title('Túnel')

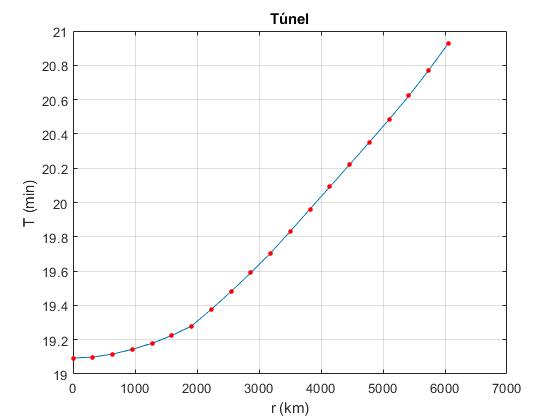
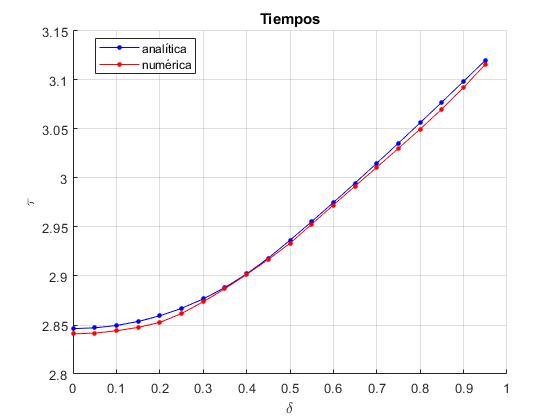
En el modelo de densidad constante del interior de la Tierra todos los tiempos eran iguales, en el modelo PREM los tiempos son diferentes, siendo mínimo cuando el túnel está excavado a través de un diámetro

Aceleración de la gravedad. Ajuste

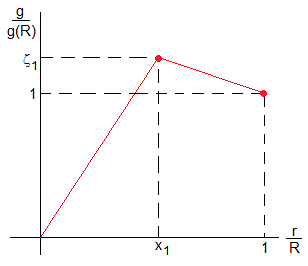
La forma de la curva de la acelaración de la gravedad en función de la distancia al centro de la Tierra, nos sugiere la posibilidad de dividirla en dos capas, en la primera la aceleración de la gravedad crece linealmente con el radio y en la segunda, la aceleración de la gravedad disminuye linealmente con el radio. Las ecuaciones de las rectas que se ha dibujado en color rojo en la figura son

${\displaystyle \zeta (x)=\{\begin{array}{l}\frac{{\zeta }_1}{x_1}x0\le x\le x_1\\ \frac{1-{\zeta }_1}{1-x_1}x+\frac{{\zeta }_1-x_1}{1-x_1}{x}_1\le x\le 1\end{array}}$

Buscamos los valores de los parámetros x₁ y ζ₁ que hacen que la función ζ(x) se ajuste a los valores calculados de la aceración de la gravedad g(r)/g(R) en función de x=r/R. g(R) es la aceleración de la gravedad en la superficie de la Tierra. Véase la página titulada Ajuste de datos (no lineal), la sección 'Ajuste mediante nlinfit o fminsearch'

masa=0;
g=zeros(1,length(radio));
for i=2:length(radio)
  masa=masa+densidad(i)*4*pi*(radio(i)^3-radio(i-1)^3)/3;  
  g(i)=masa*6.67e-2/radio(i)^2;
end
hold 
x=radio'/radio(end); %vector fila
y=g/g(end); %vector fila
plot(x,y)

%ajuste
f=@(a,x) a(1)*(x<a(2)).*x/a(2)+(x>=a(2)).*(((1-a(1))*x+a(1)-a(2))/(1-a(2)));
error=@(a) sum((y-f(a,x)).^2);
a0=[1,0.5];  %valor inicial
af=fminsearch(error,a0);
g=@(x) f(af,x);
fplot(g,[0,1])
line([af(2),af(2)],[0,af(1)],'lineStyle','--', 'color','k')
hold off

grid on
xlabel('r/R')
ylabel('g/g(R)')
title('Aceleración de la gravedad')

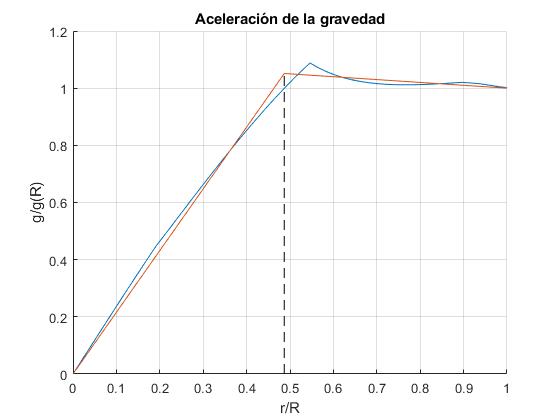
Los valores de los parámetros ζ₁ y x₁ son

>> af
af =    1.0514    0.4869

Túnel a través de una cuerda

Velocidades

Calculamos la velocidad adimensional $\vartheta (x)$

${\displaystyle \begin{array}{l}{v}^2(r)=2{\displaystyle \underset{r}{\overset{R}{\int }}g(r)dr}\\ v^2(r)=2g(R){\displaystyle \underset{r}{\overset{R}{\int }}\frac{g(r)}{g(R)}dr}\\ {\vartheta }^2(x)={\left(\frac{v(r)}{R·g(R)}\right)}^2=2{\displaystyle \underset{x}{\overset{1}{\int }}\zeta (x\text{'})dx\text{'}}\end{array}}$

Hay dos posibilidades

• Para x₁≤x≤1

${\displaystyle \begin{array}{l}{\vartheta }_1^2(x)=2{\displaystyle \underset{x}{\overset{1}{\int }}\left(\frac{1-{\zeta }_1}{1-x_1}x\text{'}+\frac{{\zeta }_1-x_1}{1-x_1}\right)dx}\text{'}\\ {\vartheta }_1^2(x)=(1-x)\left(-\frac{{\zeta }_1-1}{1-x_1}x+\frac{{\zeta }_1-2x_1+1}{1-x_1}\right)\\ {\vartheta }_1(x)=\sqrt{(1-x)\left(-\mu x+\mu +2\right)},\mu =\frac{{\zeta }_1-1}{1-x_1},x_1\le x\le 1\end{array}}$

• Para 0≤x≤x₁

${\displaystyle \begin{array}{l}{\vartheta }_2^2(x)=2{\displaystyle \underset{x}{\overset{x_1}{\int }}\frac{{\zeta }_1}{x_1}x\text{'}·dx}\text{'}+2{\displaystyle \underset{x_1}{\overset{1}{\int }}\left(\frac{1-{\zeta }_1}{1-x_1}x+\frac{{\zeta }_1-x_1}{1-x_1}\right)dx}\\ {\vartheta }_2(x)=\sqrt{1+{\zeta }_1-x_1-\frac{{\zeta }_1}{x_1}{x}^2}0\le x\le x_1\end{array}}$

Vamos a buscar, soluciones analíticas para calcular el tiempo que tarda una partícula en recorrer un túnel que atraviesa la Tierra

Primer caso, δ>x₁

La partícula se deja caer en el extremo del túnel. El tiempo T que tarda en recorrer el túnel es

${\displaystyle T=2{\displaystyle \underset{\sqrt{R^2-d^2}}{\overset{0}{\int }}\frac{dy}{v(y)}}}$

Cambiamos la variable y por la variable r,

${\displaystyle \begin{array}{l}{r}^2=d^2+y^2\\ 2rdr=2ydy\\ T=2{\displaystyle \underset{R}{\overset{d}{\int }}\frac{rdr}{v(r)\sqrt{r^2-d^2}}}\\ T=\frac{2R}{\sqrt{R·g(R)}}{\displaystyle \underset{1}{\overset{\delta }{\int }}\frac{xdx}{\vartheta (x)\sqrt{x^2-{\delta }^2}}}\end{array}}$

Introducimos la expresión de la velocidad adimensional ${\vartheta }_1(x)$, válida en el intervalo x₁≤x≤1

${\displaystyle \begin{array}{l}T=2\sqrt{\frac{R}{g(R)}}{\displaystyle \underset{1}{\overset{\delta }{\int }}\frac{xdx}{\sqrt{(x-\delta )(x+\delta )(1-x)\left(\mu +2-\mu x\right)}}}\\ T=2\sqrt{\frac{R}{g(R)}}\frac{1}{\sqrt{\mu }}{\displaystyle \underset{1}{\overset{\delta }{\int }}\frac{xdx}{\sqrt{\left(\frac{\mu +2}{\mu }-x\right)(1-x)(x-\delta )(x+\delta )}}}\end{array}}$

En el libro titulado 'Table of Integrals, Series, and Products' buscamos la solución a integrales de este tipo y la encontramos en el apartado 3.148, n° 5 de la página 276

${\displaystyle \begin{array}{l}{\displaystyle \underset{b}{\overset{u}{\int }}\frac{x·dx}{\sqrt{(a-x)(b-x)(x-c)(x-d)}}}=\frac{2}{\sqrt{(a-c)(b-d)}}\left\{(b-a)\Pi \left(\kappa ,\frac{b-c}{a-c},q\right)+aF(\kappa ,q)\right\}\\ \kappa =\arcsin \sqrt{\frac{(a-c)(b-u)}{(b-c)(a-u)}},q=\sqrt{\frac{(b-c)(a-d)}{(a-c)(b-d)}}\end{array}}$

Identificamos las variables

${\displaystyle \begin{array}{l}a=\frac{\mu +2}{\mu },b=\mathrm{1,}c=\delta ,d=-\delta ,u=\delta \\ a\ge b>u\ge c>d\\ \kappa =\arcsin \sqrt{\frac{(a-c)(b-u)}{(b-c)(a-u)}}=\arcsin (1),\kappa =\frac{\pi }{2}\\ q=\sqrt{\frac{(1-\delta )\left(\frac{\mu +2}{\mu }+\delta \right)}{\left(\frac{\mu +2}{\mu }-\delta \right)(1+\delta )}=}\sqrt{\frac{(1-\delta )\left(\mu +2+\delta \mu \right)}{\left(\mu +2-\mu \delta \right)(1+\delta )}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}T=4\sqrt{\frac{R}{g(R)}}\frac{1}{\sqrt{\mu }}{\displaystyle \underset{1}{\overset{\delta }{\int }}\frac{xdx}{\sqrt{\left(\frac{\mu +2}{\mu }-x\right)(1-x)(x-\delta )(x+\delta )}}}=\\ =\sqrt{\frac{R}{g(R)}}·\frac{4}{\sqrt{\left(\mu +2-\delta \mu \right)(1+\delta )}}\left\{\left(\frac{\mu +2}{\mu }\right)F\left(\frac{\pi }{2},q\right)-\frac{2}{\mu }·\Pi \left(\frac{\pi }{2},\frac{\mu (1-\delta )}{\mu +2-\delta \mu },q\right)\right\}\end{array}}$

El tiempo T se expresa en términos de las integrales elípticas completas de primera especie y de tercera, F(π/2,q)=K(q),

Segundo caso, δ<x₁

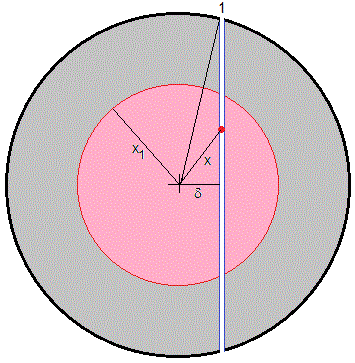
La partícula se deja caer en el extremo del túnel. El tiempo T que tarda en recorrer el túnel es

${\displaystyle T=2{\displaystyle \underset{\sqrt{R^2-d^2}}{\overset{0}{\int }}\frac{dy}{v(y)}}}$

Cambiamos la variable y por la variable r,

${\displaystyle \begin{array}{l}{r}^2=d^2+y^2\\ 2rdr=2ydy\\ T=2{\displaystyle \underset{R}{\overset{d}{\int }}\frac{rdr}{v(r)\sqrt{r^2-d^2}}}\\ T=\frac{2R}{\sqrt{R·g(R)}}{\displaystyle \underset{1}{\overset{\delta }{\int }}\frac{xdx}{\vartheta (x)\sqrt{x^2-{\delta }^2}}}\end{array}}$

Introducimos la expresión de la velocidad adimensional ${\vartheta }_1(x)$, válida en el intervalo x₁≤x≤1 y de ${\vartheta }_2(x)$, válida en el intervalo 0≤x≤x₁

${\displaystyle \begin{array}{l}T=2\sqrt{\frac{R}{g(R)}}\left\{{\displaystyle \underset{1}{\overset{x_1}{\int }}\frac{xdx}{{\vartheta }_1(x)\sqrt{x^2-{\delta }^2}}}+{\displaystyle \underset{x_1}{\overset{\delta }{\int }}\frac{xdx}{{\vartheta }_2(x)\sqrt{x^2-{\delta }^2}}}\right\}\\ T=2\sqrt{\frac{R}{g(R)}}\left\{\frac{1}{\sqrt{\mu }}{\displaystyle \underset{1}{\overset{x_1}{\int }}\frac{xdx}{\sqrt{\left(\frac{\mu +2}{\mu }-x\right)(1-x)(x-\delta )(x+\delta )}}+{\displaystyle \underset{x_1}{\overset{\delta }{\int }}\frac{xdx}{\sqrt{\left(1+{\zeta }_1-x_1-\frac{{\zeta }_1}{x_1}{x}^2\right)\left(x^2-{\delta }^2\right)}}}}\right\}\end{array}}$

La primera integral, es similar al caso anterior. Denominamos

${\displaystyle \begin{array}{l}a=\frac{\mu +2}{\mu },b=\mathrm{1,}c=\delta ,d=-\delta ,u=x_1\\ \kappa =\arcsin \sqrt{\frac{(a-c)(b-u)}{(b-c)(a-u)}}=\arcsin \sqrt{\frac{\left(\frac{\mu +2}{\mu }-\delta \right)(1-x_1)}{(1-\delta )\left(\frac{\mu +2}{\mu }-x_1\right)}}=\arcsin \sqrt{\frac{\left(\mu +2-\mu \delta \right)(1-x_1)}{(1-\delta )\left(\mu +2-\mu x_1\right)}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{1}{\sqrt{\mu }}{\displaystyle \underset{1}{\overset{x_1}{\int }}\frac{xdx}{\sqrt{\left(\frac{\mu +2}{\mu }-x\right)(1-x)(x-\delta )(x+\delta )}}}=\\ \frac{2}{\sqrt{\left(\mu +2-\delta \mu \right)(1+\delta )}}\left\{\left(\frac{\mu +2}{\mu }\right)F\left(\kappa ,q\right)-\frac{2}{\mu }·\Pi \left(\kappa ,\frac{\mu (1-\delta )}{\mu +2-\delta \mu },q\right)\right\}\end{array}}$

La segunda integral se resuelve haciendo el cambio u=x², es similar a la trayectoria de un planeta.

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{xdx}{\sqrt{\left(1+{\zeta }_1-x_1-\frac{{\zeta }_1}{x_1}{x}^2\right)\left(x^2-{\delta }^2\right)}}}=\frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{-a{u}^2+bu+c}}}=\frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{a\left\{\frac{c}{a}+\frac{b^2}{4a^2}-{\left(u-\frac{b}{2a}\right)}^2\right\}}}}\\ c=-\left(1+{\zeta }_1-x_1\right){\delta }^2,b=1+{\zeta }_1-x_1+\frac{{\zeta }_1}{x_1}{\delta }^2,a=\frac{{\zeta }_1}{x_1}\end{array}}$

Hacemos un nuevo cambio de variable

${\displaystyle u-\frac{b}{2a}=\sqrt{\frac{c}{a}+\frac{b^2}{4a^2}}\sin \xi }$

Con este cambio la integral es inmediata

${\displaystyle \frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{a\left\{\frac{c}{a}+\frac{b^2}{4a^2}-{\left(u-\frac{b}{2a}\right)}^2\right\}}}}=\frac{1}{2\sqrt{a}}\xi =\frac{1}{2\sqrt{a}}\arcsin \left(\frac{x^2-\frac{b}{2a}}{\sqrt{\frac{c}{a}+\frac{b^2}{4a^2}}}\right)=\frac{1}{2\sqrt{a}}\arcsin \left(\frac{2a{x}^2-b}{\sqrt{4ac+b^2}}\right)}$

Evaluamos el integrando entre x₁ y δ. Denominamos

${\displaystyle \begin{array}{l}c=-\eta {\delta }^2,b=\eta +\frac{{\zeta }_1}{x_1}{\delta }^2,a=\frac{{\zeta }_1}{x_1},\eta =1+{\zeta }_1-x_1\\ \frac{1}{2\sqrt{a}}\arcsin {\left(\frac{2a{x}^2-b}{\sqrt{4ac+b^2}}\right)}_{x_1}^{\delta }=\frac{1}{2}\sqrt{\frac{x_1}{{\zeta }_1}}\left\{\arcsin \left(\frac{\frac{{\zeta }_1}{x_1}{\delta }^2-\eta }{\sqrt{{\left(\frac{{\zeta }_1}{x_1}{\delta }^2-\eta \right)}^2}}\right)-\arcsin \left(\frac{\frac{{\zeta }_1}{x_1}\left(2x_1^2-{\delta }^2\right)-\eta }{\sqrt{{\left(\frac{{\zeta }_1}{x_1}{\delta }^2-\eta \right)}^2}}\right)\right\}=\\ \frac{1}{2}\sqrt{\frac{x_1}{{\zeta }_1}}\left\{\frac{\pi }{2}-\arcsin \left(\frac{{\zeta }_1\left(2x_1^2-{\delta }^2\right)-\eta x_1}{{\zeta }_1{\delta }^2-\eta x_1}\right)\right\}\end{array}}$

El resultado final es

${\displaystyle T=\sqrt{\frac{R}{g(R)}}\left\{\begin{array}{l}\frac{2}{\sqrt{\left(\mu +2-\delta \mu \right)(1+\delta )}}\left\{\left(\frac{\mu +2}{\mu }\right)F\left(\kappa ,q\right)-\frac{2}{\mu }·\Pi \left(\kappa ,\frac{\mu (1-\delta )}{\mu +2-\delta \mu },q\right)\right\}\\ +\sqrt{\frac{x_1}{{\zeta }_1}}\left\{\frac{\pi }{2}-\arcsin \left(\frac{{\zeta }_1\left(2x_1^2-{\delta }^2\right)-\eta x_1}{{\zeta }_1{\delta }^2-\eta x_1}\right)\right\}\end{array}\right\}}$

El segundo término entre corchetes, se puede simplificar aún más, del siguiente modo:

${\displaystyle \begin{array}{l}\theta =\frac{\pi }{2}-\arcsin \left(\frac{{\zeta }_1\left(2x_1^2-{\delta }^2\right)-\eta x_1}{{\zeta }_1{\delta }^2-\eta x_1}\right)=\frac{\pi }{2}-\phi \\ \sin \theta =\cos \phi =\sqrt{1-{\sin }^2\phi }=\sqrt{1-{\left(\frac{{\zeta }_1\left(2x_1^2-{\delta }^2\right)-\eta x_1}{\eta x_1-{\zeta }_1{\delta }^2}\right)}^2}=\frac{2\sqrt{{\zeta }_1{x}_1\left(x_1^2-{\delta }^2\right)\left(\eta -{\zeta }_1{x}_1\right)}}{\left(\eta x_1-{\zeta }_1{\delta }^2\right)}=\\ 2\left(\frac{\sqrt{\frac{{\zeta }_1}{x_1}}\sqrt{x_1^2-{\delta }^2}}{\sqrt{\eta -\frac{{\zeta }_1}{x_1}{\delta }^2}}\right)\sqrt{\frac{\eta -{\zeta }_1{x}_1}{\eta -\frac{{\zeta }_1}{x_1}{\delta }^2}}=2\sin \varphi \cos \varphi =\sin (2\varphi )\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\theta =2\varphi \\ \frac{\pi }{2}-\arcsin \left(\frac{{\zeta }_1\left(2x_1^2-{\delta }^2\right)-\eta x_1}{\eta x_1-{\zeta }_1{\delta }^2}\right)=2\arcsin \left(\frac{\sqrt{\frac{{\zeta }_1}{x_1}}\sqrt{x_1^2-{\delta }^2}}{\sqrt{\eta -\frac{{\zeta }_1}{x_1}{\delta }^2}}\right)\end{array}}$

Resultados

Comparamos los tiempos adimensionales $\tau =T/\sqrt{\frac{R}{g(R)}}$ en recorrer el túnel mediante cálculo numérico y mediante la aproximación analítica que hemos descrito en este apartado

distancias=0:0.05:0.95;
g1=1.0514;
x1=0.4869;
mu=(g1-1)/(1-x1);
T=zeros(1,length(distancias));
j=1;
hold on
for d=distancias
    q=sqrt((1-d)*(mu+2+d*mu)/((mu+2-mu*d)*(1+d)));
    A=1/sqrt((mu+2-mu*d)*(1+d));
    if d>x1
        T(j)=4*A*((mu+2)*ellipke(q^2)/mu-2*ellipticPi(mu*(1-d)/(mu+2-mu*d),q^2)/mu);
    else
        eta=1+g1-x1;
        k=asin(sqrt((mu+2-mu*d)*(1-x1)/((1-d)*(mu+2-mu*x1))));
        T(j)=sqrt(x1/g1)*(pi/2-asin((g1*(2*x1^2-d^2)-eta*x1)/(g1*d^2-eta*x1)))+
4*A*((mu+2)*ellipticF(k,q^2)/mu-2*ellipticPi(mu*(1-d)/(mu+2-mu*d),k,q^2)/mu);
    end
    j=j+1;
end
plot(distancias,T,'-bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')

TT=zeros(1,length(distancias));
opts=odeset('events',@stop_gravedad);
j=1;
for d=distancias*radio(end)
    fg=@(t,x) gravedad_variable_1(t,x,radio, densidad, d); 
    [t,x, te]=ode45(fg,[0,4],[sqrt(radio(end)^2-d^2),0], opts);
    TT(j)=2*te*1000/sqrt(radio(end)*1e6/9.8083);
    j=j+1;
end
plot(distancias,TT,'-ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('\delta')
ylabel('\tau');
legend('analítica','numérica','Location','best')
title('Tiempos')

Referencias

Alexander R. Klotz. The gravity tunnel in a non-uniform Earth. Am. J. Phys. 83(3) march 2015, pp. 231-237

Stefan Isermann. Analytical solution of gravity tunnels through an inhomogeneous Earth. Am. J. Phys. 87(1), January 2019, pp. 10-17

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier, 2007