Sistema formado por una barca y el barquero

Un problema típico de sistema aislado de dos partículas interactuantes es el sistema formado por un barco y su barquero. Si la barca está tocando con el muelle y el barquero está situado en la popa del barco, cuando camina hacia la proa observa que el barco se aleja del muelle.

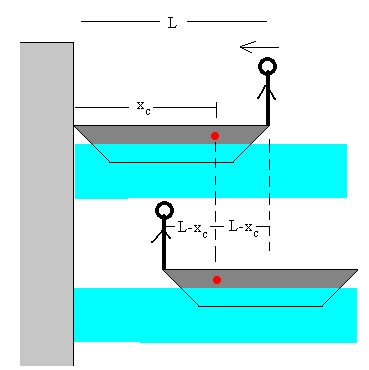
Si la masa del barco es M y la del barquero es m y la longitud del barco es L. La posición del centro de masas del sistema barco-barquero está en x_c medido desde la proa del barco

${\displaystyle x_c=\frac{ML/2+mL}{M+m}}$

La posición x_c está entre el c.m. del barco (en la mitad L/2) y la posición del barquero (L), marcada por un punto rojo en la figura.

Cuando el barquero se mueve hacia la proa, el c.m. del sistema no modifica su posición, ya que se trata de un sistema aislado, cuyo c.m. estaba inicialmente en reposo

Como vemos en la figura inferior, el hombre se ha desplazado hacia la izquierda, 2·(L-x_c)=ML/(m+M) y lo que se ha desplazado el barco respecto del muelle, 2·x_c-L=mL/(m+M).

Supongamos que el barquero se mueve hacia la proa con velocidad constante -v sobre el barco. El barco se moverá hacia la derecha con velocidad constante V, de modo que

${\displaystyle \begin{array}{l}m(-v+V)+MV=0\\ V=\frac{m}{m+M}v\end{array}}$

El barquero tarda un tiempo t=L/v en atravesar el barco, en este tiempo el barco se ha desplazado hacia la derecha V·L/v=mL/(m+M). En este mismo tiempo, el barquero se desplazado

${\displaystyle \left(-v+V\right)\frac{L}{v}=\left(-v+\frac{m}{m+M}v\right)\frac{L}{v}=-\frac{M}{m+M}L}$

Actividades

Se pueden presentar dos casos:

• Cuando el centro de masas está en reposo
• Cuando el centro de masas está en movimiento con velocidad constante

Se introduce

• La masa del barco M en el control titulado Masa barco
• La masa del barquero m en el control titulado Masa barquero.
• El barquero se mueve con velocidad de 50 cm/s respecto del barco, hacia adelante y hacia atrás.

Se puede activar o desactivar la casilla titulada c.m. en movimiento (si queremos que el centro de masas del sistema está en movimiento o en reposo).

Se pulsa el botón Nuevo.

La posición del c.m. del sistema viene señalado por una línea vertical de color azul. Mientras que la posición del c.m. de cada uno de los cuerpos (situada en sus centros) está señalada por una línea vertical de color rojo.

Ejemplo 1:

Introducimos los siguientes datos

• la masa del barco M=200 kg
• la masa del barquero m=80 kg.

La posición del c.m. está en el origen  x_c=0. Si el barquero se desplaza 50 cm hacia la derecha sobre el barco, el barco se deslaza x_b hacia la izquierda. Podemos calcular este desplazamiento a partir de la definición de centro de masa.

${\displaystyle 0=\frac{200·x_b+80(50+x_b)}{200+80}{x}_b=-14.2\text{cm}}$

Si ahora activamos la casilla titulada c.m. en movimiento. Observaremos que la velocidad del c.m. es constante e igual a v_c=25 cm/s. La velocidad del barquero relativa al barco es de 50 cm/s. La velocidad del barco se calcula a partir de la fórmula de la velocidad del c.m.

${\displaystyle 25=\frac{200·v_b+80(50+v_b)}{200+80}{v}_b=10.7\text{cm/s}}$

Ejemplo 2:

Introducimos los siguientes datos

• la masa del barco M=80 kg
• la masa del barquero m=80 kg.

Si ahora activamos la casilla titulada c.m. en movimiento. Observaremos que la velocidad del c.m. es constante e igual a v_c=25 cm/s.

• Cuando el barquero se mueve hacia la derecha, el barco está en reposo v_b=0
• Cuando el barquero se mueve hacia la izquierda, el barco se mueve hacia la derecha con velocidad de v_b=50 cm/s

Una rana salta sobre una tabla

Una tabla de masa M y longitud L flota encima del agua de un estanque, una rana de masa m está situada en uno de los extremos de la tabla, salta con velocidad v₀ relativa a la tabla haciendo un ángulo θ con la horizontal.

Vamos a estudiar el movimiento de la rana sobre la tabla, el movimiento de la tabla y del centro de msas del sistema

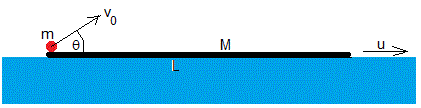
El momento lineal inicial del sistema aislado es cero

Supongamos que la tabla se mueve con velocidad u inmediatamente después de que la rana salte. La velocidad horizontal de la rana respecto al estanque es v₀cosθ+u. El momento lineal del sistema será

${\displaystyle \begin{array}{l}m(u+v_0\cos \theta )+Mu=0\\ u=-\frac{m{v}_0\cos \theta }{m+M}\end{array}}$

El movimiento de la rana sobre la tabla es el tiro parabólico

${\displaystyle \overrightarrow{a}\{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\overrightarrow{v}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\overrightarrow{r}\{\begin{array}{l}x=v_0\cos \theta ·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

El tiempo de vuelo T hasta que la rana regresa a la tabla y=0 es

${\displaystyle T=\frac{2v_0\sin \theta }{g}}$

La rana se habrá desplazado sobre la tabla

${\displaystyle x=\frac{v_0^2\sin \left(2\theta \right)}{g}}$

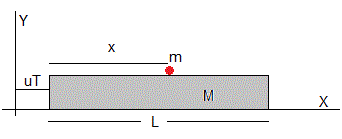
Como vemos en la figura, las posiciones de la tabla y de la rana respecto del estanque son.

${\displaystyle \begin{array}{l}{x}_t=ut\\ x_r=x_t+v_0\cos \theta t\end{array}}$

La posición del centro de masas en el instante t no cambia

${\displaystyle x_{cm}=\frac{M\left(ut+L/2\right)+m\left(ut+v_0\cos \theta ·t\right)}{m+M}=\frac{ML/2}{m+M}}$

En un sistema aislado si el centro de masas está inicialmente en reposo, seguirá en la misma posición.

El alcance, posición final de la rana respecto del estanque es

${\displaystyle x_r=uT+v_0\cos \theta ·T=\frac{M}{m+M}\frac{v_0\sin (2\theta )}{g}}$

La tabla estaba inicialmente en movimineto

Si la tabla estaba inicialmente en movimiento con velocidad V, la velocidad u de la tabla después que la rana salte es

${\displaystyle \begin{array}{l}m(u+v_0\cos \theta )+Mu=(m+M)V\hfill \\ u=V-\frac{m{v}_0\cos \theta }{m+M}\hfill \end{array}}$

El alcance respecto del estanque es

${\displaystyle x_r=uT+v_0\cos \theta ·T=\left(V+\frac{M}{m+M}{v}_0\cos \theta \right)\frac{2v_0\sin \theta }{g}}$

Ejemplo

• La masa de la rana, m=0.2 kg
• La masa de la tabla, M=1 kg
• La longitud de la tabla L=1 m
• El ángulo de tiro, θ=30°

La velocidad v₀ con la que debe saltar la rana para alcanzar el otro extremos de la tabla es

${\displaystyle L=\frac{v_0^2\sin \left(2\theta \right)}{g}}$

v₀=3.36 m/s

• El tiempo de vuelo, T=0.34 s
• La velocidad de la tabla, u=-0.48 m/s
• La posición de la tabla en este instante, uT=-0.167 m
• La posición de la rana, respecto al estanque, -0.167+1=0.833 m

La posición del centro de masas

${\displaystyle x_{cm}=\frac{0.2·0.833+1·(-0.167+0.5)}{1+0.2}=0.42\text{m}}$

que es la misma que la posición inicial

Actividades

Se introduce

• La masa m de la rana, en el control titulado Masa rana
• La velocidad v₀ de salto de la rana (respecto a la tabla), en el control titulado Velocidad
• El ángulo de disparo, θ en el control titulado Angulo
• La masa de la tabla se fijado en M=1 kg
• La longitud de la tabla se fijado en L=1 m

Se pulsa el botón titulado Nuevo

Observamos em movimiento de la rana y de la tabla. En la parte superior izquierda, se proporcionan los siguientes datos: tiempo, posición de la tabla y posición de la rana respecto de la tabla

Corriendo sobre una plataforma móvil

Sobre una plataforma de masa M inicialmente en reposo se sitúan n corredores de la misma masa m que se mueven con la misma velocidad sobre la plataforma. El corredor alcanza la velocidad u cuando llega al final de la plataforma y salta al suelo. Vamos a considerar dos casos

• Los corredores salen al mismo tiempo y saltan a la vez de la plataforma
• Los corredores salen secuencialmente, uno detrás del otro

Supondremos que la plataforma se mueve sin rozamiento sobre el plano horizontal

Simultáneamente

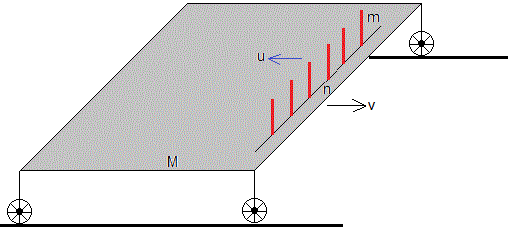
Cuando todos los corredores salen a la vez, la plataforma se mueve con velocidad v. La conservación del momento lineal se escribe

Mv+n·m(-u+v)=0

-u+v es la velocidad de los corredores respecto de Tierra. La velocidad final de la plataforma cuando todos los corredores han saltado es

${\displaystyle v=\frac{(n·m)u}{M+n·m}}$

Secuencialmente

Un situación diferente se produce cuando los corredores salen en diferentes momentos, por ejemplo cuando un corredor llega al final de la plataforma y salta, el siguiente empieza a correr

• Sale el primer corredor



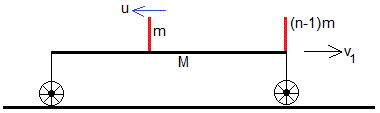
El momento lineal inicial del sistema es cero. El momento lineal del sistema cuando sale el primer corredor es también cero

${\displaystyle \begin{array}{l}\left(M+(n-1)m\right)v_1+m(-u+v_1)=0\\ v_1=\frac{mu}{M+nm}\end{array}}$

Esta es la velocidad final de la plataforma y de los (n-1) corredores que permanecen sobre ésta

• Sale el segundo corredor



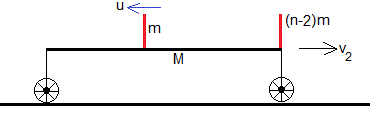
La conservación del momento lineal se escribe

${\displaystyle \begin{array}{l}\left(M+(n-2)m\right)v_2+m(-u+v_2)=\left(M+(n-1)m\right)v_1\\ v_2=v_1+\frac{mu}{M+(n-1)m}=mu\left(\frac{1}{M+nm}+\frac{1}{M+(n-1)m}\right)\end{array}}$

Esta es la velocidad final de la plataforma y de los (n-2) corredores que permanecen sobre ésta

• Sale el último corredor



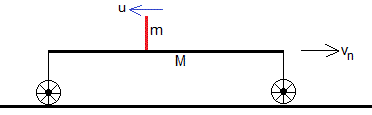
La conservación del momento lineal se escribe

${\displaystyle \begin{array}{l}M{v}_n+m(-u+v_n)=(M+m)v_{n-1}\\ v_n=v_{n-1}+\frac{mu}{M+m}=mu\left(\frac{1}{M+nm}+\frac{1}{M+(n-1)m}+\mathrm{....}\frac{1}{M+m}\right)\\ v_n=mu{\displaystyle \sum _{i=1}^n\frac{1}{M+i·m}}\end{array}}$

Esta es la velocidad final de la plataforma cuando todos los corredores han saltado secuencialmente

La velocidad final de la plataforma cuando los corredores corren secuencialmente es mayor que cuando corren simultáneamente

Referencias

Mario J Pinheiro. Some remarks about variable mass systems. Eur. J.Phys. 25 (2004) L5–L7,

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1114, pp. 193-195