Superficie parabólica

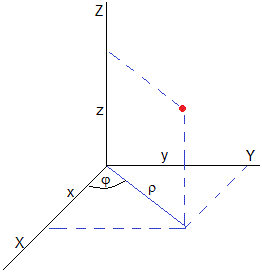
Consideremos una partícula de masa m que se mueve sobre una superficie parabólica de revolución de ecuación $z=\frac{1}{2}k{\rho }^2$, bajo la acción de su propio peso. En un instante dado t, las coordenadas de la partícula son (ρ, φ ,z). La posición de la partícula en dicho instante es

${\displaystyle \{\begin{array}{l}x=\rho \cos \phi \\ y=\rho \sin \phi \\ z=\frac{1}{2}k{\rho }^2\end{array}}$

Derivando con respecto del tiempo obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\frac{d\rho }{dt}\cos \phi -\rho \sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=\frac{d\rho }{dt}\sin \phi +\rho \cos \phi \frac{d\phi }{dt}\\ \frac{dz}{dt}=k\rho \frac{d\rho }{dt}\end{array}}$

La energía cinética es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\frac{1}{2}m\left({\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\\ \frac{1}{2}m\left(\left(1+k^2{\rho }^2\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)\end{array}}$

La energía potencial es

${\displaystyle V=mgz=\frac{1}{2}mgk{\rho }^2}$

La lagrangiana L=T-V es

${\displaystyle L=\frac{1}{2}m\left(\left(1+k^2{\rho }^2\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)-\frac{1}{2}mgk{\rho }^2}$

Ecuaciones del movimiento

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\rho }}\right)-\frac{\partial L}{\partial \rho }=0\hfill \\ \left(1+k^2{\rho }^2\right)\frac{d^2\rho }{d{t}^2}+k^2\rho {\left(\frac{d\rho }{dt}\right)}^2-\rho {\left(\frac{d\phi }{dt}\right)}^2+gk\rho =0\hfill \end{array}}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\hfill \\ {\rho }^2\frac{d^2\phi }{d{t}^2}=0\hfill \end{array}}$

Principios de conservación

Como la lagrangiana L es independiente de φ, obtenemos una cantidad h que se conserva

${\displaystyle {\rho }^2\frac{d\phi }{dt}=h}$

Comprobamos que h está relacionado con la componente Z del momento angular $\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}$

${\displaystyle L_z=m\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)=m{\rho }^2\frac{d\phi }{dt}}$

La primera ecuación del movimiento se convierte en

${\displaystyle \left(1+k^2{\rho }^2\right)\frac{d^2\rho }{d{t}^2}+k^2\rho {\left(\frac{d\rho }{dt}\right)}^2-\frac{h^2}{{\rho }^3}+gk\rho =0}$

que a su vez es la derivada con respecto del tiempo de una cantidad que se conserva, la energía

${\displaystyle \frac{1}{2}\frac{d}{dt}\left\{\left(1+k^2{\rho }^2\right){\left(\frac{d\rho }{dt}\right)}^2+\frac{h^2}{{\rho }^2}+gk{\rho }^2\right\}=0}$

La conservación de la energía ε se expresa

${\displaystyle \epsilon =\left(1+k^2{\rho }^2\right){\left(\frac{d\rho }{dt}\right)}^2+\frac{h^2}{{\rho }^2}+gk{\rho }^2}$

Para un valor dado de ε el movimiento en la dirección radial tiene lugar entre las distancias ρ₁ y ρ₂ dados por las soluciones de la ecuación

${\displaystyle \epsilon =\frac{h^2}{{\rho }^2}+gk{\rho }^2}$

Trayectoria sobre la superficie parabólica

Para representar la trayectoria seguida por la partícula, partimos de la posición ρ=ρ₁ en el que se cumple que dρ/dt=0, establecemos φ=0. Determinamos la constante h a partir de los datos de ρ₁ y ρ₂.

${\displaystyle \begin{array}{l}\epsilon =\frac{h^2}{{\rho }_1^2}+gk{\rho }_1^2=\frac{h^2}{{\rho }_2^2}+gk{\rho }_2^2\\ h=\sqrt{gk}{\rho }_2{\rho }_1\end{array}}$

Integramos las dos ecuaciones diferenciales con las condiciones iniciales señaladas para obtener la trayectoria ρ=ρ(φ) sobre la superficie parabólica.

${\displaystyle \begin{array}{l}\left(1+k^2{\rho }^2\right)\frac{d^2\rho }{d{t}^2}+k^2\rho {\left(\frac{d\rho }{dt}\right)}^2-\frac{h^2}{{\rho }^3}+gk\rho =0\\ {\rho }^2\frac{d\phi }{dt}=h\end{array}}$

k=0.5; %superficie parabólica
r1=1;
r2=4; %radios mínimo y máximo
%cuadrado del moemnto angular Lz
h2=9.8*k*r2^2*r1^2; 
x0=[r1,0,0]; %condiciones iniciales
tspan=[0,20];
% x(1)=r, x(2)=dr/dt,x(3)=phi
fg=@(t,x)[x(2);(-k^2*x(1)*x(2)^2+h2/x(1)^3-9.8*k*x(1))/(1+k^2*x(1)^2); 
sqrt(h2)/x(1)^2];
[t,x]=ode45(fg,tspan,x0);
xp=x(:,1).*cos(x(:,3));
yp=x(:,1).*sin(x(:,3));
zp=k*x(:,1).^2/2;
 
hold on
view(130,80)
%superficie cónica
phi=linspace(0,2*pi,40);
r=linspace(0,4);
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi);
y=r.*sin(phi);
z=k*r.^2/2;
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
 
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
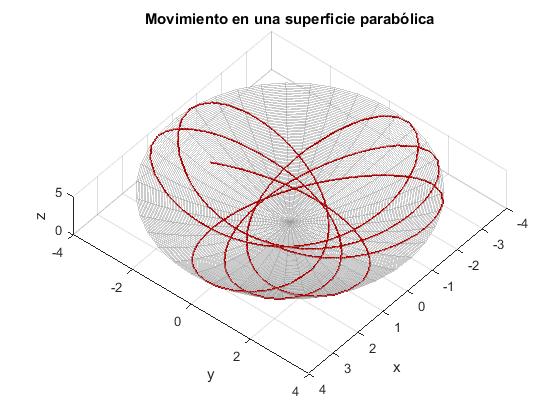
title('Movimiento en una superficie parabólica')

Superficie general

Consideremos una partícula de masa m que se mueve sobre una superficie de revolución de ecuación z=kρⁿ, bajo la acción de su propio peso. En un instante dado t, las coordenadas de la partícula son (ρ, φ, z). La posición de la partícula en dicho instante es

${\displaystyle \{\begin{array}{l}x=\rho \cos \phi \\ y=\rho \sin \phi \\ z=k{\rho }^n\end{array}}$

Derivando con respecto del tiempo obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\frac{d\rho }{dt}\cos \phi -\rho \sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=\frac{d\rho }{dt}\sin \phi +\rho \cos \phi \frac{d\phi }{dt}\\ \frac{dz}{dt}=nk{\rho }^{n-1}\frac{d\rho }{dt}\end{array}}$

La energía cinética es

${\displaystyle T=\frac{1}{2}m{\left({\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2+\left(\frac{dz}{dt}\right)\right)}^2=\frac{1}{2}m\left(\left(1+n^2{k}^2{\rho }^{2(n-1)}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)}$

La energía potencial es

${\displaystyle V=mgz=mgk{\rho }^n}$

La lagrangiana L=T-V es

${\displaystyle L=\frac{1}{2}m\left(\left(1+n^2{k}^2{\rho }^{2(n-1)}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)-mgk{\rho }^n}$

Ecuaciones del movimiento

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\rho }}\right)-\frac{\partial L}{\partial \rho }=0\hfill \\ \left(1+n^2{k}^2{\rho }^{2n-2}\right)\frac{d^2\rho }{d{t}^2}+k^2{\rho }^{2n-3}{n}^2\left(n-1\right){\left(\frac{d\rho }{dt}\right)}^2-\rho {\left(\frac{d\phi }{dt}\right)}^2+gkn{\rho }^{n-1}=0\hfill \end{array}}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ \frac{d}{dt}\left(m{\rho }^2\frac{d\phi }{dt}\right)=0\\ m{\rho }^2\frac{d\phi }{dt}=L_z\end{array}}$

La componente L_z del momento angular es constante. Denominamos h=L_z/m

La energía se conserva

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left(\left(1+n^2{k}^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)+mgk{\rho }^n\hfill \\ \frac{E}{m}=\frac{1}{2}\left(\left(1+n^2{k}^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+\frac{h^2}{{\rho }^2}\right)+gk{\rho }^n\hfill \end{array}}$

Trayectoria sobre la superficie parabólica

Para representar la trayectoria seguida por la partícula, partimos de la posición ρ=ρ₁ en el que se cumple que dρ/dt=0, establecemos φ=0. Determinamos la constante h a partir de los datos de ρ₁ y ρ₂.

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{h^2}{{\rho }_1^2}+gk{\rho }_1^n=\frac{1}{2}\frac{h^2}{{\rho }_2^2}+gk{\rho }_2^n\\ h^2=\frac{2{\rho }_1^2{\rho }_2^{2}gk\left({\rho }_2^n-{\rho }_1^n\right)}{{\rho }_2^2-{\rho }_1^2}\end{array}}$

Integramos las dos ecuaciones diferenciales con las condiciones iniciales señaladas para obtener la trayectoria ρ=ρ(φ) sobre la superficie parabólica.

${\displaystyle \{\begin{array}{l}\left(1+n^2{k}^2{\rho }^{2n-2}\right)\frac{d^2\rho }{d{t}^2}+k^2{\rho }^{2n-3}{n}^2\left(n-1\right){\left(\frac{d\rho }{dt}\right)}^2-\frac{h^2}{{\rho }^3}+gkn{\rho }^{n-1}=0\\ {\rho }^2\frac{d\phi }{dt}=h\end{array}}$

k=0.25; %superficie parabólica
r1=1;
r2=4; %radios mínimo y máximo
%cuadrado del momento angular Lz
h2=2*9.8*k*r2^2*r1^2*(r2^n-r1^n)/(r2^2-r1^2); 
n=2.5;
x0=[r1,0,0]; %condiciones iniciales
tspan=[0,40];
% x(1)=r, x(2)=dr/dt,x(3)=phi
fg=@(t,x)[x(2);(-k^2*x(1)^(2*n-3)*n^2*(n-1)*x(2)^2+h2/x(1)^3-
9.8*k*n*x(1)^(n-1))/(1+n^2*k^2*x(1)^(2*n-2)); sqrt(h2)/x(1)^2];
[t,x]=ode45(fg,tspan,x0);
xp=x(:,1).*cos(x(:,3));
yp=x(:,1).*sin(x(:,3));
zp=k*x(:,1).^n;
%energía
e=((1+n^2*k^2*x(:,1).^(2*n-2)).*x(:,2).^2+h2./x(:,1).^2)/2+9.8*k*x(:,1).^n;

hold on
view(130,80)
%superficie general
phi=linspace(0,2*pi,40);
r=linspace(0,4.5);
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi);
y=r.*sin(phi);
z=k*r.^n;
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
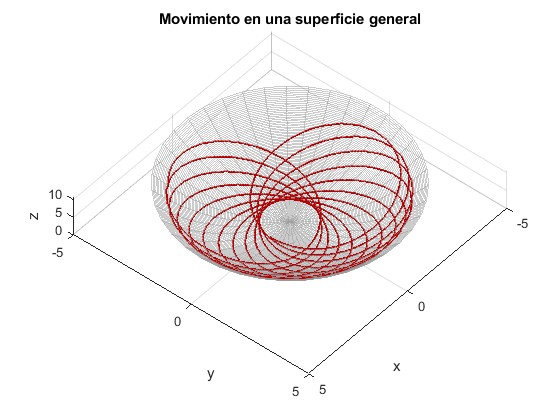
title('Movimiento en una superficie general')

Comprobamos que la energía se mantiene constante

e =
   83.4633
   83.4633
   83.4633
   ......
   85.1522
   85.1521
   85.1523

Referencias

Sean A. Genis, Carl E. Mungan. Orbits on a concave frictionless surface. Washington Academy of Sciences, summer 2007

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/EJP17.pdf

D. G. Gómez-Pérez, O. González-Amezcua. The motion of a particle on the surface of a general cone. Revista Mexicana de Física E 21 010206 1–5 January-June 2024