Movimiento en una superficie de revolución <em>-k/r</em>

Movimiento en una superficie de revolución -k/r

Los simuladores de las órbitas de un planeta consisten en una superficie de revolución con la forma del potencial -k/r, sobre la cual rueda una bolita de acero. Se pueden ver algunos ejemplos en YouTube, https://www.youtube.com/watch?v=3oGlg7AaeAw

Energía

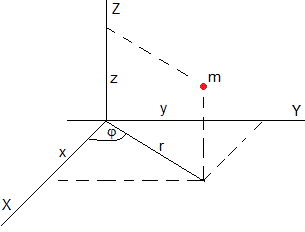
En coordendas cilíndricas, la posición y velocidad de una partícula se escriben

$\begin{array}{l} \vec{r} {\begin{cases} x = r \cos φ \\ y = r \sin φ \\ z \end{cases} \\ \vec{v} {\begin{cases} \frac{d x}{d t} = \frac{d r}{d t} \cos φ - r \sin φ \frac{d φ}{d t} \\ \frac{d y}{d t} = \frac{d r}{d t} \sin φ + r \cos φ \frac{d φ}{d t} \\ \frac{d z}{d t} \end{cases} \end{array}$

La energía cinética de una esfera de masa m y radio R que rueda sin deslizar sobre una superficie es la suma de dos términos: traslación del centro de masa y rotación alrededor de un eje que pasa por el c.m.

$E_{k} = \frac{1}{2} m v^{2} + \frac{1}{2} (\frac{2}{5} m R^{2}) {(\frac{v}{R})}^{2} = \frac{1}{2} (\frac{7}{5} m) v^{2}$

Cuando rueda sin deslizar, la velocidad de traslación del c.m. y de rotación están relacionadas. La energía cinética se expresa en coordenadas cilíndricas

La energía cinética se expresa en coordenadas cilíndricas

$E_{k} = \frac{1}{2} (\frac{7}{5} m) ({(\frac{d r}{d t})}^{2} + r^{2} {(\frac{d φ}{d t})}^{2} + {(\frac{d z}{d t})}^{2})$

Llamemos a M=7m/5

Cuando el cuerpo se encuentra a una altura z por encima del pano horizontal XY su energía potencial es E_p=mgz.

La energía total es constante

$E = \frac{1}{2} M ({(\frac{d r}{d t})}^{2} + r^{2} {(\frac{d φ}{d t})}^{2} + {(\frac{d z}{d t})}^{2}) + m g z$

Ecuaciones del movimiento

La lagrangiana L=E_k-E_p es

$L = \frac{1}{2} M ({(\frac{d r}{d t})}^{2} + r^{2} {(\frac{d φ}{d t})}^{2} + {(\frac{d z}{d t})}^{2}) - m g z$

La lagrangiana L no depende del ángulo φ, se conserva una magnitud que denominaremos l

$\begin{array}{l} \frac{d}{d t} (\frac{\partial L}{\partial \dot{φ}}) = 0 \\ M r^{2} \frac{d φ}{d t} = l \end{array}$

Para deducir la ecuación del movimiento en la dirección radial, como z es función de r, precisamos las relaciones

$\begin{array}{l} \frac{d z}{d t} = \frac{d z}{d r} \frac{d r}{d t} = \frac{d z}{d r} \dot{r} \\ \frac{d}{d t} (\frac{d z}{d r}) = \frac{d}{d r} (\frac{d z}{d r}) \frac{d r}{d t} = \frac{d^{2} z}{d r^{2}} \dot{r} \\ \frac{d}{d r} (\frac{d z}{d t}) = \frac{d}{d r} (\frac{d z}{d r} \frac{d r}{d t}) = \frac{d^{2} z}{d r^{2}} \dot{r} \end{array}$

Calculamos por separado, los dos términos de la ecuación del movimiento en la dirección radial

$\frac{d}{d t} (\frac{\partial L}{\partial \dot{r}}) - \frac{\partial L}{\partial r} = 0$

El primer término vale

$\begin{array}{l} \frac{\partial L}{\partial \dot{r}} = M \frac{d r}{d t} + M (\frac{d z}{d r} \frac{d r}{d t}) (\frac{d z}{d r}) = M \frac{d r}{d t} + M {(\frac{d z}{d r})}^{2} (\frac{d r}{d t}) \\ \frac{d}{d t} (\frac{\partial L}{\partial \dot{r}}) = M \frac{d^{2} r}{d t^{2}} + 2 M (\frac{d z}{d r}) {(\frac{d r}{d t})}^{2} (\frac{d^{2} z}{d r^{2}}) + M {(\frac{d z}{d r})}^{2} (\frac{d^{2} r}{d t^{2}}) = \\ M (1 + {(\frac{d z}{d r})}^{2}) \frac{d^{2} r}{d t^{2}} + 2 M (\frac{d z}{d r}) {(\frac{d r}{d t})}^{2} (\frac{d^{2} z}{d r^{2}}) \end{array}$

El segundo término

$\begin{array}{l} \frac{\partial L}{\partial r} = M r {(\frac{d φ}{d t})}^{2} + M (\frac{d z}{d t}) (\frac{d^{2} z}{d r^{2}}) (\frac{d r}{d t}) - m g \frac{d z}{d r} = \\ M r {(\frac{d φ}{d t})}^{2} + M (\frac{d r}{d t}) (\frac{d^{2} z}{d r^{2}}) {(\frac{d r}{d t})}^{2} - m g \frac{d z}{d r} \end{array}$

Agrupando los dos términos

$M (1 + {(\frac{d z}{d r})}^{2}) \frac{d^{2} r}{d t^{2}} + M (\frac{d z}{d r}) (\frac{d^{2} z}{d r^{2}}) {(\frac{d r}{d t})}^{2} - M r {(\frac{d φ}{d t})}^{2} + m g \frac{d z}{d r} = 0$

Eliminamos el ángulo φ entre las dos ecuaciones del movimiento

$\begin{array}{l} M (1 + {(\frac{d z}{d r})}^{2}) \frac{d^{2} r}{d t^{2}} + M (\frac{d z}{d r}) (\frac{d^{2} z}{d r^{2}}) {(\frac{d r}{d t})}^{2} - \frac{l^{2}}{M^{2} r^{3}} + m g \frac{d z}{d r} = 0 \\ (1 + {(\frac{d z}{d r})}^{2}) \frac{d^{2} r}{d t^{2}} + (\frac{d z}{d r}) (\frac{d^{2} z}{d r^{2}}) {(\frac{d r}{d t})}^{2} - \frac{25 l^{2}}{49 m^{2} r^{3}} + \frac{5}{7} g \frac{d z}{d r} = 0 \end{array}$

Como vemos difiere de la ecuación del movimiento en la dirección radial de un cuerpo bajo la acción de una fuerza central y conservativa inversamente proporcional al cuadrado de las distancias

$\frac{d^{2} r}{d t^{2}} - \frac{l^{2}}{m^{2} r^{3}} + \frac{G M}{r^{2}} = 0$

Ecuación de la trayectoria

Eliminamos el tiempo t, expresando la ecuación diferencial en términos de las variables u=1/r y φ, teniendo en cuenta la conservación de la magnitud l en la primera ecuación del movimiento

$\begin{array}{l} M r^{2} \frac{d φ}{d t} = l \\ \frac{d φ}{d t} = u^{2} \frac{5 l}{7 m} \end{array}$

Precisamos de las siguientes relaciones

$\begin{array}{l} u = \frac{1}{r} \\ \frac{d r}{d t} = - \frac{1}{u^{2}} \frac{d u}{d t} = - \frac{1}{u^{2}} \frac{d u}{d φ} \frac{d φ}{d t} = - \frac{5 l}{7 m} \frac{d u}{d φ} \\ \frac{d}{d t} (\frac{d r}{d t}) = \frac{d}{d φ} (- \frac{5 l}{7 m} \frac{d u}{d φ}) \frac{d φ}{d t} = - \frac{25 l^{2}}{49 m^{2}} u^{2} \frac{d^{2} u}{d φ^{2}} \end{array}$

La ecuación del movimiento en la dirección radial se transforma en

$\begin{array}{l} (1 + {(\frac{d z}{d r})}^{2}) (- \frac{25 l^{2}}{49 m^{2}} u^{2} \frac{d^{2} u}{d φ^{2}}) + (\frac{d z}{d r}) (\frac{d^{2} z}{d r^{2}}) {(- \frac{5 l}{7 m} \frac{d u}{d φ})}^{2} - \frac{25 l^{2}}{49 m^{2}} u^{3} + \frac{5}{7} g \frac{d z}{d r} = 0 \\ - (1 + {(\frac{d z}{d r})}^{2}) (u^{2} \frac{d^{2} u}{d φ^{2}}) + (\frac{d z}{d r}) (\frac{d^{2} z}{d r^{2}}) {(\frac{d u}{d φ})}^{2} - u^{3} + \frac{7 m^{2}}{5 l^{2}} g \frac{d z}{d r} = 0 \end{array}$

Dada la función z=f(r), obtenemos distintas ecuaciones diferenciales que describen el movimiento de una bolita que rueda sin deslizar sobre la superficie de revolución descrita por dicha función

Inversamente proporcional a r

La superficie de revolución es inversamente proporcional a la distancia r al eje

$\begin{array}{l} z = - \frac{k}{r} \\ \frac{d z}{d r} = \frac{k}{r^{2}} = k u^{2} \\ \frac{d^{2} z}{d r^{2}} = - 2 \frac{k}{r^{3}} = - 2 k u^{3} \end{array}$

La ecuación diferencial de las trayectorias del centro de masa de la bolita es

$\begin{array}{l} - (1 + {(k u^{2})}^{2}) (u^{2} \frac{d^{2} u}{d φ^{2}}) + (k u^{2}) (- 2 k u^{3}) {(\frac{d u}{d φ})}^{2} - u^{3} + \frac{7 m^{2}}{5 l^{2}} g (k u^{2}) = 0 \\ (1 + k^{2} u^{4}) (\frac{d^{2} u}{d φ^{2}}) + 2 k^{2} u^{3} {(\frac{d u}{d φ})}^{2} + u - \frac{7 m^{2}}{5 l^{2}} k g = 0 \end{array}$

El caso más simple, resolvemos la ecuación diferencial con k=1 y el término constante igual a la unidad

$(1 + u^{4}) (\frac{d^{2} u}{d φ^{2}}) + 2 u^{3} {(\frac{d u}{d φ})}^{2} + u - 1 = 0$

con la condición inicial de que para φ=0 u=u₀, du/dφ=0, es decir, la velocidad inicial en la dirección radial es nula, parte del reposo.

k=1;
c=1; 

x0=[1.7,0]; %condiciones iniciales
tf=14*pi;
% x(1)=u, x(2)=du/dphi, t es phi
fg=@(t,x)[x(2); (-2*k^2*x(1)^3*x(2)^2-x(1)+c)/(1+k^2*x(1)^4)];
[t,x]=ode45(fg,[0,tf],x0);
xp=cos(t)./x(:,1);
yp=sin(t)./x(:,1);
zp=-x(:,1);
hold on
r=linspace(0.5,4,50);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=1./r;
%mesh(x,y,-z)
surfl(x,y,-z)
shading interp
colormap(gray);

%trayectoria
h1=line(xp,yp,zp);
%set(h1,'Color',[.7,0,0],'LineWidth',1.5)
set(h1,'Color',[.7,0,0])
 
hold off
view(108,46)
grid on
xlabel('x')
ylabel('y')
zlabel('z')
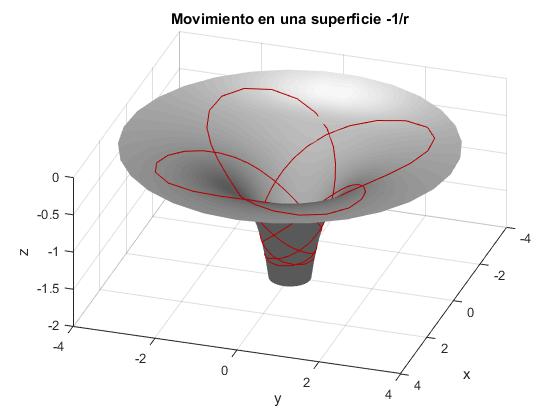
title('Movimiento en una superficie -1/r')

Referencias

L. Q. English Trajectories of rolling marbles on various funnels. Am. J. Phys. 80 811) November 2012, pp. 996-1000