Movimiento de una partícula unida a un muelle elástico a lo largo de una elipse vertical
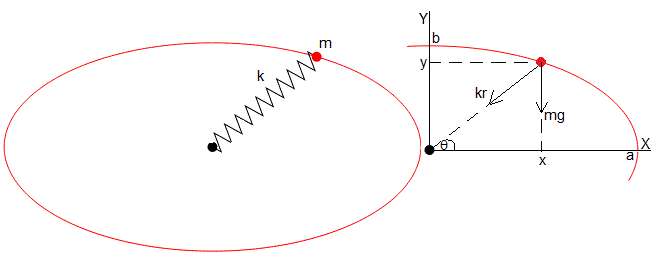
Equilibrio y estabilidad
Establecemos el origen del Sistema de Referencia en el centro de la elipse de semiejes a y b. Las coordenadas de la partícula son: x=a·cosθ, y=a·sinθ
La distancia r de la partícula al origen es
La partícula está bajo la influencia de dos fuerzas conservativas: el peso mg y la acción del muelle elástico kr. Las energías potenciales correspondientes a estas dos fuerzas son:
Los puntos de equilibrio se obtienen cuando la energía potencial V es un extremo
Una solución es cosθ=0, θ=±π/2. La otra solución
Calculamos la derivada segunda, para determinar si una posición de equilibrio es estable o inestable
La posición de equilibrio es estable si la derivada segunda es positiva (mínimo de V), en caso contrario, la posición de equilibrio sería inestable (máximo)
Para θ=π/2
Para θ=-π/2
Para
Por tanto, el ángulo θ1 corresponde a un máximo
Representación gráfica de la energía potencial V
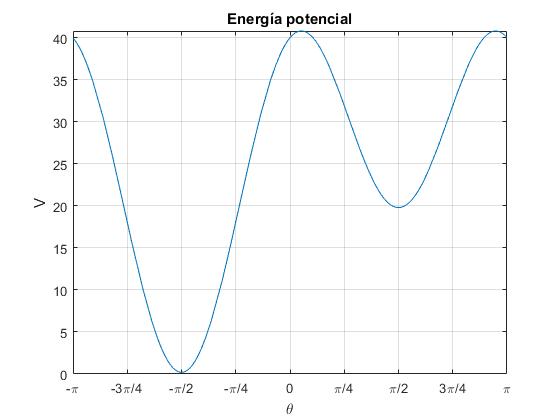
Representamos la energía potencial V en función de la posición angular θ.
Sea el semieje mayor a=2, el semieje menor b=1 y el cociente k/m=20. Vemos que para θ=π/2, θ=-π/2 la energía potencial V presenta un mínimo y para los ángulos θ1=9.4° y 180-θ1=170.6° presenta un máximo
a=2; %semieje mayor
b=1; %semieje menor
k=20; %cociente k/m
V=@(x) 9.8*b*sin(x)+k*((a*cos(x)).^2+(b*sin(x)).^2)/2;
fplot(V,[-pi,pi])
set(gca,'XTick',-pi:pi/4:pi)
set(gca,'XTickLabel',{'-\pi','-3\pi/4','-\pi/2','-\pi/4','0'
,'\pi/4','\pi/2','3\pi/4','\pi' })
xlabel('\theta')
ylabel('V')
title('Energía potencial')
grid on
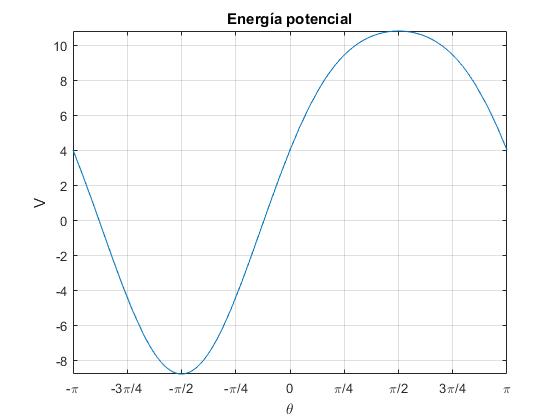
Sea el semieje mayor a=2, el semieje menor b=1, y el cociente k/m=2. Vemos que para θ=-π/2 la energía potencial V presenta un mínimo y para θ=π/2 un máximo. El ángulo θ1 no existe.
Ecuación del movimiento
Dada la posición de la partícula, x=a·cosθ, y=a·sinθ, derivando respecto del tiempo obtenemos las componentes de su velocidad
La energía cinética T es
La lagrangiana L=T-V y la ecuación del movimiento son
Resolvemos la ecuación diferencial del movimiento con las siguientes condiciones iniciales, en el instante t=0, θ=θ0, dθ/dt=0
a=2; %semieje mayor
b=1; %semieje menor
k=2; %cociente k/m
x0=[-80*pi/180,0];
f=@(t,x) [x(2); ((k-x(2)^2)*sin(x(1))*cos(x(1))*(a^2-b^2)-9.8*b*cos(x(1)))
/((a*sin(x(1)))^2+(b*cos(x(1)))^2)];
[t,x]=ode45(f,[0,12],x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Posición angular en función del tiempo')
%la energía se mantiene constante
E=9.8*b*sin(x(:,1))+k*((a*cos(x(:,1))).^2+(b*sin(x(:,1))).^2)/2+
((a*sin(x(:,1))).^2+(b*cos(x(:,1))).^2).*(x(:,2).^2)/2;
El ángulo inicial θ=-80° es próximo al de equilibrio estable, -π/2. La partícula describe una oscilación en torno a dicho punto con un determinado periodo, que se puede medir en la ventana gráfica
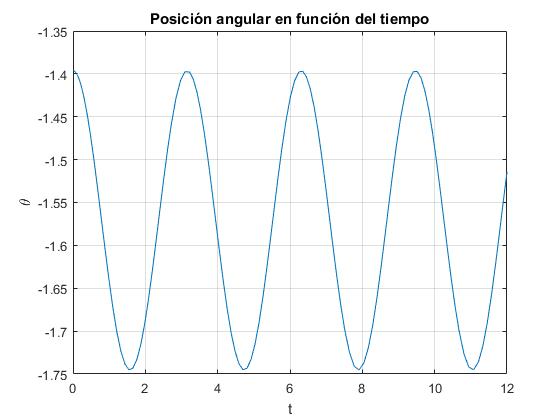
El procedimiento numérico ode45, no resuelve adecuadamente la ecuación diferencial para la posición θ=80°, próxima a la de equilibrio inestable π/2, (muy lejos del equilibrio estable, -π/2), el procedimiento ode15s, lo resuelve mejor
Actividades
Se introduce
- El semieje mayor a de la elipse, en el control titulado Semieje mayor
- El semieje menor de la elipse se ha fijado en b=1
- El cociente entre la constante elástica del muelle y la masa de la partícula, k/m, en el control titulado Constante
- La posición inicial de la partícula θ0 en el instante t=0, en el control titulado Angulo inicial en grados
- Se ha fijado la velocidad inicial de la partícula en dθ/dt=0
Se pulsa el botón titulado Nuevo
En la parte superior de la ventana gráfica se muestra el tiempo t, el ángulo θ y la velocidad angular dθ/dt.
Se calcula la energía total E/m que permanece constante
Referencias
Ahmad A. Kamal. 1000 Solved Problems in Classical Physics. An Exercise Book. Springer Verlag 2011. Problema 7.30, enunciado, 294, solución, 331

