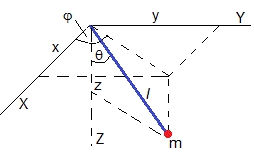
Consideramos el movimiento de un péndulo de longitud l que se puede mover en todas las direcciones del espacio bajo la acción de su propio peso. En un instante dado t, la partícula dista l del centro de oscilación y hace un ángulo φ con el eje X y un ángulo θ con el eje Z, tal como se muestra en la figura. Describimos el movimiento de la partícula en coordenadas esféricas (r, φ, θ) con el radio r=l constante.

La posición de la partícula es

${\displaystyle \{\begin{array}{l}x=l\sin \theta \cos \phi \\ y=l\sin \theta \sin \phi \\ z=l\cos \theta \end{array}}$

Derivando con respecto del tiempo obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=l\cos \theta \frac{d\theta }{dt}\cos \phi -l\sin \theta \sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=l\cos \theta \frac{d\theta }{dt}\sin \phi +l\sin \theta \cos \phi \frac{d\phi }{dt}\\ \frac{dz}{dt}=-l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\frac{1}{2}m{l}^2\left({\left(\frac{d\theta }{dt}\right)}^2+{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)}$

La energía potencial es V=-mgz=-mglcosθ

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m{l}^2\left({\left(\frac{d\theta }{dt}\right)}^2+{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)+mgl\cos \theta \\ L=\frac{1}{2}m{l}^2\left({\dot{\theta }}^2+{\sin }^2\theta ·{\dot{\phi }}^2\right)+mgl\cos \theta \end{array}}$

Ecuaciones del movimiento

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ l\frac{d^2\theta }{d{t}^2}-l\sin \theta \cos \theta {\left(\frac{d\phi }{dt}\right)}^2+g\sin \theta =0\end{array}}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ \frac{d}{dt}\left(m{l}^2{\sin }^2\theta \frac{d\phi }{dt}\right)=0\end{array}}$

Principios de conservación

Como la lagrangiana L es independiente de φ, obtenemos una cantidad h que se conserva

${\displaystyle {\sin }^2\theta \frac{d\phi }{dt}=h}$

Comprobamos que h está relacionado con la componente Z del momento angular $\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}$

${\displaystyle L_z=m\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)=m{l}^2{\sin }^2\theta \frac{d\phi }{dt}}$

Llamamos ${\omega }_0^2=g/l$ a la frecuencia natural de la oscilación de un péndulo simple. La primera ecuación se convierte en

${\displaystyle \frac{d^2\theta }{d{t}^2}-\frac{h^2}{{\sin }^3\theta }\cos \theta +{\omega }_0^2\sin \theta =0}$

que a su vez es la derivada con respecto del tiempo de una cantidad que se conserva

${\displaystyle \frac{d}{dt}\left(\frac{1}{2}{\left(\frac{d\theta }{dt}\right)}^2+\frac{h^2}{2{\sin }^2\theta }-{\omega }_0^2\cos \theta \right)=0}$

La conservación de la energía ε se expresa

${\displaystyle \frac{1}{2}{\left(\frac{d\theta }{dt}\right)}^2+\frac{h^2}{2{\sin }^2\theta }-{\omega }_0^2\cos \theta =\epsilon }$

Donde V(θ) es la energía potencial efectiva.

${\displaystyle V(\theta )=\frac{h^2}{2{\sin }^2\theta }-{\omega }_0^2\cos \theta }$

Para un valor dado de ε mayor que el mínimo V(θ_m), el movimiento tiene lugar entre los ángulos θ₁ y θ₂ dados por las soluciones de la ecuación cúbica

${\displaystyle \begin{array}{l}\epsilon =\frac{h^2}{2{\sin }^2\theta }-{\omega }_0^2\cos \theta \\ {\cos }^3\theta +\frac{\epsilon }{{\omega }_0^2}{\cos }^2\theta -\cos \theta +\frac{h^2-2\epsilon }{2{\omega }_0^2}=0\end{array}}$

Las raíces de la ecuación cúbica se pueden calcular con roots de MATLAB o la función raices_3 definida en la página titulada Raíces de una ecuación (I)

R=1; %longitud del péndulo
w0=sqrt(9.8/R); %frecuencia natural de oscilación
h2=21.1; % cuadrado del momento angular, Lz
energia=37.3; %energía
f=@(x) h2./(2*sin(x).^2)-w0^2*cos(x);
fplot(f,[pi/12,pi-pi/12],'color','r')
line([0,pi],[energia, energia],'color','k')
g=@(x) f(x)-energia;

%raíces
th=zeros(1,2);
cth=raices_3([1,energia/w0^2,-1,(h2-2*energia)/(2*w0^2)]);
j=1;
for i=1:length(cth)
    if abs(cth(i))>=1 
        continue;
    end
    th(j)=acos(cth(i));
    j=j+1;
end     
line([th(1),th(1)],[0,energia], 'lineStyle','--')
line([th(2),th(2)],[0,energia],'lineStyle','--')
ylim([0,40])
xlim([0,2.7])
grid on
xlabel('\theta')
ylabel('V(\theta)')
title('Energía potencial')

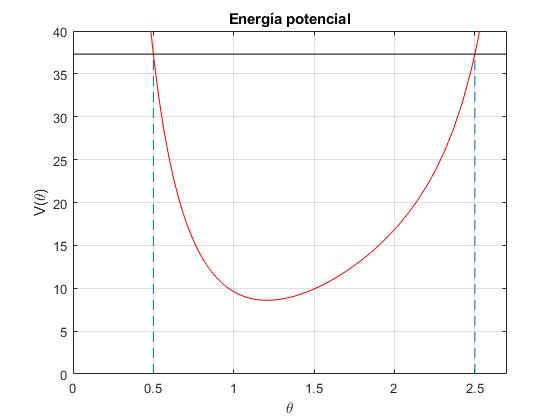
El mínimo de la energía potencial efectiva V(θ) se calcula derivando con respecto a θ e igualando a cero

${\displaystyle \frac{dV(\theta )}{d\theta }=-h^2\frac{\cos \theta }{{\sin }^3\theta }+{\omega }_0^2\sin \theta }$

El ángulo correspondiente al mínimo θ_m es la raíz real y positiva de la ecuación

${\displaystyle \begin{array}{l}{\omega }_0^2{\sin }^4\theta -h^2\cos \theta =0\\ {\cos }^4\theta -2{\cos }^2\theta -\frac{h^2}{{\omega }_0^2}\cos \theta +1=0\end{array}}$

>> roots([1,0,-2,-h2/w0^2,1])
ans =
   1.7081 + 0.0000i
  -1.0315 + 0.7654i
  -1.0315 - 0.7654i
   0.3549 + 0.0000i
>> th_m=acos(0.3549)
th_m =    1.2080

Calculamos la derivada segunda y verificamos que la posición θ_m corresponde a un mínimo

${\displaystyle \begin{array}{l}\frac{d^{2}V(\theta )}{d{\theta }^2}=-h^2\frac{-{\sin }^4\theta -3{\sin }^2\theta ·{\cos }^2\theta }{{\sin }^6\theta }+{\omega }_0^2\cos \theta =h^2\frac{1+2{\cos }^2\theta }{{\sin }^4\theta }+{\omega }_0^2\cos \theta \\ {\frac{d^{2}V(\theta )}{d{\theta }^2}|}_{\theta ={\theta }_m}=h^2\frac{1+2{\cos }^2{\theta }_m}{\frac{h^2}{{\omega }_0^2}\cos {\theta }_m}+{\omega }_0^2\cos {\theta }_m={\omega }_0^2\frac{1+3{\cos }^2{\theta }_m}{\cos {\theta }_m}>0\end{array}}$

El valor del mínimo V(θ_m) es

${\displaystyle V\left({\theta }_m\right)=\frac{h^2}{2{\sin }^2{\theta }_m}-{\omega }_0^2\cos {\theta }_m}$

>> f(th_m)
ans =    8.5923

Caso particular

Un caso particular importante se produce cuando h²=2ε. Una de las raíces es cosθ₁=0, θ₁=π/2. La otra posición de retorno θ₂ es la raíz positiva de la ecuación de segundo grado

${\displaystyle {\cos }^2\theta +\frac{\epsilon }{{\omega }_0^2}\cos \theta -1=0}$

Cuando $\epsilon ={\omega }_0^2$, se obtiene el número áureo

${\displaystyle \cos {\theta }_2=\frac{-1+\sqrt{5}}{2}}$

Trayectoria de la partícula

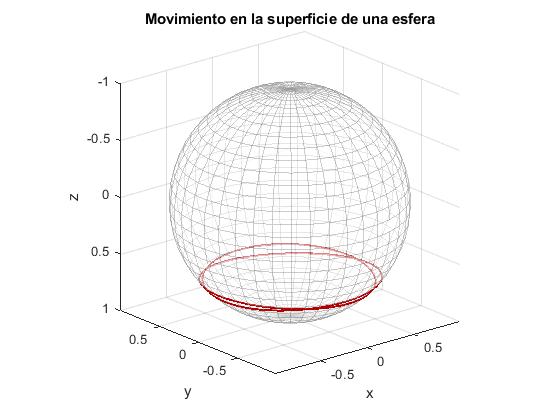
Dada la energía ε y del momento angular h, calculamos las posiciones de retorno θ₁ y θ₂. En este apartado, los datos son las posiciones de retorno

Para representar la trayectoria seguida por la partícula, partimos de la posición angular θ=θ₁ en el que se cumple que dθ/dt=0, establecemos φ=0. Determinamos la constante h a partir de los datos de θ₁ y θ₂. Igualando V(θ₁)=V(θ₂)=ε, obtenemos

${\displaystyle \begin{array}{l}\epsilon =\frac{h^2}{2{\sin }^2{\theta }_1}-{\omega }_0^2\cos {\theta }_1=\frac{h^2}{2{\sin }^2{\theta }_2}-{\omega }_0^2\cos {\theta }_2\\ h^2={\omega }_0^2\frac{{\sin }^2{\theta }_1{\sin }^2{\theta }_2}{\cos \left(\frac{{\theta }_1+{\theta }_2}{2}\right)\cos \left(\frac{{\theta }_1-{\theta }_2}{2}\right)}\end{array}}$

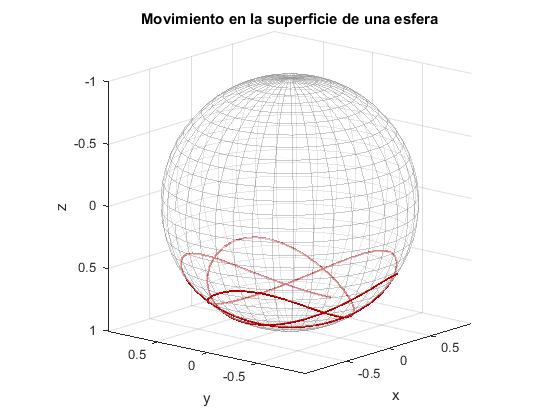
Integramos las dos ecuaciones diferenciales con las condiciones iniciales señaladas para obtener la trayectoria θ=θ(φ) en la superficie esférica de radio l

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=\frac{h^2}{{\sin }^3\theta }\cos \theta -{\omega }_0^2\sin \theta \hfill \\ \frac{d\phi }{dt}=\frac{h}{{\sin }^2\theta }\hfill \end{array}}$

R=1; %longitud del péndulo
w0=sqrt(9.8/R); %frecuencia natural de oscilación
th_1=pi/6; %angulos mínimo y máximo
th_2=pi/3;
h2=w0^2*sin(th_1)^2*sin(th_2)^2/(cos((th_1+th_2)/2)*cos((th_1-th_2)/2));
x0=[th_1,0,0]; %condiciones iniciales
tspan=[0,5];
% x(1)=th, x(2)=dth/dt,x(3)=phi
fg=@(t,x)[x(2); h2*cos(x(1))/(sin(x(1))^3)-w0^2*sin(x(1)); sqrt(h2)/sin(x(1))^2];
[t,x]=ode45(fg,tspan,x0);
xp=R*sin(x(:,1)).*cos(x(:,3));
yp=R*sin(x(:,1)).*sin(x(:,3));
zp=R*cos(x(:,1));

%esfera
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
axis equal

%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
set(gca,'zDir','reverse')
view (-40,20)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en la superficie de una esfera')

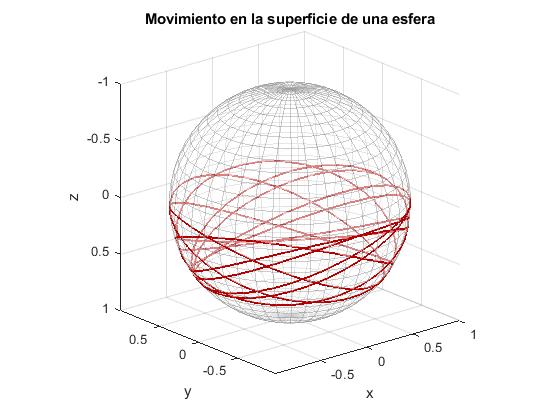
Cambiamos los ángulos θ₁ y θ₂

...
th_1=pi/2;
th_2=acos((-1+sqrt(5))/2); %angulos mínimo y máximo
tspan=[0,10];
...

Péndulo simple

Si φ=φ₀=constante, dφ/dt=0, h=0

${\displaystyle \frac{d^2\theta }{d{t}^2}+{\omega }_0^2\sin \theta =0}$

Obtenemos la ecuación diferencial del péndulo simple que oscila en el plano φ₀

Trayectorias casi circulares

Un péndulo cónico gira alrededor del eje Z con velocidad angular dφ/dt constante, haciendo un ángulo θ₀ con la vertical. La partícula describirá una trayectoria circular de radio lsinθ₀ perpendicular al eje Z.

Si θ=θ₀=constante, dφ/dt=constante.

${\displaystyle \begin{array}{l}{h}^2={\omega }_0^2\frac{{\sin }^4{\theta }_0}{\cos {\theta }_0}\\ \frac{d\phi }{dt}=\frac{h}{{\sin }^2{\theta }_0}=\frac{{\omega }_0}{\sqrt{\cos {\theta }_0}}=\sqrt{\frac{g}{l\cos {\theta }_0}}\end{array}}$

Supongamos ahora que θ=θ₀+δ(t). Donde δ es una cantidad pequeña frente a θ₀

Para determinar δ(t), en la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}-\frac{h^2}{{\sin }^3\theta }\cos \theta +{\omega }_0^2\sin \theta =0\\ \frac{d^2\theta }{d{t}^2}+{\omega }_0^2\left(-\frac{{\sin }^4{\theta }_0}{\cos {\theta }_0}\frac{\cos \theta }{{\sin }^3\theta }+\sin \theta \right)=0\end{array}}$

aproximamos el término entre paréntesis utilizando Math Symbolic.

>> syms x x0;
>> y=sin(x)-sin(x0)^4*cos(x)/(cos(x0)*sin(x)^3);
>> z=taylor(y,x,x0,'Order',2);
>> simplify(z)
((x - x0)*(3*cos(x0)^2 + 1))/cos(x0)

La ecuación diferencial se transforma en otra mucho más simple

${\displaystyle \frac{d^2\delta }{d{t}^2}+{\omega }_0^2\frac{1+3{\cos }^2{\theta }_0}{\cos {\theta }_0}\delta =0}$

que corresponde a una oscilación con frecuencias angular

${\displaystyle \Omega ={\omega }_0\sqrt{\frac{1+3{\cos }^2{\theta }_0}{\cos {\theta }_0}}}$

En el script anterior cambiamos las líneas

...
th_1=pi/4+5*pi/180; %50°
th_2=pi/4; %45°
....

para obtener mediante integración numérica la trayectoria de la partícula y compararla con la trayectoria que se obtiene al suponer una trayectoria casi circular

R=1; %longitud del péndulo
w0=sqrt(9.8/R); %frecuencia natural de oscilación
h_1=pi/4+5*pi/180; %50°
th_2=pi/4; %45°
W=w0*sqrt((1+3*cos(th_1)^2)/cos(th_1));
w=w0/sqrt(cos(th_1));
% x(1)=th, x(2)=dth/dt,x(3)=phi
t=0:0.01:5;
th=(th_1+th_2)/2+(th_2-th_1)*sin(W*t)/2;
phi=w*t;
xp=R*sin(th).*cos(phi);
yp=R*sin(th).*sin(phi);
zp=R*cos(th);

%esfera
phi=linspace(0,pi,30);
th=linspace(0,2*pi,40);
[phi,th]=meshgrid(phi,th);
x=R*sin(phi).*cos(th);
y=R*sin(phi).*sin(th);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
axis equal

%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
set(gca,'zDir','reverse')
view (-40,20)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en la superficie de una esfera')

Referencias

Hanno Essén, Nicholas Apazidis. Turning points of the spherical pendulum and the golden ratio. Eur. J. Phys. 30 (2009) pp. 427–432