La aplicación de la mecánica de Lagrange da lugar a n ecuaciones diferenciales correspondientes a n coordenadas generalizadas. El símbolo q_i representa una coordenada generalizada (x, θ, φ, etc). Mostraremos la potencia y sencillez de la formulación de Lagrange

Si T es la energía cinética y V la potencial, entonces la lagrangiana L=T-V. La ecuación de Lagrange correspondiente a la coordenada generalizada q_i es

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}=0i=\mathrm{1,2,3...}}$

El punto encima de la letra q, significa derivada con respecto del tiempo

El péndulo simple

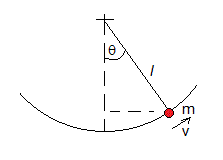
Supongamos que un péndulo simple de masa m y longitud l, se encuentra desviado θ de la posición de equilibrio y lleva una velocidad v=l·(dθ/dt), tangente a la trayectoria circular. La energía cinética de la partícula es

${\displaystyle T=\frac{1}{2}m{v}^2=\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2}$

Estableciedo el nivel cero de la energía potencial en el punto de suspensión, la energía potencial de la partícula es V=-mgcosθ

La lagrangiana L=T-V es

${\displaystyle L=T-V=\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta =\frac{1}{2}m{l}^2{\dot{\theta }}^2+mgl\cos \theta }$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(m{l}^2\dot{\theta }\right)+mgl\sin \theta =0\\ \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta =0\end{array}}$

Péndulo simple que cuelga del techo de un vagón que acelera

Un vagón se mueve con aceleración constante a. Del techo del vagón cuelga un péndulo simple de masa m y longitud l. Vamos aplicar las ecuaciones de Lagrange para determinar la ecuación diferencial del movimiento del péndulo

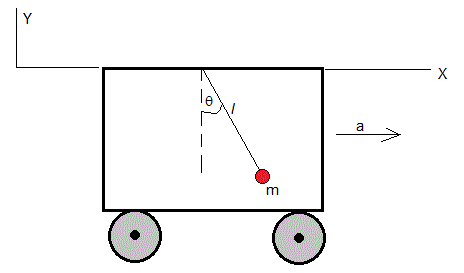
En el instante t, la posición de la masa m es

${\displaystyle \{\begin{array}{l}x=\frac{1}{2}a{t}^2+l\sin \theta \\ y=-l\cos \theta \end{array}}$

Supondremos que el vagón parte del origen en reposo. Derivando obtenemos la velocidad de la partícula

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=at+l\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética de la partícula es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\frac{1}{2}m\left(a^2{t}^2+l^2{\left(\frac{d\theta }{dt}\right)}^2+2l\cos \theta \frac{d\theta }{dt}at\right)}$

La energía potencial de la partícula es V=-mgcosθ

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left(a^2{t}^2+l^2{\left(\frac{d\theta }{dt}\right)}^2+2l\cos \theta \frac{d\theta }{dt}at\right)+mgl\cos \theta \\ L=\frac{1}{2}m\left(a^2{t}^2+l^2{\dot{\theta }}^2+2l\cos \theta ·\dot{\theta }·at\right)+mgl\cos \theta \end{array}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta +\frac{a}{l}\cos \theta =0\end{array}}$

Movimiento de una partícula a lo largo de un aro que gira

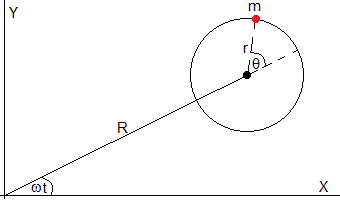
El centro de un aro de radio r se desplaza con velocidad angular ω constante describiendo una trayectoria circular de radio R en el plano horizontal. Una partícula de masa m puede deslizar sin rozamiento a lo largo del aro.

Vamos a calcular la ecuación del movimiento de la partícula. El periodo de las pequeñas oscilaciones alrededor de la posición de equilibrio estable

La posición de la partícula de masa m es

${\displaystyle \{\begin{array}{l}x=R\cos (\omega t)+r\cos (\omega t+\theta )\\ y=R\sin (\omega t)+r\sin (\omega t+\theta )\end{array}}$

Las componentes de su velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=-R\omega \sin (\omega t)-r\left(\omega +\frac{d\theta }{dt}\right)\sin (\omega t+\theta )\\ \frac{dy}{dt}=R\omega \cos (\omega t)+r\left(\omega +\frac{d\theta }{dt}\right)\cos (\omega t+\theta )\end{array}}$

La energía cinética

${\displaystyle E_k=\frac{1}{2}m\left\{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right\}=R^2{\omega }^2+r^2{\left(\omega +\frac{d\theta }{dt}\right)}^2+2Rr\omega \left(\omega +\frac{d\theta }{dt}\right)\cos \theta }$

No hay energía potencial, la lagrangiana es L=mv²/2. La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(2r^2\left(\omega +\frac{d\theta }{dt}\right)+2Rr\omega \cos \theta \right)+2Rr\omega \left(\omega +\frac{d\theta }{dt}\right)\sin \theta =0\\ r\frac{d^2\theta }{d{t}^2}+R{\omega }^2\sin \theta =0\end{array}}$

La misma ecuación que la de un péndulo simple

Como en un péndulo, la posición de equilibrio estable es θ=0, e inestable θ=π. Cuando la amplitud de las oscilaciones es pequeña,

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{R{\omega }^2}{r}\theta =0}$

La ecuación diferencial de un Movimiento Armónico Simple de periodo

${\displaystyle P=\frac{2\pi }{\omega }\sqrt{\frac{r}{R}}}$

Movimiento de los cuerpos celestes

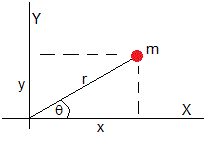
Consideremos un cuerpo celeste de masa m que se mueve alrededor de un centro fijo de fuerzas (por ejemplo el Sol) de masa M, situado en el origen.

La posición del cuerpo en coordenadas polares es

${\displaystyle \{\begin{array}{l}x=r\cos \theta \\ y=r\sin \theta \end{array}}$

La velocidad del cuerpo celeste y su energía cinética es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=\frac{dr}{dt}\cos \theta -r\sin \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=\frac{dr}{dt}\sin \theta +r\cos \theta \frac{d\theta }{dt}\end{array}\\ T=\frac{1}{2}m{v}^2=\frac{1}{2}m\left\{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right\}=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}\end{array}}$

la energía potencial

${\displaystyle V=-G\frac{Mm}{r}}$

La lagrangiana L=T-V es

${\displaystyle L=T-V=\frac{1}{2}m\left({\dot{r}}^2+r^2{\dot{\theta }}^2\right)+G\frac{Mm}{r}}$

La lagrangiana es función de dos coordenadas r y θ. Por tanto, hay dos ecuaciones del movimiento. La primera es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ \frac{d}{dt}\left(m\dot{r}\right)-mr{\dot{\theta }}^2+G\frac{Mm}{r^2}=0\\ \frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2+G\frac{M}{r^2}=0\end{array}}$

La segunda es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(m{r}^2\dot{\theta }\right)=0\\ \frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)=0\end{array}}$

Esta ecuación nos dice que hay una magnitud r²(dθ/dt), momento angular, que se mantiene constante

La máquina de Atwood

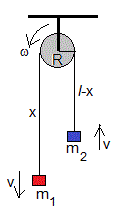
Una máquina de Atwood es un dispositivo consta de una polea de radio R y momento de inercia I, y dos masas m₁ y m₂ que cuelgan de una cuerda que pasa por una polea y se mueven con la misma velocidad v. Si la cuerda no resbala la velocidad angular de rotación de la polea ω=v/R.

La energía cinética del sistema formado por los tres cuerpos es

${\displaystyle T=\frac{1}{2}{m}_1{v}^2+\frac{1}{2}{m}_2{v}^2+\frac{1}{2}I{\omega }^2=\frac{1}{2}\left(m_1+m_2+\frac{I}{R^2}\right){\left(\frac{dx}{dt}\right)}^2}$

Estableciendo el nivel cero de energía potencial en el eje de la polea. La energía potencial del sistema es

${\displaystyle V=-m_{1}gx-m_{2}g(l-x)}$

La lagrangiana L=T-V es

${\displaystyle L=T-V=\frac{1}{2}\left(m_1+m_2+\frac{I}{R^2}\right){\dot{x}}^2+m_{1}gx+m_{2}g(l-x)}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ \frac{d}{dt}\left(\left(m_1+m_2+\frac{I}{R^2}\right)\dot{x}\right)-m_{1}g+m_{2}g=0\\ \left(m_1+m_2+\frac{I}{R^2}\right)\frac{d^{2}x}{d{t}^2}=(m_1-m_2)g\end{array}}$

Una máquina doble de Atwood

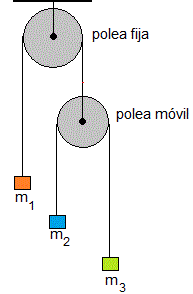
Consideremos el siguiente sistema mecánico formado por los bloques de masas m₁, m₂ y m₃. Los bloques de masas m₂ y m₃ forman una máquina de Atwood pero la polea de masa despreciable no es fija sino móvil. Esta polea forma parte de otra máquina de Atwood con la masa m₁, la polea superior de masa despreciable es fija.

Descripción en términos de fuerzas

Dibujamos los vectores fuerza sobre cada cuerpo y sus aceleraciones

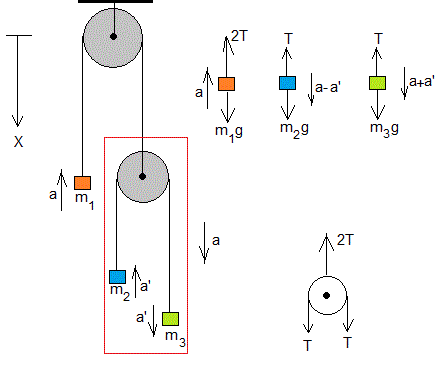
Supongamos que el bloque de masa m₁ asciende con una aceleración a₁=-a, bajo la acción de dos fuerzas 2T y m₁g. Donde 2T es la tensión de las cuerda que une m₁ y la polea móvil a través de la polea fija. La ecuación del movimiento es

2T-m₁g=m₁a

La polea móvil desciende con una aceleración a. Dentro de la caja de color rojo, los bloques de masa m₂ y m₃ se mueven con aceleración a'.

• la aceleración del bloque de masa m₂ será, a₂=a-a'
• la aceleración del bloque de masa m₃ será, a₃=a+a'

La tensión de la cuerda que une los bloques de masas m₂ y m₃ a través de la polea móvil es T.

• La ecuación del movimiento del bloque de masa m₂ será, m₂g-T=m₂(a-a')
• La ecuación del movimiento del bloque de masa m₃ será, m₃g-T=m₃(a+a')

${\displaystyle \{\begin{array}{l}2T-m_{1}g=m_{1}a\\ m_{2}g-T=m_2(a-a\text{'})\\ m_{3}g-T=m_3(a+a\text{'})\end{array}}$

Eliminando la tensión T se obtiene un sistema de dos ecuaciones con dos incógnitas a y a'

${\displaystyle \{\begin{array}{l}(m_1+m_2+m_3)a+(m_3-m_2)a\text{'}=(m_2+m_3-m_1)g\\ (m_3-m_2)a+(m_3+m_2)a\text{'}=(m_3-m_2)g\end{array}}$

La solución de este sistema es

${\displaystyle \begin{array}{l}a=\frac{4m_2{m}_3-m_1{m}_2-m_1{m}_3}{4m_2{m}_3+m_1{m}_2+m_1{m}_3}g\\ a\text{'}=\frac{2m_1(m_3-m_2)}{4m_2{m}_3+m_1{m}_2+m_1{m}_3}g\end{array}}$

Si el eje X apunta hacia abajo, las aceleraciones de los bloques son:

${\displaystyle \begin{array}{l}{a}_1=-a=\frac{-4m_2{m}_3+m_1{m}_2+m_1{m}_3}{4m_2{m}_3+m_1{m}_2+m_1{m}_3}g\\ a_2=a-a\text{'}=\frac{4m_2{m}_3-3m_1{m}_3+m_1{m}_2}{4m_2{m}_3+m_1{m}_2+m_1{m}_3}g\\ a_3=a+a\text{'}=\frac{4m_2{m}_3+m_1{m}_3-3m_1{m}_2}{4m_2{m}_3+m_1{m}_2+m_1{m}_3}g\end{array}}$

Ejemplo

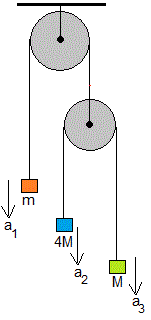
Sea m₁=m, m₂=4M y m₃=M. Las aceleraciones a₁, a₂ y a₃ valen

${\displaystyle a_1=\frac{-16+5\frac{m}{M}}{16+5\frac{m}{M}},a_2=\frac{16+\frac{m}{M}}{16+5\frac{m}{M}},a_3=\frac{16-11\frac{m}{M}}{16+5\frac{m}{M}}}$

Si los tres cuerpos parten del reposo

• el cuerpo 2 de masa 4M no puede seguir en reposo, a₂ es siempre positiva
• el cuerpo 1 de masa m permenecerá en reposo si m/M=16/5
• el cuerpo 3 de masa M permenecerá en reposo si m/M=16/11

Ecuaciones de Lagrange

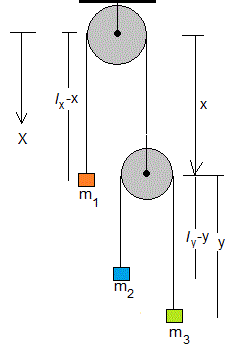
Sea l_x la longitud de la cuerda que pasa a través de la polea superior, y l_y la longitud de la cuerda que pasa por la polea móvil. Tomamos el sentido positivo del eje X hacia abajo. Las posiciones de las partículas son:

x₁=l_x-x
x₂=x+(l_y-y)
x₃=x+y

Las velocidades de las partículas son:

${\displaystyle \begin{array}{l}\frac{d{x}_1}{dt}=-\frac{dx}{dt}\\ \frac{d{x}_2}{dt}=\frac{dx}{dt}-\frac{dy}{dt}\\ \frac{d{x}_3}{dt}=\frac{dx}{dt}+\frac{dy}{dt}\end{array}}$

La energía cinética del sistema de tres masas es

${\displaystyle \begin{array}{l}T=\frac{1}{2}{m}_1{\left(\frac{d{x}_1}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(\frac{d{x}_2}{dt}\right)}^2+\frac{1}{2}{m}_3{\left(\frac{d{x}_3}{dt}\right)}^2=\\ \frac{1}{2}(m_1+m_2+m_3){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}(m_2+m_3){\left(\frac{dy}{dt}\right)}^2+(m_3-m_2)\left(\frac{dx}{dt}\right)\left(\frac{dy}{dt}\right)\end{array}}$

La energía potencial es

${\displaystyle \begin{array}{l}V=-m_{1}g{x}_1-m_{2}g{x}_2-m_{3}g{x}_3=\\ -(m_2+m_3-m_1)gx-(m_3-m_2)gy-m_{1}g{l}_x-m_{2}g{l}_y\end{array}}$

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}(m_1+m_2+m_3){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}(m_2+m_3){\left(\frac{dy}{dt}\right)}^2+(m_3-m_2)\left(\frac{dx}{dt}\right)\left(\frac{dy}{dt}\right)\\ +(m_2+m_3-m_1)gx+(m_3-m_2)gy+m_{1}g{l}_x+m_{2}g{l}_y\end{array}}$

La lagrangiana depende de dos parámetros x e y. La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ \frac{d}{dt}\left((m_1+m_2+m_3)\dot{x}+(m_3-m_2)\dot{y}\right)-(m_2+m_3-m_1)g=0\\ (m_1+m_2+m_3)\frac{d^{2}x}{d{t}^2}+(m_3-m_2)\frac{d^{2}y}{d{t}^2}=(m_2+m_3-m_1)g\end{array}}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial y}=0\\ \frac{d}{dt}\left((m_2+m_3)\dot{y}+(m_3-m_2)\dot{x}\right)-(m_3-m_2)g=0\\ (m_2+m_3)\frac{d^{2}y}{d{t}^2}+(m_3-m_2)\frac{d^{2}x}{d{t}^2}=(m_3-m_2)g\end{array}}$

Se trata de las mismas ecuaciones que hemos obtenido mediante las leyes de Newton con a=d²x/dt² y a'=d²y/dt²

Referencias

David Morin. Chapter 5. The Lagrangian Method. 2002

Physics Challenge for Teachers and Students. M&m&4M. The Physics Teacher. Vol. 57, November 2019, pp. 567.
Solution to the November, 2019 Challenge, M&m&4M. Phys. Teach. 58, A118 (2020)