A la izquierda, una fotografía del péndulo de Foucault para una demostración en una Feria de la Ciencia. El péndulo de Foucault del Museo de las Artes y las Ciencias de Valencia es mucho más largo

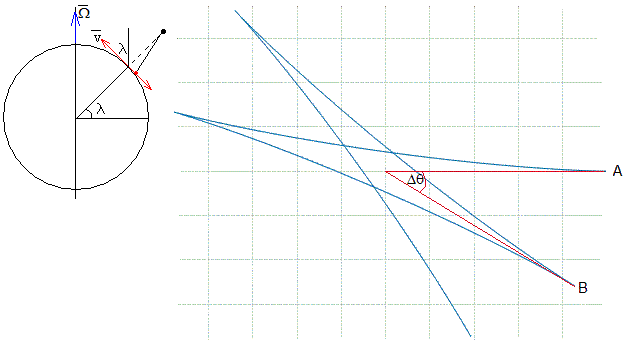
En la figura (más abajo), se muestra el ángulo girado por el plano de oscilación del "péndulo" durante el periodo de una oscilación. El péndulo parte de A y regresa a B, para iniciar una nueva oscilación. El ángulo girado es Δθ =Ω·P. Siendo P=2π/ω_p el periodo de una oscilación

El ángulo girado por el plano de oscilación del péndulo en una hora, es el producto de Δθ por el número de oscilaciones que da el péndulo en una hora.

Δθ·60·60/P=Ω·60·60=15º a la hora

Teniendo en cuenta que la velocidad angular de rotación Ω de la Tierra es de 360º en 24 h.

Para un lugar de latitud λ, el ángulo girado por el plano de oscilación del péndulo en una hora vale 15º·sinλ. La razón estriba en que el vector velocidad angular de rotación $\overrightarrow{\Omega }$ forman un ángulo 90º-λ con la dirección perpendicular al plano local, tal como se ve en la figura. Recuérdese que la aceleración de Coriolis responsable de este fenómeno es el producto vectorial $-2\overrightarrow{\Omega }\times \overrightarrow{v}$

Sabiendo que la latitud de Paris es de aproximadamente 49º, el plano de oscilación del péndulo de Foucault gira a razón de 11.3º cada hora.

Para describir el péndulo de Foucault, se pueden seguir los mismos pasos que para el péndulo esférico, salvo que el ahora está situado en un Sistema de Referencia Local, no inercial.

Sin embargo, el péndulo de Foucault es muy largo y el ángulo de desviación es pequeño por lo que es aplicable la aproximación lineal. En esta aproximación, el péndulo se comporta de forma análoga a una masa unida a un muelle elástico. Este sistema es más sencillo y ya hemos estudiado en una página anterior, el comportamiento de una masa unida a un muelle elástico situado sobre una plataforma que gira con velocidad angular constante

Ecuaciones del movimiento

En la página titulada Movimiento relativo en el Sistema de Referencia Local estudiamos el movimiento de una partícula en el Sistema de Referencia Local, llegando a las siguientes ecuaciones:

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}-2m\Omega \frac{dy}{dt}\cos \alpha -m{\Omega }^2\left(x\cos \alpha +(R+z)\sin \alpha \right)\cos \alpha +\frac{\partial V}{\partial x}=0\\ m\frac{d^{2}y}{d{t}^2}+2m\Omega \left(\frac{dx}{dt}\cos \alpha +\frac{dz}{dt}\sin \alpha \right)-m{\Omega }^{2}y+\frac{\partial V}{\partial y}=0\\ m\frac{d^{2}z}{d{t}^2}-2m\Omega \frac{dy}{dt}\sin \alpha -m{\Omega }^2\left(x\cos \alpha +(R+z)\sin \alpha \right)\sin \alpha +\frac{\partial V}{\partial z}=0\end{array}}$

Consideremos una partícula de masa m unida a uno de los extremos de un muelle elástico de constante k mientras que el otro está sujeto al origen del Sistema de Referencia Local. El muelle está en el plano XY, su energía potencial será

${\displaystyle V(x,y)=\frac{1}{2}k\left(x^2+y^2\right)=\frac{1}{2}m{\omega }^2\left(x^2+y^2\right)}$

La partícula se mueve en el plano XY, con z=0 y dz/dt=0, las ecuaciones del movimiento son ahora

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}\cos \alpha +\left({\omega }^2-{\Omega }^2\cos \alpha \right)x=\frac{1}{2}{\Omega }^{2}R\sin (2\alpha )\\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}\cos \alpha +\left({\omega }^2-{\Omega }^2\right)y=0\end{array}}$

Eliminamos el término constante en la primera ecuación, con un cambio de variable x'=x+c. Resolvemos el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales

${\displaystyle t=0\{\begin{array}{l}\frac{dx}{dt}={\dot{x}}_0\frac{dy}{dt}={\dot{y}}_0\\ x=x_{0}y=y_0\end{array}}$

w=1; %muelle elástico
W=w/10; %velocidad angular de rotación
alfa=pi/6; %posición del observador
x0=[1,0,0,0]; %condiciones iniciales
tspan=[0,50];
% x(1)=x, x(2)=dx/dt,x(3)=y, x(4)=dy/dt
fg=@(t,x)[x(2); 2*W*x(4)*cos(alfa)+(W^2*cos(alfa)-w^2)*x(1); x(4);
 -2*W*x(2)*cos(alfa)+(W^2-w^2)*x(3)];
[t,x]=ode45(fg,tspan,x0);
 
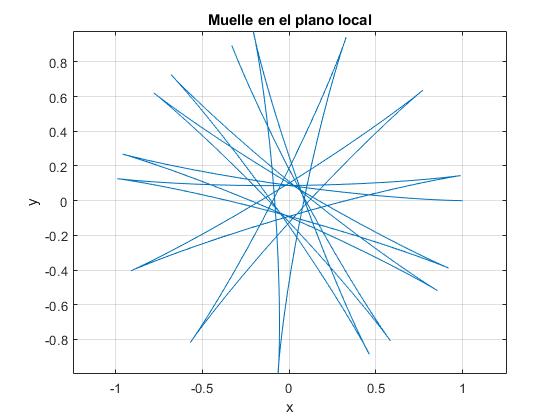
plot(x(:,1),x(:,3))
grid on
axis equal
xlabel('x')
ylabel('y')
title('Muelle en el plano local')

Aproximaciones

Si despreciamos los términos en Ω², el sistema de ecuaciones diferenciales se puede resolver de forma análoga al caso del muelle sobre una plataforma en rotación

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}\cos \alpha +{\omega }^{2}x=0\\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}\cos \alpha +{\omega }^{2}y=0\end{array}}$

Utilizando la notación compleja ξ=x+iy, el sistema de dos ecuaciones diferenciales se transforma en una única ecuación diferencial en ξ

${\displaystyle \frac{d^2\xi }{d{t}^2}+2\Omega i\frac{d\xi }{dt}\cos \alpha +{\omega }^2\xi =0}$

Las raíces de la ecuación característica son

${\displaystyle s^2+2\Omega i\cos \alpha ·s+{\omega }^2=0\{\begin{array}{l}{s}_1=i\left(-\Omega \cos \alpha +\sqrt{{\omega }^2+{\Omega }^2{\cos }^2\alpha }\right)\\ s_2=i\left(-\Omega \cos \alpha -\sqrt{{\omega }^2+{\Omega }^2{\cos }^2\alpha }\right)\end{array}}$

Escribimos las raíces s₁=i(-a+b) y s₂=-i(a+b)

La solución de la ecuación diferencial lineal homogénea es

${\displaystyle \xi =C\exp \left(i(-a+b)t\right)+D\exp \left(-i(a+b)t\right)=\left(C\exp \left(ibt\right)+D\exp \left(-ibt\right)\right)\exp \left(-iat\right)}$

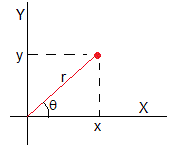
Un número complejo se expresa en forma polar, ξ=x+iy=r·exp(iθ)

Identidicamos θ=-at o bien, θ=-Ωcosα·t. El plano de oscilación del péndulo de Foucault gira con velocidad angular constante Ω·cosα en el sentido de las agujas del reloj, tal como puede verse en la simulación al final de la página

Los coeficientes C y D de la solución de la ecuación diferencial, son números complejos cuya parte real e imaginaria se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}x=x_0\frac{dx}{dt}={\dot{x}}_0\\ y=y_0\frac{dy}{dt}={\dot{y}}_0\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}C=\frac{1}{2}\left(\left(1+\frac{a}{b}\right)x_0+\frac{{\dot{y}}_0}{b}\right)+i\left(\left(1+\frac{a}{b}\right)y_0-\frac{{\dot{x}}_0}{b}\right)\\ D=\frac{1}{2}\left(\left(1-\frac{a}{b}\right)x_0-\frac{{\dot{y}}_0}{b}\right)+i\left(\left(1-\frac{a}{b}\right)y_0+\frac{{\dot{x}}_0}{b}\right)\end{array}}$

Las expresiones de x e y en función del tiempo son:

${\displaystyle \begin{array}{l}x=C_r\cos (-a+b)t+D_r\cos (a+b)t-C_i\sin (-a+b)t+D_i\sin (a+b)t\\ y=C_i\cos (-a+b)t+D_i\cos (a+b)t+C_r\sin (-a+b)t-D_r\sin (a+b)t\end{array}}$

Donde C_r es la parte real del coeficiente C, C_i es la parte imaginaria y lo mismo cabe decir del coeficiente D

alfa=pi/6; %posición
w=1;  %sqrt(k/m)
W=w/10;  %velocidad rotación
a=W*cos(alfa);
b=sqrt(w^2+(W*cos(alfa))^2);
x0=1;   %posición inicial
y0=0;
vx0=0; %velocidad inicial
vy0=0;

%coeficientes
C=((1+a/b)*x0+vy0/b+1i*((1+a/b)*y0-vx0/b))/2;
D=((1-a/b)*x0-vy0/b+1i*((1-a/b)*y0+vx0/b))/2;
x=@(t) real(C)*cos((b-a)*t)+real(D)*cos((a+b)*t)-
imag(C)*sin((b-a)*t)+imag(D)*sin((a+b)*t);
y=@(t) imag(C)*cos((b-a)*t)+imag(D)*cos((b+a)*t)+
real(C)*sin((b-a)*t)-real(D)*sin((b+a)*t);
fplot(x,y,[0,50])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Muelle en el plano local')

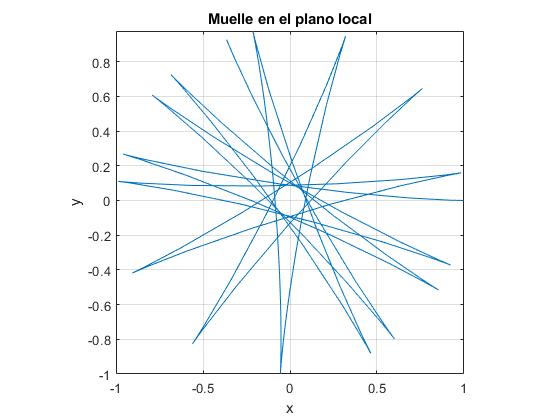
Comparando las dos figuras, vemos que son similares. En la primera hemos incluido términos proporcionales a Ω² y en la segunda los hemos despreciado. En el caso del péndulo de Foaucault de longitud 67 m, la frecuencia ω de oscilación del péndulo y la velocidad angular de rotación Ω de la Tierra son, respectivamente.

${\displaystyle \begin{array}{l}\omega =\sqrt{g/l}=\sqrt{9.8/67}=\text{0}\text{.382}\text{rad/s}\\ \Omega \text{=}\frac{2\pi }{24·60·60}=\text{7}{\text{.27·10}}^{-5}\text{rad/s}\end{array}}$

Lo que justifica la eliminación de los términos proporcionales a Ω² en el sistema de dos ecuaciones diferenciales

En este programa, la trayectoria de la partícula unida a un muelle elástico en el Sistema de Referencia Local, se calcula resolviendo el sistema de dos ecuaciones diferenciales (incluyendo los términos proporcionales a Ω²) por el procedimiento de Runge-Kutta.

Actividades

Especificamos los parámetros del sistema

• La posición del observador, el control titulado Posición α
• La velocidad angular de rotación, el control titulado Rotación Ω
• El cociente ω²=k/m, donde k es la constante del muelle y m la masa de la partícula se ha fijado en ω=1

Especificamos las condiciones iniciales

• La posición inicial x₀ e y₀, en los controles titulados Posición, X y Posición, Y
• La velocidad inicial (dx/dt)₀ e (dy/dt)₀, en los controles titulados Velocidad, X y Velocidad, Y

Si la trayectoria aparece grande o se ve pequeña, se puede reducir o aumentar la escala para ajustarla a la ventana gráfica, en el control titulado Escala

Péndulo en un vehículo que describe una trayectoria circular

Vamos a plantear un problema similar al péndulo de Foucault. Estudiamos el movimiento de un péndulo que cuelga del techo de un vehículo que describe una trayectoria circular de radio R con velocidad constante v=ΩR.

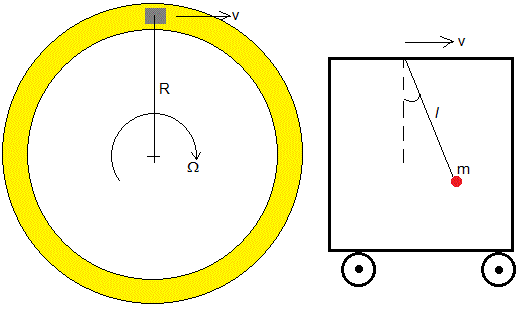
El péndulo consiste en un hilo inextensible de longitud l cuyo extremo libre sujeta una masa puntual m

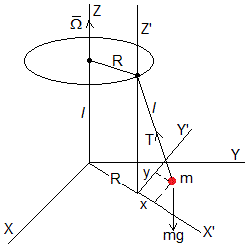
Vamos a estudiar el movimiento del péndulo en el Sistema de Referencia del vehículo X'Y'Z'

En un instante t la posición de la masa puntual respecto a este Sistema de Referencia es (x, y, z)

Las fuerzas sobre la masa puntual son

• El peso, mg
• la tensión del hilo, T

Escribimos la ecuación del movimiento en el Sistema de Referencia en rotación

${\displaystyle m\frac{d^2\overrightarrow{r}}{d{t}^2}=-mg\widehat{k}+\overrightarrow{T}-2m\overrightarrow{\Omega }\times \frac{d\overrightarrow{r}}{dt}-m\overrightarrow{\Omega }\times \left(\overrightarrow{\Omega }\times \overrightarrow{r}\right)}$

Efectuamos los productos vectoriales, calculando las expresiones de la aceleración de Coriolis y centrífuga

${\displaystyle \begin{array}{l}2m\overrightarrow{\Omega }\times \frac{d\overrightarrow{r}}{dt}=2m\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 0& 0& \Omega \\ \frac{dx}{dt}& \frac{dy}{dt}& \frac{dz}{dt}\end{array}\right|=2m\Omega \left(-\frac{dy}{dt}\widehat{i}+\frac{dx}{dt}\widehat{j}\right)\\ \overrightarrow{\Omega }\times \overrightarrow{r}=\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 0& 0& \Omega \\ R+x& y& z\end{array}\right|=\Omega \left(-y\widehat{i}+\left(R+x\right)\widehat{j}\right)\\ m\overrightarrow{\Omega }\times \left(\overrightarrow{\Omega }\times \overrightarrow{r}\right)=m\Omega \left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 0& 0& \Omega \\ -y& \left(R+x\right)& z\end{array}\right|=-m{\Omega }^2\left(\left(R+x\right)\widehat{i}+y\widehat{j}\right)\end{array}}$

El resultado es un sistema de tres ecuaciones diferenciales

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}x}{d{t}^2}\widehat{i}+\frac{d^{2}y}{d{t}^2}\widehat{j}+\frac{d^{2}z}{d{t}^2}\widehat{k}\right)=-mg\widehat{k}+\left(T_x\widehat{i}+T_y\widehat{j}+T_z\widehat{k}\right)-2m\Omega \left(-\frac{dy}{dt}\widehat{i}+\frac{dx}{dt}\widehat{j}\right)+m{\Omega }^2\left(\left(R+x\right)\widehat{i}+y\widehat{j}\right)\\ \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{x}{l}\frac{T}{m}+2\Omega \frac{dy}{dt}+{\Omega }^2\left(R+x\right)\\ \frac{d^{2}y}{d{t}^2}=-\frac{y}{l}\frac{T}{m}-2\Omega \frac{dx}{dt}+{\Omega }^{2}y\\ \frac{d^{2}z}{d{t}^2}=\frac{z}{l}\frac{T}{m}-g\end{array}\end{array}}$

Si la longitud l del péndulo es grande, para amplitudes pequeñas, z≈l, dz/dt≈0, d²z/dt²≈0. La tensión de la cuerda T≈mg, es casi igual al peso

Tenemos que resolver el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\left({\Omega }^2-\frac{g}{l}\right)x+2\Omega \frac{dy}{dt}+{\Omega }^{2}R\\ \frac{d^{2}y}{d{t}^2}=\left({\Omega }^2-\frac{g}{l}\right)y-2\Omega \frac{dx}{dt}\end{array}}$

Con la sustitución u=x+iy,(i es la unidad imaginaria) se transforma en una única ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{t}^2}=\left({\Omega }^2-\frac{g}{l}\right)u-2\Omega i\frac{du}{dt}+{\Omega }^{2}R\\ \frac{d^{2}u}{d{t}^2}+2\Omega i\frac{du}{dt}-\left({\Omega }^2-\frac{g}{l}\right)u={\Omega }^{2}R\end{array}}$

Buscamos la solución particular que es una constante u_p=c, introduciéndola en la ecuación diferencial

${\displaystyle \begin{array}{l}-\left({\Omega }^2-\frac{g}{l}\right)c={\Omega }^{2}R\\ c=\frac{{\Omega }^{2}R}{\frac{g}{l}-{\Omega }^2}\end{array}}$

Buscamos la solución de la homogénea, determinando las raíces de la ecuación característica

${\displaystyle \begin{array}{l}{s}^2+2\Omega is-\left({\Omega }^2-\frac{g}{l}\right)=0\\ s=\frac{-2\Omega i\pm \sqrt{-4{\Omega }^2+4\left({\Omega }^2-\frac{g}{l}\right)}}{2}=\left(-\Omega \pm \frac{g}{l}\right)i\\ u_h=c_1\exp \left(i\left(-\Omega +\frac{g}{l}\right)t\right)+c_2\exp \left(-i\left(\Omega +\frac{g}{l}\right)t\right)\end{array}}$

La solución completa es

${\displaystyle \begin{array}{l}u=u_h+u_p=c_1\exp \left(i\left(-\Omega +\sqrt{\frac{g}{l}}\right)t\right)+c_2\exp \left(-i\left(\Omega +\sqrt{\frac{g}{l}}\right)t\right)+\frac{{\Omega }^{2}R}{\frac{g}{l}-{\Omega }^2}\\ \frac{du}{dt}=i\left(-\Omega +\sqrt{\frac{g}{l}}\right)c_1\exp \left(i\left(-\Omega +\sqrt{\frac{g}{l}}\right)t\right)-i\left(\Omega +\sqrt{\frac{g}{l}}\right)c_2\exp \left(-i\left(\Omega +\sqrt{\frac{g}{l}}\right)t\right)\end{array}}$

El péndulo se separa x₀ de la posición de equilibrio a lo largo del eje X' y se suelta. Las condiciones iniciales son

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}x=x_0\\ y=0\end{array}\{\begin{array}{l}\frac{dx}{dt}=0\\ \frac{dy}{dt}=0\end{array}\\ \{\begin{array}{l}{x}_0=c_1+c_2+\frac{{\Omega }^{2}R}{\frac{g}{l}-{\Omega }^2}\\ 0=c_1\left(-\Omega +\sqrt{\frac{g}{l}}\right)-c_2\left(\Omega +\sqrt{\frac{g}{l}}\right)\end{array}\\ c_1=\frac{x_0\left(\frac{g}{l}-{\Omega }^2\right)-{\Omega }^{2}R}{2\sqrt{\frac{g}{l}}\left(-\Omega +\sqrt{\frac{g}{l}}\right)},c_2=\frac{x_0\left(\frac{g}{l}-{\Omega }^2\right)-{\Omega }^{2}R}{2\sqrt{\frac{g}{l}}\left(\Omega +\sqrt{\frac{g}{l}}\right)}\end{array}}$

Descomponemos la solución

${\displaystyle \{\begin{array}{l}x=\frac{x_0\left(\frac{g}{l}-{\Omega }^2\right)-{\Omega }^{2}R}{2\sqrt{\frac{g}{l}}}\left\{\frac{\cos \left(\left(-\Omega +\sqrt{\frac{g}{l}}\right)t\right)}{-\Omega +\sqrt{\frac{g}{l}}}+\frac{\cos \left(\left(\Omega +\sqrt{\frac{g}{l}}\right)t\right)}{\Omega +\sqrt{\frac{g}{l}}}\right\}+\frac{{\Omega }^{2}R}{\frac{g}{l}-{\Omega }^2}\\ y=\frac{x_0\left(\frac{g}{l}-{\Omega }^2\right)-{\Omega }^{2}R}{2\sqrt{\frac{g}{l}}}\left\{\frac{\sin \left(\left(-\Omega +\sqrt{\frac{g}{l}}\right)t\right)}{-\Omega +\sqrt{\frac{g}{l}}}-\frac{\sin \left(\left(\Omega +\sqrt{\frac{g}{l}}\right)t\right)}{\Omega +\sqrt{\frac{g}{l}}}\right\}\end{array}}$

Utilizamos las fórmulas, cos(a+b)=cosa·cosb-sina·sinb, sin(a+b)=sina·cosb+sinb·cosa

${\displaystyle \{\begin{array}{l}x=\left(x_0+\frac{{\Omega }^{2}R}{{\Omega }^2-\frac{g}{l}}\right)\left\{\Omega \sqrt{\frac{l}{g}}\sin \left(\Omega t\right)\sin \left(\sqrt{\frac{g}{l}}t\right)+\cos \left(\Omega t\right)\cos \left(\sqrt{\frac{g}{l}}t\right)\right\}+\frac{{\Omega }^{2}R}{\frac{g}{l}-{\Omega }^2}\\ y=\left(x_0+\frac{{\Omega }^{2}R}{{\Omega }^2-\frac{g}{l}}\right)\left\{\Omega \sqrt{\frac{l}{g}}\cos \left(\Omega t\right)\sin \left(\sqrt{\frac{g}{l}}t\right)-\sin \left(\Omega t\right)\cos \left(\sqrt{\frac{g}{l}}t\right)\right\}\end{array}}$

Aproximaciones: si ${\Omega }^2<<\frac{g}{l},\Omega \sqrt{\frac{l}{g}}<<1$, entonces

${\displaystyle \{\begin{array}{l}x=x_0\cos \left(\Omega t\right)\cos \left(\sqrt{\frac{g}{l}}t\right)\\ y=-x_0\sin \left(\Omega t\right)\cos \left(\sqrt{\frac{g}{l}}t\right)\end{array}}$

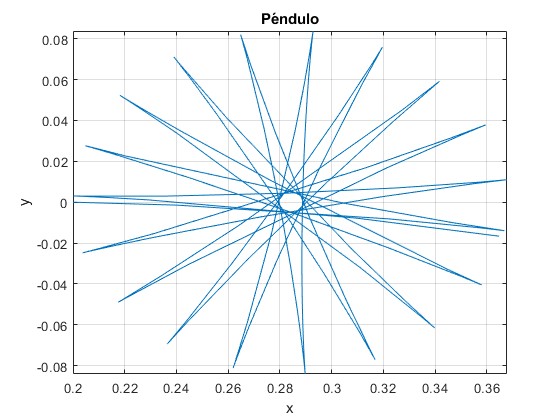
Ejemplo

• Longitud del péndulo, l=1 m
• Desviación inicial del péndulo, x₀=0.2 m
• Velocidad angular del vehículo, Ω=1/6 rad/s
• Radio de la trayectoria circular, R=100 m

La velocidad del vehículo es, v=ΩR=50/3 m/s=60 km/h

l=1; %longitud del péndulo
w=1/6; %velocidad angular
R=100; %radio de la trayectoria circular
x0=0.2; %desviación inicial del péndulo
x=@(t) (x0+w^2*R/(w^2-9.8/l))*(w*sqrt(l/9.8)*sin(w*t).*sin(sqrt(9.8/l)*t)+
cos(w*t).*cos(sqrt(9.8/l)*t))+w^2*R/(9.8/l-w^2);
y=@(t) (x0+w^2*R/(w^2-9.8/l))*(w*sqrt(l/9.8)*cos(w*t).*sin(sqrt(9.8/l)*t)-
sin(w*t).*cos(sqrt(9.8/l)*t));
fplot(x,y,[0,20])
grid on
xlabel('x')
ylabel('y')
title('Péndulo')

Referencias

Walter Greiner. Classical Mechanics. Systems of Particles and Hamiltonian Dynamics. Springer (1992), pp. 30-34