La parábola de seguridad

La parábola de seguridad.

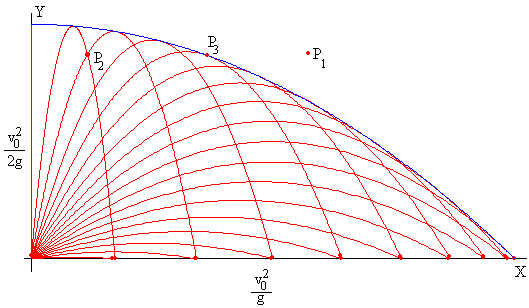
En el programa interactivo al final de la página, se trazan las trayectorias de proyectiles disparados con la misma velocidad inicial v₀ pero con los siguientes ángulos de tiro θ : 10º, 20º, 30º, 40º, 45º, 50º, 60º, 70º, 80º, 90º.

Las ecuaciones del movimiento de los proyectiles y la ecuación de la trayectoria son

$\begin{array}{l} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ y = \tan θ \cdot x - \frac{g x^{2}}{2 v_{0}^{2} \cos^{2} θ} \end{array}$

Hay varias formas de obtener la ecuación de la parábola de seguridad

Parábola que pasa por dos puntos

El alcance horizontal de cada uno de los proyectiles se obtiene para y=0.

$x_{\max} = \frac{v_{0}^{2} sin (2 θ)}{g}$

Su valor máximo se obtiene para θ =45º, teniendo el mismo valor para θ =45+α , que para θ =45-α . Por ejemplo, tienen el mismo alcance los proyectiles disparados con ángulos de tiro de 30º y 60º, ya que sin(2·30)=sin(2·60).

La altura máxima que alcanza un proyectil se obtiene con v_y=0.

$y_{\max} = \frac{v_{0}^{2} {sin}^{2} θ}{2 g}$

Su valor máximo se obtiene para el ángulo de disparo θ =90º.

La envolvente de todas las trayectorias descritas por los proyectiles cuyo ángulo de disparo está comprendido entre 0 y 180º se denomina parábola de seguridad.

Se trata de la parábola simétrica respecto del eje Y de ecuación y=-ax²+b que pasa por los puntos (x=v₀²/g, y=0), y (x=0, y=v₀²/(2g)) tal como se ve en la figura.

La ecuación de dicha parábola es

$y = - \frac{1}{2} \frac{g}{v_{0}^{2}} x^{2} + \frac{1}{2} \frac{v_{0}^{2}}{g}$

Discriminante nulo de la ecuación de segundo grado

Las ecuaciones paramétricas de la trayectoria son

$\begin{array}{l} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

Eliminado el tiempo t, obtenemos la ecuación de la trayectoria

$y = x \tan θ - \frac{g x^{2}}{2 v_{0}^{2} \cos^{2} θ}$

Esta ecuación se puede escribir de forma alternativa

$\tan^{2} θ - \frac{2 v_{0}^{2}}{g x} \tan θ + (1 + \frac{2 v_{0}^{2} y}{g x^{2}}) = 0$

Consideremos un punto arbitrario P del plano. Sustituimos las coordenadas (x, y) del punto en la ecuación de la trayectoria y puede ocurrir

Que la ecuación de segundo grado en tanθ no tenga raíces reales. El punto P₁ no podría ser un punto de impacto para un proyectil disparado con velocidad inicial v₀.
Que la ecuación de segundo grado tenga dos raíces reales, lo que implicará que el punto P₂ es accesible, y que hay dos ángulos de tiro θ₁ y θ₂ que dan en el blanco P₂. En la figura, vemos que cualquier punto en el interior de la envolvente es alcanzado por dos trayectorias.
Cuando la raíz de la ecuación de segundo grado es doble θ₁=θ₂. Como vemos en la figura, solo hay una trayectoria que pasa por un punto P₃ dado de la envolvente.

Para que las raíces sean iguales, se tiene que cumplir que el discriminante b²-4ac de la ecuación de segundo grado ax²+bx+c=0 sea nulo.

${(\frac{2 v_{0}^{2}}{g x})}^{2} - 4 (1 + \frac{2 v_{0}^{2} y}{g x^{2}}) = 0 y = - \frac{g}{2 v_{0}^{2}} x^{2} + \frac{v_{0}^{2}}{2 g}$

Esta es la ecuación de la envolvente que hemos obtenido anteriormente.

Ecuación de la envolvente

La ecuación de la trayectoria depende del ángulo θ con el que se dispara el proyectil. f(x, y, θ)=0

$y = x \tan θ - \frac{g x^{2}}{2 v_{0}^{2}} (1 + \tan^{2} θ)$

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a θ o bien, respecto a tanθ e igualando a cero.

$\begin{array}{l} \frac{\partial f}{\partial θ} = 0 \\ 1 - \frac{g x}{v_{0}^{2}} \tan θ = 0 \tan θ = \frac{v_{0}^{2}}{g x} \end{array}$

Combinamos esta ecuación con la de la trayectoria para eliminar el ángulo θ. Es decir, introducimos la expresión de tanθ en la ecuación de la trayectoria, para obtener la ecuación de la envolvente

$y = - \frac{g}{2 v_{0}^{2}} x^{2} + \frac{v_{0}^{2}}{2 g}$

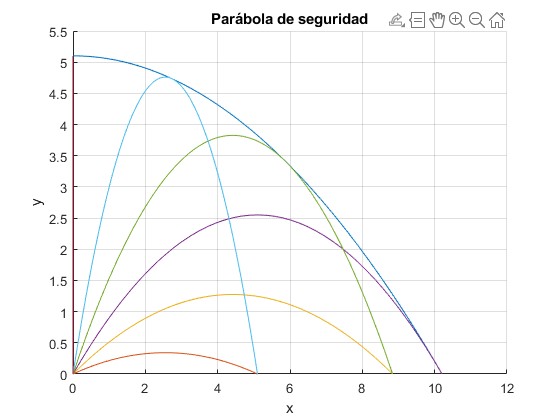
Representamos la parábola de seguridad para los proyectiles disparados con velocidad v₀=10 m/s. Representamos las trayectorias de los proyectiles disparados con ángulos de tiro: 15°, 30°, 45°, 60°, 75°, 90°

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad
hold on
fplot(@(x) -g*x.^2/(2*v0^2)+v0^2/(2*g),[0,v0^2/g])
for th=(15:15:90)*pi/180
      fplot(@(x) x*tan(th)-g*x.^2/(2*v0^2*cos(th)^2), [0,v0^2*sin(2*th)/g])
end
hold off
ylim([0,5.5])
grid on
xlabel('x')
ylabel('y')
title('Parábola de seguridad')

Actividades

Se introduce la velocidad inicial de los proyectiles en el control titulado Velocidad inicial.

Se pulsa el botón titulado Nuevo

Se representa las trayectorias que siguen los proyectiles disparados con ángulo de tiro θ : 10º, 20º, 30º, 40º, 45º, 50º, 60º, 70º, 80º, 90º y la envolvente o parábola de seguridad

En la parte superior derecha se muestra el alcance de cada uno de los proyectiles.

El lector puede calcular, el alcance, la altura máxima y el tiempo de vuelo de un proyectil para algunos de los ángulos de tiro especificados y en especial, el que corresponde a 45º y comparar sus resultados con los proporcionados por el programa interactivo.

Velocidad inicial

Ejemplo

Supongamos que una ametralladora antiaérea situada en el origen, dispara proyectiles con velocidad v₀ y un avión vuela a una altura h.

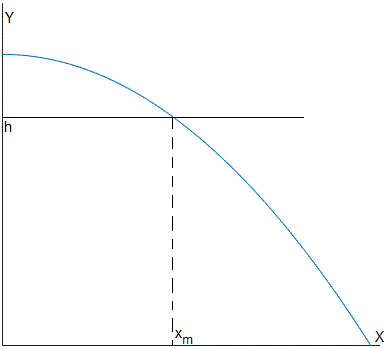
El avión solamente puede ser derribado en el intervalo (0,x_m). En la ecuación de la parábola de seguridad ponemos y=h y despejamos x

$\begin{array}{l} h = - \frac{1}{2} \frac{g}{v_{0}^{2}} x_{m}^{2} + \frac{1}{2} \frac{v_{0}^{2}}{g} \\ x_{m}^{2} = \frac{2 v_{0}^{2}}{g} (\frac{1}{2} \frac{v_{0}^{2}}{g} - h) \end{array}$

La altura máxima del proyectil ha de ser mayor que h. Para un tiro vertical, θ=90°

$\begin{array}{l} {\begin{cases} v = v_{0} - g t \\ h = v_{0} t - \frac{1}{2} g t^{2} \end{cases} \\ v = 0, h_{m á x} = \frac{1}{2} \frac{v_{0}^{2}}{g} \end{array}$

La segunda condición para que el avión pueda ser derribado es que la velocidad de disparo sea suficientemente grande

$v_{0} > \sqrt{2 g h}$

Dada la velocidad de disparo v₀, calculamos el ángulo de tiro θ que hace que el proyectil alcance la altura h.

$\begin{array}{l} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ v_{y} = 0, y = h \\ \sin^{2} θ_{1} = \frac{2 g h}{v_{0}} \end{array}$

Los proyectiles que se disparan con un ángulo de tiro menor que θ₁ no alcanzan la línea altura h. Por tanto, la otra condición es que el ángulo de tiro θ>θ₁

Calculamos el ángulo de tiro θ_m que hace que la trayectoria pase por la posición extrema (x_m, h). Partimos de la ecuación de la trayectoria con y=h y x=x_m, despejamos el ángulo de tiro θ

$\begin{array}{l} h = x_{m} \tan θ - \frac{g x_{m}^{2}}{2 v_{0}^{2} \cos^{2} θ} \\ h = - \frac{g x_{m}^{2}}{2 v_{0}^{2}} (1 + \tan^{2} θ) \\ \frac{g x_{m}^{2}}{2 v_{0}^{2}} \tan^{2} θ - x_{m} \tan θ + h + \frac{g x_{m}^{2}}{2 v_{0}^{2}} = 0 \end{array}$

El discriminante es nulo, solamente hay una raíz

$\tan θ_{m} = \frac{v_{0}^{2}}{g x_{m}} = \frac{v_{0}}{\sqrt{v_{0}^{2} - 2 g h}}$

Representamos la parábola de seguridad para proyectiles disparados con velocidad v₀=10 m/s y la línea horizontal de altura h=3 m, la trayectoria del avión.

Representamos las trayectorias de ángulos de tiro: θ_m=57.3°, tangente a la parábola de seguridad en el punto (6.55,3); θ₁=50.1° tangente a la línea horizontal; θ=70° y 45°

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad
h=3; %altura
hold on
fplot(@(x) -g*x.^2/(2*v0^2)+v0^2/(2*g),[0,v0^2/g])
th_m=atan(v0/sqrt(v0^2-2*g*h));
xm=v0*sqrt(2*(v0^2/(2*g)-h)/g);
line([0,xm],[h,h],'lineStyle','--')
line([xm,xm],[0,h],'lineStyle','--')
fplot(@(x) x*tan(th_m)-g*x.^2/(2*v0^2*cos(th_m)^2), [0,v0^2*sin(2*th_m)/g])
th_1=asin(sqrt(2*g*h)/v0); %tangente a la línea horiontal de altura h
fplot(@(x) x*tan(th_1)-g*x.^2/(2*v0^2*cos(th_1)^2), [0,v0^2*sin(2*th_1)/g])
th=70*pi/180;
fplot(@(x) x*tan(th)-g*x.^2/(2*v0^2*cos(th)^2), [0,v0^2*sin(2*th)/g])
th=45*pi/180;
fplot(@(x) x*tan(th)-g*x.^2/(2*v0^2*cos(th)^2), [0,v0^2*sin(2*th)/g])

hold off
grid on
xlabel('x')
xlim([0,10.5])
ylabel('y')
title('Parábola de seguridad')

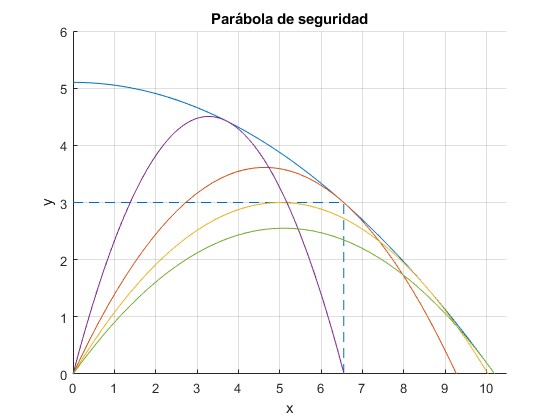
>> th_m*180/pi
ans =   57.3047
>> th_1*180/pi
ans =   50.0684
>> xm
xm =    6.5497

Una valla de protectora

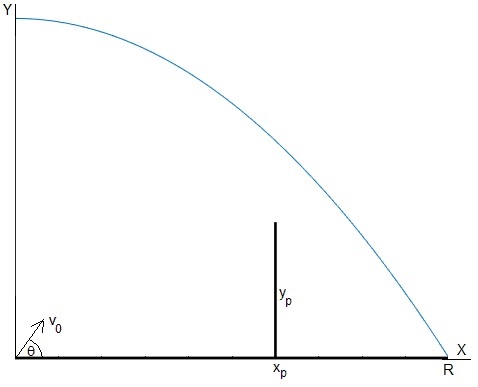
Supongamos una región unidimensional de longitud R. Un cañón situado en el origen dispara proyectiles con velocidad constante v₀ tal que el alcance máximo $R = v_{0}^{2} / g$ , haciendo un ángulo 0<θ<90° de forma aleatoria. Los habitantes de esta región están amenazados, por lo que deciden levantar una valla de seguridad de altura y_p en la posición x_p.

Ahora bien, supondremos que la altura y_p de la valla impenetrable por los proyectiles es menor que la ordenada de la parábola de seguridad en la posición x_p, tal como se muestra en la figura.

La ecuación de la parábola de seguridad es

$y = \frac{1}{2} \frac{v_{0}^{2}}{g} - \frac{1}{2} \frac{g}{v_{0}^{2}} x^{2} = \frac{1}{2} R (1 - \frac{x^{2}}{R^{2}})$

La ordenada y en la posición x_p de la pared es

$y = \frac{1}{2} R (1 - \frac{x_{p}^{2}}{R^{2}})$

Determinamos las trayectorias de las dos parábolas que pasan por el punto (x_p, y_p)

$\begin{array}{l} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ y = \tan θ \cdot x - \frac{1}{2} \frac{g}{v_{0}^{2}} \frac{x^{2}}{\cos^{2} θ} = \tan θ \cdot x - \frac{1}{2} \frac{g x^{2}}{v_{0}^{2}} (1 + \tan^{2} θ) \end{array}$

Dada la posición del blanco, determinamos los dos ángulos de tiro, θ₁ y θ₂ resolviendo la ecuación de segundo grado en tanθ

$\begin{array}{l} \tan^{2} θ - 2 \frac{v_{0}^{2}}{g x_{p}} \tan θ + \frac{2 v_{0}^{2}}{g x_{p}^{2}} y_{p} + 1 = 0 \\ \tan^{2} θ - 2 \frac{R}{x_{p}} \tan θ + \frac{2 R}{x_{p}^{2}} y_{p} + 1 = 0 \\ \tan θ_{1} = \frac{R - \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}}{x_{p}}, \tan θ_{2} = \frac{R + \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}}{x_{p}} \end{array}$

Se obtienen raíces reales si el discriminante es positivo

$y_{p} < \frac{1}{2} R (1 - \frac{x_{p}^{2}}{R^{2}})$

es decir, el extremo de la pared vertical (x_p, y_p) está dentro de la parábola de seguridad

Los alcances x₁ y x₂ de los proyectiles disparados con ángulos θ₁ y θ₂ son

$\begin{array}{l} x_{1} = \frac{v_{0}^{2}}{g} \sin (2 θ_{1}) = 2 R \frac{\tan θ_{1}}{1 + \tan^{2} θ_{1}} = \frac{R - \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}}{(R - y_{p}) - \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}} x_{p} = \frac{x_{p}^{2} + y_{p} (R + \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}})}{x_{p}^{2} + y_{p}^{2}} x_{p} \\ x_{2} = \frac{v_{0}^{2}}{g} \sin (2 θ_{2}) = 2 R \frac{\tan θ_{2}}{1 + \tan^{2} θ_{2}} = \frac{R + \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}}{(R - y_{p}) + \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}}} x_{p} = \frac{x_{p}^{2} + y_{p} (R - \sqrt{R^{2} - x_{p}^{2} - 2 R y_{p}})}{x_{p}^{2} + y_{p}^{2}} x_{p} \end{array}$

Supongamos que la región tiene una longitud R=1000 m, que corresponde al alcance máximo. La velocidad de disparo es por tanto, v₀=98.9949 m/s.

Pueden ocurrir dos casos:

θ₁<45º<θ₂

Situamos la pared de altura y_p=200 m en la posición x_p=500 m

Calculamos los ángulos de tiro θ₁ y θ₂ de las dos trayectorias que pasan por la la posición (x_p, y_p) y sus alcances x₁ y x₂, respectivos

R=1000; %alcance máximo
v0=sqrt(9.8*R); %velocidad de disparo
hold on
fplot(@(x) R*(1-x.^2/R^2)/2, [0,R]) %parábola de seguridad
xp=500; %pared
yp=200;
line([xp,xp],[0,yp],'lineWidth',2, 'color','k') 
x1=(xp^2+yp*(R+sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2); %alcance
x2=(xp^2+yp*(R-sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2);
dis=sqrt((v0^2/(9.8*xp))^2-1-2*v0^2*yp/(9.8*xp^2)); 
th_1=atan(v0^2/(9.8*xp)-dis); %ángulos de tiro
th_2=atan(v0^2/(9.8*xp)+dis);
line([xp,x2],[0,0],'lineWidth',3, 'color','b') %suelo
line([x2,R],[0,0],'lineWidth',3, 'color','r')
line([0,xp],[0,0],'lineWidth',3, 'color','r')

for ang=linspace(th_1,th_2,10)
    fplot(@(x) tan(ang)*x-4.9*x.^2/(v0*cos(ang))^2, [0,v0^2*sin(2*ang)/9.8])
end   
hold off
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Intervalo de seguridad')

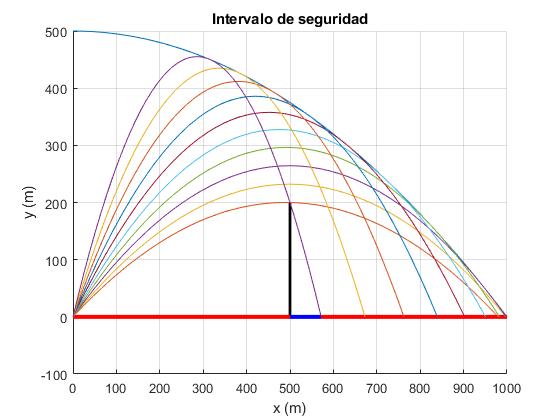
>> th_1*180/pi, th_2*180/pi
ans =   39.2414
ans =   72.5600
>> x1,x2
x1 =  979.8648
x2 =  571.8593

Como apreciamos en la figura, el intervalo de seguridad (en color azul) está comprendido entre (x_p y x₂) que es el alcance correspondiente al ángulo de tiro mayor θ₂=72.56°

Los puntos del intervalo (0, x_p) son alcanzados por proyectiles disparados con ángulos θ en el intervalo (0, θ_p) tal que $x_{p} = R \sin (2 θ_{p})$ y también, por los proyectiles disparados con ángulos θ en el intervalo complementario (π/2-θ_p, π/2)

θ₁, θ₂>45°

Situamos la pared de altura y_p=400 m en la posición x_p=300 m

Calculamos los ángulos de tiro θ₁ y θ₂ de las dos trayectorias que pasan por la la posición (x_p, y_p) y sus alcances x₁ y x₂, respectivos

R=1000; %alcance máximo
v0=sqrt(9.8*R); %velocidad de disparo
hold on
fplot(@(x) R*(1-x.^2/R^2)/2, [0,R]) %parábola de seguridad
xp=300; %pared
yp=400;
line([xp,xp],[0,yp],'lineWidth',2, 'color','k')
x1=(xp^2+yp*(R+sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2); %alcance
x2=(xp^2+yp*(R-sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2);
dis=sqrt((v0^2/(9.8*xp))^2-1-2*v0^2*yp/(9.8*xp^2)); 
th_1=atan(v0^2/(9.8*xp)-dis); %ángulos de tiro
th_2=atan(v0^2/(9.8*xp)+dis);
line([xp,x2],[0,0],'lineWidth',3, 'color','b') %suelo
line([x1,R],[0,0],'lineWidth',3, 'color','b')
line([x2,x1],[0,0],'lineWidth',3, 'color','r')
line([0,xp],[0,0],'lineWidth',3, 'color','r')

for ang=linspace(th_1,th_2,5)
    fplot(@(x) tan(ang)*x-4.9*x.^2/(v0*cos(ang))^2, [0,v0^2*sin(2*ang)/9.8])
end   
hold off
ylim([0,v0^2/(2*9.8)])
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Intervalo de seguridad')

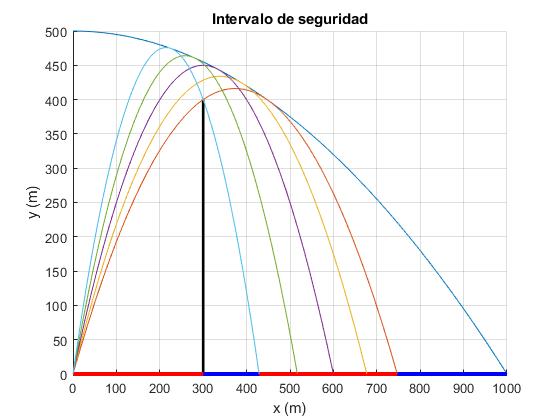
>> th_1*180/pi, th_2*180/pi
ans =   65.8259
ans =   77.3042
>> x1,x2
x1 =  747.1980
x2 =  428.8020

Como apreciamos en la figura, hay dos intervalos de seguridad (en color azul) el primero es (x_p, x₂) que es el alcance correspondiente al ángulo de tiro mayor θ₂=77.30° y el segundo es (x₁, R) que es el alcance correspondiente al ángulo de tiro menor θ₁=65.83°

Incrementamos el intervalo derecho de seguridad con paredes más altas y más cerca del origen

R=1000; %alcance máximo
v0=sqrt(9.8*R); %velocidad de disparo
%parábola de seguriad
hold on
fplot(@(x) R*(1-x.^2/R^2)/2, [0,R]) %parábola de seguridad
xp=100; %pared
yp=400;
line([xp,xp],[0,yp],'lineWidth',2, 'color','k') %pared
x1=(xp^2+yp*(R+sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2);
x2=(xp^2+yp*(R-sqrt(R^2-xp^2-2*R*yp)))*xp/(xp^2+yp^2);
dis=sqrt((v0^2/(9.8*xp))^2-1-2*v0^2*yp/(9.8*xp^2)); 
th_1=atan(v0^2/(9.8*xp)-dis); %ángulos
th_2=atan(v0^2/(9.8*xp)+dis);
line([xp,x2],[0,0],'lineWidth',3, 'color','b')
line([x1,R],[0,0],'lineWidth',3, 'color','b')
line([x2,x1],[0,0],'lineWidth',3, 'color','r')
line([0,xp],[0,0],'lineWidth',3, 'color','r')

for ang=linspace(th_1,th_2,5)
    fplot(@(x) tan(ang)*x-4.9*x.^2/(v0*cos(ang))^2, [0,v0^2*sin(2*ang)/9.8])
end   
hold off
ylim([0,v0^2/(2*9.8)])
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Intervalo de seguridad')

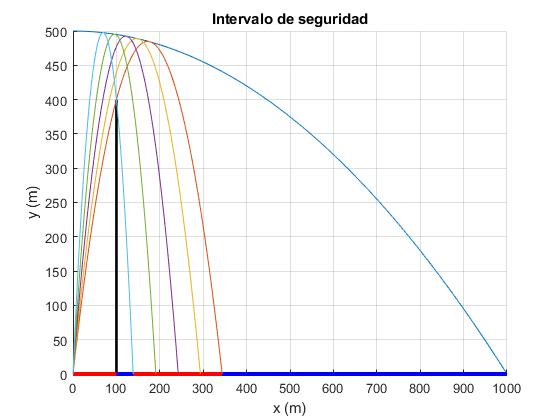
>> th_1*180/pi,th_2*180/pi
ans =   79.9476
ans =   86.0162
>> x1,x2
x1 =  343.7388
x2 =  138.6141

Referencias

Donnelly D. The parabolic envelope of constant initial speed trajectories. Am. J. Phys. 60 (12) December 1992, pp. 1149-1150

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Example 27, pp. 23-24

O. Faella, R. De Luca Living under attack in a one-dimensional virtual world. Revista Brasileira de Ensino de Física, v. 37, n. 3, 3304 (2015). https://www.scielo.br/j/rbef/i/2015.v37n3/