Movimiento de un imán en un tubo metálico vertical

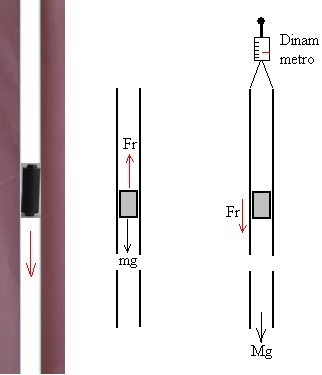
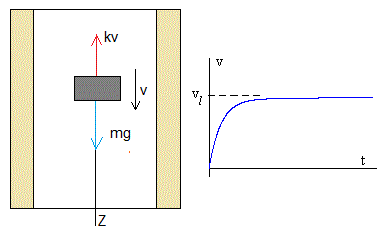
Las fuerzas sobre el imán cuando se mueve a través del tubo son:

• El peso mg, de 54 g
• La fuerza magnética F_r hacia arriba

Por la tercera ley de Newton, la fuerza que ejerce el imán sobre el tubo es F_r hacia abajo

El tubo cuelga de un dinamómetro. El dinamómetro marca Mg+ F_r, donde Mg es el peso del tubo vacío

En esta página, vamos a mostrar que la ecuación que describe el movimiento de caída del imán en un tubo metálico vertical es

${\displaystyle m\frac{dv}{dt}=mg-kv}$

La constante de proporcionalidad k depende del cuadrado del momento magnético del imán y de otros factores como el diámetro interior del tubo, espesor, su conductividad, etc.

Descripción cualitativa

Supongamos que un imán cilíndrico desciende con su polo Sur (color azul) delante y el polo Norte (de color rojo) detrás. En un imán las líneas del campo magnético salen del polo Norte y entran en el polo Sur.

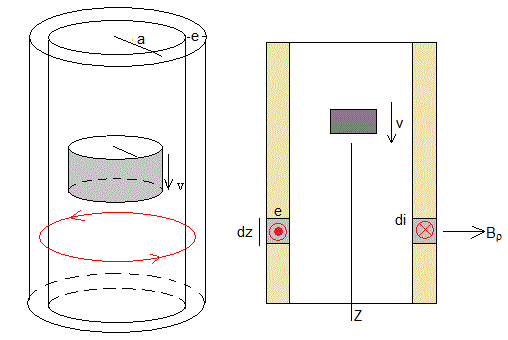
En la figura, se ilustra la aplicación de la ley de Lenz para explicar el origen de la fuerza retardadora sobre el imán en términos de las corrientes inducidas en el tubo de metal.

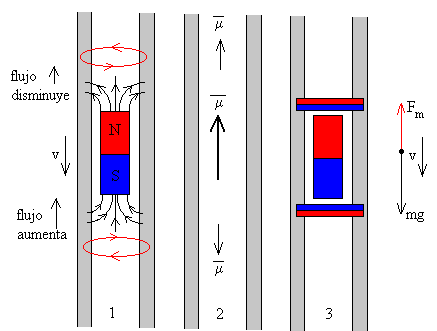
1. Durante el descenso del imán, el flujo del campo magnético se incrementa en la región próxima al polo Sur del imán. Se origina en el tubo una corriente inducida que se opone al incremento de flujo, en el sentido indicado en la parte (1) de la figura.
2. El flujo del campo magnético disminuye en la región próxima al polo Norte, se origina en el tubo una corriente inducida que se opone a la disminución del flujo, en el sentido indicado en la parte (1) de la figura

El momento magnético del imán y el de las corrientes inducidas está representado en la parte (2) de la figura.

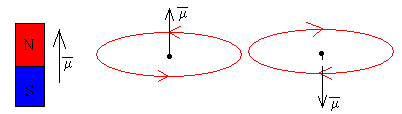
En la figura (3), mostramos la equivalencia entre corrientes (espiras o solenoides) e imanes, de modo que la corriente inducida por delante del polo Norte equivale a un imán de polaridad opuesta, por lo que se repelen. Sin embargo, la corriente inducida por detrás del imán tiene la misma polaridad por lo que se atraen.

El imán que desciende por el tubo metálico es repelido por delante y atraído por detrás. Esta es la explicación cualitativa de la fuerza de frenado en términos de la ley de Lenz.

Descripción cuantitativa

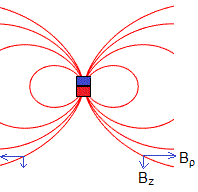
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{({\rho }^2+z^2)}^{5/2}}\hfill \\ B_z=\frac{{\mu }_0\mu }{4\pi }\left\{\frac{3z^2}{{({\rho }^2+z^2)}^{5/2}}-\frac{1}{{({\rho }^2+z^2)}^{3/2}}\right\}\hfill \end{array}}$

El flujo del campo producido por el imán a través de una espira de radio a es.

${\displaystyle \Phi =\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=\underset{S}{{\displaystyle \int }}{B}_z·dS}$

El flujo depende solamente de la componente B_z del campo magnético

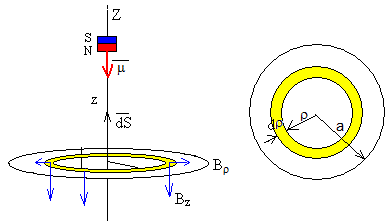
El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

${\displaystyle \begin{array}{l}\Phi =-{\displaystyle \underset{0}{\overset{a}{\int }}\frac{{\mu }_0·\mu }{4\pi }\left(\frac{3z^2}{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-\frac{1}{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}\right)2\pi \rho ·d\rho }\\ \Phi =-\frac{{\mu }_0·\mu }{4}\left(3z^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)=-\frac{{\mu }_0\mu ·a^2}{2{\left(\sqrt{a^2+z^2}\right)}^3}\end{array}}$

Aplicando la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-\frac{d\Phi }{dz}\frac{dz}{dt}=-\frac{d\Phi }{dz}(-v)=\frac{3{\mu }_0\mu a^2}{2}\frac{zv}{{\left(a^2+z^2\right)}^{5/2}}}$

Fuerza que ejerce el tubo sobre el imán

Consideremos una porción de tubo de radio medio a espesor e y altura dz, tal como se muestra en la figura. El espesor es mucho menor que el radio, e<<a

Calculamos la intensidad di de la corriente que circula por esta espira

Sea σ la conductividad del material del que está hecho el tubo, y dA=e·dz el área de la sección trasversal del anillo de longitud 2πa. La resistencia del anillo es

${\displaystyle \frac{1}{\sigma }\frac{2\pi a}{e·dz}}$

Ley de Ohm para este anillo se escribe

${\displaystyle \begin{array}{l}{V}_{\epsilon }=di\frac{1}{\sigma }\frac{2\pi a}{e·dz}\\ di=\frac{V_{\epsilon }\sigma }{2\pi a}e·dz\end{array}}$

La fuerza que ejerce el campo magnético producido por el imán sobre la corriente inducida di en el anillo es

${\displaystyle \overrightarrow{dF}=di({\widehat{u}}_t\times \overrightarrow{B})(2\pi a)}$

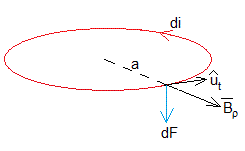
La componente B_ρ del campo magnético ejerce una fuerza a lo largo del eje Z y la componente B_z ejerce una fuerza a lo largo de la dirección radial que no tiene efecto alguno sobre un tubo rígido. El módulo de la fuerza a lo largo del eje Z es

${\displaystyle \begin{array}{l}dF=\left(2\pi a\right)B_{\rho }di=\left(2\pi a\right)\frac{{\mu }_0\mu }{4\pi }\frac{3az}{{\left(\sqrt{z^2+a^2}\right)}^5}di\\ =\frac{9{\mu }_0^2{\mu }^2}{8\pi }\frac{\sigma ev{a}^3{z}^2}{{(z^2+a^2)}^5}dz\end{array}}$

Aplicando la tercera ley de Newton, esta es la fuerza que el anillo de corriente ejerce sobre el imán. Suponiendo un tubo muy largo, la fuerza total se obtiene integrando

${\displaystyle F=\frac{9{\mu }_0^2{\mu }^2}{8\pi }\sigma ev{a}^3{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{z^2}{{(z^2+a^2)}^5}dz}}$

Haciendo el cambio de variable z=au

${\displaystyle F=\left(\frac{9{\mu }_0^2{\mu }^2}{8\pi }\frac{\sigma e}{a^4}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{u^2}{{(u^2+1)}^5}du}\right)v}$

Utilizamos MATLAB para calcular una integral, que se resuelve haciendo el cambio u=tanx

> syms u;
>> int('u^2/(u^2+1)^5',u,-inf,inf)
ans =(5*pi)/128

${\displaystyle F=\left(\frac{45{\mu }_0^2{\mu }^2}{1024}\frac{\sigma e}{a^4}\right)v}$

Ecuación del movimiento del imán

La fuerza que se opone a la caída del imán es proporcional a la velocidad y de sentido contrario al movimiento.

La ecuación del movimiento del imán es

${\displaystyle m\frac{dv}{dt}=mg-kv}$

Integramos con las condiciones iniciales siguientes: en el instante t=0, la velocidad del imán es v=0

${\displaystyle v=\frac{mg}{k}\left(1-\exp \left(-\frac{k}{m}t\right)\right)}$

La velocidad v va creciendo hasta que alcanza un valor límite constante v_l=mg/k

Integramos de nuevo, para obtuner la posición del imán en función del tiempo, sabiendo que en el instante t=0, parte del origen, z=0

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{mg}{k}\left(1-\exp \left(-\frac{k}{m}t\right)\right)\\ x=\frac{mg}{k}{\displaystyle \underset{0}{\overset{t}{\int }}\left(1-\exp \left(-\frac{k}{m}t\right)\right)dt=}\frac{mg}{k}\left(t-\frac{m}{k}\left(1-\exp \left(-\frac{k}{m}t\right)\right)\right)\end{array}}$

Representamos la velocidad v y la posición z del imán en función del tiempo t para los siguientes valores de los parámetros, tomados del artículo mencionado en las referencias:

• Masa del imán, m= 3 g
• Momento magnético del imán, μ·μ₀=4π·10^-8 T m³
• Radio interior del tubo, a=9.5 mm
• Espesor del tubo, e=1.24 mm
• Conductividad del tubo de cobre, σ=5.92·10⁷ Ω^-1m^-1

m=3/1000; %masa del imán
mu=4.7e-8; %momento magnético del imán
a=9.5/1000; %radio interior del tubo
e=1.24/1000; %espesor
sigma=5.92e7; %conductividad ohm^-1m^-1

k=45*(4*pi*mu)^2*sigma*e/(1024*a^4);
v=@(t) (m*9.8/k)*(1-exp(-k*t/m));
z=@(t) (m*9.8/k)*(t-m*(1-exp(-k*t/m))/k);

subplot(2,1,1)
fplot(v,[0,0.2])
grid on
xlabel('t')
ylabel('v')
title('Caída de un imán en un tubo vertical')

subplot(2,1,2)
fplot(z,[0,0.2])
grid on
xlabel('t')
ylabel('z')

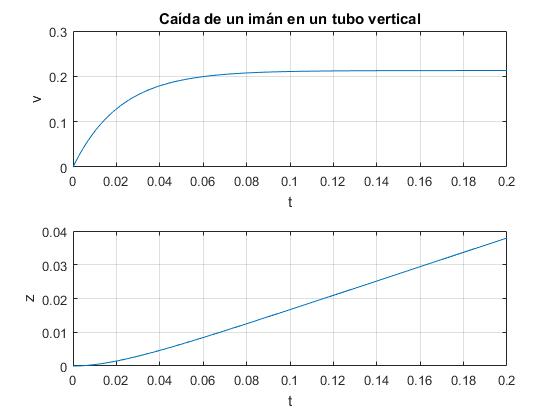
El imán alcanza en muy poco tiempo la velocidad límite constante

Fuerza que ejerce el tubo sobre el imán

Volvemos a calcular la fuerza que ejerce el tubo sobre el imán, suponiendo que el tubo tiene un radio interior a y exterior b.

Calculamos el flujo y la fem para una espira de radio r, donde a≤r≤b

${\displaystyle V_{\epsilon }=\frac{3{\mu }_0\mu r^2}{2}\frac{zv}{{(r^2+z^2)}^{5/2}}}$

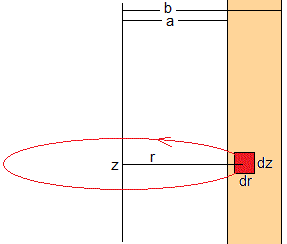
Calculamos la intensidad di de la corriente que circula por esta espira de radio r y sección dA=dr·dz. La resistencia es

${\displaystyle \frac{1}{\sigma }\frac{2\pi r}{dA}}$

Ley de Ohm para esta espira se escribe

${\displaystyle \begin{array}{l}{V}_{\epsilon }=di\frac{1}{\sigma }\frac{2\pi r}{dA}\hfill \\ di=\frac{V_{\epsilon }\sigma }{2\pi r}dA\hfill \end{array}}$

La fuerza que ejerce el campo magnético producido por el imán sobre la corriente inducida di en la espira es

${\displaystyle \begin{array}{l}\overrightarrow{dF}=di({\widehat{u}}_t\times \overrightarrow{B})(2\pi r)\\ dF=(2\pi r)B_{\rho }di=(2\pi r)\frac{{\mu }_0\mu }{4\pi }\frac{3rz}{{\left(z^2+r^2\right)}^{5/2}}di=\frac{9{\mu }_0^2{\mu }^2}{8\pi }\frac{\sigma v{r}^3{z}^2}{{\left(z^2+r^2\right)}^5}dr·dz\end{array}}$

Suponiendo un tubo muy largo, la fuerza total se obtiene integrando

${\displaystyle F=\frac{9{\mu }_0^2{\mu }^2}{8\pi }\sigma v{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{a}{\overset{b}{\int }}\frac{r^3{z}^2}{{\left(z^2+r^2\right)}^5}dz·dr}}}$

Integramos, primero, respecto de z, haciendo el cambio de variable

${\displaystyle \begin{array}{l}z=r\tan \theta ,dz=\frac{r}{{\cos }^2\theta }d\theta \\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{r^3{z}^2}{{\left(z^2+r^2\right)}^5}dz=\frac{1}{r^4}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\sin }^2\theta {\cos }^6\theta ·d\theta }=\frac{1}{r^4}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left({\cos }^6\theta -{\cos }^8\theta \right)·d\theta }}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n}\theta ·d\theta =\{\begin{array}{l}u={\cos }^{2n-1}\theta ,du=-\left(2n-1\right){\cos }^{2n-2}\theta \sin \theta ·d\theta \\ dv=\cos \theta ·d\theta ,v=\sin \theta \end{array}}\\ ={\sin \theta ·{\cos }^{2n-1}\theta |}_{-\pi /2}^{\pi /2}+\left(2n-1\right){\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n-2}\theta {\sin }^2\theta ·d\theta }=\\ \left(2n-1\right){\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n-2}\theta \left(1-{\cos }^2\theta \right)·d\theta }=\left(2n-1\right){\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n-2}\theta ·d\theta }-\left(2n-1\right){\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n}\theta ·d\theta }\\ 2n{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n}\theta ·d\theta =\left(2n-1\right){\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{2n-2}\theta ·d\theta }}\end{array}}$

El resultado de la integral respecto de z es

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^6\theta ·d\theta =\frac{5}{6}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^4\theta ·d\theta }}=\frac{5}{6}\frac{3}{4}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^2\theta ·d\theta =}\frac{5}{6}\frac{3}{4}\frac{\pi }{2}=\frac{5}{16}\pi \\ {\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^8\theta ·d\theta =\frac{7}{8}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^6\theta ·d\theta }}=\frac{7}{8}\frac{5}{16}\pi =\frac{35}{128}\pi \\ \frac{1}{r^4}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left({\cos }^6\theta -{\cos }^8\theta \right)·d\theta }=\frac{1}{r^4}\left(\frac{5}{16}\pi -\frac{35}{128}\pi \right)=\frac{5}{128}\pi \frac{1}{r^4}\end{array}}$

Ahora, integramos respecto de r entre a y b

${\displaystyle F=\frac{9{\mu }_0^2{\mu }^2}{8\pi }\sigma v{\displaystyle \underset{a}{\overset{b}{\int }}\frac{5}{128}\pi \frac{1}{r^4}dr}=\frac{45{\mu }_0^2{\mu }^2}{1024}\sigma v\frac{1}{-3}\left(\frac{1}{b^3}-\frac{1}{a^3}\right)=\frac{15{\mu }_0^2{\mu }^2}{1024}\sigma v\left(\frac{1}{a^3}-\frac{1}{b^3}\right)}$

El espesor e del tubo es, b=a+e. Supondremos que e<<a

${\displaystyle F=\frac{15{\mu }_0^2{\mu }^2}{1024}\sigma v\left(\frac{1}{a^3}-\frac{1}{a^3{\left(1+\frac{e}{a}\right)}^3}\right)\approx \frac{15{\mu }_0^2{\mu }^2}{1024}\sigma v\frac{1}{a^3}\left(1-\left(1-3\frac{e}{a}\right)\right)=\left(\frac{45{\mu }_0^2{\mu }^2}{1024}\sigma \frac{e}{a^4}\right)v}$

>> syms x;
>> taylor((1+x)^-3,x)
ans =- 21*x^5 + 15*x^4 - 10*x^3 + 6*x^2 - 3*x + 1

Obtenemos el mismo resultado

Referencias

G Donoso, C L Ladera, P Martín. Magnet fall inside a conductive pipe: motion and the role of the pipe wall thickness. Eur. J. Phys. 30 (2009) 855-869

Sanjoy Kumar Pal, Soumen Sarkar, Pradipta Panchadhyayee. Determination of the magnetic moment of a magnet by letting it fall through a conducting pipe. Phys. Educ. 59 (2024) 015022