El campo magnético $\overrightarrow{B}$ es constante y es perpendicular al plano determinado por las guías y la varilla. El flujo del campo magnético a través del circuito de forma rectangular ABCD señalado en la figura es

${\displaystyle \Phi =\overrightarrow{B}\cdot \overrightarrow{S}=Bax}$

donde a·x es el área del rectángulo ABCD.

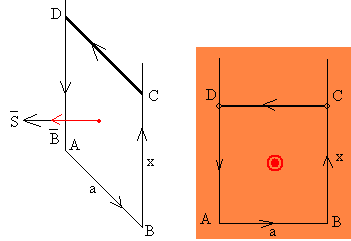
Al moverse la varilla CD la dimensión x del rectángulo disminuye. De acuerdo a la ley de Faraday, la fem inducida es

${\displaystyle V_E=-\frac{d\Phi }{dt}=-Ba\frac{dx}{dt}=Bav}$

Como x decrece con el tiempo su derivada dx/dt=v<0

Sentido de la corriente inducida

Si el campo magnético apunta hacia el lector, al disminuir el área S, disminuye el flujo Φ, el sentido de la corriente inducida es el contrario a las agujas del reloj.

Si la resistencia del circuito es R, la intensidad de la corriente inducida es i=V_E/R=vBa/R.

Resistencia de la varilla

En esta experiencia vamos a suponer que las guías son superconductoras o bien, que su resistencia es despreciable frente a la de la varilla. La varilla tiene una sección fija de 1 mm² pero su longitud a puede se puede modificarse dentro de ciertos límites.

Los materiales disponibles para fabricar la varilla son

La masa de la varilla se obtiene multiplicando la densidad por el volumen de un cilindro de sección S y longitud a. La resistencia se calcula mediante la siguiente fórmula: se multiplica la resistividad ρ por longitud L=a y se divide por la sección normal S

${\displaystyle R=\rho \frac{L}{S}}$

Movimiento de la varilla

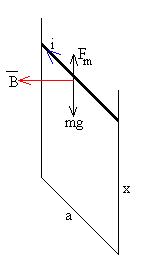
Como vemos en la figura, sobre la varilla actúan dos fuerzas, el peso mg y la fuerza F_m que ejerce el campo magnético sobre la corriente inducida i. Esta fuerza se opone siempre al movimiento de la varilla, como podremos comprobar.

Cuando circula por la varilla CD una corriente i, el campo magnético B ejerce una fuerza

${\displaystyle \overrightarrow{F_m}=i({\widehat{u}}_t\times \overrightarrow{B})L}$

El vector unitario ${\widehat{u}}_t$ que señala el sentido de la corriente y el campo $\overrightarrow{B}$ son mutuamente perpendiculares, la longitud del conductor es a.

El módulo de la fuerza magnética es

F_m=iBa=vB²a²/R

Su sentido es el indicado en la figura (hacia arriba, contrario al peso)

La ecuación del movimiento de la varilla es

${\displaystyle m\frac{dv}{dt}=mg-F_m}$

la fuerza magnética es proporcional a la intensidad de la corriente inducida y por tanto, a la velocidad de la varilla.

${\displaystyle m\frac{dv}{dt}=mg-\frac{B^2{a}^2}{R}v}$

Esta es una ecuación similar a la que describe el movimiento de una esfera que cae en el seno de un fluido viscoso, si se desprecia el empuje.

Integrando obtenemos la expresión de la velocidad en función del tiempo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{g-kv}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}k=\frac{B^2{a}^2}{mR}\\ v=\frac{g}{k}\left(1-\exp (-kt)\right)\end{array}}$

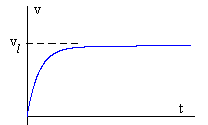
La velocidad aumenta desde cero hasta un valor límite constante

${\displaystyle v_l=\frac{g}{k}=\frac{mgR}{B^2{a}^2}}$

Poniendo la masa m igual al producto de la densidad por el volumen de la varilla, y la resistencia R igual al producto de la resistividad por la longitud de la varilla dividido su sección, comprobamos que el valor de la velocidad máxima no depende de la longitud a ni de la sección S de la varilla.

La fórmula de la velocidad se podría haber obtenido sin necesidad de integrar la ecuación del movimiento. La fuerza magnética F_m va creciendo desde cero, hasta que su valor se hace igual al peso, mg. En ese momento, la fuerza neta sobre la varilla es cero y velocidad de la varilla se hace constante.

${\displaystyle mg=\frac{B^2{a}^2}{R}{v}_l}$

Si la velocidad crece hasta alcanzar un valor límite v_l, la intensidad de la corriente inducida crece hasta alcanzar un valor límite i_l.

${\displaystyle i=\frac{Ba}{R}v{i}_l=\frac{mg}{Ba}}$

y es independiente del valor de la resistencia R del circuito.

Una vez obtenida por integración la variación de la velocidad de la varilla con el tiempo, una segunda integración nos permite determinar la altura de la varilla con el tiempo, sabiendo que en el instante inicial parte de la altura h. La ecuación es similar a la que se obtiene cuando se estudia el movimiento vertical de una esfera en el seno de un fluido.

Actividades

Se introduce

• El campo magnético (en gauss), que puede ser un número positivo (el campo magnético apunta hacia el lector), o negativo el campo magnético apunta hacia dentro, de sentido contrario al anterior.
• La longitud de la varilla (en cm), un número menor que 10.
• La sección de la varilla se ha fijado en 1.0 mm².
• Finalmente, elegimos el material del que está hecho la varilla: aluminio, cobre, hierro, plomo, wolframio.

Se pulsa el botón titulado Nuevo.

La varilla empieza a caer desde una altura inicial de 100 cm.

Sobre la varilla se dibuja los siguientes vectores:

• El peso mg, flecha vertical hacia abajo de color negro
• El campo magnético B, flecha horizontal de color azul, apuntando hacia adentro (color azul claro) o hacia afuera (color rosa) de la página.
• El sentido de la corriente inducida, flecha de color rojo a lo largo de la varilla o el sentido del movimiento de los puntos de color rojo a lo largo de la espira, que representan la corriente inducida.
• La fuerza magnética, F_m, flecha de color negro vertical apuntando hacia arriba.

En la parte derecha, se representa, la velocidad de la varilla en función del tiempo

Ejemplo

Sea una varilla de 8 cm de longitud y 1 mm² de sección, que se mueve verticalmente en un campo magnético uniforme de 300 gauss, que apunta hacia el lector. Si la varilla está hecha de aluminio, determinar la velocidad límite que alcanza la varilla y la corriente inducida límite.

• La masa m de la varilla es igual al producto de la densidad d por el volumen de la varilla de longitud a y sección S, m=d·S·a
• Su resistencia R es el producto de la resistividad ρ por la longitud de la varilla a, dividido la sección S, R=ρ·a/S

${\displaystyle \begin{array}{l}{v}_l=\frac{mgR}{B^2{a}^2}=\frac{dg\rho }{B^2}=\frac{2700·9.8·2.8·{10}^{-8}}{{\left(300·{10}^{-4}\right)}^2}=0.82\text{m/s}\\ i_l=\frac{mg}{Ba}=\frac{dgS}{Ba}=\frac{2700·9.8·1.0·{10}^{-6}}{300·{10}^{-4}}=0.88\text{A}\end{array}}$

Si elegimos otros materiales como el hierro o el plomo, la varilla no alcanza la velocidad límite constante, si la intensidad del campo magnético es pequeña.

Calculamos la velocidad y la intensidad en el instante t=0.1 s

${\displaystyle \begin{array}{l}k=\frac{B^2{a}^2}{mR}=\frac{B^2}{d\rho }=\frac{{\left(300·{10}^{-4}\right)}^2}{2700·2.8·{10}^{-8}}=11.90{\text{s}}^{\text{-1}}\\ v=\frac{g}{k}\left(1-\exp (-kt)\right)v=\frac{9.8}{11.90}\left(1-\exp (-11.90·0.1)\right)=0.57\text{m/s}\\ i=\frac{Ba}{R}v=\frac{BvS}{\rho }=\frac{300·{10}^{-4}·0.57·1.0·{10}^{-6}}{2.8·{10}^{-8}}=0.61\text{A}\end{array}}$

Anillo que cae en una campo magnético que aumenta con la altura

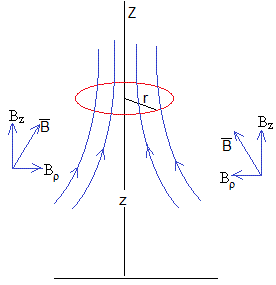
Un anillo de masa m, radio r y resistencia R, cae desde cierta altura en una región donde hay un campo magnético vertical que aumenta con la altura B_z=B₀(1+kz). Vamos a calcular la velocidad final constante del anillo, suponiendo que su plano se mantiene perpendicular al eje Z.

El campo magnético tiene simetría cilíndrica alrededor del eje Z, las componentes B_z y B_ρ están relacionadas por la ley de Gauss del campo magnético

${\displaystyle {\displaystyle \oint \overrightarrow{B}·\overrightarrow{dS}=0}}$

Consideremos la superficie cilíndrica de radio ρ y altura dz, el flujo total del campo magnético a través de la superficie cerrada es nulo.

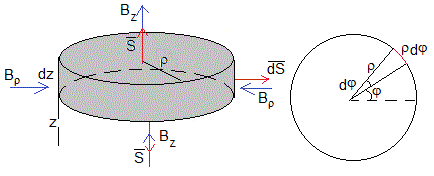
• Flujo a través de la base superior, $\overrightarrow{B}·\overrightarrow{S}=B_z\left(z+dz\right)\left(\pi {\rho }^2\right)\cos 0=\pi {\rho }^2·B_z\left(z+dz\right)$

• Flujo a través de la base inferior, $\overrightarrow{B}·\overrightarrow{S}=B_z\left(z\right)\left(\pi {\rho }^2\right)\cos 180=-\pi {\rho }^2·B_z\left(z\right)$

• Flujo a través de la superficie lateral, ${\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}={\displaystyle \underset{0}{\overset{2\pi }{\int }}{B}_{\rho }\left(\rho ·d\phi ·dz\right)\cos 180}=-B_{\rho }\left(2\pi \rho \right)dz$

La suma de las tres contribuciones al fujo es cero

${\displaystyle \begin{array}{l}\pi {\rho }^2\left(B_z\left(z+dz\right)-B_z\left(z\right)\right)-B_{\rho }\left(2\pi \rho \right)dz=0\\ \rho \frac{d{B}_z}{dz}dz-2B_{\rho }dz=0\\ B_{\rho }=\frac{\rho }{2}\frac{d{B}_z}{dz}\end{array}}$

El flujo a través del anillo de radio r y resistencia R, va disminuyendo ya que el campo aumenta con la altura z. Se genera una corriente inducida en el sentido contrario a las agujas del reloj.

${\displaystyle \begin{array}{l}\Phi =\overrightarrow{B}·\overrightarrow{S}=B_z\pi r^2\cos 0=B_0\left(1+kz\right)\pi r^2\\ V_{\epsilon }=-\frac{d\Phi }{dt}=-B_{0}k\pi r^2\frac{dz}{dt}=-\pi B_{0}k{r}^2(-v)\\ i=\frac{\pi B_{0}k{r}^2}{R}v\end{array}}$

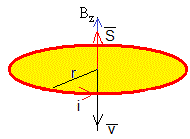
Alternativamente, calculamos la fem mediante una fórmula adecuada cuando el conductor se mueve en el seno de un campo magnético

${\displaystyle \begin{array}{l}{V}_{\epsilon }={{\displaystyle \oint (\overrightarrow{v}\times \overrightarrow{B})·\overrightarrow{dl}}}^{\text{}}{}^{\text{}}={\displaystyle \oint \left(v{B}_{\rho }\sin 90\right)dl·\cos 0}=v{B}_{\rho }2\pi r\\ i=\frac{V_{\epsilon }}{R}=\frac{v{B}_{\rho }2\pi r}{R}\end{array}}$

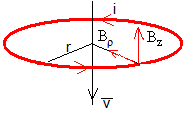
Calculamos ahora, la fuerza que ejerce el campo magnético sobre la corriente inducida

${\displaystyle \begin{array}{l}\overrightarrow{F}=i({\widehat{u}}_t\times \overrightarrow{B})l\\ F_z=i{B}_{\rho }\left(2\pi r\right)=\frac{B_{\rho }^2{\left(2\pi r\right)}^2}{R}v\end{array}}$

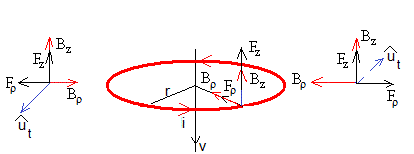
La fuerza sobre el anillo, F_z es proporcional a la velocidad v y de sentido contrario. La fuerza F_ρ no tiene efecto sobre el movimiento del anillo

Teniendo en cuenta la relación entre las dos componentes del campo magnético

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{r}{2}\frac{d{B}_z}{dz}=\frac{r}{2}{B}_{0}k\\ F_z={\pi }^2\frac{k^2{B}_0^2{r}^4}{R}v\end{array}}$

Cuando se alcanza la velocidad límite constante, v_∞, el peso mg se equilibra con la fuerza F_z

${\displaystyle \begin{array}{l}mg={\pi }^2\frac{k^2{B}_0^2{r}^4}{R}{v}_{\infty }\\ v_{\infty }=\frac{mgR}{{\pi }^2{k}^2{B}_0^2{r}^4}\end{array}}$

Energías

• La energía por unidad de tiempo disipada en la resistencia R del anillo es i²R

${\displaystyle i^{2}R={\left(\frac{\pi B_{0}k{r}^2}{R}v\right)}^{2}R=\frac{{\pi }^2{B}_0^2{k}^2{r}^4}{R}{v}^2}$

• La energía potencial gravitatoria del anillo es mgz, en la unidad de tiempo disminuye

${\displaystyle mg\frac{dz}{dt}=-mgv}$

En el estado estacionario, cuando se alcanza la velocidad límite constante, v_∞, la energía potencial gravitatoria se transforma en calor en la resistencia R del anillo

${\displaystyle \begin{array}{l}\frac{{\pi }^2{B}_0^2{k}^2{r}^4}{R}{v}_{\infty }^2=mg{v}_{\infty }\\ v_{\infty }=\frac{mgR}{{\pi }^2{B}_0^2{k}^2{r}^4}\end{array}}$

Obtenemos el mismo resultado

Referencias

Physics Challenges for Teachers and Students. Ring, Ring, Ring...(A4). The Physics Teacher. Vol. 43, (2005) pp. 250