Oscilador mecánico

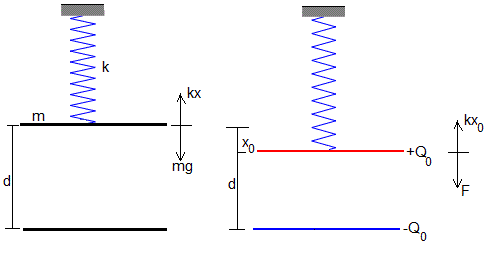
Sea un condensador de placas planas y paralelas de área S cuya placa superior de masa m, cuelga de un muelle elástico de constante k. La placa inferior está fija. Inicialmente, la separación entre las placas es d. El condensador se carga con Q₀ y su separación disminuye a d-x₀ debido a la fuerza de atracción F entre las placas

La energía del condensador cargado es

${\displaystyle U=\frac{1}{2}\frac{Q^2}{C},C=\frac{{\epsilon }_{0}S}{d-x}}$

La fuerza de atracción entre las placas

${\displaystyle F=-\frac{dU}{dx}=\frac{1}{2}\frac{Q^2}{{\epsilon }_{0}S}}$

En el equilibrio, F=kx₀

${\displaystyle x_0=\frac{1}{2k}\frac{Q_0^2}{{\epsilon }_{0}S}}$

Oscilador electromagnético

La ecuación de un circuito LC es

${\displaystyle \begin{array}{l}{V}_L+\frac{Q}{C}=0\hfill \\ -L\frac{di}{dt}+\frac{Q}{C}=\mathrm{0,}i=-\frac{dQ}{dt}\hfill \\ \frac{d^{2}Q}{d{t}^2}+\frac{1}{LC}Q=0\hfill \end{array}}$

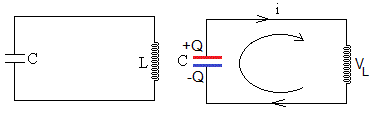
La corriente i extrae carga de la placa positiva por lo que i=-dQ/dt

Osciladores acoplados

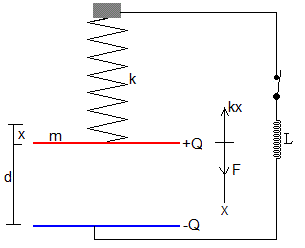
En el instante t cuando la carga del condensador es Q y la separación entre las placas es d-x, la ecuación del movimiento de la placa superior de masa m es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-kx+\frac{1}{2}\frac{Q^2}{{\epsilon }_{0}S}}$

Tenemos que resolver un sistema de dos ecuaciones diferenciales, una para el oscilador electromagnético y otra, para el oscilador mecánico

Definimos las variables adimensionales

${\displaystyle z=\frac{x}{d},q=\frac{Q}{Q_0},T=\sqrt{\frac{k}{m}}t}$

La ecuación del movimiento se expresa

${\displaystyle \begin{array}{l}d\frac{k}{m}\frac{d^{2}z}{d{T}^2}=-\frac{k}{m}z·d+\frac{Q_0^2}{2{\epsilon }_{0}Sm}{q}^2\\ \frac{d^{2}z}{d{T}^2}=-z+\frac{Q_0^2}{2{\epsilon }_{0}Sm\frac{k}{m}d}{q}^2\\ \frac{d^{2}z}{d{T}^2}=-z+z_0{q}^2,z_0=\frac{x_0}{d}=\frac{1}{2}\frac{Q_0^2}{{\epsilon }_{0}Skd}\end{array}}$

La ecuación del circuito LC

${\displaystyle \begin{array}{l}{Q}_0\frac{k}{m}\frac{d^{2}q}{d{T}^2}+\frac{Q_0}{L\frac{{\epsilon }_{0}S}{d-zd}}q=0\\ \frac{k}{m}\frac{d^{2}q}{d{T}^2}+\frac{d}{{\epsilon }_{0}SL}\left(1-z\right)q=0\\ \frac{d^{2}q}{d{T}^2}=-{\Omega }^2\left(1-z\right)q,{\Omega }^2=\frac{\frac{d}{{\epsilon }_{0}SL}}{\frac{k}{m}}=\frac{{\omega }_E^2}{{\omega }_M^2}\end{array}}$

Se resuelve el sistema de dos ecuaciones diferenciales acopladas por el procedimiento numérico ode45 de MATLAB, con las siguientes condiciones iniciales: En el instante t=0, (T=0) .

• la carga inicial del condensador es Q₀ (q₀=1) y la corriente es nula cuando se cierra el circuito, dq/dT=0

• La posición inicial de la placa superior es x₀, (0<z₀<1), y se suelta dx/dt=0 (dz/dT=0)

Datos:

• Masa de la placa superior, m=100 g
• Constante del muelle, k=3.6 N/m
• Coeficiente de autoinducción de la bobina, L=2.95 H
• Distancia entre las placas antes de cargar el condensador, d=2 cm.
• Posición inicial de la placa superior, z₀=0.5

Dada la posición inicial z₀, estimamos la carga inicial del condensador Q₀ =0.113·10^-6 C=0.113 μC

S=200e-4; %área de la placa en m2
k=3.6; %Constante del muelle en N/m
d=2/100; %distancia entre las placas en m
z0=0.5; %posición de equilibrio;

Q0=sqrt(z0*S*k*d/(pi*18e9));
disp(Q0)

   1.1284e-07

Resolvemos el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB

S=200e-4; %área de la placa en m2
m=100/1000; %masa de la placa superior en kg
k=3.6; %Constante del muelle en N/m
L=2.95; %autoinducción de la bobina en H
d=2/100; %distancia entre las placas en m
Q0=0.1e-6; %carga inicial del condensador
Omega_2=(d*4*pi*9e9/(S*L))/(k/m);
z0=0.5; %posición inicial

fg=@(t,x)[x(2);-x(1)+z0*x(3); x(4);-Omega_2*(1-x(1))*x(3)];
[t,x]=ode45(fg,[0,14],[z0,0,1,0]);
plot(t,x(:,1))
grid on
xlabel('T')
ylabel('z');
title('Desplazamiento, z')

figure
plot(t,x(:,3))
grid on
xlabel('T')
ylabel('q');
title('Carga, q')

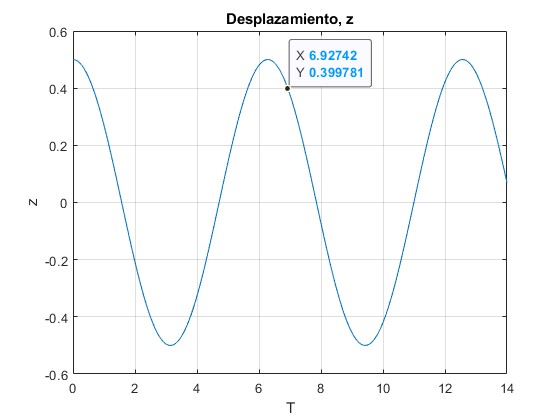
Representamos el desplazamiento z en función del tiempo T de la placa superior del condensador

Representamos la carga q del condensador en función del tiempo T

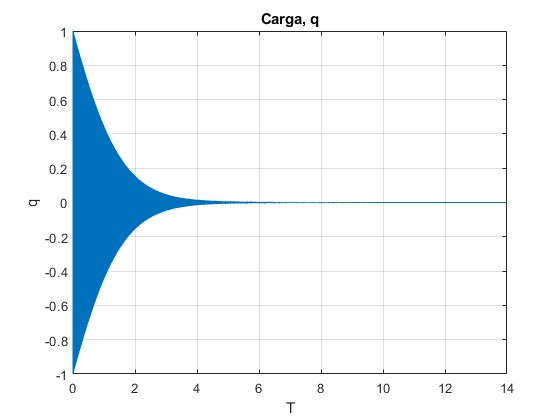
La frecuencia angular del oscilador mecánico ω_M es mucho menor que la frecuencia angular ω_E del oscilador electromagnético. Ω=32 634

>> sqrt(Omega_2)
ans =   3.2634e+04

Aproximaciones

• Carga q del condensador en un pequeño intervalo de tiempo, T₁≤T≤T₁

Las oscilaciones de la carga q son tan rápidas que podemos considerar z constante en un pequeño intervalo de tiempo. Resolvemos la ecuación diferencial del oscilador electromagnético tomando z constante

${\displaystyle \begin{array}{l}\frac{d^{2}q}{d{T}^2}+{\Omega }^2\left(1-z\right)q=0\\ q=A\cos \left(\omega T\right)+B\sin \left(\omega T\right),\omega =\Omega \sqrt{1-z}\\ \frac{dq}{dT}=\omega \left(-A\sin \left(\omega T\right)+B\cos \left(\omega T\right)\right)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales en el instante T₁

${\displaystyle \begin{array}{l}T=T_1,{\{\begin{array}{l}q=q_1\\ \frac{dq}{dT}=\frac{dq}{dT}|\end{array}}_1\\ \{\begin{array}{l}{q}_1=A\cos \left(\omega T_1\right)+B\sin \left(\omega T_1\right)\\ {\frac{dq}{dT}|}_1=\omega \left(-A\sin \left(\omega T_1\right)+B\cos \left(\omega T_1\right)\right)\end{array}\\ B=q_1\sin \left(\omega T_1\right)+\frac{1}{\omega }{\frac{dq}{dT}|}_1\cos \left(\omega T_1\right),A=q_1\cos \left(\omega T_1\right)-\frac{1}{\omega }{\frac{dq}{dT}|}_1\sin \left(\omega T_1\right)\end{array}}$

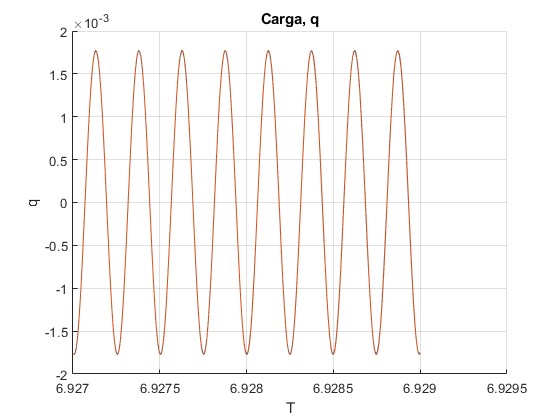
En el pequeño intervalo de tiempo 6.927≤T≤6.929, en el que z≈0.4 (véase la primera gráfica). Comparamos la solución numérica con la analítica aproximada, apreciamos que coinciden

S=200e-4; %área de la placa en m2
m=100/1000; %masa de la placa superior en kg
k=3.6; %Constante del muelle en N/m
L=2.95; %autoinducción de la bobina en H
d=2/100; %distancia entre las placas en m
Q0=0.1e-6; %carga inicial del condensador
Omega_2=(d*4*pi*9e9/(S*L))/(k/m);
z0=0.5; %posición inicial

%solución numérica
fg=@(t,x)[x(2);-x(1)+z0*x(3); x(4);-Omega_2*(1-x(1))*x(3)];
[t,x]=ode45(fg,[0,14],[z0,0,1,0]);
ind1=find(t>6.927);
ind2=find(t>6.929);
t1=t(ind1(1));
hold on
plot(t(ind1(1):ind2(1)),x(ind1(1):ind2(1),3)) 

%solución analítica aproximada
z1=x(ind1(1),1); %posición en t1 
q1=x(ind1(1),3); %carga en t1
dq1=x(ind1(1),4); %derivada dq/dt en t1
w=sqrt(Omega_2*(1-z1));
B=q1*sin(w*t1)+dq1*cos(w*t1)/w;
A=q1*cos(w*t1)-dq1*sin(w*t1)/w;
q=@(t) A*cos(w*t)+B*sin(w*t);
fplot(q,[t1,t(ind2(1))])
hold off
grid on
xlabel('T')
ylabel('q');
title('Carga, q')



• Desplazamiento z de la placa superior

La oscilación de la carga q es muy rápida, por lo que se reemplaza q² por su valor medio

${\displaystyle <{\sin }^2\left(\omega t\right)>=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\left(\omega t\right)dt=\frac{1}{2}}}$

>> syms t;
>> int(sin(t)^2,t,0,pi)/pi

La ecuación del movimiento de la placa superior se convierte en

${\displaystyle \frac{d^{2}z}{d{T}^2}+z=\frac{z_0}{2}}$

La solución de la homogénea es z_h=Acos(T)+Bsin(T). La solución particular es una constante z_p=C, introduciendo en la ecuación diferencial C=z₀/2. La solución de la ecuación diferencial es la suma

${\displaystyle \begin{array}{l}z=A\cos (T)+B\sin (T)+\frac{z_0}{2}\\ \frac{dz}{dT}-A\sin (T)+B\cos (T)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}T=\mathrm{0,}\{\begin{array}{l}z=z_0\\ \frac{dz}{dT}=0\end{array}\\ z_0=A+\frac{z_0}{2},0=B\\ z=\frac{z_0}{2}\left(1+\cos (T)\right)\end{array}}$

Se ajusta la solución numérica a la función, cuyos parámetros a y ω son desconocidos

${\displaystyle z=z_0+a\left(\cos \left(\omega T\right)-1\right)}$

para ello, utilizamos la función fminsearch de MATLAB

S=200e-4; %área de la placa en m2
m=100/1000; %masa de la placa superior en kg
k=3.6; %Constante del muelle en N/m
L=2.95; %autoinducción de la bobina en H
d=2/100; %distancia entre las placas en m
Q0=0.1e-6; %carga inicial del condensador
Omega_2=(d*4*pi*9e9/(S*L))/(k/m);
z0=0.5; %Q0^2*4*pi*9e9/(2*k*S*d);

fg=@(t,x)[x(2);-x(1)+z0*x(3); x(4);-Omega_2*(1-x(1))*x(3)];
[t,x]=ode45(fg,[0,14],[z0,0,1,0]);
hold on
plot(t,x(:,1))
%ajuste
f=@(a,t) z0+a(1)*(cos(a(2)*t)-1);      
error=@(a) sum((x(:,1)-f(a,t)).^2);
a0=[z0/2,1];  %valor inicial
af=fminsearch(error,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
hold off
grid on
xlabel('T')
ylabel('z');
title('Desplazamiento, z')

Coinciden la solución numérica y el ajuste a dicha función



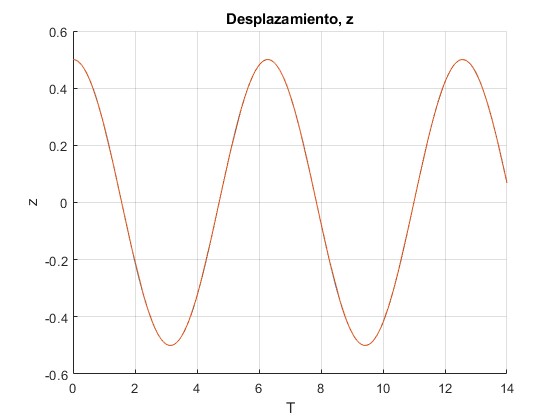
El parámetro a=1/2 y el parámetro ω=1

>> af
af =    0.5000    1.0000

Introducimos la ecuación del desplazamiento en la del circuito LC

${\displaystyle \frac{d^{2}q}{d{T}^2}=-{\Omega }^2\left(1-z_0+a\left(\cos \left(\omega T\right)-1\right)\right)q}$

Hacemos el cambio de variable τ=ωT/2

${\displaystyle \begin{array}{l}\frac{{\omega }^2}{4}\frac{d^{2}q}{d{\tau }^2}+{\Omega }^2\left(1-z_0-a\left(\cos \left(2\tau \right)-1\right)\right)q=0\\ \frac{d^{2}q}{d{\tau }^2}+\left(\alpha -2\beta \cos \left(2\tau \right)\right)q=\mathrm{0,}\{\begin{array}{l}\alpha =4\frac{{\Omega }^2}{{\omega }^2}\left(1-z_0+a\right)\\ \beta =2\frac{{\Omega }^2}{{\omega }^2}a\end{array}\end{array}}$

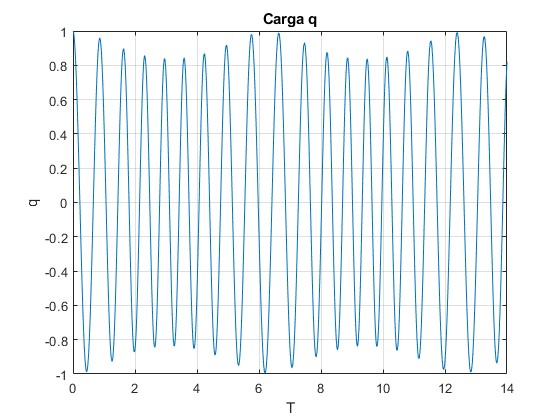
que es la ecuación de Mathieu, cuya solución analítica no está disponible, por el momento, en MATLAB.

Resolvemos esta ecuación diferencial por el procedimiento ode45 de MATLAB para los siguientes valores de los parámetros, z₀=0.5, ω=1, a=0.25, Ω=10

Las condiciones iniciales son, en el instante τ=0, q=1, dq/dτ=0

Omega=10;
a=0.25;
w=1;
z0=0.5;
alfa=4*Omega^2*(1-z0+a)/w^2;
beta=2*Omega^2*a/w^2;
fg=@(t,x)[x(2); -(alfa-2*beta*cos(2*t))*x(1)];
[t,x]=ode45(fg,[0,7],[1,0]);
plot(2*t,x(:,1))
grid on
xlabel('T')
ylabel('q');
title('Carga q')

Referencias

Carl E Mungan, Trevor C Lipscombe. Hanging a capacitor plate from a spring: a coupled mechanical–electromagnetic oscillator. Eur. J. Phys. 43 (2022) 035805